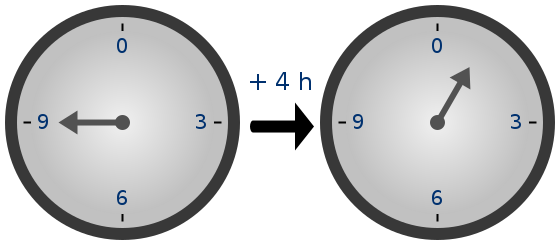
[code][/code][br][b][center]Aritmética modular[/center][/b].[br][br]En [url=https://es.wikipedia.org/wiki/Matem%C3%A1tica]matemática[/url], la [b]aritmética modular[/b] es un sistema aritmético para [url=https://es.wikipedia.org/wiki/Clase_de_equivalencia]clases de equivalencia[/url] de [url=https://es.wikipedia.org/wiki/N%C3%BAmero_entero]números enteros[/url] llamadas [b]clases de congruencia[/b]. La aritmética modular fue introducida en [url=https://es.wikipedia.org/wiki/1801]1801[/url] por [url=https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss]Carl Friedrich Gauss[/url] . Algunas veces se le llama, sugerentemente, [i]aritmética del reloj[/i], ya que los números «dan la vuelta» tras alcanzar cierto valor llamado [i][b]módulo[/b][/i].[br][br][color=#000000][b][center]Relación de congruencia.[/center][br][/b][/color]La aritmética modular puede ser construida matemáticamente mediante la [i][url=https://es.wikipedia.org/wiki/Congruencia_(teor%C3%ADa_de_n%C3%BAmeros)]relación de congruencia[/url][/i] entre enteros, que es compatible con las operaciones en el [url=https://es.wikipedia.org/wiki/Anillo_de_los_n%C3%BAmeros_enteros]anillo de enteros[/url]: suma y multiplicación. Para un determinado [url=https://es.wikipedia.org/wiki/M%C3%B3dulo_(matem%C3%A1tica)]módulo[/url] [i]n[/i], ésta se define de la siguiente manera:[br][i]a[/i] y [i]b[/i] se encuentran en la misma "clase de congruencia" módulo [i]n[/i], si ambos dejan el mismo resto si los dividimos entre [i]n[/i], o, equivalentemente, si [i]a[/i] − [i]b[/i] es un múltiplo de [i]n[/i].[br]Esta relación se puede expresar cómodamente utilizando la notación de Gauss:[br][code][/code]{\displaystyle a\equiv b\ {\pmod {n}}}[img]https://wikimedia.org/api/rest_v1/media/math/render/svg/4b21a4c5bd39316606eea0c57f2eec9f91a98276[/img]Así se tiene por ejemplo[br]{\displaystyle 63\equiv 83\ {\pmod {10}}}[img]https://wikimedia.org/api/rest_v1/media/math/render/svg/4b53fb7ee35532eae5758f952c9121c665cbc9e9[/img]ya que ambos, 63 y 83 dejan el mismo resto (3) al dividir entre 10, o, equivalentemente, 63 − 83 es un múltiplo de 10. Se lee:[br]«[i]63 es congruente con 83, módulo 10[/i]», «[i]en módulo 10, 63 y 83 son congruentes[/i]», o «[i]63 y 83 son congruentes uno con otro, módulo 10[/i]».[br]«Módulo» a veces se abrevia con la palabra «mod» al hablar, de la misma manera que como está escrito y proviene de la palabra [i]modulus[/i] del [url=https://es.wikipedia.org/wiki/Lat%C3%ADn]latín[/url], la lengua de los escritos originales de Gauss. Así, el número [i]n[/i], que en este ejemplo es 10, sería el [b]modulus[/b].[br]Otro ejemplo; cuando el módulo es 12, entonces cualesquiera dos números que divididos entre doce den el mismo resto son equivalentes (o "congruentes") uno con otro. Los números[br]..., −34, −22, −10, 14, 26,...son todos "congruentes módulo 12" unos con otros, ya que cada uno deja el mismo [url=https://es.wikipedia.org/wiki/Resto]resto[/url] (2) cuando los dividimos entre 12. La colección de todos esos números es una clase de congruencia[br][br]