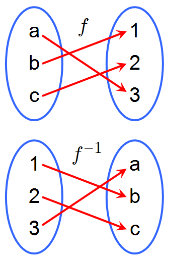
Se llama [b]función inversa o reciproca de[/b][b] [/b][i][b]f[/b][/i][b] [/b][b]a otra función[/b][b] [/b][i][b]f[sup]−1[/sup][/b][/i] que cumple que: [br][br][center][b]Si f(a) = b, entonces[/b][b] [/b][i][b]f[sup]−1[/sup][/b][/i][b](b) = a.[br][br][/b][/center]

Podemos observar que:[br]-         El dominio de [i]f[sup]−1[/sup][/i] es el recorrido de [i]f[/i].[br]-         El recorrido de [i]f[sup]−1[/sup][/i] es el dominio de [i]f[/i].[br][br]Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.[br]Si dos [b]funciones[/b] son [b]inversas[/b] su [b]composición[/b] es la [b]función identidad[/b].[br][br][center][b]([/b][i][b]f[/b][/i][b] [/b][b]o[/b][b] [/b][i][b]f[sup]−1[/sup][/b][/i][b]) (x) = ([/b][i][b]f[sup]−1[/sup][/b][/i][b] [/b][b][b]o[/b][b] [/b][i][b]f[/b][/i][b]) ([/b][i][b]x[/b][/i][b]) = x[/b][/b][/center][b][br][u][i]Cálculo de la función inversa:[/i][/u][/b][br][b]1[/b].Se escribe la ecuación de la función con x e y.[br][b]2[/b].Se despeja la variable x en función de la variable y.[br][b]3[/b].Se intercambian las variables.[br][br][i]EJEMPLO:[/i] [br][math]y=2x[/math][br]1) Cambiamos la [i][b]x[/b][/i] por la [b][i]y[/i][/b], nos queda entonces [math]x=2y[/math][br]2) Despejamos la [b][i]y[/i][/b], nos queda entonces [math]y=\frac{x}{2}[/math][br]Por tanto la función inversa de [math]y=2x[/math] es [math]y=\frac{x}{2}[/math][br]