Projectile problem - Lesson plan
General information
[list][*]Subject: Mathematics[br][/*][*]Grade: 9th grade[br][/*][*]Duration: 100 minutes[br][/*][*]ICT settings:[i] [/i]teacher computer with projector, student computers, or student phones with geogebra installed.[/*][/list]
Topics: Quadratic functions applications
[i]This lesson has as a central element the projectile's problem, meaning finding the position at any time of an object after it has been thrown in one direction at an initial speed from a certain initial position. It has enormous many practical applications: from measuring buildings to sports and even military applications (drafting weapons).[/i]
Specific objectives
[list][*][i][i]What knowledge, skills and / or attitudes will students acquire during the lesson? During the lesson, students will understand the depth and diversity of practical results from the problem of throwing an object.[/i][/i][/*][*][i][i]What new knowledge will students have at the end of the lesson? They will know the law of moving an object thrown from a certain height at a given angle and speed and the fact that it is a direct application of the second degree function.[/i][br][/i][/*][*][i][i]What will students be able to do as a result of the lesson? Students will be able to deduce the maximum stroke, maximum height, velocity and landing angle of an object tossed from a certain height when the initial speed, initial height and throw angle are known (or deduct initial velocity when knocking is known maximum). They will be able to imagine new experiments, and to ask themselves new problems related to the accelerated movement of an object in a gravitational field.f[/i][/i][/*][/list]
Operational objectives and evaluation
Obiective operaționale și evaluare[br][list][/list][br][i]Describe the operational objectives and how to evaluate the lesson.[br][list][*][i][i]What are the operational objectives that will lead to the specific objectives?[/i][/i][br][/*][/list][/i][list=1][*]To remove the parameter t (time) from the parametric motion equations to obtain the second degree equation that determines the motion trajectory. [i][br][/i][/*][*]To solve the equation obtained to deduce the maximum range.[/*][*]To calculate the coordinates of the peak of the parabola to deduce the maximum height.[/*][*]To understand the physical phenomenon by direct experimentation.[/*][*]To use the GeoGebra "Projectile Movement" application to study the motion simulation of a moving object under the influence of gravity and calculate the initial velocity (or maximum range).[/*][*]To discuss the differences between the calculated and the experimental results, thus deducting the implication of the friction force from the air, as well as some measurement errors.[/*][/list][i][list][*][i]What are the appropriate methods to assess the achievement of these operational objectives? [/i][br][/*][/list][/i][list=1][*]Active participation in the demonstration / deduction of some equations and formulas related to the projectile problem.[/*][*]Active participation in the experimental part of the lesson - placing the objects in the required position, measuring the angles and distances, throwing the projectile, shooting with the stroboscopic lamp, etc. [/*][*]Use previously prepared GeoGebra applications to observe motion simulation and calculate the requested parameters.[/*][/list][i][list][*][i]How will you evaluate how effective the lesson was? [/i][br][/*][/list][/i][list=1][*]By observing students during activities; [/*][*]By talking with students - heuristic methods;[/*][*]By checking how to solve proposed problems and the results obtained.[/*][/list]
Teaching strategies
[i]Describe the strategies and activities used in the lesson.[br][list][*][i]What teaching methods - learning, techniques and learning activities do you intend to use? de predare - învățare, tehnici și activități de învățare intenționați să folosiți?[/i] [br][/*][/list][/i][list=1][*]Experiment method, ICT-based modeling, heuristic conversation, demonstration, problem solving.[/*][*]Experimental activities with data entry on notebooks and the use of GeoGebra Simulator / Calculator, front demonstration of formulas, problem solving on notebooks.[/*][/list][list][*][i]What equipment, software, media and materials are needed to be able to use the planned instructional strategies appropriately? [/i] [br][/*][/list][list=1][*]Teacher's computer with projector, student computers, or Student phones with Geogebra installed. [/*][*]Other means: physics lab, topometric (launch angle measurement) instrument, electronic photoelectric timer (for velocity measurement), hand-held paper arrow blowing device (pvc tube), paper arrows, lamp stroboscopic, videocamera.[i][br][/i][/*][/list][list][*][i]How should resources be distributed to support learning-learning? Which phases of the lesson and for what purpose do you intend to use the new technologies? [/i][/*][/list][list=1][*]The first 50 minutes will be dedicated to experiments, data logging, Simulator / Calculator and discussion. [/*][*]The last 50 minutes will be used to demonstrate formulas and problem solving, including using Simulator / Calculator. The math formulas and problem sheet are attached at the end of the lesson plan in PDF format. They will be used according to the pupils' level of mathematical training.[/*][/list]
Experimental activity:
[list=1][*]Experimental activity will take place in the physics lab, with the collaboration of the physics teacher who will set the scene for the experiments. An electronic time gauge with photoelectric gates will be used to accurately measure the initial speed, a topometric device for measuring the angle and the initial height, and a throwing device fixed to the topometric device, for example a blow tube PVC paper arrows. To shoot the trajectory, we need to use a stroboscopic lamp, or a powerful phone with a stroboscopic lamp app. [/*][*]The Simulator / Calculator app allows two different experiments, one in which the initial speed, angle, and initial height is measured, and the maximum stroke, maximum height, time, angle, and landing speed is calculated. The second experiment measures the maximum beating and calculates the launch speed. If we only summarize the second experiment, the photoelectric gates timer is no longer needed, so it can also be set in an ordinary classroom. [/*][*]Students will be trained from the beginning on the stages and the deployment of experiments and will be grouped into 4 teams (launch, filming, measurement, recording) that will be changed between them. The activity will be guided by 2 teachers, physics and mathematics, to respect interdisciplinarity, and it will take an hour, enough for students to experiment, but to discuss, ask, learn about the many applications of this problem. [br][/*][*]Students must discover that the projectile's trajectory is parabolic, regardless of the initial parameters (excluding vertical launch and free fall), and give examples of other parabolic movements they have observed in the real world. They will watch small movies on the Internet with parabolic movements to answer the question of what they have in common and discuss gravity and gravity acceleration. Let's not forget about recording the data and then discussing the differences that occur between the calculations and the actual data. Thus, we will discuss the friction force with air and aerodynamic forms. [/*][/list]
Resourses
[i]Explain and add links to the online resources that will be used in your lesson by you and / or students.[br][/i][list][*]Projectile problem - maths formulas[i][br][/i][/*][/list][list=1][*]Launching from ground level and landing at the same level: [url=https://www.geogebra.org/m/GRG6vbBX]https://www.geogebra.org/m/GRG6vbBX[/url][/*][*]Launching from height h>0 and landing at ground level: [url=https://www.geogebra.org/m/rJrh9dCB]https://www.geogebra.org/m/rJrh9dCB[/url] [/*][/list][list][*]Projectile motion - Simulator/Calculator: [url=https://ggbm.at/j7Tt2Zb9]https://ggbm.at/j7Tt2Zb9[/url][/*][*]Parabolas similarity: [url=https://ggbm.at/vGQ4Rhup]https://ggbm.at/vGQ4Rhup[/url][/*][/list]
Integration of new technologies
[i]Describe a plan to minimize the difficulties that may come with the use of new technologies during the lesson. [br][/i][br][i]Do you or your students need specific prior knowledge to be able to use the technology appropriately within the lesson? How can you ensure the acquisition of these skills before the lesson? [br][/i]Not. They only need their attention. [br][br][i]What prior planning / programming is required to make ICT resources work properly? [br][/i]For the expected success, the activity must be timed out and all the resources secured. [br][br][i]What reserve plan do you have in case you encounter difficulties in running ICT resources? [br][/i]Classical teachings in the worst case, performing experiments without respecting precision, etc.
Projectile motion - Simulator/Calculator
Parabolas Similarity: Use the buttons Move (object), Move drawing, Zoom In and Zoom Out, to superpose all the parabolas perfectly!
Projectile motion
Input range: launch height [0,10], launch angle [0',90'], launch speed [0,15], range [0,25]
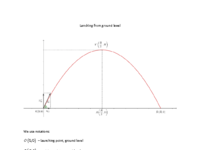
Launching from ground level
Launching from ground level and landing at the same level
Reflections after lesson
How did you implement your lesson plan?
[i]The lesson took place in a classroom equipped with a video projector, so I teached this lesson with the application in front of everyone.[br][/i][br]
Integration of new technologies into the lesson went well?
[i]Was well. The students liked it.[/i][br]
Did the pupils reach the objectives proposed in the lesson?
Being a more practical lesson, the pupils were eyes and ears, so they have brilliantly touched their goals, and even came with other ideas and simulations.[br][br]
What opinions have your students expressed about the lesson?
Students seemed interested in the new approach to the lesson. Maybe because it was something totally new. But finally GeoGebra, no matter how much it would facilitate the understanding of the concepts, can not replace the individual study that has to suffer greatly in these times. I do not expect mega-results with this program because of the laziness of the students. But those willing can move much easier with his help.
What improvements could be made to the method used to make it work better?
Maybe inserting a situation (a background image) in which the projectile is something concrete and the target is also something concrete.[br][br]
