
Minicurso 2 - Geometria Espacial
UMA REFLEXÃO SOBRE O TEMA
[justify]Através da imprescindibilidade do homem em interpretar e representar o seu meio ambiente, tanto físico quanto mental, é que as imagens, retratadas através de desenhos, foram aos poucos conceitualizadas até obterem uma definição matemática e, simultaneamente com conceitos e relações geométricas, desenvolveram a Geometria Euclidiana.[br][br]O estudo da Geometria é crucial para o desenvolvimento do pensamento espacial e o raciocínio estimulado pela visualização, carecendo empregar à intuição, à compreensão e à representação, que são competências fundamentais para interpretar o mundo em que vivemos.[/justify]
1ª ETAPA - MODELANDO UM EXEMPLO DO COTIDIANO
[justify]Foram observados objetos do cotidiano dos estudantes da Educação Básica que se enquadram na proposta da atividade, para que possam ser modelados com o auxílio do [i]software [/i]GeoGebra. A partir desta observação, nota-se que alguns objetos podem ser facilmente obtidos através da revolução de uma função[br]conhecida em torno de um eixo específico, como mostra a Figura 1.[/justify]

[justify][/justify][justify]Neste caso, o copo ilustrado na Figura 1 pode ser obtido pela revolução de um segmento de reta em torno de um eixo específico. Porém, há objetos que tornam o exercício de determinar uma função a ser rotacionada, uma tarefa complexa, como podemos observar na Figura 2.[br]Diante de tais fatos, foi elaborado um [i]applet [/i]plataforma do GeoGebra, onde é apresentado uma forma de modelar a peça de xadrez mostrada na Figura 2. Vejamos a seguir.[/justify]
2ª ETAPA - UM COMPARATIVO ENTRE SÓLIDOS E SUPERFÍCIES DE REVOLUÇÃO
[justify]A seguir, será apresentado um [i]applet[/i] desenvolvido na plataforma do software GeoGebra.[/justify]
3ª ETAPA - ATIVIDADE ORIENTADA
[justify]Nas atividades a seguir são apresentados recursos e comandos do GeoGebra para a obtenção de superfícies fechadas de revolução. Inicialmente será apresentado um roteiro de construção das mesmas.[/justify]
Atividade 3 - Roteiro de construção
[justify][b][u]Passo 1:[/u][/b] Abra um arquivo no [i]software [/i]GeoGebra e salve-o no computador. Além disso, no menu [i]Exibir[/i], habilite a [i]Janela de Visualização 3D[/i]. [br][b][u]Passo 2:[/u][/b] No campo de entrada do GeoGebra digite a função que deseja rotacionar, como por exemplo, [math]f(x)=sen(x)+x[/math]. Logo após, oculte a função [math]f[/math] da [i]Janela de Visualização [/i]1.[br][b][u]Passo 3: [/u][/b]Crie dois controles deslizantes [math]a[/math] e [math]b[/math] do tipo número, ambos com valor inicial [math]-5[/math], valor final [math]5[/math] e incremento [math]0.1[/math].[br][u][b]Passo 4:[/b][/u] Crie uma função [math]g[/math] suporte, tal que [math]a\le x\le b[/math]. Para isso, no campo de entrada do GeoGebra digite [math]g(x)=Função(f,a,b)[/math]. Nesta etapa, a aparência da construção realizada estará similar a apresentada na Figura 3. [/justify]
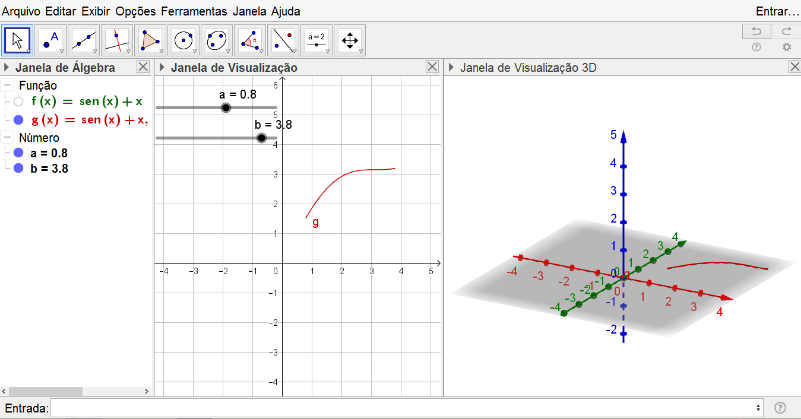
[justify][b][u]Passo 5:[/u][/b] Crie um controle deslizante [math]\alpha[/math] do tipo ângulo, com valor inicial [math]0[/math] , valor final [math]2\pi[/math] e incremento [math]5°[/math].[br][b][u]Passo 6:[/u][/b] Para realizar a revolução da curva em torno do eixo [math]Ox[/math] digite no campo de entrada o comando [math]Superfície(r,f(r)cos(θ),f(r)sen(θ),r,a,b,θ,0,α)[/math] Nesta etapa, ao alterar os valores do controle deslizante [math]\alpha[/math] já é possível visualizar a superfície de revolução, como pode ser observado na Figura 4.[/justify]
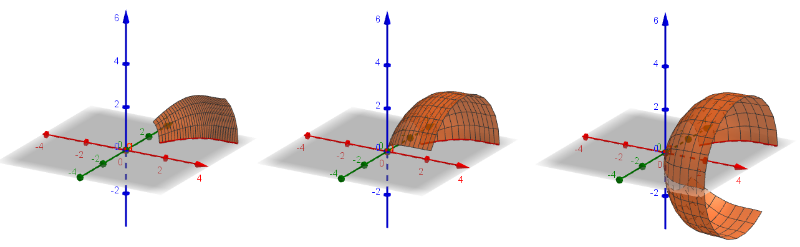
[b][u]Passo 7:[/u][/b] Para construir os círculos que limitam as superfícies fechadas inferiormente e superiormente, quando conveniente, digite os seguintes comandos no campo de entrada:[br][br]• [math]Superfície(b,cos(θ)*(t*f(b)),sen(θ)*(t*f(b)),t,0,1,θ,0,α)[/math][br]•[math]Superfície(a,cos(θ)*(t*f(a)),sen(θ)*(t*f(a)),t,0,1,θ,0,α)[/math][br][br]Após inseridos os comandos, pode-se visualizar a superfície fechada por completa, conforme apresenta a Figura 5.
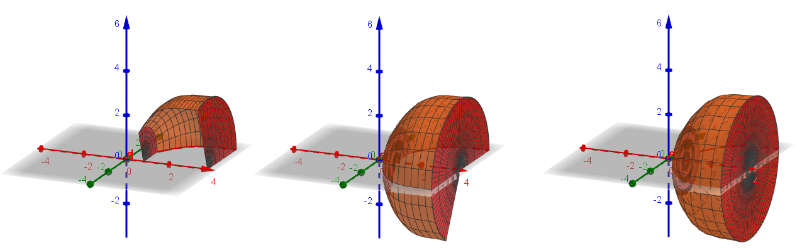
QUESTIONÁRIO DE SATISFAÇÃO - MINICURSO 1
Caro cursista, solicitamos gentilmente que responda o questionário de forma imparcial e objetiva. Para acessá-lo, [url=https://docs.google.com/forms/d/e/1FAIpQLSdnjg9_J7IIDR9ynir4YuOAR1POSI09NUbg4dPf_gN9Sb3cZg/viewform?c=0&w=1]CLIQUE AQUI[/url].