Integral Dupla
Integral Dupla
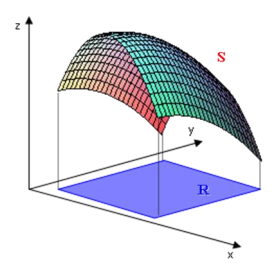
[justify]A integral dupla de uma função de duas variáveis representa o volume entre o gráfico e o plano que contém seu domínio.Segundo Anton (2014, p.1039, V.II) “[...] uma integral dupla de uma função f(x,y) é definida em uma região fechada finita R do plano xy.[...]”[/justify]
Superfície de Integração e Região de Integração

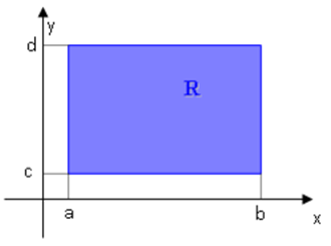
Região de integração
Volume entre a região e a superfície
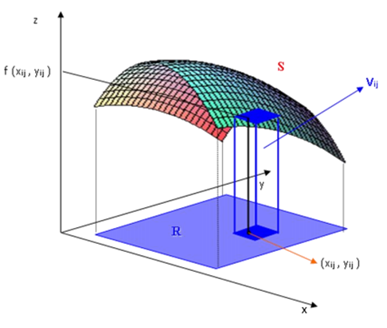
Volume por construção de prismas

[b][center]Questões:[/center][/b]
1) (Gonçalves,2007, p.242) [math]∫_{0}^{1}∫_{x^{3}}^{x^{2}}f x , y d y d x [/math]
Integral dupla 1
2) (Gonçalves,2007, p.242) [math]∫_{- 1}^{3}∫_{0}^{- x^{2}+ 2 x + 3}f x , y d y d x [/math]
Integral dupla 2
3) (Gonçalves,2007, p.242) [math]∫_{0}^{1}∫_{2 x}^{3 x}f x , y d y d x [/math]
Integral dupla 3
4) (Gonçalves, 2007, p.242) [math]∫_{0}^{2}∫_{0}^{y^{2}}f x , y d x d y [/math]
[justify]5) (Gonçalves,2007, p.242) [math]∬_{R}^{}8 - x - y d x d y [/math], onde R éa região delimitada por [math]y = x^{2}[/math] e [math]y = 4 [/math][/justify]
[justify]6) (Gonçalves,2007, p.242) [math]∬_R^{ }\left(\sqrt{x}sen\left(\sqrt{xy}\right)\right)dxdy[/math], onde R éa região delimitada por [math]y = 0 [/math] , [math]x = \frac{π}{2} [/math]e [math]y = \sqrt{x} [/math].[/justify]
[justify]7) (Gonçalves,2007, p.243) [math]∬_{R}^{}x^{2}+ y^{2} d x d y [/math], onde R éa região delimitada por [math]y = 0 [/math] , [math]x = 4 [/math]e [math]y = \sqrt{x} [/math].[/justify]
Integral dupla 7
8) (Gonçalves,2007, p.243) [math]∬_{R}^{}\frac{x^{2}}{y^{2}}d x d y [/math], onde R éa região delimitada por [math]y = x [/math] , [math]x = 2 [/math]e [math]y = \frac{1}{x} [/math].
[justify]9) (Gonçalves,2007, p.243) [math]∬_{R}^{}x + y d x d y [/math], onde R éa região delimitada por [math]y = x^{2}+ 1 [/math] , [math]y = - 1 - x^{2}[/math] , [math]x = - 1 [/math] e [math]x = 1 [/math].[/justify]
[justify]10) (Gonçalves, 2007, p.243) [math]∬_{R}^{}x d x d y [/math], onde R éa região delimitada por [math]y = - x [/math] , [math]y = 4 x [/math] e [math]y = \frac{3}{2} x + \frac{5}{2}[/math] .[/justify]
[b][center]Questões de Área com Integral Dupla:[/center][/b]
[center][math]∬_{R}^{}d x d y o u ∬_{R}^{}d y d x [/math][/center][center][/center]
[justify]1) (Gonçalves,2007, p.263) Calcular a área da região R delimitada por [math]x=y^2+1[/math] e [math]y + x = 3 [/math] .[/justify]
[justify]2) (Gonçalves,2007, p.271) Calcular a área da região R delimitada por [math]y = x^{3}[/math] , [math]x + y = 2 [/math] e [math]y = 0 [/math].[/justify]
[justify] 3) (Gonçalves,2007, p.271) Calcular a área da elipse [math] x^{2}+ 4 y^{2}- 4 x = 0 [/math].[/justify]
[justify]4) (Gonçalves,2007, p.271) Calcular a área da região delimitada por [math] y = \sqrt{4 - x^{2}} [/math], [math]y = x [/math] e [math]y = 2 x [/math].[/justify]
Integral Dupla Área 4
5) (Gonçalves,2007, p.271) Calcular a área da região delimitada por [math] y = 2 - \left( x - 2 \right)^{2} [/math] e [math]y = \frac{x^{2}}{4}[/math] .
Integral Dupla Área 5
[b][center]Questões de Volume com Integral Dupla:[/center][/b]
[justify]1) (Gonçalves,2007, p.256) Calcule o volume do sólido acima do plano [math]x y [/math] delimitado por [math]z = 4 - 2 x^{2}- 2 y^{2}[/math].[/justify]
[justify]2) (Gonçalves,2007, p.258) Calcule o volume do sólido abaixo do plano [math]x y [/math] delimitado por [math]z = x^{2}+ y^{2}- 9 [/math].[/justify]
[justify]3) (Gonçalves,2007, p.259) Calcule o volume do sólido de limitado por [math]z = 2 x^{2}+ y^{2}[/math] e [math]z = 4 - 2 x^{2}- y^{2}[/math].[/justify]
[justify]4) (Gonçalves,2007, p.261) Calcule o volume do sólido no primeiro octante, delimitado pelos cilindros [math] x^{2}+ y^{2}= 16 [/math] e [math] x^{2}+ z^{2}= 16 [/math].[/justify]
Integral Dupla Volume 4
5) (Gonçalves,2007, p.270) Calcular o volume dos sólidos delimitados pelas superfícies dadas:[br][br] [br]a) [math]y = x^{2}[/math] , [math]y = 4 [/math] , [math]z = 0 [/math] , [math]z = 4 [/math]
Integral Dupla Volume 5 a
[justify]b) [math]z = 4 x^{2}[/math] , [math]z = 0 [/math], [math]x = 0 [/math] ,[math] x = 2 [/math], [math]y = 0 [/math] e [math]y = 4 [/math].[/justify]
[justify]c) [math]z = 1 - x^{2}[/math], [math]z = 0 [/math] , [math]x + y = 4 [/math] e [math]y = 0 [/math].[/justify]
[justify]d) [math]x^{2}+ y^{2}= 1 [/math], [math]z = 0 [/math] , [math]z = x^{2}+ y^{2}[/math].[/justify]
[justify]e) [math]x^{2}+ y^{2}= 4 [/math], [math]y + z = 8 [/math] e [math]z = 0 [/math].[/justify]
[justify]f) [math]z = x^{2}+ 1 [/math] , [math]z = 0 [/math] , [math]y = 0 [/math] , [math]x = 0 [/math] , [math]x = 4 [/math] e [math]y = 5 [/math][/justify]
[justify]g) [math]z = 0 [/math] , [math]x^{2}+ y^{2}= 16 [/math] e [math]z = 10 + x [/math] .[/justify]
Integral Dupla Volume 5 g
h) [math]x^{2}+ y^{2}- 4 x - 6 y + 4 = 0 [/math] , [math]z = 0 [/math] e [math]z = 5 y [/math].
[justify]4) (Gonçalves,2007, p.261) Calcule o volume do sólido no primeiro octante, delimitado pelos cilindros [math] x^{2}+ y^{2}= 16 [/math] e [math] x^{2}+ z^{2}= 16 [/math].[/justify]