Simplex Algorithmus MAX Programm

[b][icon]/images/ggb/toolbar/mode_viewinfrontof.png[/icon][url=https://docs.google.com/spreadsheets/d/1gKxW9G7O550szURpzJLdSpxtVAfJFrt6kjItLmlyh_g/edit?usp=sharing]Grundlagen (Google Sheets - Video)[br][/url][br]X[/b] Vorgabe der [b]Strukturvariablen oder Nichtbasisvariablen x1,x2[/b] . Die [b]Basisvariablen[/b] x[sub]3[/sub] .. x[sub]7[/sub] werden im Start-Tableau als Schlupfvariablen eingetragen"[br](ggf. ändern oder ergänzen).[br][b][br]Tablo, [/b]Gleichungssystem, beginnend mit den [b]Nebenbedingungen f(x)<= b[/b]. Ungleichungen f(x) >= b ggf. "Umdrehen zu" (-1)f(x) <= -b , ergänzt durch die Basisvariablen x[sub]i[/sub] (Schlupfvariablen) zu einer Gleichung. Zum Abschluss die Zielfunktion [b]als Gleichung =0 [/b](Eintrag der Zielfunktion im Tableau wird mit (-1) multipliziert![br][br][math]\large Tablo \, := \, \left\{ 3 \; x1 + 8 \; x2 + 6 \; x3 = 800, 5 \; x1 + 2 \; x2 + x3 = 500, 2 \; x1 + 3 \; x3 = 600, x1 + x2 + x3 = 0 \right\} [/math][br][br]Aus Tablo erzeuge ich das Ausgangstableau für den 1. Simplex-Schritt, [b]Start[/b] (Zeile $5). [br]Ziel ist es durch Umformung der Start-Tableaus in der Zeile der Zielfunktion (Zeile n) ausschließlich positive Werte zu erzeugen. [br][br][b]9: A1:=Start Tableau A1 zuweisen[/b] [br]Einen Simplex-Schritt berechnen durch die Anwendung der Simplex-Schritt-Funktionen [br][table][tr][td][/td][td][color=#660000]Schritt-Berechnung[/color][br][/td][td][color=#660000]Schritt-Funktion[/color][color=#660000][/color][/td][td][color=#660000]Anwendung auf A1[/color][/td][/tr][tr][td]1:[/td][td]Pivotspalte[/td][td]PivotSpl[/td][td]kleinster Koeffizient der Zielfunktion oder Eingabe Pivot-Spalte[/td][/tr][tr][td]2:[br][/td][td]Quotient [br]b-Vektor [/td][td]Qb (b/Ai Pivotspalte)[/td][td]b-Spalte dividiert durch Koeffizienten der Pivotspalte[/td][/tr][tr][td]3:[/td][td]Pivotzeile[/td][td]PivotZle[/td][td]Zeile mit kleinstem Quotient aus Qb[/td][/tr][tr][td]4:[/td][td]Pivot-Zeilen-Element [br]aus Ai[/td][td]Pivot[/td][td]Pivot = a(PivotZle, PivotSpl)[br]dividiere Pivotzeile/ Pivot [/td][/tr][tr][td]5:[/td][td]Nächstes Tableau[/td][td]A2[/td][td]addiere Pivot zu allen anderen Zeilen und erzeuge 0en in der Pivotspalte[/td][/tr][/table][br][b]11: A2 [/b][b]Simplextabelle nach der 1. Umformung von A1[/b][br][br][i]ggf. weitere Schrittfolgen durch Kopieren von A2 nach A1 erzeugen bis die Koeffizienten der Zielfunktion (untere Zeile) positiv sind. Der Button [A2 → A1] kopiert A2 nach A1 - da das Script aber nicht im CAS arbeitet kommt es ggf. zu Rundungsfehler - zu vermeiden durch direktes Kopieren im CAS [br][color=#0000ff]A1:= [Restzeile löschen dann auf AUSGABE-Zeile von A2 klicken]! [/color][br]Über die Eingabe-Boxen Pivot-Zeile/Spalte können vom Standard-Algorithmus abweichende Angaben (z.B. für Phase 1 zum Erreichen einer Start-Basis) eingebracht werden![/i][br][br]Um beim Errechnen der Quotienten (PivotB ) keine undefinierten Werte zu erzeugen setzte ich 10^15 als Dummy-Wert bei der Minimumsuche ein.[br]Ab Zeile (18) Branch and Bound für ein ganzzahliges Optimum.[br][br][icon]/images/ggb/toolbar/mode_createlistofpoints.png[/icon]Zur JavaScript Umsetzung des [url=https://ggbm.at/fP8cnZbb]Simplex-Algorithmus[/url]

[color=#0000ff]Zielfunktion als Gleichung =0 ans Ende der Liste stellen![/color][br][br][math]Tablo:= \left\{ 3 \; x1 + 8 \; x2 + 6 \; x3 = 800, 5 \; x1 + 2 \; x2 + x3 = 500, 2 \; x1 + 3 \; x3 = 600, +x1 + x2 + x3 = 0 \right\} [/math][br][br][math]Start:= \left(\begin{array}{rrrrrrr}3&8&6&1&0&0&800\\5&2&1&0&1&0&500\\2&0&3&0&0&1&600\\-1&-1&-1&0&0&0&\textcolor{red}{0}\\\end{array}\right)[/math] [size=85]PivotSpl=1, PivotZle=2[/size], [size=85]Pivot {1, 0.4, 0.2, 0, 0.2, 0, 100}[br][/size][i]copy A2 to A1[br][math]A_1 \, := \, \left(\begin{array}{rrrrrrr}0&6.8&5.4&1&-0.6&0&500\\\textcolor{red}{1}&0.4&0.2&0&0.2&0&\textcolor{red}{100}\\0&-0.8&2.6&0&-0.4&1&400\\0&-0.6&-0.8&0&0.2&0&\textcolor{red}{100}\\\end{array}\right)[/math][/i] [size=85]PivotSpl=3, PivotZle=1[/size], [size=85]Pivot {0, 1.26, 1, 0.19, (-0.11), 0[/size], [size=85]92.59}[br][/size][i]copy A1 to A1[/i][br][math]A_2 \, := \, \left(\begin{array}{rrrrrrr}0&1.26&\textcolor{red}{1}&0.19&-0.11&0&\textcolor{red}{92.59}\\\textcolor{red}{1}&0.15&0&-0.04&0.22&0&\textcolor{red}{81.48}\\0&-4.07&0&-0.48&-0.11&1&159.26\\0&0.41&0&0.15&0.11&0&\textcolor{red}{174.07}\\\end{array}\right)[/math][br][br][math] \left\{ x1 = 81.48, x2 = 0, x3 = 92.59, max = 174.07 \right\} [/math]

SimplexAlgorithmusIntegerMAX

Beispiele

[math]Tablo \, := \, \left\{ 2 \; x1 + x2 + x_3 = 100, x1 + x2 + x_4 = 80, x1 + x_5 = 40, -3 \; x1 - 2 \; x2 = 0 \right\} [br][/math][br][br]Im Schlusstableau ist der maximale Wert für die Zielfunktion in der B-Spalte (max=180) abzulesen. [br]Die x1=20 und x2=60 Werte stehen ebenfalls in der B-Spalte in den Zeilen, in denen die x1, x2 Koeffizienten durch die Umformungen verschoben wurden.[br][br]Beispiel entnommen [url=https://sites.google.com/site/simplexverfahren/begriffe-von-a-bis-z]https://sites.google.com/site/simplexverfahren/begriffe-von-a-bis-z[/url][br]für ausführlichen Kommentierung des Algorithmus siehe dort.[br][br]maximize_lp(40*x1+20*x2,[ [br]20*x1+7*x2<=1400, 7*x1+10*x2<=1600, 8*x1+2*x2<=500, x1<=50, x2<=150][br]), nonegative_lp=true;[br][556000/151,[x2=22200/151,x1=2800/151]][br][br]Übung:[br][url=http://www.fernstudium-wiwi.de/simplextableau-umformung-fuer-dummies/]http://www.fernstudium-wiwi.de/simplextableau-umformung-fuer-dummies/[br][/url][br]Tablo:={ 20*x1+7*x2+x_3=1400, 7*x1+10*x2+x_4=1600, 8*x1+2*x2+x_5=500, x1+x_6=50, x2+x_7=150, -40*x1-20*x2=0}[br][br]Tablo:={x1+x3+x_4=8, x1+x2+x_5=7, x1+2 x2+ x_6=12, -3*x1-2*x2-2 x3=0}[br]

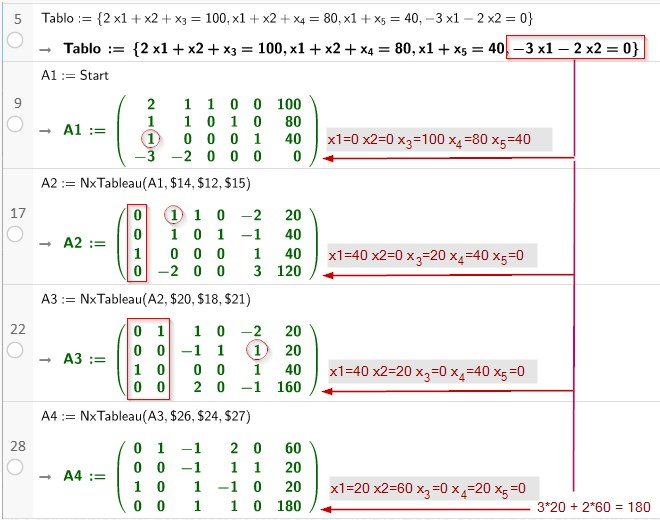
Vom Start-Tableau zum Schlußtableau

Lösungsraum mit den Ergebnissen der Simplex Tableaus

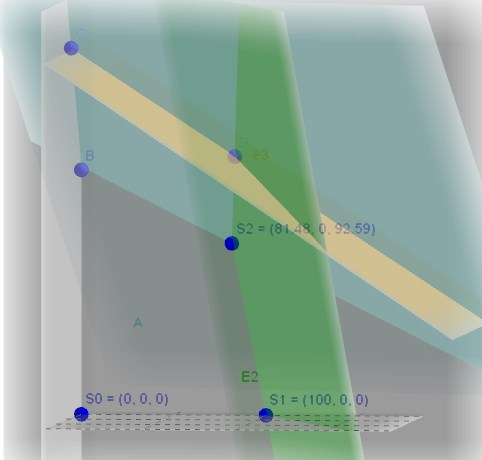
Start S0, Tableau S1 und S2

Beispiel mit TabCalc (MS Excel/Google Sheet

3 Produkte werden auf 3 Maschinen M1, M2 und M3 hergestellt. Die Belegungszeiten der Produkte auf der Maschine M1 betragen 2 Minuten für P1, 4 Minuten für P2 und 3 Minuten für P3; M1 besitzt eine freie Kapazität von 1.050 Minuten. [br]Alle Produkte belegen die Maschine M2 mit je einer Minute; die Kapazität dieser Maschine beträgt noch 450 Minuten. [br]Auf der dritten Maschine M3 kann nur P2 gefertigt werden; sie besitzt noch eine Kapazität von 150 Minuten. Die Belegungszeit von P2 auf M3 beträgt 1 Minute. [br]Der Deckungsbeitrag je Stück der 3 Produkte beträgt 50 € , 80 € bzw. 60 €.[br]a) Welche Stückzahlen sind jeweils herzustellen, damit der Gesamtdeckungsbeitrag maximal wird?[br]b) Wie groß ist der optimale Gesamtdeckungsbeitrag und wie hoch sind die freien Kapazitäten der drei Maschinen im Optimum?[br][br]Anwendung der Google Sheet [br][icon]/images/ggb/toolbar/mode_viewinfrontof.png[/icon][url=https://docs.google.com/spreadsheets/d/1gKxW9G7O550szURpzJLdSpxtVAfJFrt6kjItLmlyh_g/edit?usp=sharing]Grundlagen (Google Sheet - Video)[br][/url]

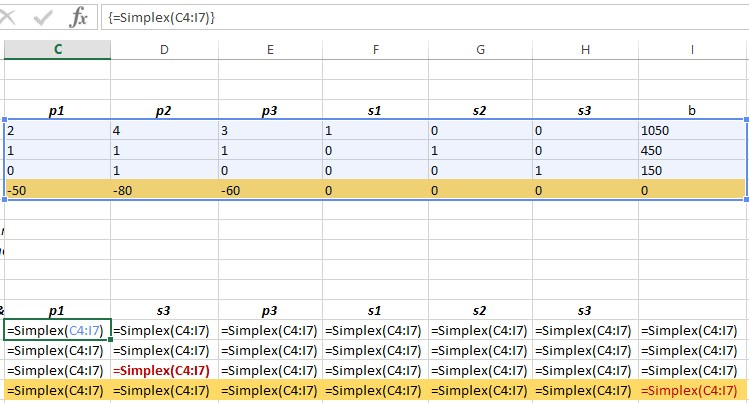
Array-Function-Macro

Tabellenkalkulation Simplex Code

Simplex Excel VBA Code[br]enter an arbitrary answer to see code

'# Copyright (C) 2018 H.W. Hofmann[br]'# This file is part of 'Simplex-Gauss-Algorithmus.xlsm'.[br]'#[br]'# Simplex-Gauss-Algorithmus.xlsm is free software: you can redistribute it and/or modify[br]'# it under the terms of the GNU General Public License as published by[br]'# the Free Software Foundation, either version 3 of the License, or[br]'# (at your option) any later version.[br]'#[br]'# VBA Simplex_LP Gauss LGS is distributed in the hope that it will be useful,[br]'# but WITHOUT ANY WARRANTY; without even the implied warranty of[br]'# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the[br]'# GNU General Public License for more details.[br]'#[br]'# Look at the GNU General Public License[br]'#Input as Array-Function > Start-Tableau =A1:L8[br]'#select input range A1:L8 > =Simplex(A1:L8) Strg+Alt+Enter[br]'#Result A1:L8={Simplex(A1:L8)}[br][br]Function Simplex(Tableau As Range)[br]Dim MM As Variant[br][br]'While negativ[br] MM = SimplexFindPivot(Tableau)[br] Simplex = SimplexBerechneTableau(Tableau, MM(1), MM(2))[br]'Wend[br][br]End Function[br][br][br]Function SimplexBerechneTableau(Tableau, ByVal pivotZeile As Integer, ByVal pivotSpalte As Integer)[br]Dim n%, m%, i%, j%, div As Double[br]Dim Tablo[br]n = Tableau.Rows.Count[br]m = Tableau.Columns.Count[br]ReDim Tablo(n, m)[br]Tablo = Tableau[br][br]div = Tablo(pivotZeile, pivotSpalte)[br][br]For j = 1 To m[br] Tablo(pivotZeile, j) = Tablo(pivotZeile, j) / div[br]Next[br]div = Tablo(pivotZeile, pivotSpalte)[br]For i = 1 To n[br] If i <> pivotZeile Then[br] div = Tablo(i, pivotSpalte)[br] For j = 1 To m[br] Tablo(i, j) = Tablo(i, j) - div * Tablo(pivotZeile, j)[br] Next[br] End If[br]Next[br][br]SimplexBerechneTableau = Tablo[br][br]End Function[br][br][br]Function SimplexFindPivot(Tablo)[br]Dim maxWert As Double, minWert As Double, div As Double[br]Dim n%, m%, i%, j%, pivotSpalte%, pivotZeile%[br]maxWert = 0[br]minWert = 10 ^ 15[br]n = Tablo.Rows.Count[br]m = Tablo.Columns.Count[br][br]For j = 1 To m - 1[br] If Tablo(n, j) < maxWert Then[br] maxWert = Tablo(n, j)[br] pivotSpalte = j[br] End If[br]Next[br][br]For i = 1 To n - 1[br] If Tablo(i, pivotSpalte) <> 0 Then[br] div = Tablo(i, m) / Tablo(i, pivotSpalte)[br] If (Tablo(i, pivotSpalte) > 0 And div < minWert) Or minWert = 0 Then[br] minWert = div[br] pivotZeile = i[br] End If[br] End If[br]Next[br][br]SimplexFindPivot = Array(pivotZeile, pivotSpalte)[br][br]End Function[br][br]

Tabellenkalkulation Simplex Code

Simplex Javascript 4 Google Sheet[br]enter an arbitrary answer to see code

/**[br]Simplex-Algorithmus Single Step für Google Sheets[br]@CustomFunction[br]=Simplex( Tableau )[br]Tableau Zellenbezug Anzahl Spalten>Zeilen[br]Tableau schrittweise bis zum Optimum Tableau[n-1][i]>0, iZeilen[br]Tableau mit pivotZeile pivotSpalte berechnen[br](C)2018 hawe[br]Version zu "Grundlagen Simplex Algorithmus" [br]+Zeilen/Spalten Index von 'SimplexFindPivot()' kompatibel zu Excel [br] Zeilen/Spalten Nummerierung beginnend mit 1[br]Array Function 4 Simplex [br]=ArrayFormula(SimplexBerechneTableau(D4:I7;3;1))[br]=ArrayFormula(Simplex(D4:I7))[br]*/[br]function SimplexBerechneTableau (tablo, pivotZeile, pivotSpalte){[br]var m = tablo[0].length; // Spalten[br]var n = tablo.length; // Zeilen[br]pivotZeile--;[br]pivotSpalte--; [br]var div = tablo[pivotZeile][pivotSpalte];[br][br]for(var j = 0; j < m; j++){[br] tablo[pivotZeile][j] = tablo[pivotZeile][j] / div;[br]};[br][br]div = tablo[pivotZeile][pivotSpalte];[br]for(var i = 0; i < n; i++){[br] if(i != pivotZeile ){[br] div = tablo[i][pivotSpalte];[br] for(j = 0; j < m; j++){[br] tablo[i][j] = tablo[i][j] - div * tablo[pivotZeile][j];[br] }[br] }[br]}[br]return tablo;[br]};[br][br] [br]/**[br]Finde Pivotzeile,Pivotspalte im Simplex-Tableau[br]@CustomFunction[br]=SimplexFindPivot( Tableau )[br]Tablo Zellenbezug Anzahl Spalten>Zeilen[br]liefert Zeilen-Array [0][Zeilenindex][Spaltenindex][br]für mit 1 beginnende Zeilen/Spalten-Nummerierung (kompatibel zu Excel)[br]*/ [br]function SimplexFindPivot( tablo ){[br]const Zeile = 0;[br]const Spalte = 1;[br]var maxWert = 0;[br]var minWert = 10000000000000;[br]var div = 0;[br]var pivot = new Array(1);[br] pivot[0] = new Array(2);[br]var m = tablo[0].length; // Spalten[br]var n = tablo.length; // Zeilen [br]pivot[0][Zeile] = 0;[br]pivot[0][Spalte] = 0;[br] [br]for(var j = 0; j < m-1; j++){[br] if(tablo[n-1][j] < maxWert){ // || nextPivot * (tablo[n-1][j] == maxWert) ){[br] maxWert = tablo[n-1][j];[br] pivot[0][Spalte] = j;[br] }[br]};[br]for(var i = 0; i < n-1; i++){[br] if( tablo[i][pivot[0][Spalte]] != 0 ){[br] div = tablo[i][m-1] / tablo[i][pivot[0][Spalte]];[br] if((tablo[i][pivot[0][Spalte]] > 0 && div < minWert) || minWert == 0 ){[br] minWert = div;[br] pivot[0][Zeile] = i;[br] }[br] }[br]};[br]// Kompatibel zu XL liefere Spalten-/Zeilen-Nummer zum Startindex 1[br]pivot[0][Zeile]++;[br]pivot[0][Spalte]++;[br] [br]return pivot;[br]}[br][br][br]function testsimple(){[br] var n = 3;[br] var m = 4; [br] [br] var tablo = new Array();[br] tablo[0]=[1,1,1,1,0,0,400];[br] tablo[1]=[3,2,2,0,2,0,800];[br] tablo[2]=[1,1,0,0,0,2,260];[br] tablo[3]=[-2,-2,-1,0,0,0,0];[br] [br] tablo = Simplex( tablo );[br] tablo = Simplex( tablo );[br] tablo = Simplex( tablo );[br] [br] tablo[3]=[-2,-2,-1,0,0,0,0];[br] [br]// for (var i = 0; i < n; i++) {[br]// tablo[i] = new Array(m);[br]// };[br] [br]// for (var i=0; i < n; i++){[br]// for (var j = 0; j < m; j++){[br]// tablo[i][j] = tablo[i][j];[br]// };[br]// };[br] [br][br]}[br][br][br]/** Copyright (C) 2018 H.W. Hofmann;[br]This file is part of 'Simplex-Gauss-Algorithmus.xlsm'.;[br]Simplex-Gauss-Algorithmus.xlsm is free software you can redistribute it and/or modify;[br]it under the terms of the GNU General Public License as published by;[br]the Free Software Foundation, either version 3 of the License, or;[br](at your option) any later version.;[br]VBA Simplex_LP Gauss LGS is distributed in the hope that it will be useful,;[br] but WITHOUT ANY WARRANTY; without even the implied warranty of;[br]MERCHANTABILITY || FITNESS FOR A PARTICULAR PURPOSE. See the;[br]GNU General Public License for more details.;[br]Look at the GNU General Public License;[br]*/

Simplex Algorithmus MAX Programm

SimplexAlgorithmusIntegerMAX

Beispiele

Lösungsraum mit den Ergebnissen der Simplex Tableaus

Beispiel mit TabCalc (MS Excel/Google Sheet

Tabellenkalkulation Simplex Code

Tabellenkalkulation Simplex Code

Information: Simplex Algorithmus MAX Programm