Discovery Lessons (Interactive)

Tim Brzezinski, Sep 29, 2016

[color=#1551b5]Contains a sampler of several Geometry lessons where students actively use GeoGebra to DISCOVER many theorems and other principles/concepts for themselves. Many of the worksheets in this book contain PDF copies of the discovery lessons I have used, much to students' success, within my classes. For an exhaustive resource containing over 400 worksheets mapped to one (or more) of the CCSS-High School: Geometry standards, go to [url]https://www.geogebra.org/m/yCs9zxry[/url][/color]

Table of Contents

  1. Introductory Discoveries
    1. Slope Illustrator
    2. Blueprint Equation of a Line (I)
  2. Quick Assessments of Introductory Discoveries
    1. Slope (Quiz) I
    2. Slope (Quiz) II
    3. Graphing Linear Equations: Question Generator (V2)
    4. Writing the Equation of a Line (I-VA)
  3. Discovery Learning Labs (Less Scaffolding)
    1. Isosceles Triangle Theorem: Discovery Lab
    2. Converse of IST: Template
    3. Parallelogram Construction Template & Discovery Lab
    4. Points of Concurrency: Investigation
    5. Parallel Lines Proportionality Theorem
    6. Square Template with Investigation Questions
    7. Tangents to Circles: Investigation
    8. Angle -Angle: Triangle Investigation
  4. Discovery Learning Labs (More Scaffolding)
    1. Vertical Angles Exploration (1)
    2. Vertical Angles Exploration (2)
    3. Triangle Medians: Quick Investigation
    4. Square Template (Scaffolded Investigation)
    5. Where to Sit? (I)
    6. Where to Sit (II)?
  5. Locus Tasks (Less Scaffolding)
    1. Interesting Coplanar Locations (1)
    2. Interesting Coplanar Locations (2)
    3. Locus Construction 1
    4. Locus Construction 2
    5. Locus Construction 3
  6. Locus Tasks (More Scaffolding)
    1. Locus Problem (1)
    2. Locus Problem (2)
    3. Locus Problem (3)

1.

Introductory Discoveries

  • 1. Slope Illustrator
  • 2. Blueprint Equation of a Line (I)

1.1.

Slope Illustrator

Move the two points around to change the slope of the line. Be sure to press the EXPLORE BUTTON when you see it appear. After doing so, move the new colored point (that will appear) around.
– Tim Brzezinski

1.2.

–

2.

Quick Assessments of Introductory Discoveries

  • 1. Slope (Quiz) I
  • 2. Slope (Quiz) II
  • 3. Graphing Linear Equations: Question Generator (V2)
  • 4. Writing the Equation of a Line (I-VA)

2.1.

Slope (Quiz) I

[b]Directions:[/b][br][br]1) In the applet below, [b]note the slope displayed.[/b][br]2) Drag one (or both) of the white points to move the line [b]so that this line has this slope.[br][/b][br]3) Click the [b]"Check Your Graph"[/b] checkbox to determine if you're correct. [br] If the slope of your line matches the slope displayed, you'll see a [color=#ff00ff][b][i]"CORRECT"[/i][/b][/color] sign appear. [br] If your line does not have the slope displayed, you'll see a [b]"Not Correct"[/b] sign appear. [br] If this happens, try again. If you need a refresher, [url=https://www.geogebra.org/m/Xutr9rPj]click here[/url]. [br]
– Tim Brzezinski

2.2.

–

2.3.

–

2.4.

–

3.

Discovery Learning Labs (Less Scaffolding)

  • 1. Isosceles Triangle Theorem: Discovery Lab
  • 2. Converse of IST: Template
  • 3. Parallelogram Construction Template & Discovery Lab
  • 4. Points of Concurrency: Investigation
  • 5. Parallel Lines Proportionality Theorem
  • 6. Square Template with Investigation Questions
  • 7. Tangents to Circles: Investigation
  • 8. Angle -Angle: Triangle Investigation

3.1.

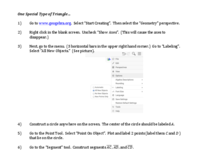
Isosceles Triangle Theorem: Discovery Lab

[color=#000000]Use the applet below to serve as the template for your [/color][color=#0000ff][b][i]One Special Type of Triangle [/i][/b][/color][color=#000000]Investigation. [br][/color][b][color=#cc0000]The PDF file of [/color][color=#0000ff]this investigation[/color][color=#cc0000] can be found BELOW THE APPLET.[/color][/b]
Isosceles Triangle Theorem & Theorems (GeoGebra)
– Tim Brzezinski

3.2.

–

3.3.

–

3.4.

–

3.5.

–

3.6.

–

3.7.

–

3.8.

–

4.

Discovery Learning Labs (More Scaffolding)

  • 1. Vertical Angles Exploration (1)
  • 2. Vertical Angles Exploration (2)
  • 3. Triangle Medians: Quick Investigation
  • 4. Square Template (Scaffolded Investigation)
  • 5. Where to Sit? (I)
  • 6. Where to Sit (II)?

4.1.

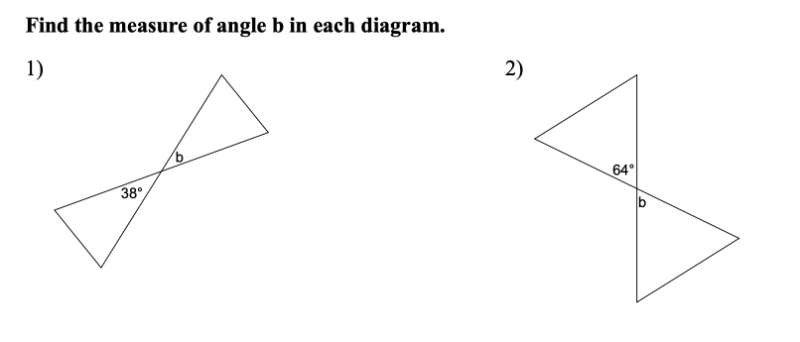
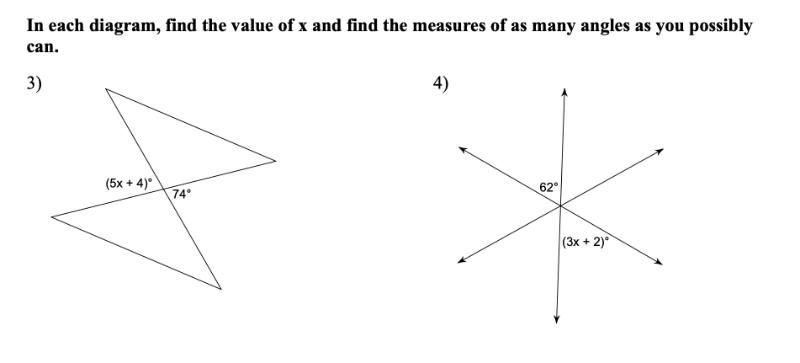
Vertical Angles Exploration (1)

Interact with this app for a few minutes. Be sure to drag the LARGE POINT around and be sure to move the 2 sliders you see.
Notice anything interesting? Describe as best as you can.
What happens if you make the size of the [b][color=#ff00ff]angle[/color][/b] BIGGER or smaller? [br][br][b][color=#ff00ff](You can change the size of the manila angle by using the manila-colored slider). [/color][/b]Does your response to the question above change? Why? Why not? Describe.
– Tim Brzezinski

4.2.

–

4.3.

–

4.4.

–

4.5.

–

4.6.

–

5.

Locus Tasks (Less Scaffolding)

  • 1. Interesting Coplanar Locations (1)
  • 2. Interesting Coplanar Locations (2)
  • 3. Locus Construction 1
  • 4. Locus Construction 2
  • 5. Locus Construction 3

5.1.

Interesting Coplanar Locations (1)

Interesting Coplanar Locations
– Tim Brzezinski

5.2.

–

5.3.

–

5.4.

–

5.5.

–

6.

Locus Tasks (More Scaffolding)

  • 1. Locus Problem (1)
  • 2. Locus Problem (2)
  • 3. Locus Problem (3)

6.1.

Locus Problem (1)

In the applet below, [br][br][i][color=#1e84cc][b]F[/b][/color][/i][color=#1e84cc][b] is a point[/b] [/color]that is not on line [i]d[/i]. [br][b]Point [i]D[/i] is a point that lies ON [color=#666666]the line that passes through [i]A [/i]and [i]B[/i][/color]. [br][/b]The [color=#ff00ff][b]pink line[/b][/color] is the [color=#ff00ff][b]perpendicular bisector[/b][/color] of the segment with endpoints [i][color=#1e84cc][b]F[/b][/color][/i] and [i][b]D[/b][/i]. [br][br]Drag [b]point [i]D[/i][/b] along the line. What do you see? Describe in detail! [br] [br]Feel free to alter the locations of [color=#666666][i][b]A,[/b][/i][/color] [i][color=#666666][b]B[/b][/color], [/i]and/or [i][color=#1e84cc][b]F[/b][/color][/i][color=#666666]. [br][/color]Then [color=#38761d][b]clear the trace[/b][/color] and drag [b]point [i]D[/i][/b] along [color=#666666][b]the line[/b][/color] again. [br][br]Why does this occur?
Please go to the [url=https://www.geogebra.org/m/sduBXC6P]Locus Construction 1 Task[/url] and begin!
– Tim Brzezinski

6.2.

–

6.3.

–

Information