Einführung GeoGebra

Georg Wengler, Jul 22, 2015

Eine Einführung in die Komponenten von GeoGebra.

Table of Contents

  1. Geometrie
    1. Die Werkzeugleiste
    2. Rechteck
    3. Dreieck mit Umkreis
    4. Merkwürdige Punkte im Dreieck
    5. Pointieren
    6. Dynamisieren
    7. Kommentieren
    8. Beweis ohne Worte
    9. Aufgabe 01
    10. Aufgabe 02
    11. Aufgabe 03
    12. Aufgabe 04
    13. Aufgabe 05
    14. Aufgabe 06
    15. Aufgabe 07
    16. Aufgabe 08
    17. Aufgabe 09
    18. Aufgabe 10
  2. Algebra
    1. Mathematische Funktionen
    2. GGB-Befehle
    3. Liste von Objekten
    4. Folge-Befehl
    5. Skalieren
    6. Uhr beschriften
  3. Tabelle
    1. Wertetabelle
  4. 3D
    1. Würfelnetz dynamisch
  5. CAS
    1. Gleichung lösen
  6. Skripting
    1. Animationsknopf
    2. Spur, Ortslinie und analytische Kurve
    3. Animation und Spur

1.

Geometrie

Aufbau der Werkzeugleiste für Elementargeometrie

  • 1. Die Werkzeugleiste
  • 2. Rechteck
  • 3. Dreieck mit Umkreis
  • 4. Merkwürdige Punkte im Dreieck
  • 5. Pointieren
  • 6. Dynamisieren
  • 7. Kommentieren
  • 8. Beweis ohne Worte
  • 9. Aufgabe 01
  • 10. Aufgabe 02
  • 11. Aufgabe 03
  • 12. Aufgabe 04
  • 13. Aufgabe 05
  • 14. Aufgabe 06
  • 15. Aufgabe 07
  • 16. Aufgabe 08
  • 17. Aufgabe 09
  • 18. Aufgabe 10

1.1.

Die Werkzeugleiste

Komponenten der Werkzeugleiste
[icon]/images/ggb/toolbar/mode_point.png[/icon]Punkt: markieren, bewegen, formatieren - Mittelpunkt[br][icon]/images/ggb/toolbar/mode_join.png[/icon]Gerade: lineare Gebilde[br][icon]/images/ggb/toolbar/mode_orthogonal.png[/icon]Konstruktionen: Senkrechte, Parallele, Streckensymmetrale, Winkelsymmetrale[br][icon]/images/ggb/toolbar/mode_polygon.png[/icon]Vielecke[br][icon]/images/ggb/toolbar/mode_circle2.png[/icon]Kreis: Der Kreis und seine Teile[br][icon]/images/ggb/toolbar/mode_ellipse3.png[/icon]Kegelschnitte[br][icon]/images/ggb/toolbar/mode_angle.png[/icon]Bemaßung: Winkel, Länge, Flächeninhalt[br][icon]/images/ggb/toolbar/mode_mirroratline.png[/icon]Abbildungen: Spiegeln, Drehen, Verschieben, zentrisch Strecken[br][icon]/images/ggb/toolbar/mode_text.png[/icon]Text und Bild [icon]/images/ggb/toolbar/mode_image.png[/icon][br][icon]/images/ggb/toolbar/mode_slider.png[/icon]Steuerelemente: Schieberegler, Kontrollkästchen, Schaltknopf, Eingabefeld[br][icon]/images/ggb/toolbar/mode_translateview.png[/icon]Sonstiges: Bewegen, Zoomen, Anzeigen, Format übertragen, Löschen
Erste Schritte mit GeoGebra
Aufgabe: [br][list=1][*]Zeichne einen Punkt P [/*][*]Zeichne eine Gerade g, die nicht durch P geht.[/*][*]Errichte die Normale n von P auf g.[/*][*]Markiere den Schnittpunkt S von n mit g.[/*][*]Zeichne den Kreis k mit Mittelpunkt P durch den Punkt S.[/*][*]Schraffiere die Kreisfläche.[/*][*]Wähle einen Punkt K auf dem Kreis.[/*][*]Zeichne die Strecke s = PK und schalte die Spur ein.[/*][*]Animiere den Punkt K.[/*][*]Schalte die Spur und die Animation wieder aus.[/*][/list]
– Georg Wengler

1.2.

–

1.3.

–

1.4.

–

1.5.

–

1.6.

–

1.7.

–

1.8.

–

1.9.

–

1.10.

–

1.11.

–

1.12.

–

1.13.

–

1.14.

–

1.15.

–

1.16.

–

1.17.

–

1.18.

–

2.

Algebra

GeoGebra-Befehle in der Eingabezeile editieren.

  • 1. Mathematische Funktionen
  • 2. GGB-Befehle
  • 3. Liste von Objekten
  • 4. Folge-Befehl
  • 5. Skalieren
  • 6. Uhr beschriften

2.1.

Mathematische Funktionen

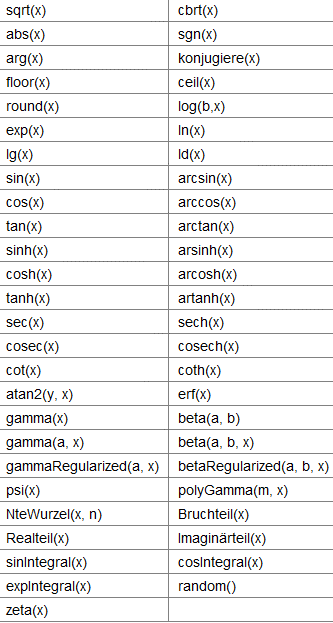
Funktionseingabe
Probieren Sie die mathematischen Funktionen aus, indem Sie sie im Eingabefeld eintragen[br]und diskutieren Sie den Verlauf des Graphen.
– Georg Wengler

2.2.

–

2.3.

–

2.4.

–

2.5.

–

2.6.

–

3.

Tabelle

Die Funktionen der Tabelle kennenlernen.

  • 1. Wertetabelle

3.1.

Wertetabelle

Die Tabelle funktioniert im Prinzip wie eine Tabellenkalkulation.[br]Allerdings gelten auch noch alle GGB-Befehle.[br][br]Beispiel:[br]Die Funktion y = kx +d soll tabelliert werden.[br][list=1][*]k,d als Schieberegler anlegen.[/*][*]Zellen in der Tabelle wie folgt belegen:[br]A1 ="x"[br]B1 ="y"[br]A2 =0[br]A3 = A2+1   Kopieren bis Zelle A12[br]B2 =k*A2+d Kopieren bis Zelle B12[/*][*]Zellbereich A1..B12 markieren und als Tabelle erzeugen[/*][*]Zellbereich A2..B12 markieren und als Liste von Punkten erzeugen[/*][/list][br]Im Grafikfenster sind eine Wertetabelle und die Punkte sichtbar.
Versuch es selber ...
– Georg Wengler

4.

3D

Darstellung von Körpern in 3d-Ansicht.

  • 1. Würfelnetz dynamisch

4.1.

Würfelnetz dynamisch

Im 3d-Grafikfenster soll ein Würfel mit Netz gezeichnet werden:[br][list=1][*]A=(0,0,0) und B=(1,0,0) zeichnen[/*][*]Würfel auswählen und über AB zeichnen[/*][*]Netz auswählen (Schieberegler wird automatisch angelegt)[/*][/list]
Versuche es selber ...
– Georg Wengler

5.

CAS

Einführung in das Algebrasystem von GeoGebra.

  • 1. Gleichung lösen

5.1.

Gleichung lösen

Eine Gleichung mit Hilfe von CAS lösen:[br][list=1][*]Löse[<Gleichung>,<Variable>] liefert explizite Lösung(en).[/*][*]Lösungen[<Gleichung>,<Variable>] liefert eine Liste der Lösung(en)[/*][*]KLöse[] bzw. KLösungen[] liefern komplexe Lösungen[/*][*]Löse[{<gl1>,<gl2>},{<var1>,<ver2>}] löst ein Gleichungssystem[/*][*]Lösungen[{<gl1>,<gl2>},{<var1>,<ver2>}] liefert eine Matrix[br][/*][/list]
Versuche es selber ...
– Georg Wengler

6.

Skripting

  • 1. Animationsknopf
  • 2. Spur, Ortslinie und analytische Kurve
  • 3. Animation und Spur

6.1.

Animationsknopf

Eine Animation (Punkt auf Kreis) soll per Schaltknopf gestartet bzw. angehalten werden können.[br][br]Beispiel: P wandert auf Kreis k.[br][list=1][*]k:=Kreis[(0,0),5] zeichnen[/*][*]P:=Punkt[k] auf Kreis legen.[/*][*]anim:=false[/*][*]Schaltfläche1 anlegen mit der Aufschrift "Start"[/*][*]Gehe über Eigenschaften von der Schaltfläche1 zu Skripting[/*][*]Trage folgenden Script bei Mausklick ein.[br]anim=!anim[br]StartAnimation[P,anim][br]SetzeBeschriftung[Schaltfläche1,Wenn[anim,"Stop","Start"]][/*][/list]
Versuche es selber ...
– Georg Wengler

6.2.

–

6.3.

–

Information