transformaties
Table of Contents
- Transformaties
- Transformatie herkennen
- Spiegeling
- Wat is een spiegeling?
- Een spiegeling tekenen
- Een spiegeling tekenen met geodriehoek
- Verschuiving
- Wat is een verschuiving?
- Een verschuiving tekenen
- Een verschuiving tekenen met geodriehoek
- Draaiing
- Draaiing reuzenrad
- Een draaiing tekenen
- Een draaiing tekenen met geodriehoek
- Eigendraaiing
- Samenvatting
- Samenvatting spiegeling, verschuiving, draaiing tekenen.
Transformatie herkennen
Wat is een spiegeling?
Spiegels en spiegelbeelden ken je uit het dagelijks leven. Hier leer je wat een spiegeling in de wiskunde betekent. [br][br]
Teken een punt A. [br][br][icon]/images/ggb/toolbar/mode_point.png[/icon] en klik op het scherm waar je het punt wil. Rechterklik op het punt en klik 'Toon label' aan om de naam van het punt te zien. [br][br]Teken een rechte (spiegelas) waarrond je punt A zal spiegelen. [br][br][icon]/images/ggb/toolbar/mode_join.png[/icon] en klik 2x op het scherm om een rechte te tekenen (een rechte wordt bepaald door 2 punten). [br][br]Het programma kan spiegelbeelden tekenen ten opzichte van een gegeven rechte. Dit doe je zo:[br][br][icon]/images/ggb/toolbar/mode_mirroratline.png[/icon] Klik eerst op het punt (of object) dat je wil spiegelen. Klik daarna op de rechte waarrond je wil spiegelen (de spiegelas). Het spiegelbeeld van A (A') verschijnt nu. [br][br]Versleep het punt A en kijk wat er gebeurt. [br][icon]/images/ggb/toolbar/mode_move.png[/icon] Klik op het punt, blijf vasthouden en beweeg je muis. [br][br]Verbind de punten A en A'. [br][icon]/images/ggb/toolbar/mode_join.png[/icon] en [icon]/images/ggb/toolbar/mode_segment.png[/icon] en klik op de 2 punten. Beweeg punt A nogmaals. [br][br]Welke merkwaardige lijn is de spiegelas ten opzichte van A en A'? [br][br]
Wat is een verschuiving?
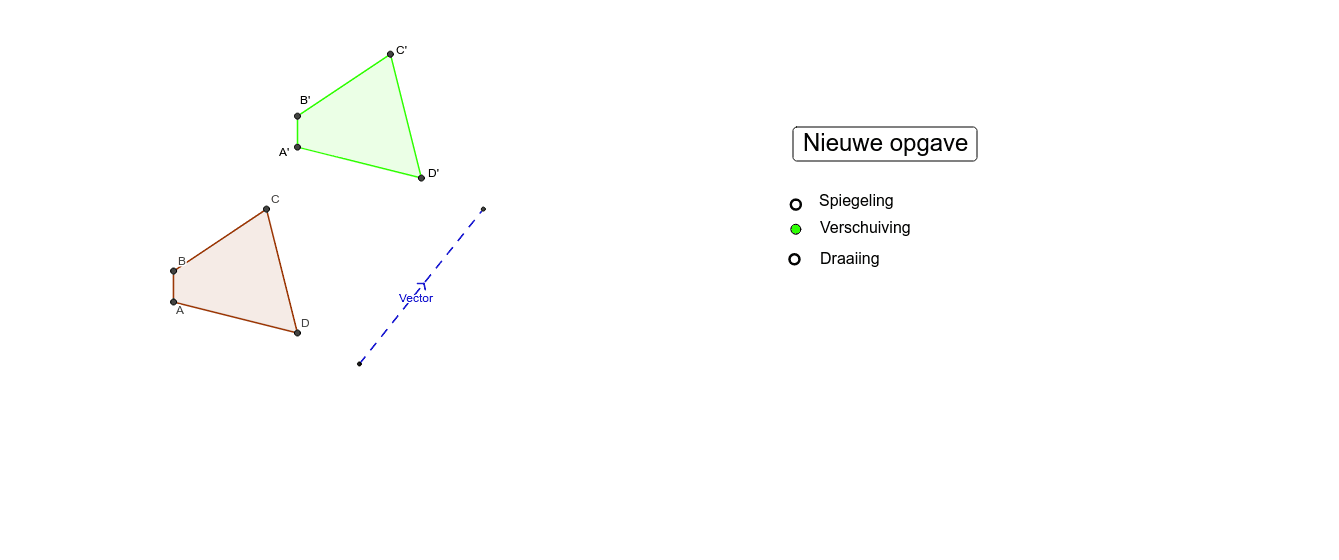
Teken een punt A. [br][br][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon] en klik op het scherm waar je het punt wil. Rechterklik op het punt en klik op 'Toon label' om de naam van het punt te zien. [br][br]Het programma kan punten, lijnstukken, figuren, enz. verschuiven ten opzichte van een vector. [br]Dit doe je zo:[br][br][icon]/images/ggb/toolbar/mode_mirroratline.png[/icon] en [icon]/images/ggb/toolbar/mode_vectorfrompoint.png[/icon]. Klik eerst op het punt (of object) dat je wil verschuiven. Klik daarna op de vector die de lengte, richting en zin van de verschuiving aangeeft (deze termen bekijken we nog).[br][br]Versleep het punt Y van de vector en kijk wat er gebeurt. [br][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon] Klik op het punt, blijf vasthouden en beweeg je muis. [br][br]Verbind de punten A en A'. [br][icon]https://www.geogebra.org/images/ggb/toolbar/mode_join.png[/icon] en [icon]https://www.geogebra.org/images/ggb/toolbar/mode_segment.png[/icon] en klik op de 2 punten. Maak er een stippellijn van:[br][br]Rechterklik op het lijnstuk --> eigenschappen --> stijl --> lijnsoort --> kies een stippellijn. [br][br]Versleep Y nog eens. Wat kan je zeggen over de lengte en de onderlinge ligging van [XY] en [AA']?[br]