Ecritures fractionnaires
Table of Contents
- Ecritures fractionnaires d’un quotient (Révision de 6e)
- 1) Définitions:
- 2) Tableau récapitulatif :
- Divisibilité ( révision de 6e):
- 1) Définitions
- 2) Critères de divisibilité par 2 ; 5 ; 4 ; 3 et 9
- Proportion
- Définition :
- Quotient égaux
- 1°) Propriété
- 2°) Simplifier une fraction
- Comparaison de deux nombres en écriture fractionnaire
- 1°) Les écritures fractionnaires ont le même dénominateur
- 2°) Les écritures fractionnaires ont le même numérateur
- 3°) Cas général
1) Définitions:
La notation [math]\frac{\red{a}}{\red{b}}[/math][color=#ff0000] (b≠0)[/color] est une écriture fractionnaire.[br]Le nombre [color=#ff0000]a[/color] est le [color=#ff0000]numérateur[/color].[br]Le nombre [color=#ff0000]b[/color] est le [color=#ff0000]dénominateur[/color].
Lorsque a et b (b [color=#ff0000]≠[/color] 0) sont des nombres entiers, l’écriture fractionnaire [math]\frac{\red{a}}{\red{b}}[/math]est appelée [color=#ff0000]fraction[/color] .
Exemples :
[math]\frac{3}{4}[/math]est une fraction : [b]3[/b] est son [b]numérateur[/b] et [b]4[/b] est son [b]dénominateur[/b][br][math]\frac{3,2}{7,8}[/math]est une écriture fractionnaire : 3,2 est son numérateur 7,8 est son dénominateur.
1) Définitions
Un nombre [color=#ff0000]a[/color] est un [color=#ff0000]multiple[/color] d’un nombre b ( b ≠ 0) lorsque le [color=#ff0000]reste[/color] de la [color=#ff0000]division euclidienne[/color] de [color=#ff0000]a[/color] par [color=#ff0000]b[/color] est égale à [color=#ff0000]0[/color].
Exemples
Remarque :
[b]On dit aussi que :[/b][br]4 est un [color=#ff0000]diviseur de[/color] 8 7 est un [color=#ff0000]diviseur de[/color] 217[br]8 est [color=#ff0000]divisible par[/color] 4 217 [color=#ff0000]est divisible par[/color] 7
Définition :
Pour [color=#ff0000](b≠0)[/color],[math]\frac{\textcolor{red}{a}}{\textcolor{red}{b}} [/math] désigne une proportion.
Exemple :
Parmi les 24 élèves de la classe de 5ème 8, 17 élèves sont demi-pensionnaires.[br][math]\frac{17}{24}[/math]est la proportion d’élèves demi-pensionnaires dans la classe
1°) Propriété
1°) Propriété
[code][/code][code][/code]Si on multiplie ou divise le numérateur et le dénominateur d’une écriture[br]fractionnaire par un même nombre (non nul) on obtient une écriture[br]fractionnaire égale [br][center][math]\frac{a}{b}=[/math]=[math]\frac{a\textcolor{red}{\times k}}{b\textcolor{red}{\times k}}[/math]ou[math]\frac{a}{b}=[/math]=[math]\frac{a\textcolor{red}{\div k}}{b\textcolor{red}{\div k}}[/math] avec [br][math]\textcolor{red}{b\ne0}[/math] [color=#ff0000]et[/color][math]\textcolor{red}{k\ne0}[/math][/center]
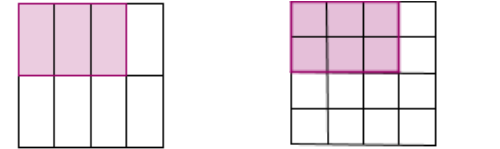
Exemples graphiques
[br][table][tr][td]On a colorié les [color=#1551b5][math]\textcolor{red}{\frac{3}{8}}[/math][/color] du carré[/td][td] On a colorié les [color=#1551b5][math]\textcolor{red}{\frac{6}{16}}[/math][/color] du carré[/td][/tr][tr][td]On a colorié la même quantité[br][/td][td]et[math]\frac{3}{8}=\frac{3\textcolor{red}{\times2}}{8\textcolor{red}{\times2}}=\frac{6}{16}[/math][/td][/tr][/table][br]Exemples numériques :[br][br][math]\frac{8}{5}=\frac{8\textcolor{red}{\times7}}{5\textcolor{red}{\times7}}=\frac{56}{35}[/math] [math]\frac{7,95}{8,1}=\frac{7,95\textcolor{red}{\times100}}{8,1\textcolor{red}{\times100}}=\frac{795}{800}[/math] [math]\frac{21}{56}=\frac{21\textcolor{red}{\div7}}{56\textcolor{red}{\div7}}=\frac{3}{8}[/math][br][br]
1°) Les écritures fractionnaires ont le même dénominateur
Propriété :
Si deux nombres en écriture fractionnaire ont le [color=#ff0000]même dénominateur[/color] alors [color=#ff0000]le plus petit[/color] est celui qui a [color=#ff0000]le plus petit numérateur[/color] :[br][br]Si a < b alors[math]\frac{a}{\textcolor{red}{c}}[/math]<[math]\frac{b}{\textcolor{red}{c}}[/math] avec (c ≠ 0)[br][br]Exemples:[br][br][math]\frac{7}{8}[/math]<[math]\frac{13}{8}[/math] car 7 < 13 et [math]\frac{11}{20}[/math]>[math]\frac{3}{20}[/math] car 11 > 3