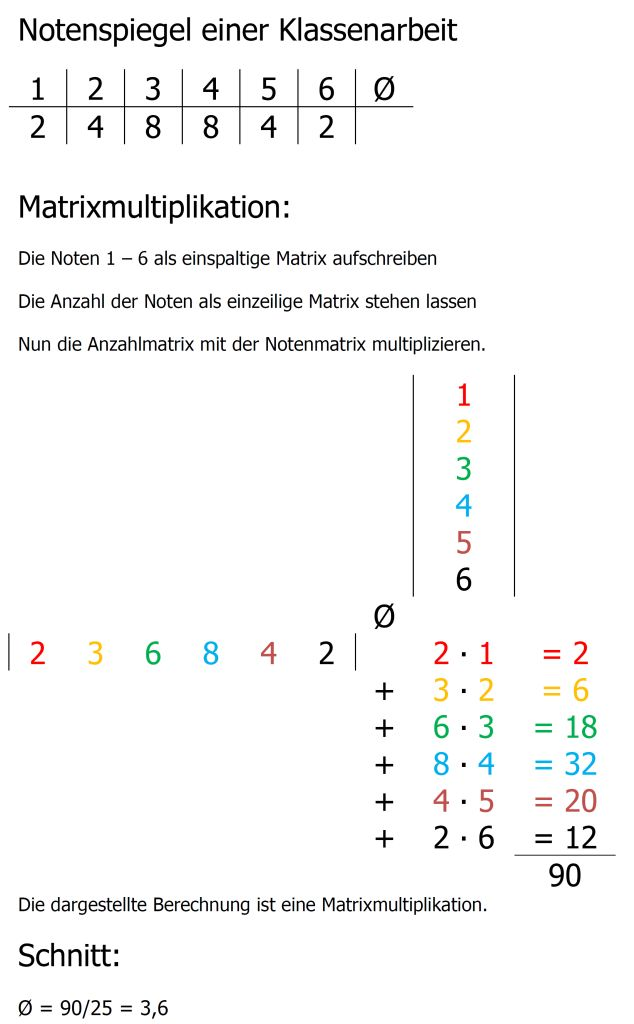
Damit zwei Matrizen [math]A[/math] und [math]B[/math] miteinander multipliziert werden können, muss die Matrix [math]A[/math] so viele Spalten haben, wie die Matrix [math]B[/math] Zeilen hat.[br]Es muss [math]n_A=m_B[/math] erfüllt sein, sonst können die Matrizen nicht miteinander multipliziert werden.[br][br]Zu beachten ist, dass die Matrixmultiplikation nicht kommutativ ist![br]In der Regel gilt: [math]A\cdot B\ne B\cdot A[/math][br][br]Die Ergebnismatrix der Multiplikation hat immer so viele Zeilen, wie die erste Matrix und so viele Spalten wie die zweite Matrix.[br][br]Die einzelnen Elemente der Ergebnismatrix werden berechnet, indem die jeweiligen Elemente der Ausgangsmatrizen multipliziert und die Teilprodukte addiert werden.[br]Das klingt sehr kryptisch, ist aber nicht schwer.[br]In der Beispielaufgabe wurde bereits eine Matrixmultiplikation durchgeführt und nachgeschlagen werden.[br][br]Veranschaulichen lässt sich die Berechnung der einzelnen Matrixelemente mit der Berechnung des Notenschnitts einer Klassenarbeit. Um den Notenschnitt zu Berechnen, wird eine Matrixmultiplikation durchgeführt.[br](Um den Schnitt zu erhalten muss das Matrixprodukt noch durch die Anzahl der Schüler und Schülerinnen dividiert werden.)