
Die Hypotenuse berechnen
[u][b][color=#1e84cc]1. Aufgabe[/color][/b][/u][br][br]Wie kommt man nun von Satz des Pythagoras [b]c² = a² + b² [/b]auf die Länge der Hypotenuse? Forme den Satz des Pythagoras um und trage deine Antwort ein und überprüfe sie![br][br]Solltest du auf eine andere Formel gekommen sein, schreibe dir die richtige Formel auf![br][br][u]Hinweis:[/u] Überlege dir, wie du die Gleichung umformen muss um nur [b]c [/b]auf der linken Seite stehen zu haben.
[b][u][color=#1e84cc]2. Aufgabe[/color][/u][/b] [br][br]Gegeben ist ein rechtwinkliges Dreieck mit den Katheten a = 4 cm und b = 5 cm. Berechne die Hypotenuse und trage dein Ergebnis auf 1 Dezimalstelle gerundet ein!
[b][u][color=#1e84cc]3. Aufgabe [/color][/u][/b][br][br]Berechne die fehlende Seite des Dreiecks aus der Skizze!

[u][b][color=#1e84cc]4. Aufgabe[br][br][/color][/b][/u][color=#1e84cc][b]a) [/b][/color]Gegeben ist ein Quadrat mit der Seitenlänge a = 3,5 cm. Berechne die Länge der Diagonale d, überleg dir davor, wo du rechtwinklige Dreiecke findest. (Runde auf 2 Dezimalstellen genau!)
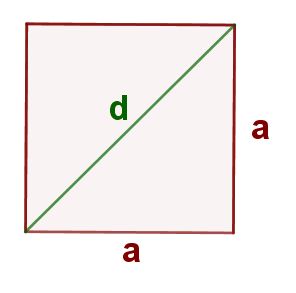
[color=#1e84cc][b]b)[/b][/color] Wie lässt sich die Form für die Diagonale vom Quadrat verallgemeinern? Schreibe deine Formel auf und trage sie als Antwort ein.