Deterministic model
We have already worked our way through the
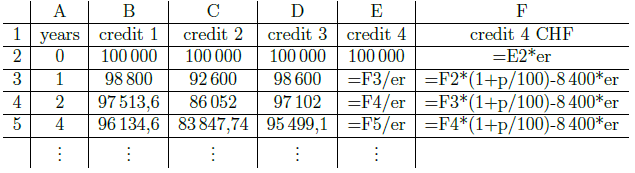
first two steps, so it remains to implement[br]the GeoGebra applet. In this model we quickly create two sliders in GeoGebra, one for[br]the key interest rate p and the other for the exchange rate er. In the spreadsheet-view[br]one calculates the yearly debt level for the four credits by using the recurrence relation[br](1). For Example in cell B1 one
nds the formula "=B2*(1+p/100)-8 400", analogous[br]calculations for credit 2 (pay attention to the
rst two periods!) and credit 3 (use if-[br]statements!). The calculations of credit 4, see table 1, lead to the same yearly debt levels[br]as for credit 1.
Table 1

We follow the idea of Heugl and create a list of points for every credit (see [3], p. 76).[br]The result is a nice visualization of the yearly debt levels of each credit. Different point[br]styles enable easy distinguishing between the four credits.
Figure 2.1
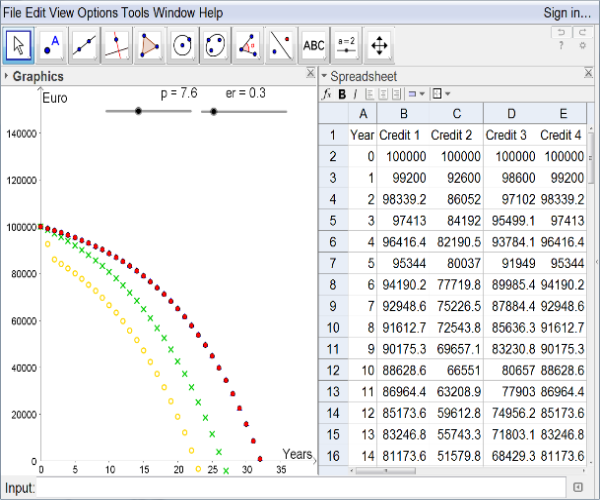
Figure 2.2
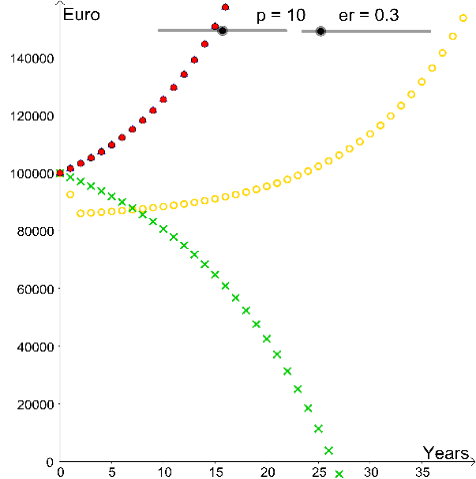
In school a stage of experiments might be of advantage, like manipulating slider bars[br]and observing its outcomes. In case of less experienced pupils the teacher should prepare[br]guiding questions, e.g. "What will happen, if the value of the key interest rate in-[br]creases/decreases?" or "At which values is credit 1 better than credit 2?" These heuristic[br]observations can be collected and shared in class.[br]Afterwards there is an opportunity to justify some of these
findings by using mathe-[br]matical argumentations. In this deterministic model one gets for every value of the key[br]interest rate p one best credit or for some values p two best credits, see below.
One gets such values by pairwise comparing the credits. For example one obtains 1.477[br]by using the equation (2) of credit 1 and 2 (slightly modified) and set S[sub]n[/sub] = 0. We express[br]the number of years n explicitly. In case of credit 1 we get per CAS (for convenience we[br]set q := 1 + p/100 ):
[math]n=\frac{ln\left(\frac{8400}{8400-\left(q-1\right)\cdot100000}\right)}{ln\left(q\right)}[/math]
[math]n=\frac{ln\left(\frac{q^2\cdot8400}{\left(1.02\cdot\left(q-1\right)+q\right)\cdot8400-1.01\cdot1.02\cdot\left(q-1\right)\cdot100000}\right)}{ln\left(q\right)}[/math]
We equal the two terms of the equations (3) and (4) and solve the resulting equation for[br]the variable q. Finally, we obtain q = 1.01477 and therefore p = 1.477.[br]In a validation of this model one will recognize some of its wrong results. It is impossible[br]that the yearly debt level of the foreign currency loan equals the yearly debt level of[br]credit 1. Empirical investigations like reading newspaper reveal this mistake in the model[br]above. Foreign currency loans have a bad press, actually in Austria they are forbidden[br]for hypothecary credits.