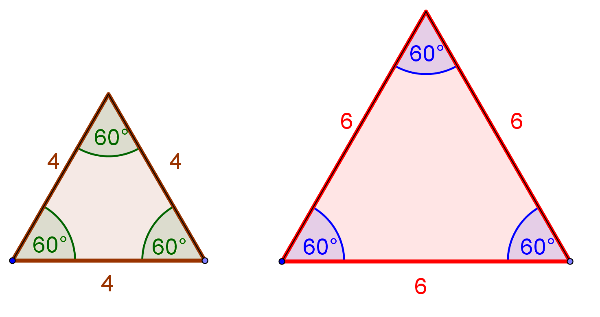
Look at the illustration below:

The AAA combination will show that the triangles are the same SHAPE (similar), but will [b]NOT[/b] show that the triangles are the same size. [i][br][br]Example: [/i]Consider the two equilateral triangles above that satisfy the AAA combination. They are the same shape, but are not the same size. Thus, they are not congruent. (They are similar.)[br][br]Yes,it is possible that the sides "could" be the same length and the[br]triangles would be congruent, but this would be the exception, not the rule.[br][br][b][color=#ff0000]If we prove AAA we are proving similarity and not necessary congruency.[/color][/b][br][br][b]Click here:[color=#0000ff] [/color][/b][url=http://www.sparknotes.com/math/geometry2/congruence/section5.rhtml][color=#0000ff][b]Read more about proving triangles to be similar.[/b][/color][/url]