De methode met vergelijkingen die Ian Gambini beschrijft is wel de manier waarop 15 jaar na Moróns bijna-vierkant een student het probleem kraakte.

William Tutte was een Brits wiskundige die reeds als student aan het probleem werkte en er in 1940 over publiceerde. Het zal geen toeval zijn dat hij tijdens de Tweede Wereldoorlog belangrijk werk leverde als ontcijferaar van geheime militaire codes.[br]Hij pakte het vierkantprobleem aan door een niet-schaalgetrouwe schets te maken en te starten vanuit twee vierkanten met als zijden x en y. Het laatste, sluitende vierkant moet een vergelijking opleveren in x en y waaruit we een oplossing kunnen afleiden.

We kunnen het laatste vierkant oplossen door horizontaal en verticaal het saldo te maken.[br][u]horizontaal[/u]:[br][list][*]Onderaan is het saldo 6x + 9y.[/*][*]Bovenaan hebben we al 11y.[/*][*]Het saldo klopt als we als afmeting voor het rode vierkant [b]6x - 2y[/b] nemen.[/*][/list][u]verticaal[/u]:[br][list][*]Links is het saldo 2x + 16y.[/*][*]Rechts hebben we al 5x + 2y.[/*][*]Het saldo klopt als we als afmeting voor het rode vierkant [b]-3x + 14y[/b] nemen.[/*][/list]We krijgen dus als vergelijking:[br]6x - 2y = -3x + 14 [br]9x = 16 [br]De meest eenvoudige oplossing hiervan is [b]x = 16 en y = 9[/b]

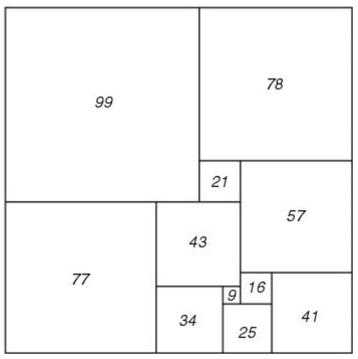
In de ontwerpschets vervangen we nu x en y door de gevonden waarden, zodat we het perfecte vierkant in zijn juiste verhoudingen kunnen tekenen: