[justify]Nesse etapa será apresentado o Software GeoGebra de forma geral e generalizada. será feito uma breve abordagem de seu desenvolvimento, apresentamos sua interface, algumas funcionalidades e os passos necessários para construção de alguns objetos. [/justify]
[justify]O software GeoGebra possui propósitos didáticos para ser empregado em situações de ensino e aprendizagem de matemática, e outras disciplinas. A partir de seus recursos pode-se desempenhar cálculos aritméticos, algébricos e utilizar múltiplas representações gráficas de objetos matemáticos.[br]O projeto do software GeoGebra foi idealizado por Markus Hohenwarter da Universidade de Salzburgo, onde atua como um de seus principais desenvolvedores em conjunto com Yves Kreis da Universidade de Luxemburgo.[br]O GeoGebra está disponível em múltiplas plataformas, e seus desenvolvedores permitem o seu download gratuito.[/justify]
[justify]O GeoGebra possui uma interface simples e organizada, sendo constituída de uma janela gráfica, subdividida em: área de trabalho, janela algébrica e campo de entrada, conforme pode-se observar na Figura 1. A Barra de Menus fornece as opções para o usuário administrar as configurações pessoais, e salvar projeto.[br][/justify]
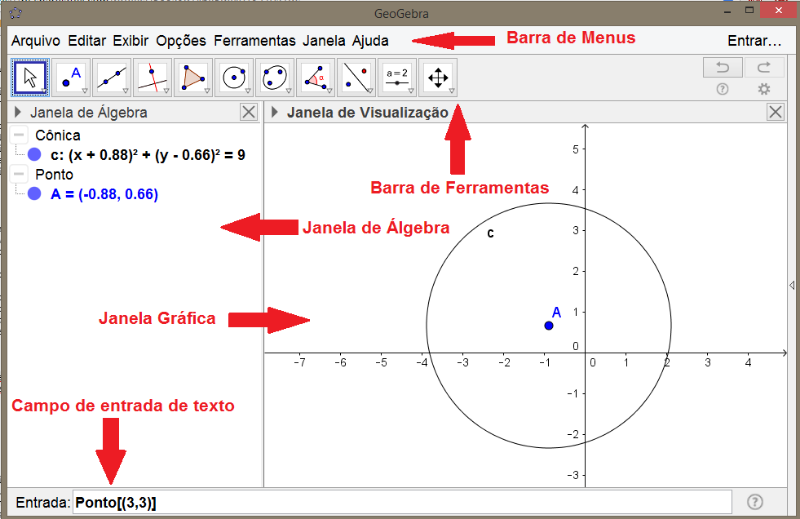
[size=200] Figura 1[/size]
[justify]A Janela de Álgebra é a região destinada a expor as coordenadas, medidas, equações e outras características dos objetos. O campo de entrada de texto é o espaço reservado para a digitação dos comandos, que determinam os objetos a serem construídos.[br]Na Barra de Ferramentas é onde se encontram todas as ferramentas utilizáveis, tais como pontos, retas e figuras geométricas.[/justify]
[justify][/justify][b][u]1) Circunferência trigonométrica[/u][/b][br][br]Nesta atividade vamos abordar como construir uma circunferência trigonométrica no GeoGebra. Para isso, vamos ao passo a passo.[br][br][b]1. [/b] Para construir o círculo digite na caixa de entrada: [i]círculo[(0,0),1] [/i][br][br][b]2. [/b] Agora iremos construir os segmentos que serão os eixos com círculo trigonométrico, para isso digite na caixa de entrada: [i]segmento[(-1.5,0),(1.5,0)][/i]. Depois, para construir o segundo segmento digite: segmento[i][(0,-1.5),(0,1.5)][/i][b]3. [/b]Oculte os eixos.[br][br][b]4. [/b]Obtenha o centro da circunferência, e chamemos o ponto de [i]O[/i], para isso digite : [i]O=(0,0)[/i].[br][br][b]5. [/b]Crie um ponto sobre a circunferência utilizando o recurso ponto sobre objeto, e chame este ponto de [i]A[/i] .[br][br][b]6.[/b] Crie o ponto [i]B[/i] , para isso digite : [i]B=(1,0)[/i][br][br][b]7.[/b] Crie uma semirreta com origem em [i]O[/i] e passando por [i]A[/i].[br][br][b]8. [/b]Criar um arco com centro em [i]O[/i], e as extremidades em [i]B[/i] e [i]A.[/i][br][br][b]9.[/b] Altere as configurações do arco mudando sua cor para vermelho e a espessura da linha um pouco mais grossa.[br][br][b]10.[/b] Ache o ponto [i]C[/i], sobre o eixo [i]x[/i], tal que [i]C[/i] é a projeção ortogonal de [i]A[/i] sobre o eixo [i]x[/i]. Para isso, digite: [i]C=(x(A),0)[/i].[br][br][b]11.[/b] Trace os segmentos [i]AC[/i] e [i]OC.[/i][br][br][b]12. [/b] Mude a cor dos dois segmentos criados acima em verde e azul respectivamente. Em seguida deixe a espessura a linha em 7.[br][br][b]13. [/b] Trace o ângulo [i]BÔA e[/i] omita o rótulo do ângulo. [br] [br][br]Agora responda, como obter o seno, cosseno e tangente do ângulo [i]BÔA[/i] em função dos lados do triângulo [br][i]AOC[/i].
[justify][b][u]2) Obtendo uma Função trigonométrica em função do Círculo trigonométrico.[/u][/b][br]Para fazer a construção, siga os passos a seguir.[br][br][b]1. [/b]Primeiro, abra uma segunda janela de visualização no arquivo do exercícios anterior, no menu[br]exibir.[br][br][b]2.[/b] Clique com botão direito do mouse na 2 janela e vá em “Janela de Visualização”. Na barra básico desmarque a opção “Exibir coordenadas do Mouse”. Na barra Eixo [i]x[/i], vá na opção distância e altere para [math]\frac{\pi}{2}[/math] [br]. Na barra Eixo [i]y[/i], fixe a distância como 1.[br][br][b]3. [/b]Na janela de visualização 2, construa um ponto [i]E[/i], para isso digite [i]:E=(e,0).[/i] Observe que [i]e [/i]é o tamanho do arco AB.[br][br][b]4. [/b]Vamos construir o segmento, OE, para isso digite [i]: segmento[O,E][/i]. Faça com que ele seja visível na janela de visualização 2. Copie o estilo do arco AB no segmento OE.[br][br][b]5. [/b]Crie o ponto [i]F[/i], para isso digite : [i]F=(e,x(C))[/i][br][br][b]6.[/b] Habilite o rastro do ponto F.[br][br][br]O rasto obtido é o gráfico da função [math]f\left(x\right)=cos\left(x\right)[/math].[br][br]Agora faça de forma similar, a construção da função [math]g\left(x\right)=sen\left(x\right)[/math].[br][br]Por fim, explique como essa construção pode auxiliar a introdução da matéria função trigonométrica em uma turma do 2º ano do ensino médio.[br][/justify]

