Integrated Math 2
GeoGebra materials used in teaching Integrated Math 2 (9th grade). Sequence and materials adapted from Mathematics Vision Project, Secondary 2 (http://www.mathematicsvisionproject.org/) with some help from EngageNY Algebra 1,2 and Geometry curricula (https://www.engageny.org)
Tabla de Contenidos
- Unit 1: Quadratic Functions
- Unit 2: Quadratic Expressions
- Unit 3: Quadratic Equations
- Unit 4: Features of Functions
- Unit 5: Geometric Figures
- Conjectures & Proof
- Unit 6: Similarity and Trigonometry
- Triangle Dilations
- IM2.6.1 Dilations
- IM2.6.1 Summary Task
- IM2.6.2: Side Splitter
- IM2.6.2 Exit Ticket
- IM2.6.3 Proving Conjectures
- IM2.6.3 Exit Ticket
- IM2.6.4 Big Diagram
- IM2.6.5 Exit ticket
- IM2.6.6 Pythagoras by proportions
- IM2.6.6 Exit ticket
- IM2.6.7 Similar right triangles 1
- IM2.6.7 Similar right triangles 2
- IM2.6.7 SRT3: SOHCAHTOA
- IM2.6.7 Exit Ticket
- IM2.6.8 Examine SOHCAHTOA
- IM2.6.8 Exit Ticket
- IM2.6.9 Solving Right Triangles
- IM2.6.9 Exit Ticket
- IM2.6.10 Exit Ticket
- IM2.6 Review 1: Similarity and angle relationships
- IM2.6 Review 2: Trigonometry
- IM2.6.3.1
- IM2.6.3.2
- IM2.6.3.3
- IM2.6.3.4
- Unit 7: Geometric Circles
- IM2.7 T1: Circle Basics
- IM2.7 T2: Centers of Rotation
- IM2.7 T3 Centers of Rotation 2
- IM2.7 T4 Chord Theorem
- IM2.7 T5 Inscribed Triangles
- IM2.7 T6 Cyclic Quadrilaterals
- IM2.7 T7: Inscribed Triangles, Circumscribed Angles
- IM2.7 T8 Angles formed by Secants (outside)
- IM2.7 T9: A special inscribed (?) angle
- IM2.7 inscribe
- Unit 8: Circles and Conics
- Unit 9: Probability
- IM2.9.1 TB or not TB?
- IM2.9.1 Exit Ticket
- IM2.9.2 Exit Ticket
- IM2.9.3 Warm Up
- IM2.9.3 Fried Freddy's
- IM2.9.3 Exit Ticket
- IM2.9.5 Exit Ticket
- IM2.9.6 Independence 1
- IM2.9.6 Independence 2
- IM2.9.6 Exit Ticket
Conjectures & Proof
Construct the midpoint for one of the sides of the triangle by pressing the "midpoint" button then clicking on the side for which you want a midpoint. Then rotate the triangle about that midpoint by clicking the "rotate about point" button, clicking the triangle you want to rotate, clicking the midpoint around which you want to rotate the triangle, and entering the letter name of the next unused slider (if it is your first rotation, enter "a"). Then, after clicking the "cursor" tool, drag the slider you just entered to see your triangle rotate. Label and color the angles of your new triangle using the "angle" tool by clicking the three vertices of the triangle. The first point you click will have a blue angle label, the second you click will have a red angle label, and the third will have a yellow angle label. Repeat this process to answer the questions at the bottom of this page.
Conjectures & Proof
1. Display a sequence of triangles to illustrate that alternate interior angles formed by parallel lines cut by a transversal are congruent.[br][br]2. Display a sequence of triangles so that the perimeter of the final figure is a pentagon, then use the display to determine the sum of the interior angles of the pentagon.
Triangle Dilations
Use the rubber band stretcher to dilate the given triangle by a factor of 3 centered at point M. Also use the rubber band stretcher to dilate the give triangle by a factor of 1/2 centered at N. Can you use the rubber band stretcher to show that the larger of the two new triangles formed is a dilation of the smaller? (See Mathematics Vision Project, Secondary Math II, task 6.2 for details.)
Triangle Dilations
IM2.7 T1: Circle Basics
Vocabulary and Checkboxes
For this task, you'll need to construct a circle with checkboxes showing the different parts (follow [url=http://www.geogebra.org/material/simple/id/3529]this link[/url] for an example). The words you need to include checkboxes for are:[br]Chord[br]Secant line[br]Tangent line[br]Diameter[br]Radius[br]Arc[br]Sector[br]Circumference[br]Central angle[br]Inscribed angle[br]You may need to do some research to find out how to show some of these words.[br]You may want to use a separate GeoGebra window. If so, please make sure to save your construction under your account, and paste the link in the comments below this post.
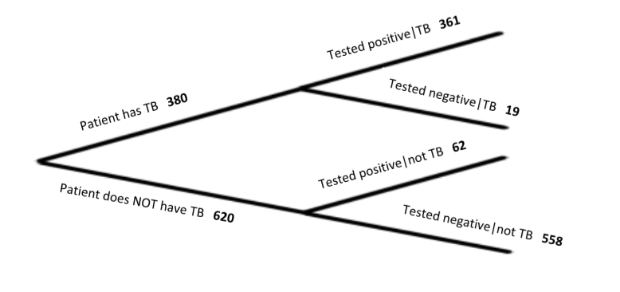
IM2.9.1 TB or not TB?
1. Different Representations
Tuberculosis (TB) can be tested in a variety of ways, including a skin test. If a person has tuberculosis antibodies, then they are considered to have TB. Above is a tree diagram representing data based on 1,000 people who have been given a skin test for tuberculosis. [b]Notation[/b]: the vertical line is a symbol for conditional probability, and is read as “given”. For example, “Tested positive[math]|[/math]TB” is read as “the person tested positive given that they had tuberculosis”.[br]Fill in the following two way table showing probabilities (decimals) of each situation.
2. Conditional Statements
Based on the information in the table above, write some conditional statements.Starters:[br]If a patient has TB, then…[br]If a patient tested negative for TB, then…[br]