Curiosités polygonales
Índice
- L'ennéagone de Voderberg
- Une construction d'un ennéagone de Voderberg
- Pavage du polygone régulier à 24 côtés
- Spirale de Voderberg
- Pavage d'un octodécagone
- Le cerf-volant de Tamvakis
- Le cerf-volant de Tamvakis
- Un golygone à 60°
- Un golygone à 60°
- Second golygone
- Le pentagone du Caire
- Le pentagone du Caire
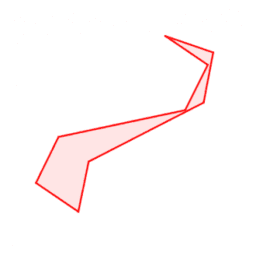
Une construction d'un ennéagone de Voderberg
|
Polygone à 9 côtés découvert par Heinz Voderberg en 1936. Il pave le plan de manière périodique, mais aussi en formant une spirale. Cette construction est obtenue uniquement en reliant des sommets d'un polygone régulier à 24 côtés, de centre O : 3-13 coupe 4-14 en E, 7-21 en C et 2-12 en F. 6-18 coupe 2-14 en O et 4-14 en D, 2-16 coupe 3-21 en B, 1-15 coupe 2-20 en A. |
|
|
|
L'angle au centre du polygone est égal à 15° (360°/24). Faire tourner de 15° autour de O une droite reliant deux sommets revient à ajouter 1 aux numéros de ces points (modulo 24). Exemple : l'image de 1-15 par la rotation de centre O et d'angle 15° est 2-16. Cette propriété permet de montrer que la chaîne de segments OEDB2 est l'image de OFCA1 par cette même rotation. On peut aussi établir l'égalité de certaines longueurs, comme par exemple 1-A = 2-B. |
Le cerf-volant de Tamvakis
En 1987, Nikolaos Tamvakis, de l'académie navale hellénique, découvrit une figure très spéciale.[br]En effet, parmi tous les quadrilatères dont la distance maximale entre deux sommets est égale à 1, c'est celui de Tamvakis qui a le plus grand périmètre.[br]Voici comment on peut construire ce quadrilatère :
voir [i]Pour La Science[/i], n°381, Juillet 2009.
Tamvakis4
Un golygone à 60°
|
Cet ennéagone a été découvert en 1990 par Lee Sallows. Les longueurs de ses côtés sont, dans lʼordre, les entiers de 1 à 9. Et chacun de ses angles aigus vaut 60°. Un exercice de construction assez plaisant à faire en classe de sixième. Avec au passage un mini-défi : le dernier segment tracé doit rejoindre le premier ! En quatrième on peut calculer l'aire du polygone à partir de celle d'un triangle équilatéral de côté 1. |
|
|
|
Voir [i]New Pathways in Serial Isogons[/i], Lee C.F. Sallows, 1992 [url]http://leesallows.com/files/New%20Pathways.pdf[/url] |
Le pentagone du Caire
Ce pentagone apparaît fréquemment dans les rues du Caire, la capitale de l'Egypte. [br]Quatre d'entre eux peuvent être assembler pour former un hexagone et ainsi recouvrir tout le plan. [br]Ce recouvrement s'appelle [b]le pavage du Caire[/b].