Differentialrechnung

John Flath, Mar 1, 2017

Table of Contents

  1. Funktionen
    1. Exponential Functions: Graphs
    2. Exponential Functions (Graph & Equation Anatomy)
    3. Domain & Range: Illustrated
  2. Sekante Tangente
    1. Differentiation from first principles
    2. Differential calculus - first principles
  3. Ableitung Sinus und Cosinus
    1. Ableitung der Sinusfunktion
    2. Ableitung der Cosinusfunktion
    3. Sine & Cosine of a Sum: Discovery
    4. Unit Circle and Sine Graph
  4. Optimierung
  5. Zweite Ableitung
    1. Zusammenhang von Funktion und Ableitung
    2. Zusammenhänge erste und zweite Ableitung
  6. Kurvendiskussion

1.

Funktionen

  • 1. Exponential Functions: Graphs
  • 2. Exponential Functions (Graph & Equation Anatomy)
  • 3. Domain & Range: Illustrated

1.1.

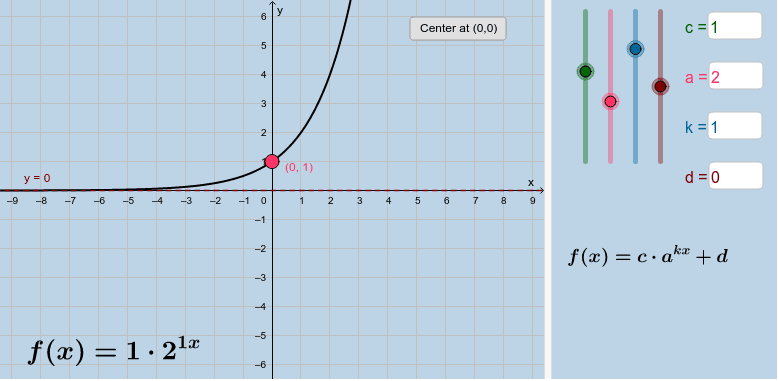
Exponential Functions: Graphs

The following applet displays the graph of the exponential function [math]f\left(x\right)=c\cdot a^{kx}+d[/math]. [br]Interact with the applet below for a few minutes, then answer the questions that follow.
[b][color=#000000]Questions:[/color][/b][br][br][color=#000000]1) How does the parameter [/color][color=#cc0000][b]a[/b][/color] [color=#000000]affect the graph of the exponential function? Explain. [br] What happens if [/color][color=#cc0000][b]a > 1[/b][/color][color=#000000] and [/color][color=#1e84cc][b]k > 0[/b][/color][color=#000000]? What happens if [/color][color=#cc0000][b]a < 1[/b][/color][color=#000000] and [/color][color=#1e84cc][b]k > 0[/b][/color][color=#000000]? [br][br][/color][color=#000000]2) How does the parameter [/color][b][color=#1e84cc]k[/color][/b][color=#000000] affect the graph? Explain. [br] If you need a hint, refer back to [url=https://www.geogebra.org/m/HJvZSUna]this worksheet[/url]. [br][br][/color][color=#000000]3) What does the parameter [/color][color=#980000][b]d[/b][/color][color=#000000] do the graph? Explain. [br][br][/color][color=#000000]4) Suppose [/color][color=#cc0000][b]a < 1[/b][/color][color=#000000]. [br] Given this constraint, is it possible to get the graph of this exponential function to look the way it does[br] when [/color][color=#cc0000][b]a > 1[/b][/color][color=#000000] and [/color][color=#1e84cc][b]k > 0[/b][/color][color=#000000]? Explain. [/color]
– Tim Brzezinski

1.2.

–

1.3.

–

2.

Sekante Tangente

  • 1. Differentiation from first principles
  • 2. Differential calculus - first principles

2.1.

Differentiation from first principles

Differentiation from first principles
What happens to the gradient of the chord line as PN approaches 0?
– Mark Willis

2.2.

–

3.

Ableitung Sinus und Cosinus

  • 1. Ableitung der Sinusfunktion
  • 2. Ableitung der Cosinusfunktion
  • 3. Sine & Cosine of a Sum: Discovery
  • 4. Unit Circle and Sine Graph

3.1.

Ableitung der Sinusfunktion

– Hubert Pöchtrager

3.2.

–

3.3.

–

3.4.

–

4.

Optimierung


    This chapter does not contain any resources yet.

5.

Zweite Ableitung

  • 1. Zusammenhang von Funktion und Ableitung
  • 2. Zusammenhänge erste und zweite Ableitung

5.1.

Zusammenhang von Funktion und Ableitung

Zusammenhang von Funktion und Ableitung
– thuewe

5.2.

–

6.

Kurvendiskussion


    This chapter does not contain any resources yet.

Information