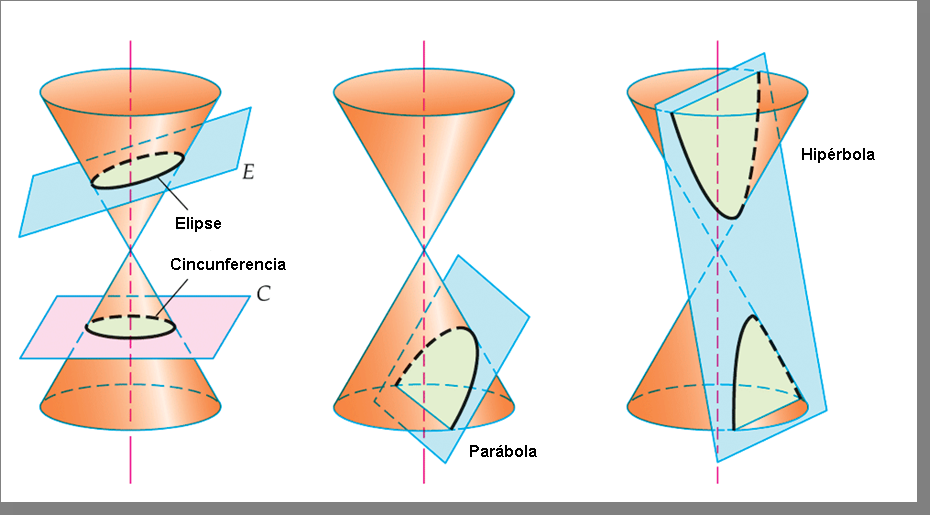
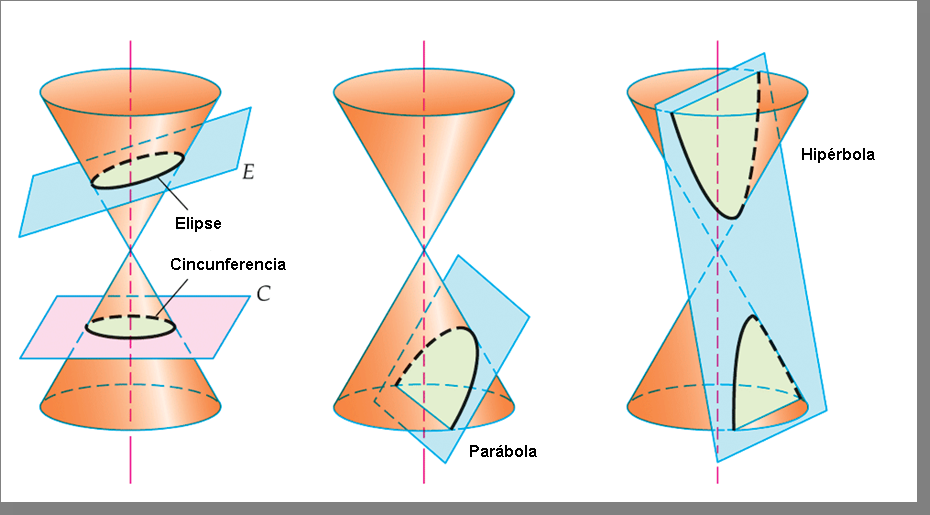
[justify] Como todo conhecimento científico, as idéias Matemáticas passam por um processo evolutivo incorporando mudanças, sendo tratadas com novas ferramentas e métodos os quais, muitas vezes, lhes permitem um incremento no seu desenvolvimento.[br] As [i]seções cônicas[/i] são curvas obtidas pela interseção de um cone circular reto de duas folhas com um plano. Exposições gerais sobre as seções cônicas são conhecidas antes da época de Euclides (±325-265 a.C.) e existe uma diversidade de definições para elas, cuja equivalência é mostrada na Geometria Elementar. Atualmente, as mais usuais referem-se à [i]propriedade foco - diretriz[/i] dessas curvas, porém, em seu célebre tratado sobre as seções cônicas, Apolônio de Perga (± 262-190 a.C.) não mencionou essa propriedade e não existia um conceito numérico que correspondia ao que chamamos de excentricidade. Coube a Pierre de Fermat a descoberta de que as seções cônicas podem ser expressas por equações do segundo grau nas coordenadas (x,y).[br] Neste trabalho, mostramos que uma seção cônica é uma curva cuja equação cartesiana é do segundo grau, e inversamente, toda curva cuja equação é do segundo grau pode ser obtida a partir da interseção de um cone circular reto de duas folhas com um plano. Por essa razão, as curvas cujas equações são do segundo grau são chamadas de seções cônicas, ou simplesmente de [i]cônicas[/i]. O objetivo deste trabalho é incentivar o aluno de geometria analítica para o estudo deste belo e rico tópico de Geometria, que são as seções cônicas e suas propriedades. Mostramos que as seções cônicas podem ser definidas e geradas de várias maneiras, sendo elas matematicamente equivalentes, com isso estaremos oferecendo uma rara oportunidade para mesclar geometria analítica com Geometria Espacial (Euclidiana), lugares geométricos, junto com uma coletânea de resultados por si só interessantes. Além disso, esperamos que a importância das seções cônicas para a Matemática pura e aplicada seja estabelecida ao apresentarmos as propriedades focais de suas tangentes e suas aplicações práticas. Uma breve introdução histórica sobre as cônicas é apresentada. Finalmente, observamos que o pré-requisito para este estudo consiste apenas de alguns conceitos básicos de Geometria Euclidiana e, sempre que possível, iremos utilizar os recursos do software de [i]geometria dinâmica [b]GEOGEBRA[/b] [/i]como auxílio na ilustração de conceitos e na aprendizagem.[br][size=50][color=#0000ff]Fonte: www.sato.prof.ufu.br/Conicas/node1.html acessado em: 20/09/17[/color][/size][/justify]

 [justify] Tratados sobre as seções cônicas são conhecidos antes da época de Euclides (± 325-265 a.C.). E, associado à história dessas curvas, temos Apolônio que nasceu na cidade de Perga, região da Panfília (atualmente Turquia) por volta de 262 a.C. e viveu, aproximadamente, até 190 a.C.[br] Apolônio foi contemporâneo e rival de Arquimedes que viveu, aproximadamente, entre 287 a.C. e 212 a.C. e, juntamente com Euclides, formam a tríade considerada como sendo a dos maiores matemáticos gregos da antiguidade. Apolônio estudou com os discípulos de Euclides em Alexandria e foi astrônomo notável, talvez ele, e não Euclides, mereceu dos antigos o adjetivo de "o grande Geômetra ". A maior parte das obras de Apolônio desapareceu. O que sabemos dessas obras perdidas devemos a Pappus de Alexandria (séc IV a.C.). Sua obra prima é [b]Seções Cônicas [/b]composta por 8 volumes (aproximadamente 400 proposições!). Da obra original sobreviveram 7 volumes, sendo 4 escritos em grego e 3 traduzidos para o árabe por Thabit Ibn Qurra (826 a 901) no séc. IX.. Os três primeiros volumes são baseados em trabalhos de Euclides e o oitavo volume foi, infelizmente, perdido. Em 1.710, Edmund Halley traduziu os sete volumes sobreviventes de Secções Cônicas para o latim e todas as demais traduções para as línguas modernas foram feitas a partir da tradução de Halley.[br] Os precursores de Apolônio no estudo das cônicas foram Manaecmo, Aristeu e o próprio Euclides. Nesse período, elas eram obtidas seccionando um cone circular reto de uma folha com um plano perpendicular a uma geratriz do cone, obtendo três tipos distintos de curvas, conforme a seção meridiana do cone fosse um ângulo agudo, um ângulo reto ou um ângulo obtuso.[br] Apolônio foi o matemático que mais estudou e desenvolveu as seções cônicas na antiguidade. Suas contribuições foram: ter conseguido gerar todas as cônicas de um único cone de duas folhas, simplesmente variando a inclinação do plano de interseção; ter introduzido os nomes elipse e hipérbole e ter estudado as retas tangentes e normais a uma cônica.[br][color=#0000ff][size=50]Fonte: http://www.sato.prof.ufu.br/Conicas/node2.html acessado em: 20/09/17[/size][/color][/justify]