Mathematik in der 8. Jahrgangsstufe
Gesammelte Interaktivitäten zur Mathematik in der 8. Jahrgangsstufe.
Índice analítico
- Zuordnungen
- Entstehung eines Graphen
- Flächeninhalt des Kreises
- Näherung des Kreisflächeninhalts durch Umformen
- Approximation des Kreisflächeninhalts
- Kreisflächeninhalt und -umfang
- Lineare Funktionen
- Betrachtungen zur Steigung linearer Funktionen
- Funktion zur Nullstelle finden
- Black-Box-Funktion
- Senkrechte Geraden
- Finden der Regressionsgeraden
- Strahlensätze und Ähnlichkeit
- Einstieg Strahlensatz
- Die V-Figur
- Die Koch-Kurve
Entstehung eines Graphen
Näherung des Kreisflächeninhalts durch Umformen
Erkunde den Kreisflächeninhalt mit Hilfe der unten stehenden Interaktivität.
[size=85]Diese Interaktivität ist lediglich eine Übersetzung des [url=https://www.geogebra.org/m/fyqAUV22]hervorragenden Applets [/url]von [url=https://www.geogebra.org/orchiming]Anthony C.M. OR[/url] vom GeoGebra-Institut Hong Kong. Ihm gebührt jeglicher Dank.[br][br]This is merely a translation of the [url=https://www.geogebra.org/m/fyqAUV22]extraordinary applet[/url] by [url=https://www.geogebra.org/orchiming]Anthony C.M. OR[/url] from the GeoGebra Institute of Hong Kong. All credit goes to him.[br][/size]
Betrachtungen zur Steigung linearer Funktionen
[size=150][b]Bevor du loslegst:[br][/b][list][*][size=100]Schlage dein Schulheft auf, notiere das Datum und die Überschrift "Lineare Funktionen am Rechner".[/size][br][/*][size=100][*]Schreibe darunter die Überschrift von oben. [/*][*]Bearbeite dann die Aufgaben unten.[br][/*][/size][/list][/size]
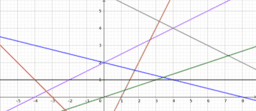
[size=100][size=150][b]Aufgaben[/b][br][/size][br][/size]Betrachte die Interaktivität unten. Hier kannst du mit Hilfe der Textfelder Steigung und y-Achsenabschnitt der Funktion f einstellen. Ihr Graph ist die blau gezeichnete Gerade.[br][br][b]Aufgabe 1:[/b][br]a) Für welche Werte von m steigt die Gerade? Für welche m fällt sie?[br]b) Für welche Werte von m steigt die Gerade steiler als die Winkelhalbierende des 1. und 3. Quadranten? Für welche Werte verläuft sie flacher?[br]c) Für welche Werte von m fällt die Gerade steiler als die Winkelhalbierende des 2. und 4. Quadranten? Für welche Werte verläuft sie flacher?[br]Notiere dir für die Teilaufgaben oben jeweils die Werte in dein Heft.
Einstieg Strahlensatz
Bevor du loslegst:
[list][*][size=100]Schlage dein Schulheft auf, notiere das Datum und die Überschrift "6.2 Strahlensätze: Die V-Figur".[/size][/*][size=100][*]Bearbeite dann die Aufgaben unten. Du kannst mit deinem Nachbarn oder deiner Nachbarin zusammenarbeiten.[/*][/size][/list]
Einstieg
Unten siehst du eine Experimentierumgebung, die das Laserpointer-Experiment simuliert.[br][list][*]Stelle eine bestimmte Genauigkeit ein (oder lasse die, die schon eingestellt ist).[br][/*][*]Versuche mit den beiden Punkten auf der x-Achse die Trefferbereiche so einzustellen, dass der für die weite Entfernung genau doppelt so groß ist wie der für die kurze.[/*][*]Vergleiche nun die Abstände des Ziels in der kurzen und der weiten Entfernung. Was fällt auf? Notiere dir deine Beobachtung in dem Textfeld unterhalb der Experimentierumgebung.[/*][*]Mache dann mit den weiteren Fragen unter der Experimentierumgebung weiter.[/*][/list]
Experimentierumgebung
Frage 1
Welcher Zusammenhang besteht zwischen den Abständen von nahem und weitem Ziel, wenn der weit entfernte Trefferbereich genau doppelt so groß ist wie der nahe?
Frage 2
Was passiert umgekehrt mit den Trefferbereichen, wenn das entfernte Ziel dreimal so weit entfernt ist wie das nahe? Viermal? 1,5-mal? Notiere deine Beobachtungen unterhalb:
Wie geht's weiter?
Wenn du schon so weit bist: Prima! Warte kurz, bis die Anderen auch so weit sind und wir unsere Ergebnisse sammeln können.