-
GeoGebra and Mathematics Educacion
-
1. The aim of this paper
- Jogo dos Pontos
- Teorema Fundamental do Cálculo
-
2. Lines of research
- Objetos de Aprendizagem construídos com GeoGebra
-
3. Didactic Transposition of Knowledge
-
4. Overview of what was done
-
5. Non Euclidean Geometry
- Elliptic Triangle
-
6. Experimental study
-
7. Approach of this Research
-
8. Methodology
-
9. Results
GeoGebra and Mathematics Educacion
Celina Abar, 23.05.2015

This GeoGebra Book presents the work developed for the GeoGebra 2015 Global Gathering in Linz of the 15 July 17, 2015. [b]Celina A. A. P. Abar [/b] [i]Postgraduate Program Studies in Mathematics Education GeoGebra Institute of São Paulo Pontifical Catholic University - São Paulo- Brazil[/i]
Inhaltsverzeichnis
- The aim of this paper
- Jogo dos Pontos
- Teorema Fundamental do Cálculo
- Lines of research
- Objetos de Aprendizagem construídos com GeoGebra
- Didactic Transposition of Knowledge
- Overview of what was done
- Non Euclidean Geometry
- Elliptic Triangle
- Experimental study
- Approach of this Research
- Methodology
- Results
The aim of this paper
The aim of this paper is to present the researches projects of the group “Technologies and Expression Media for Mathematics – TecMEM”, of the Post-Graduate Studies in Mathematics Education at PUC/SP and São Paulo Institute of GeoGebra. [url]http://www.pucsp.br/tecmem/OAs.htm[/url] Many studies of this group were developed with the use of GeoGebra, which has been an important resource for teaching and learning of mathematics. Each one used different theoretical and methodological supports and presented considerations about use GeoGebra, the goals of each author, and the results obtained. All these researches show the knowledge of the carried out, specifically those using GeoGebra, the postgraduate production obtained, which aspects and dimensions were highlighted and favored, justifying the significance of using GeoGebra in Mathematics Education. All researches show the educational choice to use GeoGebra in Mathematics Education. [url]http://www.pucsp.br/tecmem/Andre/GeoGebra-Andre/inicio.html[/url]
-
1. Jogo dos Pontos
-
2. Teorema Fundamental do Cálculo
Jogo dos Pontos
Lines of research
One of the lines of research aims to understand the difficulties in the practice of mathematics teachers. The elementary school teachers see the university as a service provider which can assist their teaching and whose production is not restricted to the shelves of university libraries. These difficulties show that, in order for a teacher to use a technological tool as support to teach mathematics, it is first recommended to determine what goals he/she intends to reach, which type of mathematical knowledge he/she intends to provide his/her students with, and which technological tool can help him/her to reach such goal.
-
1. Objetos de Aprendizagem construídos com GeoGebra
Objetos de Aprendizagem construídos com GeoGebra
Didactic Transposition of Knowledge
[b]The difficulties relate to the didactic transposition of knowledge to teach and the possibilities offered by GeoGebra in order to create educational strategies to enhance and streamline the construction process of mathematical knowledge by teachers and students. [/b]
Dieses Kapitel enthält noch keine Materialien
Overview of what was done
Here we present an overview of what was done to collaborate with the education and mathematics from the use of GeoGebra that has been an important resource for teaching and learning. [url]http://www.pucsp.br/tecmem/sergio_alencar.pdf[/url]
Dieses Kapitel enthält noch keine Materialien
Non Euclidean Geometry
This researche is about Non-Euclidean Geometry. In case of Eliptic Geometry we use learning scenarios available on the internet and built with GeoGebra, to offer an alternative of continuing training for Mathematics teachers. [b]Possible Negations of the Parallel Postulate of Euclidean Geometry[/b] [i]For a point outside a line there is more than one parallel, what justifies the Hyperbolic Geometry.[/i] • Felix Klein Model: • Model of Henri Poincaré (1854-1912) • Disco de Poincaré: similar to the Klein model of Elliptic Geometry. • A three-dimensional model obtained by rotating a curve-directivity tractrix [b]For a point outside a line does not exist any parallel. In this case we have the Spherical Geometry and Elliptic Geometry;[/b] In the universe of Elliptic Geometry are part the Projective geometries, Stereographic and Hyperspherical or Spherical Surface [url]http://geogebratube.org/student/m166789 [/url]
-
1. Elliptic Triangle
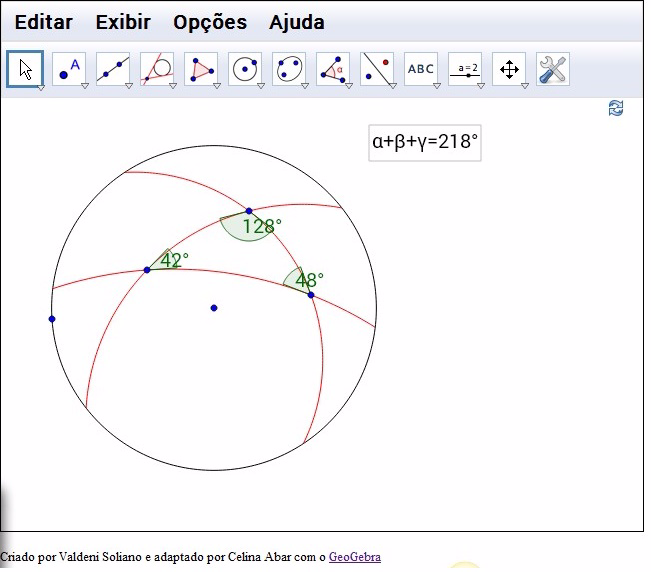
Elliptic Triangle
Elliptic Triangle

Methodology
The methodology used is the Design Experiments that allows a formative evaluation to refine educational projects. The survey used the Elliptical Geometry model similar to Poincaré model for Hyperbolic Geometry. In this model: • The plan is a unit circle, including points of the circle. • The "points" are the Euclidean points inside the unit circle, as well as the pairs of antipodal points on the circle are identified. • The "straight" are or diameters of circle or arcs of Euclidean circles that intersect the circumference of the unit circle in the extremities of a diameter. The activities in this first step and used in this work had as objective to identify factors that could hinder, on the part of teachers, knowledge and understanding of the Non-Euclidean Geometry, in particular Elliptic Geometry. [url]http://www.pucsp.br/tecmem/OAs/reta_eliptica.html[/url]
Dieses Kapitel enthält noch keine Materialien
Results
The results reveal a change of attitudes and values in teachers and show that some aspects of geometry were learned and became institutionalized knowledge, revealing that the use of technologies, as mediators in the learning process, may subsidize pedagogical strategies to teach and learn Mathematics. The evaluation of the proposal has been well received by teachers, who considered the scenario available, suitable for the initial understanding of Elliptic Geometry. They observed that the use and the lack of possibilities of GeoGebra can interfere with achievement of goals and, also, it is necessary a time more suitable for the development of the activities.
Dieses Kapitel enthält noch keine Materialien