Planetary Motion in GeoGebra
Table of Contents
- Introduction
- University of South Bohemia in České Budějovice
- Annotation
- Inspiration
- Richard Feynman
- Feynman's lectures on physics
- Feynman's lost lecture
- Objectives
- Planetary motion in GeoGebra
- Educational benefits
- Respective Physical Laws
- Kepler's laws of planetary motion
- Newton's laws of motion and gravity
- Numerical approach
- Numerical analysis of planetary motion
- Geometric approach
- Second Kepler's law: The law of equal areas
- First Kepler's law: The law of ellipses
- Feynman's proof of the law of ellipses
- References
- References
University of South Bohemia in České Budějovice
[b][size=150]University of South Bohemia in České Budějovice[/size][/b][b][size=150], Faculty of Education[/size][/b][br] [size=150][url=http://www.jcu.cz/?set_language=en]www.jcu.cz[/url][/size][br][br][size=150][b]GeoGebra Institute of České Budějovice[/b][br][url=http://home.pf.jcu.cz/~ggi/GeoGebra_Institut/Uvod.html]home.pf.jcu.cz/~ggi/GeoGebra_Institut/Uvod.html[/url][/size]
Richard Feynman
[size=150][b]Richard Feynman (1918 - 1988)[/b], American physicists and Nobel prize holder, published two contributions on the derivation of[b] Kepler's laws[/b] of planetary motions applying [b]Newton's laws[/b] of motion and gravity (this method was used also by Newton himself to prove the correctnes of his assumptions):[br][br]Feynman's Lectures on Physics (three volume book, 1963) - the numerical approach [br][br]The Motion of Planets around the Sun (guest lecture, 1964) - geometric approach[br][br][br][/size]
Planetary motion in GeoGebra
[size=150]The aim of this presentation is to show the use of GeoGebra to illustrate the base idea of geometric proof of the 1[sup]st[/sup] (law of ellipses) and 2[sup]nd[/sup] (law of equal areas) Kepler’s laws by Richard Feynman.[br][br]My earlier work on the same topic, dealing with the numerical model will also be mentioned.[/size][br][br][size=150][b]GeoGebra provides an environment suitable for the realization of both numerical and geometric models of planetary motion.[/b][/size]
Kepler's laws of planetary motion
[size=150]The motion of planets is describedby the three Kepler’s laws, which belong to the usual secondary school curriculum. [br][br][b]Johannes Kepler (1571–1630)[/b], German mathematician and astronomer, whose life was closely connected to Graz and Linz in Austria, and Praha in Bohemia, published the three laws over a period of time in two books. [br][br]He based his findings on observations of the Danish astronomer [b]Tycho Brahe (1546–1601)[/b].[br][br]First, in 1609 in [i]Astronomia nova[/i], Kepler published two statements that are known as his 1[sup]st [/sup]and 2[sup]nd[/sup] laws of planetary motion.[br][br][/size][list][*][size=150] [i]Orbits of all the planets are ellipses with the Sun at one focus ([size=150]Kepler’s 1[sup]st[/sup] law, the law of ellipses).[/size][/i][/size][/*][/list][list][*][size=150] [i]A line segment from the Sun to a planet sweeps out equal areas in equal time ([size=150]Kepler’s 2[sup]nd[/sup] law, the law of equal areas)[/size].[/i][/size][/*][/list][size=150][br]Then, in 1619 in [i]Harmonices mundi[/i], he added the third law. [br][br][/size][list][*][size=150][b] [/b][i]The orbital period of a planet is proportional to the three-halves power of the size of the semi–major axis of its orbit ([size=150]Kepler’s 3[sup]rd[/sup] law, the law of harmonies)[/size].[/i][/size][/*][/list]
Numerical analysis of planetary motion
[size=150]The numerical approach to the derivation of Kepler’s law from Newton’s laws (of motion and gravity) was introduced in the book [i]Feynman’s Lectures on Physics[/i] (three volume book, which was first published in 1963).[br][br]This method consists of the gradual numerical computation of coordinates of a planet moving in the gravitational field of the Earth, entering them in the table and their subsequent graphical representation.[br] [br]GeoGebra has been proved as the ideal environment for the implementation of this method due to the combination of numerical calculations, tables and graphical view required.[br][br]A contribution on this topic was presented at the [url=https://wiki.geogebra.org/en/GeoGebra_Conference_2011]GeoGebra Conference 2011[/url] in Hagenberg. [br][br]A corresponding paper Hašek, R. [url=http://www.geogebrajournal.com/index.php/ggbj/article/view/12/15]Numerical analysis of a planar motion: GeoGebra as a tool of investigation[/url], was published in the [url=http://www.geogebrajournal.com/index.php/ggbj/index]North American GeoGebra Journal[/url], Vol 1, No 1 (2012).[/size]
Second Kepler's law: The law of equal areas
[size=150][i][b]Planets sweep out equal areas in equal time.[/b][/i][br][br]The geometric proof of the second Kepler's law presented by R. Feynman corresponded to the proof which was published by Isaac Newton in his [i]Principia[/i] ([i]Philosophiæ Naturalis Principia Mathematica[/i] / [i]Mathematical Principles of Natural Philosophy[/i], 1697). [br][br]Feynman used almost an identical illustration to the original one by Newton:[/size]
[i]Illustration from: Newton's Principia: the mathematical principles of natural philosophy by Sir Isaac Newton; translated into English by Andrew Motte, New-York: Published by Daniel Adee, 1846.[/i]
[size=150]This geometric proof is based on the elementary properties of a triangle, particularly on the way of the computation of its area. [br] [br] [br][b]Exercise:[/b] [i]Given triangles SAB, SAC, SBC and SBD (D is movable along p) in the figure below so that B is the midpoint of the segment AC and p is parallel to SB. Determine the relations of areas of all the given triangles. Justify your claim.[/i][/size][br]
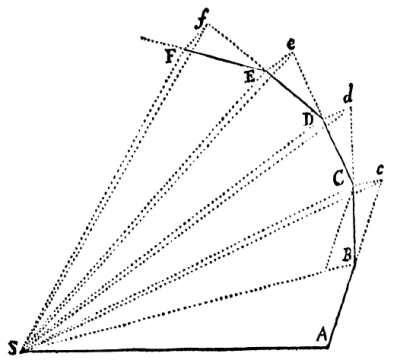
[size=150][b]Exercise: [/b][i]See the figure below. Points A, B, C,D and E are the successive positions of a planet in its orbit around the Sun (point S) at equal intervals of time. Then, due to the law of inertia |AB| = |Bc|, |BC| = |Cd| and |CD| = |De|. [br]In accordance with statement of the 2[sup]nd[/sup] Kepler's law (the law of equal areas) it follows that the areas of triangles SAB, SBC, SCD and SDE are equal. Prove it. You can do it gradually, using triangles SBc, SCd and SDe (be aware that cC, dD and eE are parallel to BS, CS and DS, respectively). [/i] [br][/size]
[size=150]The 2[sup]nd [/sup]Kepler’s law (the law of equal areas) appeared to be a consequence of the law of inertia (Newton’s first law) and the fact that changes in motion of planets are caused by the gravitational force directed toward the Sun.[br][br][b]What causes the elliptical shape of a planet's orbit?[/b][/size]
References
[size=150][size=150]Goodstein, [size=150][size=150]D. L.[/size][/size] and Goodstein, [size=150][size=150]J. R[/size][/size]. (1996) [/size][i]Feynman's Lost Lecture, The Motion of Planets around the Sun[/i], London: Vintage Books.[br][br]Feynman, R., Leighton, R. and Sands, M. (2005) [i]The Feynman Lectures on Physics[/i], 2[sup]nd[/sup] ed., Volume 1, Addison Wesley, USA. [br][br][/size]