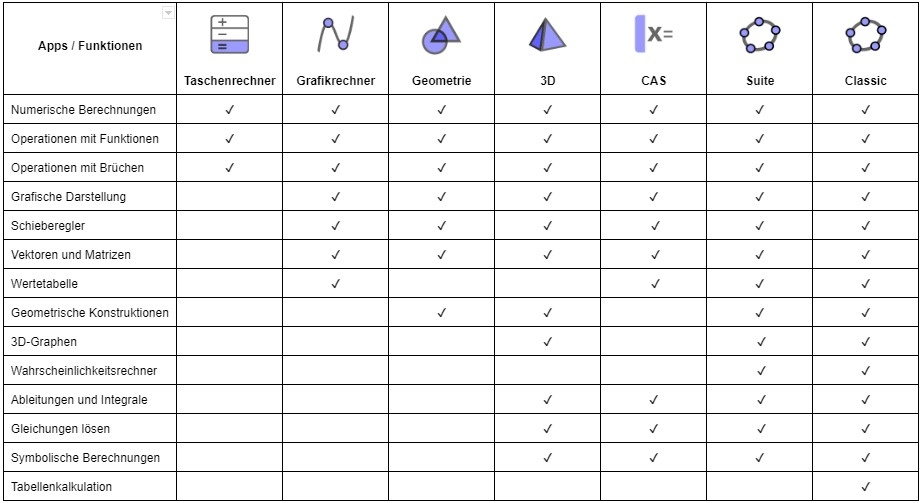
Vergleich der GeoGebra Mathe Apps
Mit unseren [i]GeoGebra Mathe Apps[/i] kannst du Funktionen, Geometrie, Algebra, Statistik und 3D auf eine neue und interaktive Weise erkunden und lernen.[br][list][*][url=http://www.geogebra.org/scientific]Taschenrechner[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafikrechner[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometrie[/url][br][/*][*][url=https://www.geogebra.org/calculator]Rechner Suite[/url][/*][*][url=https://www.geogebra.org/cas]CAS Rechner[/url][br][/*][*][url=https://www.geogebra.org/3d]3D Rechner[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Classic[/url][br][/*][/list]Die richtige App für dich ist die, die deinen eigenen Bedürfnissen entspricht und, wenn sie in Prüfungen verwendet wird, die Prüfungsbestimmungen für deine Region erfüllt. Die folgende Tabelle gibt einen Überblick darüber, welche Funktionen in welchen Apps verfügbar sind.

GeoGebra in Prüfungen
Wir glauben, dass die Schüler*innen davon profitieren, wenn sie im Unterricht, bei den Hausübungen und während Prüfungen genau dieselbe [i]GeoGebra [/i]App verwenden. Auf diese Weise erhalten sie die meiste Übung mit der App und können unsere Technologie daher in allen Situationen optimal nutzen. Aus diesem Grund haben wir unseren [i]GeoGebra Prüfungsmodus[/i] erstellt und ihn in jede unserer Apps eingefügt. Der [i]Prüfungsmodus [/i]sperrt mobile Geräte, sodass die Schüler*innen während einer Prüfung keine anderen Apps als [i]GeoGebra[/i] verwenden und mit diesen kommunizieren können. Dieser Ansatz wurde bereits von mehreren Bildungsministerien in mehreren Regionen erprobt und genehmigt. Erfahre mehr über die Verwendung von [url=https://www.geogebra.org/m/m97r7cd4][i]GeoGebra[/i] in Prüfungen[/url].[br][br]
Schnitt von Funktionen
Aufgabe
Erstelle eine lineare Funktion mit Schiebereglern und schneide diese mit einer quadratischen Funktion.[br][br]Erforsche die Konstruktion und lerne, wie du eine Funktion mit Parametern erstellst und wie du mit dem [i][url=https://www.geogebra.org/graphing]GeoGebra Grafikrechner[/url] [/i]zwei Funktionen schneiden kannst. Danach versuche es selbst, indem du die folgenden Anleitungen befolgst.
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1.[/td][td][/td][td]Gib die lineare Funktion [math]f(x)=a\cdot x+b[/math] in das [i]Eingabefeld[/i] ein. Es werden automatisch Schieberegler für die Variablen [i]a[/i] und [i]b[/i] erstellt.[/td][/tr][tr][td]2.[/td][td][/td][td]Aktiviere den [i]Sichtbarkeits-Button [/i]neben den Schiebereglern, um diese in der [i]Grafikansicht[/i] anzuzeigen.[br][/td][/tr][tr][td]3.[/td][td][/td][td]Ändere die Werte der Schieberegler für [i]a[/i] und [i]b[/i] und erforsche, wie sich der Graph von[i] f(x)[/i] ändert.[br][/td][/tr][tr][td]4.[/td][td][/td][td]Erstelle eine quadratische Funktion, indem du [math]g\left(x\right)=x^2[/math] in das [i]Eingabefeld[/i] eingibst.[/td][/tr][tr][td]5.[/td][td][/td][td]Verwende den Befehl [math]Schnittpunkt\left(f,g\right)[/math], um die Schnittpunkte von [i]f(x)[/i] und [i]g(x)[/i] zu erstellen. Die Schnittpunkte [i]A[/i] und [i]B[/i] werden in der [i]Grafik-Ansicht [/i]angezeigt, während die Koordinaten der Punkte in der [i]Algebra-Ansicht[/i] angezeigt werden[i].[/i][br][/td][/tr][tr][td][/td][td][icon]/images/ggb/toolbar/mode_intersect.png[/icon][/td][td][b]Anmerkung:[/b] Du kannst auch das [i]Schnittpunkt [/i]Werkzeug aus der [i]Werkzeug-Ansicht [/i]verwenden und die Funktionen auswählen, um die Schnittpunkte zu erstellen. [/td][/tr][tr][td]6.[/td][td][/td][td]Bewege die Schieberegler für[i] a [/i]und [i]b[/i] und beobachte, wie sich die Schnittpunkte [i]A[/i] und [i]B [/i]deinen Änderungen anpassen.[br][/td][/tr][tr][td]7.[/td][td][img width=24,height=24]https://lh5.googleusercontent.com/EeYLvel9HmsnYD7ZRVm-HBQtblHhlB35cdQzXdG11nyuG3R7BCgnyC_l3L8aKn1R4wNkQnlMJHA72jcGN8n5f2RRahLZMiuy01yMfDJFEssc0gxkkfajbgHSyt1KTilGP0RyH5NA[/img][/td][td]Wähle den Graph von [i]f(x) [/i]und [i]g(x)[/i] aus und ändere die Farbe der Funktionsgraphen mit Hilfe der [i]Gestaltungsleiste[/i], um die Konstruktion zu verbessern.[br][/td][/tr][/table]
Versuche es selbst...
Darstellung von Komplexen Zahlen
Aufgabe
Stelle eine komplexe Zahl dar und ändere ihre Koordinaten in Polarkoordinaten. [br][br]Erforsche die Konstruktion und lerne, wie du komplexe Zahlen im [url=https://www.geogebra.org/graphing]GeoGebra Grafikrechner[/url] darstellen kannst. Danach versuche es selbst, indem du die folgenden Anleitungen befolgst.
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/1/18/Algebra_new.svg/32px-Algebra_new.svg.png[/img][/td][td]Öffne die [i]Eingabehilfe[/i] in der [i]Algebra-Ansicht [/i]und wähle [i]Text.[/i][/td][/tr][tr][td]2.[/td][td][/td][td]Kopiere den folgenden Text in das [i]Eingabefeld [/i]und drücke die [i]Eingabetaste:[/i][br][/td][/tr][tr][td][/td][td][/td][td]CCSS.MATH.CONTENT.HSN.CNB.4[br]Represent complex numbers on the complex plane in rectangular and polar form (including real and imaginary numbers), and explain why the rectangular and polar form of a given complex number represent the same number.[/td][/tr][tr][td]3.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_complexnumber.png[/icon][/td][td]Öffne die [i]Werkzeug-Ansicht[/i] und suche nach dem [i]Komplexe Zahl [/i]Werkzeug. Wähle dieses Werkzeug aus und klicke an einer beliebigen Stelle in der [i]Grafik-Ansicht, [/i]um eine komplexe Zahl zu erstellen. [br][b]Anmerkung: [/b]Die komplexe Zahl wird automatisch mit [i]z[sub]1[/sub][/i] bezeichnet und ihre Koordinaten werden in der [i]Algebra-Ansicht[/i] angezeigt. [br][/td][/tr][tr][td]4.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/30/Menu-options.svg/32px-Menu-options.svg.png[/img][/td][td]Öffne die [i]Global[/i]-[i]Einstellungen[/i] und ändere die Schriftgröße. [/td][/tr][tr][td]5.[/td][td][img width=16,height=16]https://wiki.geogebra.org/uploads/thumb/2/25/Stylingbar_caption.svg/16px-Stylingbar_caption.svg.png[/img][img width=16,height=16]https://wiki.geogebra.org/uploads/thumb/b/bd/Stylingbar_point.svg/16px-Stylingbar_point.svg.png[/img][/td][td]Wähle die komplexe Zahl in der [i]Grafik-Ansicht [/i]aus und ändere ihre Einstellungen. Wähle im Beschriftungsmenü [i]Wert anzeigen. [/i]Ändere auch die Größe des Punktes. [br][b]Anmerkung: [/b]In der Mobile-App kannst du das Kontextmenü öffnen, indem du den [i]Mehr-[/i]Button auswählst. Klick auf [i]Beschriftungsstil[/i] und wähle [i]Wert. [/i][br][/td][/tr][tr][td]6.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/34/Algebra_hidden.svg/32px-Algebra_hidden.svg.png[/img][/td][td]Gib [math]z_2=z_1[/math] in das [i]Eingabefeld[/i] ein, drücke die [i]Eingabetaste[/i][i] [/i]und blende die neue komplexe Zahl aus, indem du links auf den [i]aktiven[/i] [i]Sichtbarkeits[/i]-Button klickst. [/td][/tr][tr][td]7.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/4/41/Icon-menu.svg/16px-Icon-menu.svg.png[/img][/td][td]Öffne in der [i]Algebra-Ansicht [/i]das Kontextmenü, indem du auf den [i]Mehr[/i]-Button von [i]z[sub]2[/sub][/i] klickst und wähle den Tab [i]Algebra[/i] aus. Ändere die Koordinaten in Polarkoordinaten und schließe die Einstellungen. Die komplexe Zahl [i]z[sub]2[/sub][/i] wird nun in der [i]Algebra-Ansicht[/i] in Polarkoordinaten angezeigt. [br][b]Anmerkung: [/b]In der Mobile-App gib [math]z_2=InPolar(z_1)[/math] ein, um die Polarkoordinaten in der [i]Algebra-Ansicht [/i]anzuzeigen. [/td][/tr][tr][td]8.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Bewege den Punkt [i]z[sub]1[/sub][/i] in der [i]Grafik-Ansicht[/i] und beobachte, wie sich die Werte in der [i]Algebra-Ansicht [/i]ändern. [/td][/tr][tr][td]9.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/30/Menu-options.svg/32px-Menu-options.svg.png[/img][/td][td]Öffne die Einstellungen und wähle [i]Koordinatengitter anzeigen[/i]. Aktiviere das [i]Polarkoordinatensystem. [/i][br][b]Anmerkung:[i] [/i][/b]In der Mobile-App wähle [i]Koordinatengitter anzeigen [/i]und ändere die [i]Art des Koordinatengitters [/i]auf [i]Polarkoordinatensystem.[/i][br][/td][/tr][/table]
