Paseos Matemáticos: sondeando la profundidad del estanque

Álvaro Martínez Sevilla, Nov 7, 2017

Una mirada a los Paseos Matemáticos con GeoGebra y sus posibilildades para la investigación en historia del arte y matemáticas

Table of Contents

  1. El proyecto Paseos Matemáticos por Granada
    1. Descripción
    2. Objetivos
    3. Direcciones de futuro
  2. Divulgación de las Matemáticas
    1. Aritmética visual
    2. El uso de polígonos estrellados para representar los rayos solares
    3. Cálculo vectorial aplicado a la escultura
    4. Modelo matemático de las flores en un jarrón
    5. Modelo 3D de mocárabes
  3. Desde las matemáticas a la interpretación artística
    1. Análisis de la funcionalidad de arcos y dinteles
    2. Buscando el centro de arcos ojivales y carpaneles
    3. Una simulación para comprender las luces y sombras del barroco
    4. Los primeros alfabetos algorítmicos
  4. Investigación en Historia del Arte
    1. La construcción mediante patronaje reticulado
    2. "El gran número" en el palacio imperial
    3. La ventana que codifica a Pi
  5. Descubriendo matemáticas a partir del arte
    1. Nuevo Lugar Geométrico a partir de un problema urbanístico
    2. Nuevo problema de geometría computacional

1.

El proyecto Paseos Matemáticos por Granada

[i][/i]

  • 1. Descripción
  • 2. Objetivos
  • 3. Direcciones de futuro

1.1.

Descripción

El Proyecto Paseos Matemáticos por Granada
[size=100][br][list][*][b]Actividades de Divulgación:[/b] LNI, PiDay, Semanas de la Ciencia, Congresos de Divulgación, ...[br][/*][*][b]Turismo Matemático: [/b]proyecto conjunto con una empresa de Turismo Científico.[br][/*][*]Un [b]libro impreso basado en GeoGebra + volumen digital[/b]. Mas de 400 applets, junto con un disco con más monumentos, conceptos matemáticos y los ficheros GGB.[/*][*][b]Investigación conjunta [/b]en matemáticas e historia del arte.[/*][*][b]Equipo de trabajo:[/b] 3 matemáticos, 1 historiador del arte, con la ayuda de comunicadores científicos de la Fundación Descubre.[/*][/list][/size]
Grupos de divulgación en Paseos Matemáticos por Granada
– Álvaro Martínez Sevilla

1.2.

–

1.3.

–

2.

Divulgación de las Matemáticas

  • 1. Aritmética visual
  • 2. El uso de polígonos estrellados para representar los rayos solares
  • 3. Cálculo vectorial aplicado a la escultura
  • 4. Modelo matemático de las flores en un jarrón
  • 5. Modelo 3D de mocárabes

2.1.

Aritmética visual

Algunas cartelas nos permiten hacer aritmética visual[br][br]Como [math]2\cdot\Phi=\sqrt{5}+1[/math] entonces [math]\Phi=\frac{\left(\sqrt{5}+1\right)}{2}[/math]
– Álvaro Martínez Sevilla

2.2.

–

2.3.

–

2.4.

–

2.5.

–

3.

Desde las matemáticas a la interpretación artística

  • 1. Análisis de la funcionalidad de arcos y dinteles
  • 2. Buscando el centro de arcos ojivales y carpaneles
  • 3. Una simulación para comprender las luces y sombras del barroco
  • 4. Los primeros alfabetos algorítmicos

3.1.

Análisis de la funcionalidad de arcos y dinteles

Podemos analizar también la sustentación de dinteles y arcos, y si la disposición de las dovelas es óptima o no.
Catedral. Puerta del Ecce Homo.
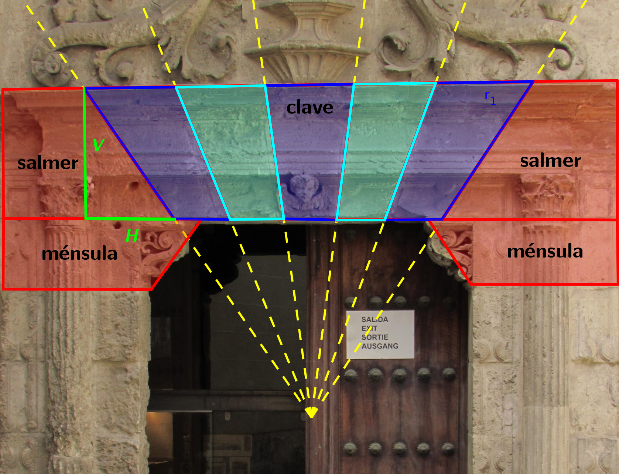
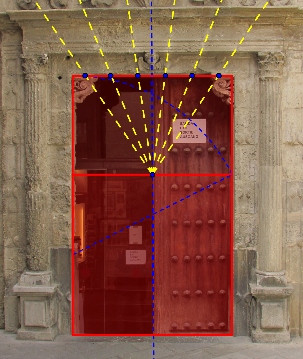
La piedra de sustentación o [b][i]enjarje[/i][/b] es casi óptima. Las superficies de ésta reciben de manera casi perpendicular las fuerzas transmitidas por el arco.
Lonja del Comercio (de la seda). Granada
– Álvaro Martínez Sevilla

3.2.

–

3.3.

–

3.4.

–

4.

Investigación en Historia del Arte

  • 1. La construcción mediante patronaje reticulado
  • 2. "El gran número" en el palacio imperial
  • 3. La ventana que codifica a Pi

4.1.

La construcción mediante patronaje reticulado

Casa de los Tiros. Granada
Se trata de un enigmático palacio renacentista, uno de los que más misterio encierra, con 3 polígonos de bronce sobre la puerta principal ([b]un triángulo, un cuadrado y un octógono[/b]) nunca explicados por los historiadores del arte.[br][br]Pero encontramos que estos forman parte de un [b]retículo triangular[/b] que define los principales elementos de la fachada, de la misma manera que [b]"el gran número"[/b] define algunos edificios renacentistas en Italia, pero con una geometría completamente singular con muchas y muy ricas interpretaciones artísticas.
– Álvaro Martínez Sevilla

4.2.

–

4.3.

–

5.

Descubriendo matemáticas a partir del arte

  • 1. Nuevo Lugar Geométrico a partir de un problema urbanístico
  • 2. Nuevo problema de geometría computacional

5.1.

Nuevo Lugar Geométrico a partir de un problema urbanístico

[size=100]En la principal puerta ceremonial de la Catedral de Granada, [b]La Puerta del Perdón[/b], en una calle estrecha de la ciudad, nos podemos preguntar:[br][/size][br][b]¿Cuál es la distancia correcta para observar de un vistazo, (sin desplazamiento de la vista) esta puerta?[br][/b][br]El conjunto de puntos desde los que podemos ver la puerta completa (dos primeras plantas) con el ángulo visual humano (aprox 30 º), forma un lugar geométrco que se conoce como [b]Curva [/b][b]Isóptica de un segmento [/b]o más específicamente.[b] Arco Capaz[/b]. Está históricamente asociado al Problema de Pothenot, y puede ser construido en GeoGebra tomando en consideración ambos lados.
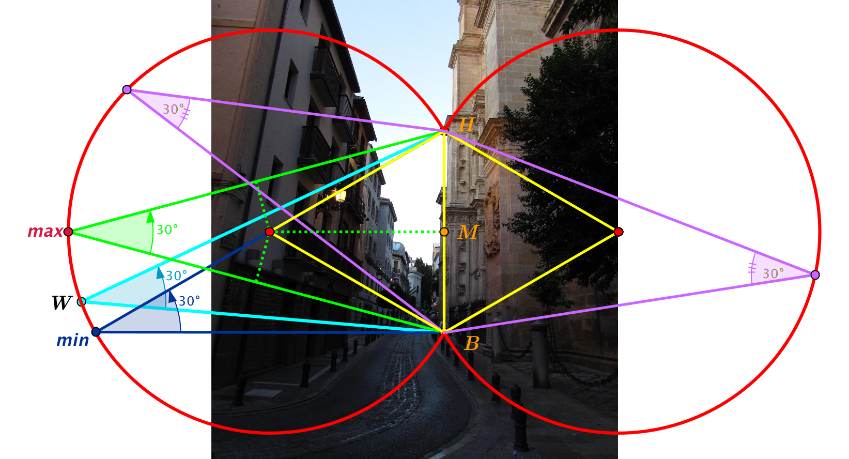
Pero en vez de tomar el [b]lugar geométrico[/b] normal en GeoGebra para este problema, podemos generalizar este concepto preguntándonos:[br][br][b]¿Cuál es el lugar geométrico para un problema análogo si contamos con un ángulo de visión humana comprendido entre 30º y 35º [/b][b]? [/b](como ocurre de hecho)[br][br]El resultado es un L.G. no descrito hasta el momento (hasta donde conocemos), que hemos llamado [b]Lunula Capaz[/b]. Y podemos visualizarlo en GeoGebra activando la traza en la siguiente construcción.
– Álvaro Martínez Sevilla

5.2.

–

Information