Dominio, rango y desplazamiento vertical de una función
1.3 Dominio y rango de una función
Tútilizando la ecuación y la gráfica de la función [math]f\left(x\right)=3x^2[/math] responde lo siguiente:[br][list=1][*]¿Para qué valores de [math]x[/math] está definida [math]f\left(x\right)[/math]?[/*][*]¿Cuáles son los posibles valores para [math]f\left(x\right)[/math]?[/*][/list]
Solución: Dar clic en cada botón habilitado, luego dale play a la construcción y observarás como los puntos en x se distribuyen en y=f(x).
Definición:
Dominio de una función ([math]D_{_f}[/math]), es el conjunto de todos los números [math]x[/math] para los cuales [math]f\left(x\right)[/math] está definida.[br]Rango de una función ([math]R_f[/math]), es el conjunto de todos los posibles valores para [math]f\left(x\right)[/math].[br][br]En el caso de las funciones lineales, tanto el dominio como el rango son el conjunto de los números reales, es decir [math]\mathbb{R}[/math]. Mientras que para funciones de la forma [math]f\left(x\right)=ax^2[/math] el dominio es [math]\mathbb{R}[/math] y el rango depende del valor de [math]a[/math]:[br][list=1][*]Si [math]a[/math]>0, entonces [math]R_f=[/math][0, ∞[[/*][*]Si [math]a[/math]<0, entonces [math]R_f=[/math]]-∞, 0][/*][/list]
Para las funciones lineales, observamos que el dominio y rango son los reales. (Darle play para visualizar la construcción)
Para las funciones cuadráticas, el dominio son todos los reales; pero para el rango depende del valor de a. (Darle play para observar como cambia las gráficas)
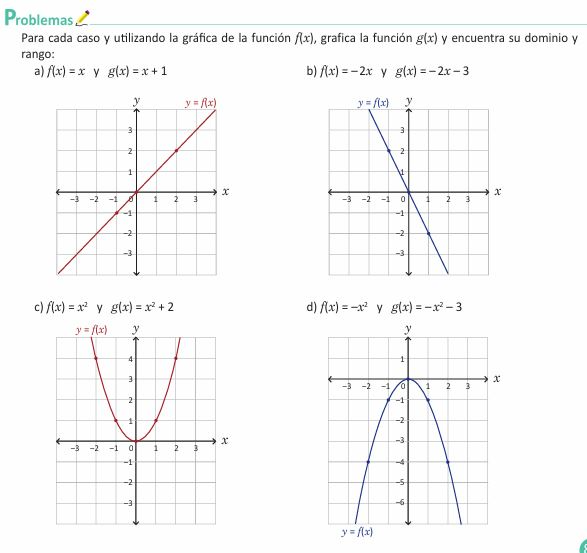
Resuelve todos los ejercicios que se les proponen.

2.1 Desplazamiento vertical.
Utilizando la gráfica de la función [math]f\left(x\right)=2x^2[/math] realiza lo siguiente:[br][list=1][*]Grafica las funciones [math]g\left(x\right)=2x^2+3[/math] y [math]h\left(x\right)=2x^2-2[/math]. ¿Cuál es el dominio y el rango en cada una?[/*][*]Explica qué le ocurre a la gráfica de [math]f[/math] para obtener las gráficas de [math]g[/math] y [math]h[/math].[/*][/list]
Solución: Dar clic para observar la construcción realizada en Geogebra.
Definición:
Dada una función [math]f\left(x\right)[/math] y un número real [math]k[/math] diferente de cero, la gráfica de la función [math]g\left(x\right)=f\left(x\right)+k[/math] es un desplazamiento vertical de k unidades de la gráfica de [math]f[/math], y: Si k>0 entonces la gráfica se desplaza hacia arriba, y si k<0 entonces la gráfica se desplaza hacia abajo.[br][br]Si [math]f\left(x\right)=ax^2[/math] entonces la gráfica de [math]g\left(x\right)=ax^2+k[/math] es una parábola con vértice en (0,k), y:.[br][list=1][*]Si a >0 entonces [math]R_f=[/math][k, ∞[[/*][*]Si a<0 entonces [math]R_f=[/math]]-∞. k][/*][/list]
Resolver todos los ejercicios en tu cuaderno.