Trigonometric Functions

Tim Brzezinski, Dec 28, 2016

Table of Contents

  1. Working with Radians
    1. What is a Radian?
    2. Constructing Angles Given Radian Measure
    3. 1 Radian: Clear Definition
    4. Animation 69
    5. Radian Illustrator
    6. Movie: Radians to Revs
    7. Quiz: Sketching Angles in Standard Position
    8. DEG to RAD and RAD to DEG Illustrator
    9. DEG to RAD and RAD to DEG: Question Generator
  2. Angles in Standard Position, Coterminal Angles, Trig Ratios
    1. Angles in Standard Position
    2. Animation 176
    3. Angle Orientations (Standard Position)
    4. Animation 180
    5. Animation 181
    6. Coterminal Angles Action!!!
    7. Animation 183
    8. Quiz: Sketching Angles in Standard Position
    9. Coterminal Angles: Question Generator
    10. Defining Trigonometric Ratios
    11. Unit Circle and Sine Graph
    12. Unit Circle and Tangent Graph
    13. Unit Circle and Cosine Graph
  3. Trig Functions of Special Angles
    1. Right Triangle Generator for Right Triangle Trigonometry
    2. Quiz: Evaluating Trigonometric Functions of Angles Given a Point on its Terminal Ray
    3. Evaluating Trig Functions Given a Point on the Terminal Ray
    4. Quiz: Quadrant Logic (Trig)
    5. Trig Quadrant Logic (2)
    6. Quiz: Evaluating Trig FNS of Angles (Quadrant Logic): V1
    7. Quiz: Evaluating Trig FNS of Angles WITH Quadrant Logic (V2)
    8. Right Triangle Trigonometry: Intro
    9. True Meaning of Sine, Cosine, Tangent Ratios within Right Triangles
    10. Right Triangle Solver: Formative Assessment
    11. Right Triangle Trig: Solving for Sides (2)
    12. Quiz: Expressing Angles Using Inverse Trigonometric Function
    13. Trig Ratio Estimations (Right Triangle Context)
    14. Trig Ratio Estimations (Quiz: V1)
    15. Trig Ratio Estimations (Quiz: V2)
    16. Isosceles Right Triangle: Quick Investigation
    17. Special Right Triangle (I)
    18. Another Special Right Triangle (Guided Discovery)
    19. Special Right Triangle (II)
    20. 30-60-90 Triangle
    21. Special Right Triangles: Basic Questions
    22. Quiz: Special Right Triangles
    23. Trig Function Values (30 Degrees)
    24. Animation 148
    25. Trig Function Values (45 Degrees)
    26. Animation 146
    27. Trig Function Values (60 Degrees)
    28. Animation 147
    29. Rads and Revs: Quick Conceptual Insight
    30. Trig Reference Circle: Choose Your Own Radius
    31. Trig Reference Circle (2): Choose Your Own Radius
    32. Trig Circle: Coordinates of Special Angle Values
    33. Special Angles in Standard Position: Intro (V1)
    34. Special Angles in Standard Position: Intro (V2)
    35. Special Angles in Standard Position: Intro (V2) - Part 2
    36. Animation 177
    37. Animation 178
    38. Special Angles in Standard Position: Intro (V3)
    39. Animation 182
    40. Quiz 1: Trigonometric Functions of Special Angles
    41. Quiz 2: Trigonometric Functions of Special Angles
  4. Even and Odd Functions
    1. Sine and Cosecant Functions (Special Property)
    2. Sine Identity
    3. Animation 150
    4. Cosine and Secant Functions (Special Property)
    5. Cosine Identity
    6. Animation 149
    7. Tangent and Cotangent Functions (Special Property)
    8. Animation 145
    9. Tangent Identity
    10. Animation 151
  5. Graphing and Writing Trig Functions
    1. Sine Spaghetti (by Steve Phelps)
    2. Cosine Spaghetti
    3. Sine and Cosine Graphing Template
    4. Sine and Cosine π-friendly Graphing Template
    5. Sine Function Anatomy and Exploration
    6. Unit Circle to Sine and Cosine Functions
    7. Sine & Cosine Period Action (1)!
    8. Animation 190
    9. Animation 191
    10. Sine & Cosine Period Action (2)!
    11. Tangent Function Exploration
    12. Tangent Period Action (1)!
    13. Tangent Period Action (2)!
    14. Animation 192
    15. Cotangent Function Exploration
    16. Transforming Sine and Cosine Functions (1): Dynamic Illustrator
    17. Transforming Sine and Cosine Functions (2): Dynamic Illustrator
    18. Transforming the Sine Function (All Transformations)
    19. Graphing Sine & Cosine Functions (II)
    20. Graphing Sine & Cosine Functions (I)
    21. Transformations of a Sinusoid
    22. Basic Trig Graphing Open Middle Problem
    23. Quiz: Graphing Sine & Cosine Functions (Amplitude & Vertical Shift Only)
    24. Writing Sine and Cosine Functions (with Amplitude & Vertical Shift Changes)
    25. Open Middle: Graphing Trig Functions Exercise
    26. Open Middle: Graphing Trig Functions Exercise (2)
    27. Modeling with Trigonometric Functions
    28. Ferris Wheel Action!!!
  6. Inverse Trig Functions
    1. Using Inverse Trig Functions to Express Angle Measures
    2. Creating Inverse Sine and Inverse Cosine Functions
    3. Evaluating Inverse Trig Functions of Special Ratios
    4. Compositions of Trig & Inverse Trig Functions (1)
    5. Evaluating Compositions of Trig & Inverse Trig Functions (2)
    6. Inverse Relations: Graphs
    7. Sine Function Domain Restriction Options?
    8. Cosine Function Domain Restriction Options?
    9. Tangent Function Domain Restriction Options?
    10. Inverse Trig Functions: Intuitive Explorations
  7. Solving Trig Equations and Modeling
    1. Open Middle: Trigonometric Equation (1)
    2. Open Middle: Trigonometric Equation (2)
    3. Open Middle: Creating Trig EQ's Exercise Set
    4. Ferris Wheel (1): Modeling with Trigonometric Functions
    5. Ferris Wheel (2): Modeling with Trigonometric Functions
    6. Interesting Triangles Phenomenon
  8. Proving Trig Identities
    1. New Trig IDs From Similar Right Triangles
    2. New Trig ID's from Similar Right Triangles (V2)
    3. Pythagorean Trigonometric Identity (1)
    4. Trig Identity via Areas: Dynamic Illustrator
    5. Trig Identity via Areas (2): Dynamic Illustrator
    6. Trig ID Movie (II)
    7. Trig ID Movie (III)
  9. Proving Advanced Trig Identities
    1. Law of Sines: Intro via Areas
    2. Open Middle: Ambiguous Case Setups
    3. Exploring Sines: Another Key Triangle Relationship
    4. Sine & Cosine of a Sum: Discovery
    5. Trig ID: Geometric Investigation
    6. Trig Identity (4) - Geometric Investigation
    7. Tangent of a Sum: Discovery
    8. Tangent of a Difference: Trig Identity Puzzle + Proof!
    9. Cotangent of a Sum: Discovery
    10. Bizzare Trig Identity?
    11. Animation 105
    12. sin(75) & cos(75) activity
    13. Trig Identity Shown Graphically
    14. Double Angle Trig Identity: Proof via Equal Areas
  10. Other Functions Resources
    1. Functions Resources

1.

Working with Radians

  • 1. What is a Radian?
  • 2. Constructing Angles Given Radian Measure
  • 3. 1 Radian: Clear Definition
  • 4. Animation 69
  • 5. Radian Illustrator
  • 6. Movie: Radians to Revs
  • 7. Quiz: Sketching Angles in Standard Position
  • 8. DEG to RAD and RAD to DEG Illustrator
  • 9. DEG to RAD and RAD to DEG: Question Generator

1.1.

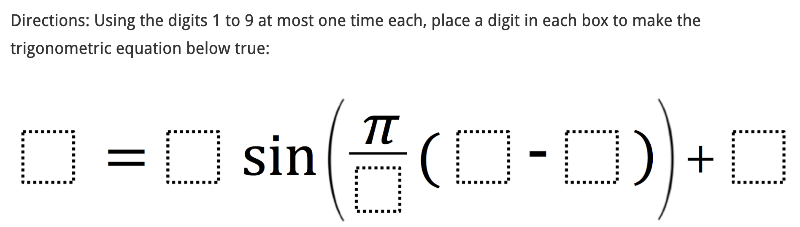
What is a Radian?

Interact with this app for a few minutes. Then answer the questions that follow.
A [b]radian[/b] is another unit of angle measure (like degrees). Solely from what you've seen above (and without using Google), [b]describe, in your own words, what it means for an angle to measure one radian. [/b]
We know a circle is a full arc that measures 360 degrees. From what you've seen, approximate the number of radians that make a full circle (revolution).
– Tim Brzezinski

1.2.

–

1.3.

–

1.4.

–

1.5.

–

1.6.

–

1.7.

–

1.8.

–

1.9.

–

2.

Angles in Standard Position, Coterminal Angles, Trig Ratios

  • 1. Angles in Standard Position
  • 2. Animation 176
  • 3. Angle Orientations (Standard Position)
  • 4. Animation 180
  • 5. Animation 181
  • 6. Coterminal Angles Action!!!
  • 7. Animation 183
  • 8. Quiz: Sketching Angles in Standard Position
  • 9. Coterminal Angles: Question Generator
  • 10. Defining Trigonometric Ratios
  • 11. Unit Circle and Sine Graph
  • 12. Unit Circle and Tangent Graph
  • 13. Unit Circle and Cosine Graph

2.1.

Angles in Standard Position

The angle drawn below in the coordinate plane is classified as being drawn in [b]STANDARD POSITION. [br][br][/b]Interact with the applet for a minute.[br]Then answer the question that follows.
ANGLE IN STANDARD POSITION:
1.
What does it mean for an angle drawn in the coordinate plane to be drawn in [b]STANDARD POSITION? [br][br][/b](Your definition should list 2 criteria.)
– Tim Brzezinski

2.2.

–

2.3.

–

2.4.

–

2.5.

–

2.6.

–

2.7.

–

2.8.

–

2.9.

–

2.10.

–

2.11.

–

2.12.

–

2.13.

–

3.

Trig Functions of Special Angles

  • 1. Right Triangle Generator for Right Triangle Trigonometry
  • 2. Quiz: Evaluating Trigonometric Functions of Angles Given a Point on its Terminal Ray
  • 3. Evaluating Trig Functions Given a Point on the Terminal Ray
  • 4. Quiz: Quadrant Logic (Trig)
  • 5. Trig Quadrant Logic (2)
  • 6. Quiz: Evaluating Trig FNS of Angles (Quadrant Logic): V1
  • 7. Quiz: Evaluating Trig FNS of Angles WITH Quadrant Logic (V2)
  • 8. Right Triangle Trigonometry: Intro
  • 9. True Meaning of Sine, Cosine, Tangent Ratios within Right Triangles
  • 10. Right Triangle Solver: Formative Assessment
  • 11. Right Triangle Trig: Solving for Sides (2)
  • 12. Quiz: Expressing Angles Using Inverse Trigonometric Function
  • 13. Trig Ratio Estimations (Right Triangle Context)
  • 14. Trig Ratio Estimations (Quiz: V1)
  • 15. Trig Ratio Estimations (Quiz: V2)
  • 16. Isosceles Right Triangle: Quick Investigation
  • 17. Special Right Triangle (I)
  • 18. Another Special Right Triangle (Guided Discovery)
  • 19. Special Right Triangle (II)
  • 20. 30-60-90 Triangle
  • 21. Special Right Triangles: Basic Questions
  • 22. Quiz: Special Right Triangles
  • 23. Trig Function Values (30 Degrees)
  • 24. Animation 148
  • 25. Trig Function Values (45 Degrees)
  • 26. Animation 146
  • 27. Trig Function Values (60 Degrees)
  • 28. Animation 147
  • 29. Rads and Revs: Quick Conceptual Insight
  • 30. Trig Reference Circle: Choose Your Own Radius
  • 31. Trig Reference Circle (2): Choose Your Own Radius
  • 32. Trig Circle: Coordinates of Special Angle Values
  • 33. Special Angles in Standard Position: Intro (V1)
  • 34. Special Angles in Standard Position: Intro (V2)
  • 35. Special Angles in Standard Position: Intro (V2) - Part 2
  • 36. Animation 177
  • 37. Animation 178
  • 38. Special Angles in Standard Position: Intro (V3)
  • 39. Animation 182
  • 40. Quiz 1: Trigonometric Functions of Special Angles
  • 41. Quiz 2: Trigonometric Functions of Special Angles

3.1.

Right Triangle Generator for Right Triangle Trigonometry

Math Teachers and Students:
Here, we have a custom tool (far right) that lets you quickly construct a right triangle by simply plotting 2 points and THEN entering the measure of one of its acute interior angles. [br][br][b]Note: [/b][br]If you select the RightTriangle tool (far right), simply plot 2 points. Then, enter in the measure of any acute angle. (You can also, if you choose, enter [math]\alpha[/math] = name of slider) if you wish to quickly change the size of this acute angle.
Quick (Silent) Demo: How to Use
– Tim Brzezinski

3.2.

–

3.3.

–

3.4.

–

3.5.

–

3.6.

–

3.7.

–

3.8.

–

3.9.

–

3.10.

–

3.11.

–

3.12.

–

3.13.

–

3.14.

–

3.15.

–

3.16.

–

3.17.

–

3.18.

–

3.19.

–

3.20.

–

3.21.

–

3.22.

–

3.23.

–

3.24.

–

3.25.

–

3.26.

–

3.27.

–

3.28.

–

3.29.

–

3.30.

–

3.31.

–

3.32.

–

3.33.

–

3.34.

–

3.35.

–

3.36.

–

3.37.

–

3.38.

–

3.39.

–

3.40.

–

3.41.

–

4.

Even and Odd Functions

  • 1. Sine and Cosecant Functions (Special Property)
  • 2. Sine Identity
  • 3. Animation 150
  • 4. Cosine and Secant Functions (Special Property)
  • 5. Cosine Identity
  • 6. Animation 149
  • 7. Tangent and Cotangent Functions (Special Property)
  • 8. Animation 145
  • 9. Tangent Identity
  • 10. Animation 151

4.1.

Sine and Cosecant Functions (Special Property)

Suppose [math]\theta[/math] is an angle drawn in standard position. [color=#666666][b]Let [i]P[/i]([i]x[/i], [i]y[/i]) be any point in the coordinate plane[/b][/color] and let[color=#666666][b] [i]r[/i] = the distance from [i]P[/i] to the origin[/b][/color]. [br][br]Recall [math]sin\left(\theta\right)=\frac{y}{r}[/math] and [math]csc\left(\theta\right)=\frac{r}{y}[/math]. [br][br]Interact with the applet below for a minute or two. Then answer the questions that follow. [br][color=#666666][b](Be sure to move point [i]P[/i] to various locations!) [/b][/color][br][br]
1.
Regardless of where [i][color=#666666][b]P[/b][/color][/i] lies, what is the relationship between the values of the ratios [math]sin\left(-\theta\right)[/math] and [math]sin\left(\theta\right)[/math]?
2.
Regardless of where [i][color=#666666][b]P[/b][/color][/i] lies, what is the relationship between the values of the ratios [math]csc\left(-\theta\right)[/math] and [math]csc\left(\theta\right)[/math]?
3.
What do these 2 observations imply about the sine and cosecant functions? (Click [url=https://www.geogebra.org/m/pb8Drtd5]here[/url] and/or [url=https://www.geogebra.org/m/GY9tNvfB]here[/url] for a hint!)
– Tim Brzezinski

4.2.

–

4.3.

–

4.4.

–

4.5.

–

4.6.

–

4.7.

–

4.8.

–

4.9.

–

4.10.

–

5.

Graphing and Writing Trig Functions

  • 1. Sine Spaghetti (by Steve Phelps)
  • 2. Cosine Spaghetti
  • 3. Sine and Cosine Graphing Template
  • 4. Sine and Cosine π-friendly Graphing Template
  • 5. Sine Function Anatomy and Exploration
  • 6. Unit Circle to Sine and Cosine Functions
  • 7. Sine & Cosine Period Action (1)!
  • 8. Animation 190
  • 9. Animation 191
  • 10. Sine & Cosine Period Action (2)!
  • 11. Tangent Function Exploration
  • 12. Tangent Period Action (1)!
  • 13. Tangent Period Action (2)!
  • 14. Animation 192
  • 15. Cotangent Function Exploration
  • 16. Transforming Sine and Cosine Functions (1): Dynamic Illustrator
  • 17. Transforming Sine and Cosine Functions (2): Dynamic Illustrator
  • 18. Transforming the Sine Function (All Transformations)
  • 19. Graphing Sine & Cosine Functions (II)
  • 20. Graphing Sine & Cosine Functions (I)
  • 21. Transformations of a Sinusoid
  • 22. Basic Trig Graphing Open Middle Problem
  • 23. Quiz: Graphing Sine & Cosine Functions (Amplitude & Vertical Shift Only)
  • 24. Writing Sine and Cosine Functions (with Amplitude & Vertical Shift Changes)
  • 25. Open Middle: Graphing Trig Functions Exercise
  • 26. Open Middle: Graphing Trig Functions Exercise (2)
  • 27. Modeling with Trigonometric Functions
  • 28. Ferris Wheel Action!!!

5.1.

Sine Spaghetti (by Steve Phelps)

Original creativity and design in the app below by [url=https://www.geogebra.org/u/stevephelps]Steve Phelps[/url].
Move the [b]LARGE POINT [i]P[/i] [/b]to various locations around the circle. Each time you do, [br][list=1][*]Press the [b][color=#cc0000]Make Segment[/color][/b] button. [/*][*]Drag the segment you just made so its endpoint that originally touched the horizontal axis now touches the open-holed point on the right. (See quick screencast below.) [/*][*]Repeat steps (1) - (2) numerous times. Get as many segments dragged to the right as you can. [/*][*]Use the [b]PEN tool[/b] to draw a curve that connects the other endpoints of the segments that do not touch the horizontal axis. [/*][/list]
What does this curve look like to you? Describe.
– Tim Brzezinski, Steve Phelps

5.2.

–

5.3.

–

5.4.

–

5.5.

–

5.6.

–

5.7.

–

5.8.

–

5.9.

–

5.10.

–

5.11.

–

5.12.

–

5.13.

–

5.14.

–

5.15.

–

5.16.

–

5.17.

–

5.18.

–

5.19.

–

5.20.

–

5.21.

–

5.22.

–

5.23.

–

5.24.

–

5.25.

–

5.26.

–

5.27.

–

5.28.

–

6.

Inverse Trig Functions

  • 1. Using Inverse Trig Functions to Express Angle Measures
  • 2. Creating Inverse Sine and Inverse Cosine Functions
  • 3. Evaluating Inverse Trig Functions of Special Ratios
  • 4. Compositions of Trig & Inverse Trig Functions (1)
  • 5. Evaluating Compositions of Trig & Inverse Trig Functions (2)
  • 6. Inverse Relations: Graphs
  • 7. Sine Function Domain Restriction Options?
  • 8. Cosine Function Domain Restriction Options?
  • 9. Tangent Function Domain Restriction Options?
  • 10. Inverse Trig Functions: Intuitive Explorations

6.1.

Using Inverse Trig Functions to Express Angle Measures

Use inverse trigonometric functions to enter 3 different exact values for the measure of angle A. Do the same for angle B. Then, approximate angle A's measure to the nearest tenth (at bottom).
Quick silent demo
– Tim Brzezinski

6.2.

–

6.3.

–

6.4.

–

6.5.

–

6.6.

–

6.7.

–

6.8.

–

6.9.

–

6.10.

–

7.

Solving Trig Equations and Modeling

  • 1. Open Middle: Trigonometric Equation (1)
  • 2. Open Middle: Trigonometric Equation (2)
  • 3. Open Middle: Creating Trig EQ's Exercise Set
  • 4. Ferris Wheel (1): Modeling with Trigonometric Functions
  • 5. Ferris Wheel (2): Modeling with Trigonometric Functions
  • 6. Interesting Triangles Phenomenon

7.1.

Open Middle: Trigonometric Equation (1)

Creation of this resource was inspired by this original Open Middle exercise created by Kevin Rees:
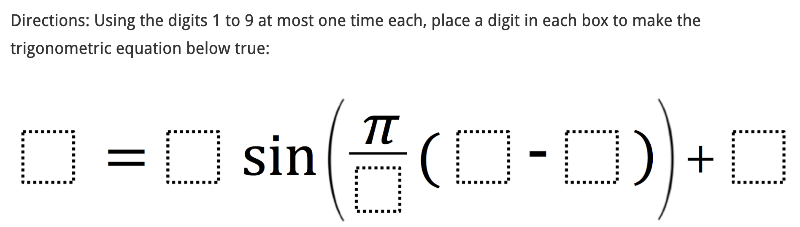
Directions: Using digits 1-9 AT MOST ONE TIME EACH, type a digit in each box to make the trigonometric equation below true. Build and modify as much as you need.
Directions: Using digits 1-9 AT MOST ONE TIME EACH, create another valid setup that is ENTIRELY DIFFERENT from the one you created above.
Directions: Using digits 1-9 AT MOST ONE TIME EACH, create another valid setup that is ENTIRELY DIFFERENT from the two setups you created above.
What is the LOWEST POSSIBLE OUTPUT (value that both sides equal) you can create given the constraints of this problem? Create a setup that shows this below.
What is the HIGHEST POSSIBLE OUTPUT (value that both sides equal) you can create given the constraints of this problem? Create a setup that shows this below.
– Tim Brzezinski

7.2.

–

7.3.

–

7.4.

–

7.5.

–

7.6.

–

8.

Proving Trig Identities

  • 1. New Trig IDs From Similar Right Triangles
  • 2. New Trig ID's from Similar Right Triangles (V2)
  • 3. Pythagorean Trigonometric Identity (1)
  • 4. Trig Identity via Areas: Dynamic Illustrator
  • 5. Trig Identity via Areas (2): Dynamic Illustrator
  • 6. Trig ID Movie (II)
  • 7. Trig ID Movie (III)

8.1.

New Trig IDs From Similar Right Triangles

Recall the definitions of the 6 trigonometric functions defined at an angle drawn in standard position within the coordinate plane. (These ratios were defined in terms of [i]x[/i], [i]y, [/i]& [i]r[/i]). [br][br]Interact with this diagram for a minute or two. (The 2 LARGE POINTS are moveable). [br]Then, answer the question prompts that follow.
1.
Explain why each segment IS what it is. (Some are much easier than others). [br][br]For example, how do we know the [b][color=#9900ff]purple segment has a length = to the tangent of[/color][/b] [math]\theta[/math]?
2.
How many pairs of similar triangles do you see here? How do we know these triangles you reference are all similar to each other?
3.
You have previously learned that similar triangles have corresponding sides that are in proportion. That is, ratios of corresponding sides of similar triangles are all equal in value. [br][br][i]Given this fact, try to author other trig identities from this picture.[/i] You can type them in the space below. Or, even better, feel free to type or use the digital pen to write them in the app below this space. [br]
Write some new trig identities here!
Write some new trig identities here! Use this space if you run out of room above.
– Steve Phelps, Tim Brzezinski

8.2.

–

8.3.

–

8.4.

–

8.5.

–

8.6.

–

8.7.

–

9.

Proving Advanced Trig Identities

  • 1. Law of Sines: Intro via Areas
  • 2. Open Middle: Ambiguous Case Setups
  • 3. Exploring Sines: Another Key Triangle Relationship
  • 4. Sine & Cosine of a Sum: Discovery
  • 5. Trig ID: Geometric Investigation
  • 6. Trig Identity (4) - Geometric Investigation
  • 7. Tangent of a Sum: Discovery
  • 8. Tangent of a Difference: Trig Identity Puzzle + Proof!
  • 9. Cotangent of a Sum: Discovery
  • 10. Bizzare Trig Identity?
  • 11. Animation 105
  • 12. sin(75) & cos(75) activity
  • 13. Trig Identity Shown Graphically
  • 14. Double Angle Trig Identity: Proof via Equal Areas

9.1.

Law of Sines: Intro via Areas

In the app below, points A and B are MOVEABLE. You can change the sizes of the colored angles using the two colored sliders in the lower left corner. Slide the long slider slowly and carefully watch what happens!
[img width=329,height=170]https://lh6.googleusercontent.com/MP__fZu80x1doBPReABsDuZddxJj0leoUvgMv70UrxfEpTMWH9GP7HKvIVpedWo1Fyc3Ww1ZrdCLY_l4LOa_nxirCJsGmRChdt3jwP0dIWAhks2_yvuMJNsWCI-bWRyHQi1iLETo[/img][br][br][br][br]What is the area of this rectangle in terms of [i][b]a[/b][/i] and [i][b]sin B[/b][/i]?
[img width=236,height=220]https://lh5.googleusercontent.com/bGoknLi6GkA-yFtCKiWWaplR8IH6-_ixHn8_hZ6X8wFAnQb1m50pMbqd-fa6EEGAFPSYF3nJAM4DJQSNbGAQRO9HBqLUqf1ac0iWUhGBTpw9ZAkDUjXUlOVK35Uu7hCjGozYBNK6[/img][br][br][br][br][br][br][br]What is the area of this rectangle in terms of[b] [i]b[/i] [/b]and [b][i]sin[/i] [i]A[/i][/b]?
What can we conclude about the areas of these two rectangles? Why can we conclude this?
Given your responses to the questions above, write an equation that expresses the relationship among [b][i]a[/i], [i]b[/i], sin [i]A[/i], and sin [i]B[/i]. [/b]
Copy the equation you wrote above in the app below. Then rewrite an equivalent equation so that a and sin(A) appear on one side of the equation and so b and sin(B) appear on the other side.
Quick (silent) demo
– Tim Brzezinski

9.2.

–

9.3.

–

9.4.

–

9.5.

–

9.6.

–

9.7.

–

9.8.

–

9.9.

–

9.10.

–

9.11.

–

9.12.

–

9.13.

–

9.14.

–

10.

Other Functions Resources

  • 1. Functions Resources

10.1.

Functions Resources

[list][*][b][url=https://www.geogebra.org/m/k6Dvu9f3]Interpreting Functions[/url][/b][/*][*][b][url=https://www.geogebra.org/m/uTddJKRC]Building Functions[/url][/b][/*][*][b][url=https://www.geogebra.org/m/GMvvpwrm]Linear, Quadratic, and Exponential Functions[/url][/b][/*][*][b][url=https://www.geogebra.org/m/aWuJMDas]Trigonometric Functions[/url][/b][/*][/list]
Half-life function: Quick Exploration. (Large point & slider moveable.)
What does it mean for a function to be odd? (Points moveable.)
– GeoGebra Team, Tim Brzezinski

Information