IM Geo.2.5 Lesson: Points, Segments, and Zigzags
If A is a point on the plane and B is a point on the plane, then A is congruent to B.
Try to prove this claim by explaining why you can be certain the claim must be true, or try to disprove this claim by explaining why the claim cannot be true. If you can find a counterexample in which the “if” part (hypothesis) is true, but the “then” part (conclusion) is false, you have disproved the claim.
Prove the conjecture:
If [math]AB[/math] is a segment in the plane and [math]CD[/math] is a segment in the plane with the same length as [math]AB[/math], then [math]AB[/math] is congruent to [math]CD[/math].
Prove or disprove the following claim:
“If [math]EF[/math] is a piece of string in the plane, and [math]GH[/math] is a piece of string in the plane with the same length as[math]EF[/math], then [math]EF[/math] is congruent to [math]GH[/math].”
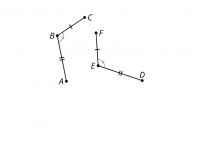
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAVwAAADdCAYAAAD3jcrlAAAgAElEQVR4Ae2dCdhW0/rGj+O4Ig2apGTMmCgqJ+GIkDITUpF5SjJLhkwZSqKSyBRCSMYMHTMZOmTIkJCxdMqUMdP6X791/iv7299+p+/b7373cD/Xta/9vnuv4Xnutda9137WsP9mJEJACAgBIRAJAn+LJBdlIgSEgBAQAkaEq0ogBISAEIgIARFuREArGyEgBISACFd1QAgIASEQEQIi3IiAVjZCQAgIARGu6oAQEAJCICIERLgRAa1shIAQEAIiXNUBISAEhEBECIhwIwJa2QgBISAERLiqA0JACAiBiBAQ4UYEtLIRAkJACIhwVQeEgBAQAhEhUBThXn311Wb8+PHLjquuusqcccYZ5pJLLgntOPbYY40/n2uvvdb8+eefEUHxVzZff/218R+zZ882n332WajHp59+at5+++1qeZF3MfLCCy+YMWPGmLFjxy47Tj75ZHPhhReaiy++uMbHsGHDzKGHHrosTZf+rbfeWoxaoYXxlwH/wevzzz8P5XjnnXfM/Pnzq+H/+++/h2aDEhICXgSKItz33nvPeI9XX33VPPfcc+Y///lPaMeUKVNsY/Lmw+9KEO7EiRPNBRdcUOWAgE455ZRQD8jxyCOPrJIP+d5zzz3eMsr5+4MPPjD+Y9q0aeaNN94wb775Zq0O0vGnzf8oJagcjjjiCHP66aeHcvTv39+cffbZVfA/77zzjAg3ylLOVl5FEW62IDGW5CF67/Hbb7/ZhkhjDOsgTQ5vPu531jAPstdh4T2D/R9//BHK4crRm777HaSPrgmB2iIgwq0tgoovBISAECgSgVAI1/UK3LnIvBUsxgi4XiRlKhECQiAcBGpFuDTK++67zzDg1bp1a7PJJpuYgQMH2mvcCxKuP/744+bf//534IF/mNfsXPGD0izXtbfeess8//zz9sBnzYHejoTuvPNOc8cdd9jj9ttvt/e45rXtiSeeMBzY7BXScHHdmXC1kU8++aRK3tOnT7f/sYHfH3/8cUH/5HfffWfOPfdcs88++5g99tjDnHDCCdYnjF+Y68722uhZStxnnnnGPPvss/ZwZRCEJZhjozuCsOSew9qdKTf3G985vutyCPUZ/PzCdfRydcb9xm6uvf7667FpD37dvf9ps0OHDrWXaDeurCg7fs+YMcM89dRT3ii2TF35OnurBEjhnxoRLo2O0WIGktq0aWNuvPFGO8DCIBeV6m9/+5u58sorAxsncXv16mW22247G65r167m8MMPt7MeKLDVV1/dHpVo3P7yRYeDDjrI7LzzzlZX7Ordu7clUMLSUHnIcP2f//ynncHAtf32289WPq5z7Lvvvuacc86pkjw48KByYXr27BnYIKtEKvDngQceMMccc8wybMH56KOPNmeddZY58MADbV6dO3e2DTkoKQi7ffv2tkwffvhhO+hGmay77rrWTgaxohQwAstDDjlkGU7oz8CWVwhHOeXDkjDEJUyHDh0sTpQJB+W811572XsMyIX9sCe9wYMH23JBD6/gR0YHpxvt4bDDDjOnnXaaGTJkiGnYsKHFnhk8/rjedCr5G/v23ntvM3LkSKsGdYY2jS2uTHhwQ8ReGTVq1LL7a6yxxjLC9oZJ2++SCZdCf+yxx0zTpk1tw1yyZEkVTACfCgTQU6dOrXLP+4enN2H8xEr6jB5z7/LLL/dGCfxNfvfee69N5+WXX87bgyNtSKhUgXzQZ8MNNzQLFy5cFp28eXAwDYuG4xXy2nLLLZfZ6L3nfmP7brvtZp/8hA9DSMc9zNDbK+iIHRw8HL3CvV122cXqjF1eOe6442wcr+3e+97fxOWhg20zZ86shos3LFPtFixY4L0U+Js082GJzeTXo0ePnFjyMMFu6ibpObw5U37cO/jgg0MnW9K//vrrza677poXC/RHB85eIT4Pee6RTj7Brtdee81cd911ZvLkyWbx4sX5ght69w6HvAHz3CRPL67eoExb5B4H4fzy7rvvmsaNG5vbbrut1nr4047r/5IJl7mjuA/o2QaBiKEOaMgkVxhXwYIq0f33328LiSdkvgpB2i4depprrrmm2X333a1LIwjwWbNm2XmrQffyXSOfzTbbzOpEZUa49uuvv9q5qrl0xDYqG3H9ODBti3tz5szJl3XJ98iHdBs0aGC++eabKvG516lTJ3uf3oVXHn30UXsd94NfeIOB8Pw2+MPxWskDjfz/9a9/mSZNmpgDDjjAEq8/LP+Zyw1BFCP5sLzrrrvsW1E+LOl9oZv/wcj8cvTdaaedzE8//VSMKiWFefrpp+2DIB921B/IHj0oB78wHZF7uHnyCS6R5s2bm9VWW81suummhl4jc+aD8ibPVq1aVcMjX/r+e6Tr3t6C2oD3Ae+f6kjcbt26majfmvw2RP2/JMKlQfHqtdJKK9nXzVzKLlq0yFaQVVZZJbBAKRzXC8Nn5RfXQ+Y1JKggXXj8W1RUzoSjgN1rSpAv7swzzyy6gbs83NkRO4ROPgMGDDBLly7Nq5+3wnmJBbLlgYXfKmzBd+kIxN/QmOS/8sor2/teYiUcWBMvaK4tfjjmq+YrC+zgtXeHHXaw7ibC8kACp7p161ZzY5AnDyLCFCO5sHzppZcsyfj9g9400aVdu3a25+29zvgDNrdt2zbQbm/YmvzmAc9bEed8Aha0hxVXXNEEvTE6lxZllEvAh140i1OwlzTnzZtnX+txUfzwww9Voj744IPWDUa4mgh5kAb4wQtBQhj3AO7Xr98y4kdXrsfZTRJkTxjXiiZcwHOkM2jQoLyNj4EXCoKD10q/uMZDBfv555+r3KbwnF+UAs0n9erVM3Pnzq0WhHjrrbee9SPT66FS4cKggeeqHNUS8V2AiJxN+KepMIUqK5gx8EQ8XlsR8uf/Nddc48shnL+ujDj7ZfTo0TZvv+7o6V5bObuBGq4jnJ988kl/clX+gwX+X1ZveYW47iHIq+MXX3xhcZs0aZLVhbpQjJCOH8v//ve/No2bbrqpYBI8xL2C+6lly5a2F86gTtjCmyDpex9sufKgDaywwgq2x+evUy+++KK1kU5OvvZAvXJ1zJsP+NJ733bbbQ29bf7zkIPgcSnUVPDHNmrUyK7Sy5cGC5qo7/Xr1zfwAvZR//Dx+m3Nl05a7hVNuBQoPjLAe+WVV/LaD8kRjoNelV+c/7Z79+7LRmBJH9/f+uuvb8mS367B++Pzn8Ji8CNXg+XpzgASBe10eeihh4KSKuoauvTt29emxSternz9ieFLI38GRbDx/PPPNyNGjChLZUNH9+aAreSHnsxOoKeJHrwCct0v7q2CMLgjaKSQNr7PYoTyIG6uMqOXvOeee9owhOOgp1+KeLGENBgoo5dUasNlifYWW2xhdSDNsAUC5e2uGLIlb2ZdgAdlQHlhD2fGMLjesWPHaiP8fp0pK8YygoS0eMDTXhz25FUqbi5tesvrrLOO7UG7a7nOrl6QLw9c3mgZo0GnLErRhPv9999bVwINulBB8aoMwLzGBYV1vTB8wfj61l57bRueEWlG2ospDBo2/rd8Qt5UDpYg86oWpEu++P57VBbsQl//q58/rPuPLe41vk+fPnZmRy5ScnFqeoZIXYOiR8PhHjg0MKbm5MobbLyk69LBJ+gffAvSj3TdKHXQfa6RB/sg8NZTLH7etPxY4h/OZY83nvc3aTC2gH34N0uN700r6Dc2MqDMwHIxaRPetYeNN97YzojhoYh+22+/vU2nmPZAGNLKJ4Shs8MDuBjdgtIiDeoUdakYIR96tNgD7tRJ3kyyKkUTLj4yQCumkh911FE2LPsE+AuW/zvuuKO9z+sSJEFFYZ4nrgR6HpB7MUJaNTmKSdsfht4YDYLXZnAIGuzzx+E/+jk86OX6B7KC4tT0Gr1IdGvRooV9aNE4wPfSSy+112nY+QRdaYz0RNAZlw3pXXTRRdXKMSidcpeFF0t6SYUIxq8j4amT2MRUOdJDOENEtRXSp9NAR8ClXShN4rgZGPTaXXtwb4G0t2LtJM9Sj0L6ee+jR5cuXYqu+y4urgswpz5RR7MsRROuewqfdNJJefHCT8PrFAAHjbhCAgyiNGvWrFpFcnl4B5jyZcYr/vLLL28HG3jqMsWEEVpGZ5k7yoAFAyKbb765HZ3feuutDTuQlSo8DPDH8SBgcxlsY/CsmIZAA3D+0dr4zIrRmd3b0A1S8Yrr+fJA8xMB/3ORDT4/0uOthnIrJMwd5Y2llCPIB58rHy+W/jmdueK468Rl/i72+P2HuE2C6qOLW8yZ9NmMqNR5vEzPQyce5N76xG/nHirGrfPhhx+WhLsro2JsIwz6QP6UMbaWIuxoh43M2y81bin5JCFs0YR7xRVXWNDwBXrFD6AbmMk1sMbrJOBT4P4Kxsg993IRgDdffhMfIijl8ObpTy/oP/NE8Su7kWbmjqIjh7sWFM9dQ7cNNtjAPgDKMe3I5UM58BBAL6bVeYUHBtdxhfjtx93CK3CQOKKm4fvLOVf4oLIgnaDrXCtFHJa4ovx25EsH3d20Mkb8/XF50LNApKZC+gzc+Qcji0mPAVjKxv/2ga08BLhX7EMpF8b0nIPuUS7FCPYxhY/FDcXUA3+auNKwoyadHX9aSf9fNOEyqgtoTAsDdAqQqUJccz03lrXyH4LifpC4gQB/BXNTyYjP8t44CA2TmRReXzG2ux6r34Ygnd2cZCqdv6EHhfdfI04x8QjDSHadOnWqTQFiniq4BvnfKQ/cOEENyfni/XMo/TpG9d9hWSqxOVfLWmutVa1efvXVV/YNKNdDHlwK4U/bYH5zrjqfCx/SZsoWZePP383A4F6xxJgrn9pcR0ceVrwdFcIhKB/iMycYO4KmHAbFSfO1ogkXsFmJxGs7rzjjxo0zEyZMsIXA/D9HtixRzVXxAJ80AN+/1h0nPNc5GFAhLAsf8hUy92pyFCpQ8sYGCJW9IfjvFbcwI9/iDxeeNLCpGHJ2cdzZYUDPtNAMCzf/Nqg3ymbk6OAIlwbMUl/S5xrTe/yNGvuZqcCy2lzl6fR053KUhUubc02wxGeO7dRbbMRmd9BRoL7mGtzlQUUvM5+/mLq66qqrFo2R1x7wAn/082PMDAeuu3uE5Te655Jy4I8eLC8m7ZoIM0LoCLi6V5M00hSnaMLFaAZUmFrCaxmNkVcVeh1uD4Sbb745sGAoLHqJfEnAVSJGxGlArgLRGNzaa2YDcG+rrbYKTM8VAKSBE5/eBT4wnsL4bfHf4sdlhJ2Ghn+Xnir+3kLLhcmXysFUHHTdf//9q8xBxQ/oRl25T4+fOAwAeoVwTP8if8KxQIN4uCSKFdfIiO/FyhsfosW35pZDgwFTz5hW54RXUtIAXxo2o8W4hkgfQiFtpvwxrYgGwlxadOXwE7FLM+iMm4h8SjmKmToFlm7gz2FRDJburYw41D1wcXtN8JBxeuZaYAMuhOGB5ydE7Gd65HLLLWff9AjrPVz99l+jvoM7+rv0yYO3Rf572wP5co/eL/forLj7fvyZJ+3sKfZMeeUT3jR5W2WFGzMnONCbtzUexAysHn/88dZ3zV4R6OgEfeAFt2iDesl9rmVZSiJcgKIB0rsFcAqMhs4mG0wdcpWBhuv1IzLDgUoDkXLmYEK0t4BIm7XVw4cPt6TOAMSXX36Zt2youDU58iVKhUA/dOZg4MjZRTynO4TmPbxhCEePlJVM3jD89ofLpwv3GIR0r8RBYZkM78UV/XioeN8gIAtWINFbpzGCO7hxHWLg9yOPPGJJmLnREPMNN9wQSDJBOrhrpFdqebi4+c7Yh3sDAnUHK8wKYYnvmjmu2Os9qL+UDVhx5FoSjC34Hd2DKkhHb7qFfoM1Ahm5vN357rvvtmXhzYOyZTYFHQDaQxDpe8OXin2h9FzHp5Bd3vtOH+Y3E997YKu3XrqwWTqXTLgOHArXNTAApweH3wmixVfmX0ro4hU604hIu1BjKpROmu6Dr2ustbHLYerO/rS47srUfy+r/8GDhxR1shJCmag9VAL58uRZY8J16lAh3MwE9yoDQeRq1C6ezsUh4Bp81nsGxaEVfiiWJcv/GD6uWU2x1oQLcG4QCcLF51mK3y+rwBdrt3tdq1QPq1g90xiOub74Ht9///00miebKoBAKIQLGbAogA071LMNtxRp9PRyJZVBoNQFFpXRUrkmBYFQCDcpxkpPISAEhEAlERDhVhJ95S0EhECmEBDhZqq4ZawQEAK5EHCD/kHnXHFKvS7CLRUxhRcCQiCVCLi59+7M/hiQL/vChCUi3LCQVDpCQAikCgGWfDMlMEwR4YaJptISAkIgFQiwgpY9JMLev1qEm4rqISOEgBAICwHnSihm+9VS8xThloqYwgsBIZBaBCBZ/LbFfJi0JiCIcGuCmuIIASGQOgRwH7BDG+6EcokIt1zIKl0hIAQShQADZAyUhe239YIgwvWiod9CQAhkEgGmfjFINm/evLLaL8ItK7xKXAgIgbgjMHXqVOu3Zf5tuUWEW26Elb4QEAKxRYAeLV8Z58stfGzAf4StuAg3bESVnhAQAolBgC+8BC3l5Rr+3LBFhBs2okpPCAgBIZADARFuDmB0WQgIASEQNgIi3LARVXpCQAgkFoEFCxaYGTNmlG3TfxFuYquGFBcCQiBMBE499dRl/txGjRqZSZMmhZm8TUuEGzqkSlAICIGkIcAn6f2DZ/Xr1zc///xzqKaIcEOFU4kJASGQRAROP/30aoQLAT/55JOhmiPCDRVOJSYEhEASERg9enQg4b733nuhmiPCDRVOJSYEhEASEViyZIlp3LhxFdI96KCDQjdFhBs6pEpQCAiBpCEwd+5cS7YdO3Y0ffv2NePHjy+LCSLcssCqRIWAEEgSAv369TN169Y1TAsrp4hwy4mu0hYCQiD2CEyfPt32bi+77LKy6yrCLTvEykAICIE4I7DNNtuYNm3aRKKiCDcSmJWJEBACcURgwoQJtnc7efLkSNQT4UYCszIRAkIgbggsXbrUtGrVyvTs2TMy1US4kUGtjISAEIgTAkOGDLG925dffjkytUS4kUGtjISAEIgLAnPmzLFkO2DAgEhVEuFGCrcyEwJCIA4I9OnTx9SrV88sXLgwUnVEuJHCrcyEgBCoNAKPPfaY7d2OGDEiclVEuJFDrgyFgBCoJAJdunQxbdu2rYgKItyKwK5MhYAQqAQCLNllF7C77767EtkbEW5FYFemQkAIRI0Ae9u2aNHC7L777lFnvSw/Ee4yKPRDCAiBNCMwePBg27udOXNmxcwU4VYMemUsBIRAVAi8++67lmwHDhwYVZaB+YhwA2HRRSEgBNKEQO/evU2DBg3MokWLKmqWCLei8CtzISAEyo3AI488Ynu3I0eOLHdWBdMX4RaESAGEgBBIMgKdO3c27dq1i4UJItxYFIOUEAJCoBwIjBs3zvZup0yZUo7kS05ThFsyZIogBIRAEhD48ccfTfPmzc2ee+4ZG3VFuLEpCikiBIRAmAi4T5+/+uqrYSZbq7REuLWCT5GFgBCIIwJvv/22dSUMGjQoVuqJcGNVHFJGCBRGYOjQoWbWrFnVAk6dOtWMGjWq2vUsXth///1No0aNzNdffx0r80W4sSoOKSMECiOAT9Lvl4Rs2SMgiIgLp5iuEA899JDFIo4PHxFuuuqarMkAAo5cv/nmG2vtvHnzzCqrrGJuuummDFhf2MROnTqZzTffvHDACoQQ4VYAdGUpBGqLQMOGDS3BQrrt27c3/fv3r22SqYg/duxY27vloRRHEeHGsVSkkxAogACDQV27drVEy6R+19stEC3Vt7///nvTrFkzs/fee8fWThFubItGigmB3AjgRsBnS0+X3xJjTj31VIvJ66+/Hls4RLixLRopJgRyI+D8uP7Bs9wx0n3nzTfftGR70kknxdpQEW6si0fKCYHqCLhBMvy29HLlTjBm3333NU2aNDHffvttdcBidEWEG6PCkCpCoBgE8Nm6QTI3eFZMvLSGeeCBB+yD56qrroq9iSLc2BeRFBQCfyHAYJl3kAziZZZClqVDhw6GIwkiwk1CKUlHIWCMnQZGj9a7uMH5crM6cDZ69Gjbu6WXmwQR4SahlKRj5hGAZHMtboCE47iqqtyFhr8Wvy3+26SICDcpJSU9M40APdlcpMoKsyyuMmNGAoOGzFBIiohwk1JS0lMICIFlCDDXFrJl7m2SRISbpNKSrkJACFgEWE3GqrIlS5YkChERbqKKS8oKgf8h8PDDD5s+ffrYZawTJ07MFCz33Xef7d2yb0LSRISbtBKTvplHgO9z8TrtPS677LLM4MJOYOwIlkQR4Sax1KRzphHo0aNHFbKFeNdaa61MYMLAIfay520SRYSbxFKTzplGgB6et3fL7zp16qQeE77ewNQ4vuaQVBHhJrXkpHdmETj77LOrEe5+++2XejxYZcfDZfbs2Ym1VYSb2KKT4llGoF+/fstId6eddjLz589PNRyvvfaatZcv8SZZRLhJLj3pnmkELrroIktCP//8c+pxYBvK5s2bmx9++CHRtopwE118Uj7LCLC6jFfstPdu3ayMcePGJb64RbiJL0IZkFUE3MY177zzTqoh2GyzzUznzp1TYaMINxXFKCOyiMBTTz1le7gzZsxIrfkjR460Nk6bNi0VNopwU1GMMiKLCLj9BFh1lkZZvHixadCggendu3dqzBPhpqYoZUjWEPj4449t72/SpEmpNH3gwIHWvjS5TES4qayqMioLCLAfLINmV199derMnTlzprVt8ODBqbJNhJuq4pQxWUPg73//uxk2bFjqzN5tt91My5YtTdqmvIlwU1dVZVCWEGjcuHHi9oQtVD5333237d2OHz++UNDE3RfhJq7IpLAQ+AuB1q1bmyOOOOKvCyn41bZtW9OlS5cUWFLdBBFudUx0RQgkBgG+VturV6/E6FtI0REjRtje7aOPPlooaCLvi3ATWWxSWgj8D4Fu3boZjjTIwoULTb169ezG6mmwJ8gGEW4QKromBBKCAF+spZebBhkwYIDt3c6ZMycN5gTaIMINhEUXhUAyEMB/ix836fLyyy9bsh0yZEjSTcmrvwg3Lzy6KQTijQBfrW3SpEm8lSxCu549e5pWrVqZpUuXFhE6uUFEuMktO2kuBAxbNDIXN8kyefJk27u97rrrkmxGUbqLcIuCSYGEQDwRYJUZq82+++67eCpYhFZt2rQx22yzTREhkx9EhJv8MpQFGUaAfRQgXPZVSKLwtWH0nz59ehLVL1lnEW7JkCmCEIgPAuwUBmGxc1jSZMGCBaZu3bqGzwVlRUS4CS/pefPmmUMOOcQ2OhoeB/+/+eabhFsm9YtB4IUXXrBl/vTTTxcTvGJh+vbta/x72h5zzDFW97lz51ZMr6gzFuFGjXiI+bEBNZ+N3m677Qy/OfjsSsOGDU3Xrl1DzElJxRUBti7kIcvXH+IqTPnadNNNrZ59+vQx77//vnnxxRftf75AnCUR4Sa0tOnZQrb9+/evZoH7EgDkK0k3AnzPDMJNQlnjr11ppZWsvuutt55Zc801zW+//ZbuAvJZJ8L1AZKUvxDtWmutlVNderlDhw7NeV830oHATz/9ZAls1KhRiTCIB8QOO+xgdW7WrJm55ZZbEqF3WEqKcMNCMuJ06NXka2S4GTgk6UdgxRVXjOXD9ZdffjHs/HXPPfdUKYSNNtrItGvXzmy//faWeLt3725dDFUCpfSPCDeBBetcBrNmzcqpPWQb5G7IGUE3EovAaqutZk444YTY6c+OX3xtl87BXnvtZWdSXHzxxfb/E088YfW94YYbzBprrGGv3X///bGzIWyFRLhhIxpBevRsqcT5hPtyKeRDKD33Nt54Y3PwwQfH1qCxY8eapk2b2jq7/PLLG2YseIXlvGeeeab3Ump/52+1qTU72YZBpPkIl54v9+M8cp3sEoiX9ltttZXZY4894qWUTxu+v+ZmKuC7TePXHHwmB/4V4QbCEu+LECmEykyFICk0oBYUR9eSi0CPHj3MtttuG2sD3Hzho446yvC9Muovy3mdayHWyoeonAg3RDCjSsr1YINcBs6/G3QvKv2UT7QIHHjggbb3GG2upeW28847m7XXXtv88ccfNuKdd95pNtxwQ0NvN8n7QJSGgjEi3FIRi0l4erHMw73yyittT5fe7nnnnZdzbm5M1JYaZUDguOOOswNPZUg6lCRvu+0226MNmis8ZsyYUPJISiIi3KSUlE9Plu4OGjTIVmRezzg099YHUkb+sml3/fr1Y2vt+uuvb6eAxVbBCBUT4UYIdrmywo3gerzaQ6FcKMc33eHDh9sHbhxXbbFfL50B6qhELoXU1AGIlpVn2kMhNUVatCETJkywpLZo0aKi40QR8LPPPjMrrLCCOfTQQ6PILhF5qIebiGIqTkl6ESx40HSw4vBKS6i7777bEi6bwsRJ+N4aX6PINZsmTrpGpYsINyqklY8QKBMCbN7Na/srr7xSphxKT/bZZ5+1Op1//vmlR05xDBFuigtXpmUDgZkzZ1pye/zxx2NjcLdu3VLxNeGwARXhho1oBdLjlY2J5X/++WcFcleWlUbggw8+sITLxxjjIOwARo974sSJcVAnVjqIcGNVHKUrw8odKjfHqquuKv9t6RAmPsbixYtt+V977bWxsKV169aGHq6kOgIi3OqYJOYKPQhHtu68+uqrJ0Z/KRoOAr///rutB2zwXWm54IILrC7PPPNMpVWJZf4i3FgWS3FKHX744dUIF+J97bXXiktAoVKDQIMGDSq+4xZfDmY3MOqlJBgBEW4wLom42qtXr0DCXbhwYSL0l5LhIcDnavgoYyWF+bbMu/30008rqUas8xbhxrp4gpVjkYP7Um+dOnWqkO7AgQODI+lqqhHgCwq9e/eumI18NZi3qwsvvLBiOiQhYxFuEkrJoyMj0S1btrSVG5/d559/bjetOeyww8ytt97qCamfWUKABZLObsoAAA47SURBVC+77LJLxUzmcznsmSDJj4AINz8+sbm7ZMkS6xujF8HyXflpY1M0kSvy448/mo8++sjWAfaTnTJlimnfvr1d2n3WWWeZAQMGGD5H3rNnTzN79uyy63fzzTfbDoAe+IWhFuEWxqjiIfgIHz46yJZvQkmyjQCb1FAXgg4+Q96iRQvTpk0b06VLF/P888+XFSzmfq+zzjpmp512Kms+aUlchBvjkqQnc/TRR9uGxY7+rCiSCAEQYI/Zhx56yC54eeedd8yRRx5p52FHjY773FO5iT1qu8qVnwi3XMjWMt377rvP9hzoxTC3USIE8iHA5vMMoEYpuDWWW245S/ZR5pvkvES4MSu9X375xbCDP0TLK+FLL70UMw2lThwR4Msf1BneiqIS9mCG5Bm4lRSHgAi3OJwiCfXggw+a9dZbzzYcfZMsEshTk4kbuPriiy8isenJJ5+09XTYsGGR5JeWTES4MShJlmYyf5YeypZbbln2gY4YmCwVQkbg/vvvt/UnilkJqM40ND4CKSkNARFuaXiFHnratGlmo402so3l7LPPDj19JZgNBNi7gAd2FINXN9xwg83r9ttvzwa4IVopwg0RzFKTOvHEE23F7dChg9FmH6Wip/BeBN544w1bl5i5UE7hbYxPOXXv3r2c2aQ2bRFuBYr2scceM5tssoltIIMHD66ABsoybQiwfwE9XKaLlVPOOeccm8+MGTPKmU1q0xbhRly0p556qq2wrAxi4EEiBMJAgJWIEO6YMWPCSC4wDbfROXPDJTVDQIRbM9xKjsUSzM0228w2itNOO63k+IogBAoh8I9//KOsm8ccdNBBhpVs8+fPL6SK7udAQISbA5gwL59xxhmWaDfddFPDB/8kQqAcCDRt2tSccsop5Uja1lt60JdeemlZ0s9KoiLcMpY0W9ZtscUWlmxPPvnkMuakpIWAsXO42TWuHMLS8o033rgcSWcqTRFumYp7yJAhlmippI888kiZclGyQuAvBDp27Gj22Wefvy6E9GvChAm2Lt95550hpZjdZES4IZf9c889Zzp16mQr6KBBg8wff/wRcg5KTggEI8COXTvssEPwzRpe/fXXX02rVq3sVo81TELRPAiIcD1g1Pbnueeea4l2gw02sDs51TY9xRcCpSCw3377WRdWKXEKhWV/XXy32tOjEFLF3RfhFodT3lDMSezcubOtmGz+vHTp0rzhdVMIlAMBtmhkb9qw5P3337d1ms2UJOEgIMItgCO7ML3wwgs5Q51//vm2UrZu3dqwnl0iBCqFwOmnn24aNWoUWvZ9+/Y1K6+8svnyyy9DSzPrCYlw89QAeqrs3kXv1S+vvPKK2XrrrS3Z8rXUn376yR9E/4VApAjwNRD2pw1DWA2JK2H48OFhJKc0/h8BEW6BquB2YaIn6+Siiy6ylZE15XxPSiIE4oDAuHHjbL3kq861FfZibtu2bW2TUXwfAiJcHyBBf4899lhbkW+55Ra7LR1Pfvxl33//fVBwXRMCFUGA3buom/PmzatV/tdee61N56677qpVOopcHQERbnVMql1hF318Y1RmpsioIlaDSBdigADzvamjtfmiM18cadmypdltt91iYFH6VBDhFijT119/3c5tpCJzaM/aAoDpdsUQePHFF20drc2mSGeeeaZNgzEKSfgIiHDzYDpixAhb+fjs9B133GHdCJDuq6++mieWbgmByiDw7rvv2vp677331kgBF//444+vUXxFKoyACDcAIz5TwqodyPXggw82ixcvtqG+++47s8Yaa5iuXbsGxNIlIVBZBJi+RZ298cYbAxX55JNPAq+7i7179zYNGjQwixYtcpd0DhkBEa4P0CuuuMJW2mbNmplbb73Vd9eYyZMn2/vaNakaNLpQYQTwv0K4I0eODNQEIsbtECTO/3v55ZcH3da1kBAQ4f4/kLxO9ejRw1ZYJnwvXLgwJ8SsvKFyS4RA3BCoW7eu4asMQcL4Q65FDMw1Z79mSXkREOEaY6666iqz/PLLm8aNGxs+Ny0RAklFgBkGbJ7EbnXnnXeeocd600032fniRx11VKBZ11xzje1o3HPPPYH3dTE8BDJNuKwVZ/oLr2EHHHCA+eKLL8JDVikJgQog0KZNG7P//vubr7/+2vZm586da90IuMDYupFPPPHdM64jTHlcbbXVzB577FEBbbOXZWYJ9+qrrzZ16tQxDRs2NHz2WSIE0oAAK8SC5tAyd/zxxx83X331lT2zcnLUqFGGDcvpcGjmTTSlnznC/fDDD82ee+5pK1mvXr0MXzuVpBOBp556yvDVDY4wlrsmAaVdd93VbLPNNtVUpYfLRyC9wobikO0JJ5zgvazfZUQgU4Q7fvx4w6BCvXr1DMsXJelEYNasWWbttde2ZMIbDKTCAQGnXRjw9e+BwCZM7Any559/VjEf18Mqq6xie71VbuhP2RDIBOEy/3Dfffe1jW7vvfeu9VrzspWGEq41AvRkIdvtttuuSq+WgaMsCPsxs/y8kDz88MO2PTANUhIdAqknXL7HVL9+fbPiiisadlOSpBsBerFZ6c0GlSRTv9jDtpBsueWWpn379oWC6X7ICKSWcD///HM7WkvjYwTWjcqGjJ+SixkCWSdcpoFR5/N9dWTs2LE2zNSpU2NWeulXJ5WEy4oafFMrrLCCGTNmTPpLURYuQwCXAn5bem+13aZwWaIJ+nH99ddbMs21cIctRVlFuddeeyXIqvSomirCXbBggTnwwANthevZs6d577330lNSsqRoBBg0Y3N4enpM/s+SsHgBu+fMmRNoNvNwuQ9GkugRSA3hsjl406ZN7SdGmFsoyTYC9HSHDh1qyeWQQw7JDBhPPPGEtTnoK7tvvfWWvXfiiSdmBo+4GZp4wmVno379+tmK1L17d8M+nlSo+fPnxw1r6VMBBJjcn6UeHQsYsPfRRx+thjbzzlm+npU5ydUAiMGFRBPupEmTTPPmzW0F8+5yNG3atMCdvmKAt1SIGIGsDaKxsAfCZVGDVx544AF7nX1DJJVDIJGEyzpxXhOpWDvuuKN54403qiDIF3QHDhyoJ3kVVLL5x7kVstKrY+ku7YJFPl7p0KGD2WKLLbyX9LsCCCSOcHlysyMSleqyyy7LCRm9X9aOI0wJo9crSTcC/fv3t+4kdny78sorlz2UId2sCKvJaBuXXHLJMpNHjx5tr7HaTFJZBBJDuHxt4fDDD7cVhy8u5PtQ3u+//26YY8iMhcGDB5uLL77Y8EolSTcC+GtZYcYMBc7smZGF5bz+UmVa3BlnnGEv026aNGlidwrzh9P/6BEoK+HypPUeEGVNpqMw1WXNNde0aUGe+YQ9EnAn4KtiOe9HH32UL3hi7zEoSA/euxH69OnTU2tvYguqAoqztPnoo4+2OZ988sm23fjdbhVQS1kaY8pGuG6wgp4mvzm3a9fOLkgoFvkffvjBsGkypL3tttuamTNnFozKdBjiISx6ePPNNwvGSWKAiRMnWly8szHYRH3YsGFJNEc6h4gAiz7Y35kvTtN2TjnllBBTV1K1QaBshMvrHa82XnEknOs1j82QnUDQ66yzjq0wF1xwgbtc0pmvlwZNjykpkZgGFuGGVzDuI6HhpVjZlHiT7Natm3UjMDcdt4IkHgiUjXAZwMCP5pVchMvqF7ZN5GmM381tisxmykETuL1p5vv93HPP2d3t84VJ6j0Rbu1LDgxbt25t6x1vX2kYWD333HPtknbnysvaSrva14ryplA2wmXgwj86PGjQoGq9Xjcx3VUQd/bHrQkMvFL5p8fUJJ04xhHh1q5U3n77bUu0rr5xZv8N9hpIqjA7w2sPv+npSuKDQFkIlzmPFDZPV3bbpyLwmoOLwb8v6fbbb1+tkhB33XXXtb0PeiA1PRho45WqpvHjHG/VVVe1uDFA4vQEN1YSuf8656471Avw8h+4spIq++23XzV7sC/Xl3qTameS9S4L4TrXgbcy42II2r3Jfe7GG5ZdvpgCpiM3BrhrwIypbw6n5ZZbznTs2HHZf3dd5+o48hkab51zv5npkVRxrjhnizsvWbIkqSalTu+yEC7uAFwKTiBVCDdIpkyZUq3ia1Q1CKmq1+RSqIpHqf++/fZb06JFiyp1j9VYSRa3cY0jWs5HHHFEkk1Kne5lIVwIlsMJbgQKP9fySr4o2qNHD7P11lub4cOHu2g650FAhJsHnCJvzZ4923YEmEbFp2nY3jPp8uCDD9oN9zt16mRqOrsn6RjEWf+yEC6+Wu+gl/Pp+v23cQYm7rqJcONeQtJPCFRHIHTCxU9Lb9Y/15YeLwNnknAQEOGGg6NSEQJRIhA64TLKG+Q+cG6FoIGzKA1OS17sF8GyXu+nr/nPdYkQEALxRCB0wo2nmdJKCAgBhwD7mdAp8nd+cP0xF5n58pLyICDCLQ+uSlUIxBqBoDnxzCRidlGuwe1YG5QQ5US4CSkoqSkEwkTAP1XTzZ33j72EmafSKuNuYQJXCAiB+CLAknpWKSL0aPktV0L5y0s93PJjrByEQOwQ8PpxIVo275ErofzFJMItP8bKQQjEEgH8uJAtA2g1+TBALI2KuVIi3JgXkNQTAuVCAD8uZOtdpFSuvJTu/xAQ4aomCIGMIuDf8ySjMERqtgg3UriVmRCIDwL0cDkk0SEgwo0Oa+UkBGKFgH/Pk1gpl1JlRLgpLViZJQTyIZBrz5N8cXSv9giIcGuPoVIQAolDgFkJbGKvqWDRFp0IN1q8lZsQEAIZRkCEm+HCl+lCQAhEi4AIN1q8lZsQEAIZRkCEm+HCl+lCQAhEi4AIN1q8lZsQEAIZRkCEm+HCl+lCQAhEi4AIN1q8lZsQEAIZRkCEm+HCl+lCQAhEi8D/AWLOQZtc0B8wAAAAAElFTkSuQmCC[/img][br][size=150]Here are some statements about 2 zigzags. Put them in order to write a proof about figures [math]QRS[/math] and [math]XYZ[/math].[/size][br][list][*]1: Therefore, figure [math]QRS[/math] is congruent to figure [math]XYZ[/math].[/*][*]2: [math]S'[/math] must be on ray [math]YZ[/math] since both [math]S'[/math] and [math]Z[/math] are on the same side of [math]XY[/math] and make the same angle with it at [math]Y[/math].[/*][*]3: Segments [math]QR[/math] and [math]XY[/math] are the same length, so they are congruent. Therefore, there is a rigid motion that takes [math]QR[/math] to [math]XY[/math]. Apply that rigid motion to figure [math]QRS[/math].[/*][*]4: Since points [math]S'[/math] and [math]Z[/math] are the same distance along the same ray from [math]Y[/math], they have to be in the same place.[/*][*]5: If necessary, reflect the image of figure [math]QRS[/math] across [math]XY[/math] to be sure the image of [math]S[/math], which we will call [math]S'[/math], is on the same side of [math]XY[/math] as [math]Z[/math]. [/*][/list]
Take turns with your partner stating steps in the proof that figure ABCD is congruent to figure EFGH.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWgAAADpCAYAAAAJfq0cAAAgAElEQVR4Ae2dCbQUxRmFQZYYZFExnBhkCUbUCGFJNCgoIoFIRBDcEBVcooKooAExoLKLioAIiKL4BBUQXkRUXIJHCITkYAybxiWoIBAVRQgqhBDwz7mV1Nivp6enZ6bX6lvnzOuerupavqq+75+q6qpKQkcCJEACJBBLApVimStmigRIgARIQCjQbAQkQAIkEFMCFOiYVgyzRQIkQAIUaLYBEiABEogpAQp0TCuG2SIBkwgsW7ZMJk+e7FiksrIyWbRokaNf2i9SoNPeAlh+EgiBQN++faV9+/aOKTVq1EhGjBjh6Jf2ixTotLcAlp8EQiDQokULRxHetGmTVKpUSWBh02UToEBnM+EVEiABHwns2rVLibBTNwauQaDpnAmQjDMXXiUBEvCJAKxjiDCsZbtD1wasazpnAhRoZy68SgIk4BMBiDAEeuTIkVmfxo0bC/qn6ZwJUKCdufAqCZCATwS6d+8uGAjEIKH9A+HGLA46ZwIUaGcuvEoCJOATgTp16jgOEK5du1ZZ1jjSOROgQDtz4VUSIAEfCLjN0oDlzAFCd8gUaHc+9CUBEiiBgNssDbe50SUkadStFGijqpOFIYF4EXCbpYHZGwMHDoxXhmOWGwp0zCqE2SEBkwhgUDDXLA10bzjNjTap/KWWhQJdKkHeTwIkkJMA5kA7zX/Gyyvww5EuNwEKdG429CEBEiCBSAlQoCPFz8RJgARIIDcBCnRuNvQhARLwkcCsWbOkQ4cO0rZtW5k0aZKPMZsbFQXa3LplyUggNgRmzpyp5jxjYFB/uMRo/uqhQOdnxBAkQAIlEmjXrl1GmLVAH3PMMSXGav7tFGjz65glJIHICbRu3TpLoGvXrh15vuKeAQp03GuI+SMBAwiMGzcuS6D79+9vQMmCLQIFOli+jJ0ESOD/BIYOHSqVK1eWatWqyXXXXUcuHghQoD1AYhASIIHSCezYsUNZ0TNmzCg9spTEQIFOSUWzmCQQNQG9vOiSJUuizkpi0qdAJ6aqmFESSDaBxYsXKwt6w4YNyS5IiLmnQIcIm0mRQJoJTJs2TQk019/w3goo0N5ZMSQJkEAJBDBIiN1V6LwToEB7Z8WQJEACJRDo3bu3NGvWrIQY0ncrBTp9dc4Sk0AkBE4//XTp0qVLJGknNVEKdFJrjvkmgYQRaNy4sVx77bUJy3W02aVAR8ufqZNAaggccsghMmbMmNSU14+CUqD9oMg4SIAEXAls3bpVzeCYPXu2azh6ViRAga7Ig99IgAQCILBq1Sol0K+99loAsZsbJQXa3LplyUggNgTmz5+vBHrjxo2xyVMSMkKBTkItMY8kkHACEyZMUAK9b9++hJck3OxToMPlzdRIIJUEbrrpJvn+97+fyrKXUmgKdCn0eC8JkIAnAj169JCTTz7ZU1gG+pYABfpbFjwjARIIiMBPf/pT6dmzZ0CxmxstBdrcumXJSCA2BOrVqyeDBg2KTX6SkhEKdFJqivkkgYQS+Ne//qUGCCdOnJjQEkSXbQp0dOyZMgmkgsB7772nBHrBggWpKK+fhaRA+0mTcZEACWQRePXVV5VA//nPf87y4wV3AhRodz70JQESKJFAWVmZEuht27aVGFP6bqdAp6/OWWISCJXA6NGjpWrVqqGmaUpiFGhTapLlIIGYErjmmmvkhz/8YUxzF+9sUaDjXT/MHQkknsAvf/lLOeOMMxJfjigKQIGOgjrTJIEUEfjxj38sl112WYpK7F9RKdD+sWRMJEACDgRq1aolv/3tbx18eCkfAQp0PkL0JwESKJrAF198oWZwPPjgg0XHkeYbKdBprn2WnQQCJrBu3Tol0M8//3zAKZkZPQXazHplqUggFgQgzJUqVRIINV3hBCjQhTPjHSRAAh4JoGsDAo2uDrrCCVCgC2fGO0iABDwSwOAgBgnpiiNAgS6OG+8iARLwQODSSy+Vk046yUNIBnEiQIF2osJrJEACvhDACypnn322L3GlMRIKdBprnWUmgZAI4BVvvOpNVxwBCnRx3HgXCZCABwJYJAmLJdEVR4ACXRw33kUCJJCHAJYXxQwOLDdKVxwBCnRx3HgXCZBAHgJYoB8CjQX76YojQIEujhvvIgESsBHAnoNz586VlStXyubNm2X+/PlKoLHlFV1xBCjQxXHjXSRAAjYCTZs2VYIMq9n6adOmjVx88cUyePBgmTJlijzzzDO2O/k1FwEKdC4yvE4CJFAQgQMHDsimTZtkxYoV8uSTT0rbtm2lRo0acu6550rLli2lbt26SrjLy8sLijfNgSnQaa59lp0EfCKwfft2taQoXu3G+htYe6Nr167ys5/9rEIKX331lezevbvCNX7JTYACnZsNfUiABDwSeOONN9Qr3dauDZxjmh0W7MeuKpgPjSl3EHM6bwQo0N44MRQJkIAHAjt37pT169crK7p27drKgsZuKu3bt5cmTZpI9erVPcTCIJoABVqT4JEESKBoAjNnzpTrr79exo8fr/qfMbUOFvQ999xTdJy8UYQCzVZAAiRQMoEhQ4ZIgwYNKsze0N0d9evXF8zkuOiii+Q3v/lNyWmlKQIKdJpqm2UlgYAJfPPNN2oONKbTQaBhVd9www3SrVs3adWqlfTp0yfgHJgVPQXarPpkaUggFgRmz56tBHrr1q2xyE9SM0GBTmrNMd8kEGMCY8aMkSpVqsQ4h8nIGgU6GfXEXJJAoghce+210rhx40TlOY6ZpUDHsVaYJxJIOIEuXbrI6aefnvBSRJ99CnT0dcAckIBxBJo1aya9e/c2rlxhF4gCHTZxpkcCKSBQp04dGTp0aApKGmwRKdDB8mXsJJA6Art27VIzOKZNm5a6svtdYAq030QZHwmknMCGDRuUQD/33HMpJ1F68SnQpTNkDCRAAhYCS5YsUQK9du1ay1WeFkOAAl0MNd5DAiSQk8CMGTOUQO/YsSNnGHp4I0CB9saJoUiABDwSGDZsmNSsWdNjaAZzI0CBdqNDPxIggYIJXH755XLiiScWfB9vyCZAgc5mwiskQAIlEDjzzDOlc+fOJcTAWzUBCrQmwSMJkIAvBI499li5+uqrfYkr7ZFQoNPeAlh+EvCZQLVq1WTUqFE+x5rO6CjQ6ax3lpoEAiHw8ccfqxkcjz32WCDxpy1SCnTaapzlJYEACaxevVoJ9NKlSwNMJT1RU6DTU9csKQkETmDhwoVKoN99993A00pDAhToNNQyy0gCIRGYNGmSEug9e/aElKLZyVCgza5flo4EQiVw8803y/e+971Q0zQ5MQq0ybXLspGADwQKWVPjggsukNatW/uQKqMAAQo02wEJkEAWgbKyMrVlFXbm1h9sYTV58uSssNYLP//5z6V79+7WSzwvgQAFugR4vJUETCTQt29fwYL7I0aMkGXLlqki4ghxXrRokWuRjz76aLnxxhtdw9DTOwEKtHdWDEkCxhOAKEOcC+nW0FD279+vrO17771XX+KxRAKBCjT+E+O9fDoSIIH4E9i0aZMSWIh0Me6DDz5Q98+bN6+Y23mPA4HABBo/ifCfGP1XdCRAAvEngC4MPK/YsqoYt3z5cnX/H//4x2Ju5z0OBAJTzxYtWqg+LFS47sdySJ+XSIAEYkKgffv2WQN8sKohvPrjltU5c+YogV6zZo1bMPoVQCAQgcYIMKxnvXkkBbqAGmFQEoiIgB4YtCYP0dazOPL9Gh43bpxUrlxZbr/9drnzzjvVgOJnn31mjY7nBRIIRKAbNWqkrGfkxanSC8wjg5MACYRAAAKcq/8Z40kQazfXr18/adiwoQqybds2JdADBw6UZ599Nus2LKpEl5+A7wKtR4F1PxYqNVel588eQ5AACYRFAIYVhNjJWY0uJ39cO+ecc6Rt27YVvHfv3i2PP/64TJw4UXbu3Kn8Vq1aJWPHjpW9e/dWCMsv2QR8FWiI8uGHH15hMjsEOt9/3uxs8QoJkEDYBCDOeH61caXT112V+eZAN2/eXC655BJ9W4Xjyy+/LGPGjJEFCxYog+2jjz6q4M8vzgR8FWhYytb+Kn1OgXaGz6skECcCEGJ0SeKNQVi9emDwiiuuUM+1XbjteYe433rrrfbLme9DhgyRHj16CKxqOm8EfBNo6xxKDArqD/4r5xtc8JZVhiIBEgiaAEQYzyy6NKwGVr5uSoguwk+dOjUri1jZbtq0aUr0H330UXnppZeywvCCMwHfBFpXqj0ZCDUF2k6F30nALAJvvfWWes6dBgRxTV/fvn27YODw66+/VgAg3lu2bDELho+l8UWgtQjjaHdufvaw/E4CJJBMAi+++KIS6L/+9a95C/DEE08oi3rmzJkyYMCAjHjnvTGFAXwR6HwDgbCgncQ7hbxZZBIwksDDDz+sBPrzzz/PWb4333xT8DIL+rSx4t2f/vQn2bdvX87w9OByo2wDJEACJRIYNGiQ1KhRQ72kghdUcjlMtYOh9s9//lNuueWWTDdHrvC8ToFmGyABEiiBAPqT9WCiPt599915Y7zvvvvk/fffzxsu7QF86eJwgoifM1h+kI4ESMBcAkcccUSWQHvZUeWhhx6S9evXmwvGp5L5LtDoY6pXr56qtEMPPVQmTJjgU1YZDQmQQNwI1K9fP0ugjzrqKNW/7JbXBx98UDZs2OAWhH5+b3n16aefqn4o/VNHH1evXk3YJEACBhIYPnx4lkDXqlVLXfvVr34lmN3h5MaPHy+bN2928uI1CwFfLejy8vKsyoJIc4cFC3GekoBhBO666y5p1aqVYD9CvJBy8OBBeeCBB6Rp06ZKD0477TSZO3duptTwv+GGG+Tf//535hpPnAn4KtBYqFtbzdYj5j3SkQAJpI8AujxPOeUUpQsnnXSSoGsDL7VMmjQpfTCKKLGvAo30saKVVZybNGlSRLZ4CwmQgEkEFi9eLJ07d1bagIHFa665Rr788kuTihhIWXwXaOQSW+f06tVLDRZyT8JA6o2RkkAiCfzhD3+Qiy66SAn1YYcdJkOHDpWtW7cmsixhZDoQgdYZnzVrlqqIJUuW6Es8kgAJkICaYgcrWv/avu666wRTc/O5bt26ycKFC/MFM8Y/UIEGJfQ7dezY0RhgLAgJkIB/BLAuNJYhxZuIEGv88l65cqVjApgNhjBp6r8OXKC1Ff3CCy84QudFEiABEsDr39jT8Oijj1YifPbZZ8vzzz9fAUyfPn2kbt26FV6AO/XUUwVvJZrqAhdogKMVbWrzYblIwH8C06dPlxNPPFEJdZs2beTJJ5+U9957T323rkuNrlNY1CbPEgtFoGlF+9+IGSMJmE4AwgwLGSKMmR+HHHKIWFfL69Klixx//PFGYwhFoEGQVrTR7YiFI4HACECoIdL4oAsEG86+8sor6rvTDi6BZSSCiEMTaFrREdQukyQBAwjccccdSoznz5+vBhEh1FWqVBFM0zP9dfHQBBrtBFb0WWedZUCTYRFIgATCIIAF/dG9gUX+tcP2WdqixhHT9datW6e9jTqGKtC0oo1qOywMCQROADM0IMJ/+ctfMmn169dPsFLm3/72N7ntttukZs2aKsyFF14oeBHGJBeqQANcs2bNaEWb1IJYFhIIkMBVV10l5513XiYFvHUIwR48eHDm2ldffSXYJOCYY45Rfp06dRK8Wm6CC12gH3vsMQWR86JNaD4sAwkET2Dnzp2ZRPBqOAQ6V9/zjBkzlBGIMFikafbs2Zl7k3gSukADEq3oJDYV5pkEoicwatQo+fWvf503I/PmzZN27dopMceyp1OmTFHLoOa9MWYBIhFoWtExawXMDgkYSuCll17KrLCJnZ5Gjx4tX3zxRWJKG4lAgw6t6MS0EWaUBBJNAHujYgBRr6JXvXp1tav4hx9+GPtyRSbQtKJj3zaYQRIwgsDatWvVTi8ozNtvvy0DBgxQXR/op8Yg5Jo1azLlxLZ9ixYtqnAt4xnBSWQCjbLSio6gxpkkCaSMAOZNo6vD6j7++GMZNmyY1KlTR4n1+eefr6xqiLb+XHrppdZbIjmPVKC1FW1ftSoSEkyUBEjASAJ4/+KNN95wLNuePXvUnqkNGzbMCLMWaByjngUSqUCDGK1ox3bDiyRAAj4RwD6I+TYDWLFihaNA9+/f36dcFBdN5AJNK7q4itN3bdq0Se6//37B1mL4YFL/448/rr15JIHUE8DypehXXr58udpdfMuWLVlMPvnkE0eBjnoxpsgFGqRoRWe1F08XysrKVKNq1KiRYJ1cfPr27Svdu3f3dD8DkYCpBJYuXSoQ5uHDhwu2ycKWWpgbDZH++9//nlVsWNBVq1atINJYi/rgwYNZYcO8EAuBphVdeJVrccYGvXQkQAIVCWCdjg0bNsiOHTvk9ddfl0ceeaRiAMs39E8feeSR0qJFCykvLxe8DBN137POXiwEGpmBFd2hQwedLx5dCOzatUsOP/xwGThwoEsoepEACYDA7t27ZdCgQXLgwIEsIBByrOFx3HHHCboL4+ZiI9C0or03DVjNmB4EoaYjARLIT2DmzJlZK91BkPEaOAQaQh1HFxuBBhxa0d6aCH6KsZ/ZGyuGIgEQ2Lhxo+qPxluFcNu3b5eWLVuqrg3rUqZeaUHcR44cmfVB16OfLlYCTSvaW9VifqZ180xvdzEUCaSbwNNPP602oMXypNjrEGtKF7t+NH7F4jls3759hY/RAo3mQyva/SHCf240DEwboiMBEiiMwMSJE9VgIJ6hl19+ubCbLaExWwriHLSLlQWNwurZCXy7MHfVo3Fx9kZuPvQhgVwEsBM4np9nnnkmVxBP19HNGMav2NgJNOg0b96cMzpcmgkGCPFSCh0JkIB3Ano1O+wSXorD4HxYv2JjKdC0ot2bj+7/wiCF1S1btsz6leckQAL/J4BNZyGqbvOhvcLCc4a4wpiWF0uBBiha0e7NBT+v0EjwwZxofe5+F31JIH0Err/+evV8YFcVP5z12dPPHY5Y1tRvF1uBphWdv6rxUwv/zfWH86LzM2OIdBHA5rIQz/Hjx/tWcExxxQChfu700bcELBHFVqCRR1rRlpriKQmQQEEE7rjjDiXOOPrp9No3fsaZK65YC7S2op977rms/OP9ejoSIAEScCIAixmWMyxoP52e5gqrOQwXa4EGALsVjaU1sbh2r169wuATehrz589XK2+NGTNGsOsDHQmQQGEE0NcMcUbfs98O7x8g7rC6E2Mv0NqKxlbretcD9AEV+waQ3xXmZ3y33HKLqnw0AHzq168vW7du9TMJxkUCRhPAmht4djBrIwiHAUJ0cYTlYi/QsJirVaumoJsqzKhsbAWvhdl6vPPOO8NqC0yHBBJNAPOb8excfPHFgZUDBiM+YbnYCjSEuUGDBgp469at1dGpLzosUEGng7VrrcKsz7koUtDkGb8JBPBmIJ6Zc88914TiZMoQS4Hu1KmTgo3tm7DTARz6ok1/e846n1kLNI74uZZvT7VMjfKEBFJGAGtq4Dnp2LGj45rPScYRS4HGFulamDVc3RdtqhWNrgw0slq1aqkjzq+66ir1vr++BqGGpU1HAiTwPwIYi8KqdKeddppglTrTXCwFOhdkU61oLc56ShDWp922bVsGA3aEwOAEhTqDhCckIHhOsFUV1nXG+s4mukQJNHarhmVpkhWtxXnIkCF529eXX35Joc5LiQHSQAA7oGCWE3ZECWNNjKiYJkqgAckkK1q/6eRFnK0NRAv1YYcdpv5hsevDSofnphP48MMP1R6Ccd6qyq86SJxAm2JFFyvO1orH4uNYOJxdH1YqPDeZwKeffqoW3K9bt65gN27TXeIEGhXyk5/8JNEzOvwQZwykTp06VbVPWNRYepRCbfrjmu7yoZ23adNGvvvd72ZNIjCVTCIFOslWtBZnbAPv5DDYsWXLFuW1Z88ewT6Ne/furRAU6wBg0ND+uqkW6tq1a6uuD1jXnPVRAR2/JJTAf/7zHznrrLNUuy5lq6qkFT+RAg3ISbSitTj37NlTCew777yT1V7wE2706NGZ6xBo62vtv/vd72Ts2LHyySefZMLYTyjUdiL8nnQCXbt2VeKctr04EyvQ2opevHhxItqeFmc9IIj+s2HDhqldhq1T6rBAEhZK0g4vqNx3332ycuVKJepz5syRffv2aW/Xo5NQr1+/3vUeepJAVAR69OjhuOi93qrqqaeeiiprkaWbWIEGMVjRYeysW2rt2MVZx7d//35ZsmSJDB8+XO655x4pLy9Xm1n2799fVq1apfyw+Mspp5yi/N999119a0FHCnVBuBg4AgIwHJo0aSL16tVTbV9nAd10mFrrx1ZVOs4kHRMt0EmwonOJs72RbNy4UX7/+9/LtGnT5IILLpAnnnhCsLM5LO25c+eKHz/t8KYVBhOtfdS0qO01we9REcAz0KxZM6lZs6a8+uqrAkMF4vzAAw9ElaXI0020QINenK1or+JsbQUYILz77rutl9RbhbCy/XLFCjXWqkYfOR0JBEXgH//4h5x88slSuXJlJc72ZyGodOMab+IFOq5W9O23364amO5z9toANm/erLoz7OEx59nvGRmFCjUeHExzgqNQ22uI3/0ioPcRhPUMoyDNLvECjcqLyoru3bu3TJ48Oav9aHG+9dZbs/zyXcBrq2EPfEKoR40a5dr1MW/ePPUPZ8GCBcqir1q1qhRTvnzlp3+6Cdx1112qnWHzii5duqhzzGRKqzNCoKOyorHaHP7LW0W6FHGOuhFqoa5Tp44qV58+fUT3UVutZ73zC6x9rMMLoaZFHXXtJT99rAGP52nAgAGZwpx//vnq2vTp0zPX0nRihECjwqKyoq0inWRxtjZ6u1CfccYZ6iHR1jMeoptuuknd0q5dO8GGCnQkUAoBvVXVlVdemRXN5ZdfLpdddlnW9TRcMEagw7KiL7nkkqzV9LRIQ7hM+tmvhbpKlSoZixoPC8qprWecY6shOhIolgBmLKEdBblVVbF5i/o+YwQaIIO2or/++mu1Bggak3XJU20547q1uyPqyvUjfd33jJcF9FofJ5xwgqxbt05oPftBON1x4M1YPDfdunVLN4gcpTdKoGfPnq0qO8hBNrtIa3GG5awtafSlmeLQ93zqqaeq4tx4442KrxZqPFgY1KEjgWIIYMEvtKFf/OIXcvDgwWKiMP4eowQatRW0FY00rCKNBmbt1jBJpLX1vHDhQjVzA2VF3zPK37BhQ7F2fcCipiMBrwSWL18u3/nOd4zdqsorh3zhjBPoMKxoQB06dKj67w/RsnZ3wA8ijdHnpDur9WyfuYFyz5o1S03Ps876oFAnvdaDz//rr78uRxxxhLRq1Uo+++yz4BNMcArGCTTqImgrWndr3HzzzY590gluD1lZt1vPCGDve4ZFjRX49K7kmJ5Hoc5CyQsi8tZbb6mtqo4//ng10Ewo7gSMFGhtRT/77LPupRdRay8fOHAgbzgdAK9cW7s1rN0ddkta32PCEdOg8BIN5j2j/E4zN+xCjRkfFGoTat+fMnzwwQfyox/9SBo0aCBvv/22P5EaHouRAo06a9GihWD+bj6HAcUXX3wxXzDlbxdnfZMWaSxyZLqDUOeb90yhNr0VFF4+rF+OX7Zp2aqqcELOdxgr0F6t6BkzZniy8rQ4o+/ZyUGU6CoScBLqtWvXVgzEb8YT2L17t1rDpUaNGmpdc+ML7GMBjRVoMLJb0VjOELuTvPDCC2opz9dee0369esnH330kSvSfOLsejM91awPax81uj4o1OloGNiqqkOHDqpb7JVXXklHoX0spdECra1ozEDA595771VrK2ORfHRroB8VjWfgwIFqHeY1a9ZkoaU4ZyEp+gL2WKRQF43PlxvxjxFjCPZPUBtfnHPOOSotP9Yz9wVAwiIxWqBRF7CimzdvnrXBKvzef/99mTBhgpokj6k/OMfi4FiTFo7irDD4/odC7TtSzxGWlZUpwcTGw9ZPEL9oLrzwQpUWNpygK46A8QKtrWinGR0rVqwQ+z5naLR4GePqq69WjStXn3NxuHmXlQCEGvsvYk4sLDp2fVjpBHOOX4tBWcvWHOutqh599FHrZZ4XSMB4gQYPe1+0ZrR06VJlRejv+qi32qE4ayLBHinUwfK1xo5nASIdpMO4Dv7hpnmrKr/4pkKg3axoO0h2a9iJhPfdLtRYYjKIn97hlSh+KUE40c0RlNNvnGITZLrSCaRCoIEplxVtRThs2DB2a1iBRHROoQ4GPLrv7IOD+O7XCoz6DdsRI0YEU4AUxpoagc5nRVOc49f6nYTaaaZN/HIezxxBiLFuinVwEOe7du0qOcPjxo1T4l/oHpwlJ2x4BKkRaNRjLiua4hzvVk6h9qd+MHAXxAAhhB+WuHWrKn9yzFhSJdBWKxoPPRzFOTkPgReh3rt3b3IKFHJOGzVqJH53Pzz88MNKnLGCI53/BFIl0MBXr169zDrGTZs2VY3rtttu858sYwyMAER47NixcuSRR6r6w2Ai3hDFWiiw5A499FAZNGhQYOknMWJ0Y4CNny+MzJkzR8XZq1evJCJJRJ5TJdBTp05VDQoNVX+OO+64RFQUM5lNwC7Uuk71kTMJvmWmBwixdycWy9cfrFBYjCsvL1fPELeqKoae93tSJdCdO3fOCLN+iHHkQkfeG0wcQ6L+KleunFW3WLea7n8E0LVhbfP6vJguDyyTgPs7deok33zzDREHSCBVAo2NT3XD1EessEWXfAJHHXVUVt1iHQg6fwnA8q5evbq0bduWho2/aB1jS5VAY5EkLcz6OHjwYEcwvJgsAnoOrq5XHPEznM4/AqtXr1a75nCrKv+Y5ospVQINGFhqFIu4YCfhKVOm5OND/wQRmD59uqAbq2fPnr4OhiUIge9Z/fzzz2X//v3y5ptvyg9+8AM54YQT8i7P63smUhxh6gQ6xXXNopOAZwJY6bFjx47qFyd2b8d+k9jJ/Z133vEcBwOWToACXTpDxkACxhHAL0xrdxHOOQYgYlgAAAMqSURBVB01/Go2QqAxVUhPG8KRzgwCmBqm67XY6WBmkAi3FDt27MgSZwh0165dw80IUxMjBLp79+5ZDerMM8/kSmgJbuD6xQqrFYef2SNHjkxwqZKRdexyj5kaVvY4x6vidOESMEKg7a+wYolKrLsBkaZLJgH9YoW2nFGnei5v0OsZJ5OYv7nG7Ca7QPPXqb+MvcSWeIHWlpb9FVb9MHuBwDDxI4D6w8prdqfrVQu33Z/f/SOAHe/xpuCVV16pXqX3L2bG5JVA4gXabmnpguPnGCxrumQSQLeV08prur5xpCMB0wkkXqBhUVmFGA8u+ilhfXE3juQ2X3u3lbUk+OmNeqcjAdMJJF6gYWXZ+8patmwp/Amc3KaLukOdOlnJbn7JLTFzTgLOBBIv0LCUrVv2oC8aA4TnnXeec4l5NfYEUIcQaKedPrQffx3FvhqZQR8IJFqgc1lTfIh9aBkRRmHvtrJmhWMLVho8N51AogUauxPD0rI7PZBEK8tOJhnf0W3lNOdW16v1F1MySsRckkBxBLLVrbh4IrkL82HRnWF3eMCtA4d2f36PNwH807WLML7jRRUn4Y53aZg7EiieQKIFGkLcuHFjNWsDMzewzRG+cwZH8Q0i6jvxqwcCfcUVV6h6xVgC6hTXOHMj6tph+mETSLxAQ6T1Bw8wLC2nwaWwwTK94gigG0PXJ+ZCo07RlcU6LY4n70o2gUQLdLLRM/ckQAIk4E6AAu3Oh74kQAIkEBkBCnRk6JkwCZAACbgToEC786EvCZAACURGgAIdGXomTAIkQALuBCjQ7nzoSwIkQAKREaBAR4aeCZMACZCAOwEKtDsf+pIACZBAZAQo0JGhZ8IkQAIk4E6AAu3Oh74kQAIkEBkBCnRk6JkwCZAACbgToEC786EvCZAACURGgAIdGXomTAIkQALuBCjQ7nzoSwIkQAKREaBAR4aeCZMACZCAOwEKtDsf+pIACZBAZAQo0JGhZ8IkQAIk4E6AAu3Oh74kQAIkEBkBCnRk6JkwCZAACbgToEC786EvCZAACURGgAIdGXomTAIkQALuBCjQ7nzoSwIkQAKREfgvZ7f0ryvSBsIAAAAASUVORK5CYII=[/img]
IM Geo.2.5 Practice: Points, Segments, and Zigzags
Write a sequence of rigid motions to take figure [math]ABC[/math] to figure [math]DEF[/math].
AB=CD
Prove the circle centered at [math]A[/math] is congruent to the circle centered at [math]C[/math].
Which conjecture is possible to prove?
Match each statement using only the information shown in the pairs of congruent triangles.
Triangle HEF is the image of triangle HGF after a reflection across line FH.
Write a congruence statement for the 2 congruent triangles.[br][br]
Triangle ABC is congruent to triangle EDF.
[size=150]So, Lin knows that there is a sequence of rigid motions that takes [math]ABC[/math] to [math]EDF[/math]. [/size][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAASwAAACiCAYAAAD7sPBpAAAdaElEQVR4Ae1dCfgVUxtHylq0WVtESqiEqJA1LSrZixQ9srYQCa2EEC1okyU7ZaflKS0IWbILlSQqiihZ0nK+53e/7z3f+U937p25c+7cmbm/93nuc+6dOevvvPc3Z855z3u2URQiQASIQEwQ2CYm9WQ1iQARIAKKhEUlIAJEIDYIkLBi01WsKBEgAiQs6gARIAKxQYCEFZuuYkWJwP8R+Pvvv5WXz/r169XmzZv/nzDm30hYMe9AVr/4EFi7dq3ab7/9VPny5VWlSpVcPxUqVFDlypVTX375ZWJAImElpivZkGJB4IMPPlDbbLONp892222nMMpKipCwktKTbEfRIDBq1ChNVo8++qiaNWuWmj59+lafadOmqblz5yYKFxJWorqTjSkGBNq1a5cirIoVKxZDc0u0kYRVAg7+IALRR6Bs2bIpwmrUqFH0K2u5hiQsy4AyOyKQTwR+/vln/TrYv3//fBYVybxJWJHsFlaKCKRHAHNVMuE+c+bM9JESfJWEleDOZdOSh8DAgQM1YS1btix5DczSIhJWFoB4mwhECYEmTZqkCKtKlSpRqlZodSFhhQY1CyICwRGQ18HWrVsHzyyGOZCwYthprHJxIvD999/r18EGDRqoXr16qSuvvHKrz8UXX6ymTp2aSJBIWInsVjYqiQg8++yzmrBkpOUWTpkyJYkQ0B9WInuVjUokAj169EgRFrbbNGvWTLVs2VK1aNGixKd58+aqcePGasOGDYnEgCOsRHYrG5VEBGrVqpUirLp16yaxeZ7aRMLyBBMjEYHCIyCvfxdccEHhK1OgGpCwCgQ8iyUCfhBYsGCBnr+aMGGCn6SJikvCSlR3sjFJRWDs2LGasIrRYFT6lYQlSDAkAhFGoH379inC2nHHHdWmTZsiXNP8Vo2ElV98mTsRsIJA5cqVU4RVjB4aTABJWCYa/E4EIoqATLh37949ojUMp1okrHBwZilEIGcE5s2bp+evXnrppZzzSUJCElYSepFtSDQCN998syasdevWJbqt2RpHwsqGEO8TgQIjsGLFCvXNN9+ohQsXFrgmhS+ehFX4PmANiAAR8IgACcsjUIxGBIhA4REgYRW+D1gDIkAEPCJAwvIIFKMRASJQeARIWIXvA9aACPhG4Pfff1eTJk1SQ4YMUaNHj1affvqp7zzimICEFcdeY52LGoE777xTlS5dWps6iFFpw4YNE48LCSvxXcwGJgmB3r17b0VUQlgIq1atmqTmbtUWEtZWkPACEYgmAosXL85IVkJcXbt2jWYDLNSKhGUBRGZBBMJAAAdOCCllCkuVKqW2bNkSRpVCL4OEFTrkLJAI5IYAXCNnIirzHo60T6KQsJLYq2xTIhE45JBDPBPWypUrE4kBCSuR3cpGJRGBSy65xBNh4VSdpAoJK6k9y3YlDoElS5Z4IixOuieu69kgIhBPBPr375+RtHbaaad4NsxjrTnC8ggUoxGBqCDg9mp42GGHJXZ1ULAnYQkSDIlATBA44ogjUqOsbbfdVl1++eV6xHXeeefFpAW5V5OElTt2TEkEQkdg6dKlmqAOPfTQVPlVqlTR10KvUMgFkrBCBpzFEYEgCAwaNEiTEzY9Q84//3x9LeleSUlYQbSHaYlAyAjstttuKXLC6+CqVatSpb/66quasEBoSRYSVpJ7l21LFALz58/XxHTiiSeWaJtYuWPiPclCwkpy77JtiULg0ksv1YQ1ZcqUEm1r0KCBvlfiRsJ+kLAS1qFsTnIRkFFU2bJl1YYNG0o0tG/fvpqwXnvttRL3kvSDhGW5N6dOnarq1aunmjRpstWncePG6uqrr1YTJ060XCqzSzoC5jxVp06dtmouJtuF0Dp06LDV/aRcIGFZ7slu3bppxREFcgtnz55tuXRml1QETjnlFK1Xn3/+edpmip7ttddeae8n4SIJy3Iv1qpVK6VYlStXVv369VM33XSTuvHGG1Nhx44dVfXq1bXiQcFwQCaFCGRDQMioWrVqrlHbtm2rdWv58uWu8eJ8g4RlufdEsTJZHYPAJF7Lli0t14DZJQ2B8ePHa33BA9BNHn30UR1v6NChbtFifZ2EZbH7li1bphVGjPrcshfC2nvvvdWmTZvcovE6EVD169fXerVmzRpXRDARL3rVtGlT13hxvkHCsth748aN0wrz9ddfZ8y5UaNGqbiYb9i4cWPGuLxZvAjgOC8hIS82VrvvvnsqfpkyZdSff/6ZOOBIWBa7FKszolzZsq1UqVIqbo0aNbJF5f0iRgDzoKJTeCBmE6xCS/y5c+dmix67+yQsi122//77p5Ql25MQ/rZFqWAMSCECbghgkl10xS2OeX3mzJk6Pjw5JE1IWBZ7VBSrZ8+errmuW7dOKxTir1+/3jUubxQ3AgsWLNC6ArMGryJ6WLNmTa9JYhOPhGWpqz788EOtXDiZF8qGvV/4fPLJJ+rFF19UWDkUZUKY1KVnS5AWfTadO3fW+gLDUa9y1FFH6XQ//PCD12SxiEfCstRNt9xyi1YSk5Sc39u0aaO8zEVYqhaziSkCWIjZddddtU75acZ9992n0z388MN+kkY+LgnLUheZRnulS5dWOLkEn+23314rD8jr6KOPVl999ZWlUplNUhGYNm2a1psuXbr4aiaMkeVBedJJJ/lKG/XIJCxLPQTzBCjJ8ccfnzZHvDJif6EoUtKefGkbzYs5IwD3MaIrH330ke98sEEa6WHm4Nwo7TuzCCUgYVnojD/++EMr1+DBgzPmKP64oUxJtJPJ2Hje9ITA6tWrFRz0QUfwWpiLXHjhhVon33333VyyiGQaEpaFbjGXkrPZvsCPkTw5x44da6F0ZpE0BMaMGaN1ZMCAATk175VXXtF5YCtYUoSEZaEnr7vuOq0c2bJbsWKFjot0FCLgRMA8kh6HTuQiv/76qypVqlRK1w444IBcsohkGhKWhW6RuSkvh1jOmzdPExbMHyhEwETAnDCvU6eOecv399q1a2tdw4MyCULCCtiLmNCsWLFiSjHOPPPMrLn16NFDK9Fbb72VNT4jFBcCpufQBx98MFDjTVObpDiNJGEFUgmlzG022Tw0wFBU5q+wOZVCBJwIyOZlvM799ttvztu+fn/88cda38466yxfaaMamYQVsGcee+wxrRSZrIqHDRum44G03n777YAlM3nSEHjnnXe0jtiwn4LbItlkDwJMgpCwAvYi/GvLqAlzWTAMxdYI+ZjWyhJv+vTpAUtl8iQi0L59e61LM2bMsNLEVq1a6TxzseeyUgmLmZCwAoJZtWpVrRBCSG4hTuhdu3ZtwBKZPKkIiN5UqFBBbdmyxUozMXcl+Q4ZMsRKnoXMhIQVAP2///5b3XrrrQoTpf379y/xgStbzGlNmjRJLVq0KEApTFoMCDz33HOaWLp27WqtyaYZTdBVR2uVCpARCSsAeExKBGwhIB5oMRpyOxUn17JAVDLKyjWPqKQjYUWlJ1iPokXg33//1YSSDyNP0wvp5MmTY40zCSvW3cfKJwGBe++9VxMWbKdsywcffKDz9+v5wXZdguZHwgqKINMTgYAIVKlSRRMK7Ppsyz///KN23HHHVBk77LCD7exDzY+ElUe4V65cmTIszWMRzDrmCMA4VOaXGjdunLfWmCdHw7tIXIWElYeeg/N/UUIJL7roImtL1XmoMrMsEAJ9+vTRuoKDUPMl999/vy4H3+MqJCzLPSc75IWozBDDcgoRMBHAhnnREfO67e/w3iDl+DnQwnY9guZHwgqKoJG+efPmWilEOZwhjm2iEAEgAMtz0Y8zzjgj76D4PTIs7xXKoQASVg6gpUtizkWIErqF2JRKIQLmwbtheO6AQaroJFYO4ygkLEu9Zm6CFqVwC2+//XZLpTKbOCMg+gF3yGHI66+/rgkr09mZYdQl1zJIWLki50g3cuRIrQyiiG4hPY06wCvCny+88ILWl6uuuio0BEQn47pNh4RlSVXmzJmjFVCUwi0M6pjNUpWZTQERME/F+f7770OriXnIKvbCxk1IWBZ7bJdddvFEWps3b7ZYKrOKGwLmfCcc9oUpt912m9bRp556KsyirZRFwrIC438zqVGjhlYGt9EVrt9www0WS2VWcUNgxIgRWk9AIGEKRnOim2GsTNpuGwnLEqLHHXecVgRRiEzhlVdeaalkZhM3BA4++GCtK7///nvo1Re9hN+tuI32SVgW1OXss8/WCghlwJJxt27d1GGHHaYaNGigQE5LlixREyZMKBGvXbt2FkpnFnFCAL7RhDBAXIUQjKykDgsXLixEFXIuk4SVM3T/TYgtN9L5CLMdHPDSSy+ViA+XypTiQaBXr166//O5FScTok8++aSuw6BBgzJFjdw9ElaALsFytElWXld7PvzwwxLp8uEDKUCzmDSPCOyxxx667/NYTMas8Rooenv44YdnjBu1mySsHHukd+/eutPR+X4d/H/55Zcl0u+5554KbkAoyUXgjTfe0H3etm3bgjZ033331XX55ZdfCloXP4WTsPyg9b+4gwcP1p0Nspo6dWoOuSiF+YPttttO51WuXDmFTaqUcBAw99bJiENC+KjCVhac1G1LTj/9dN3XsDovpFx//fW6LnHyQkrC8qk1Y8aM0R0N5X766ad95lAy+rJly1T58uV1nnCwhmuU/CKA1TlgLQSVKaxfv75as2ZNoAr99ddfujw8mAot2LsobcaexrgICctHT5lHJqGzx44d6yO1e1T8GWrWrKkVCHnjlZGSPwTee+89jTde7zHiee2119SUKVMUTrC54IILlOkqCAaeQUwQYKQpBNG9e/f8NcxHzlIfvB7GRUhYHnvq3Xff1QqHjr755ps9pvQWDfNXeJKLEiHE5DwlPwgMHz5cY/3NN9+kLWTdunXKtK9r2LBh2nheLh555JG6vM8++8xLkrzHadq0qa7TV199lffybBRAwvKA4tdff607FkRyzTXXeEiVW5RjjjmmRFl44lPsI9CmTZsUzhg5bdiwIWMBBx54oO6Tt99+O2PcdDfNrTgYSUdFHnjgAd0ubN6Pg5CwsvQS5pPMUQ9Ob863NGvWrESZsJuh2EVgt912S2EMw95sMnv2bN0feFX0KjBzwUG6HTt21OmHDRvmNXne45lGrBgBxkFIWBl6CU9G+CoSwgKRhCWmNTLKj7Mf7rAw81oOTqaRPu3Ro0fWZPBqIAsjFStWzBp/8eLFCrZ1UoYZRs15Y+XKlVP1hPvu9evXZ21boSOQsFx6YOPGjcr0vnDooYe6xMzfZacVve15s/zVPNo5Y3JdSMSrSYp5MnOm1i1YsEDnLWU4QxBaVOSSSy7R9cVIMupCwnLpIXmiQtkKaYl+4403aoVCXS677DKXGvOyVwSwHUVIxKsJiTn5/ueff7oWhQ3FkrdbWL16ddf0Yd8wvZDGYUM+CSuNhlStWlUr3X777ZcmRriXxo0bp+uDPwE2W1NyRwD7N4EjlvO3bNniKSMvhDV9+vQS/eRGWLg+d+5cT+XmOxJMNeTkHpBt1IWE5eghvPqJou2zzz6Rcb9hutRF/eCxkpIbAtK/J598sucMTE+dbokGDhyodUfKcAtt2fC51cXPdXgVkXouXbrUT9LQ45KwDMiPPfZY3XFY7o7aHquZM2fq+kHBoGgUfwjgDyl/zrvuustTYsxnyt47zGu6iR/CwmG7UZG7775bY/LII49EpVpp60HC+h8s5j4vrJhE9Unj9PSw//77p+1YXkyPwLPPPqv/nF43rJsk16JFi/QZK6WmTZum8xZSzBTiVezMM89UsLovpJgLBVE/ZJWEpVRqk6upWOjAKAsss0uXLq3/HHvvvXdBl6QxD4Ql8Tgsi4tLIJireN1qc++992qsYWzpJps2bVJeJt1NXZPv6MNrr702tSHeLf98Xsf0h9Qln+UEzbvoCatfv366o9BhcdkO89NPP6mdd95Z1x2GkLAvKoScdtppKRMQjBjefPPNQlTBc5kYkaKfDznkEM9pzEWYVatWZUxnmkwIAThDzEfeeuutSmygnPdRNxiYhum545xzztG6ZNNDRUawcrhZ1IQFpTCVJYzTd3PoI9ck//77r8Jcm7QB3gfgijlMmTFjhi4f9SiUF02vbRasOnXq5CnJQw89pNvXqlUrT2lASNtvv71OJ2WC0J2rg3gdhPW8aaAs8RFiv98zzzzjqdwgkV588UVdX5jSRFWKlrBwNqCpGHHeswffTWZbvvjii9D0DWYfZtkYsUZVYLApdQURZZPVq1fr+Ej3ww8/ZEtS4j48NOA1D94gQGLZBKRhmk9IXSXEKChfox94DJFyomQn5sSsKAkL7kOkcxBGfVTg7LR0v+vVq1eiTWFM5D7xxBOpMjH/Ubdu3dT3s846K131InFt1KhRGqOVK1dmrBO245g7HbyuKGbM1ONNjJxHjx6t3I6Nw6IQXNTYXhgyzRs8VjVrtMaNG2vMzf9cuu9e3O4UHWE5V3LCPhcuaw8HiHDqqaeWUI5XXnklQG7Zk8rEP7xXwoMFlNDP3FD2EuzGwGsg6li2bNmMGYMszD+Ulz9SxgwD3MTCwIABA7TzP7Ne+I5JfsyHZbK+91o8zsuU/LGaakOw91LyzBZieiGbFBVhwTWICRpOMEmayJ9S2nnfffelmvjtt9+q8ePHqzvvvFPh5B6vFt5u+PTt21djiTj4U6NMuHyOqmAlDnU84YQTUlWEfRU+f/zxh5ozZ07qgFvnXFKUHmjwo9W5c2eNu/SxhLVr11ZB7KjgE0vyOu+88wJ3I9z2SH7YZI5RP3BO98FAwosUDWGZnQEQL730Ui/4xDIO5k1EURBi1GP+lu/33HNPTu0D2UkeYgA5dOhQfS2nTENIJHX2EuIV+7vvvguhVrkVgTnX5s2ba8ydbcJoGyuWfsV8Dfab1hnfXDG15aWiKAjrxx9/LNGxNp4ezs6J2u8hQ4aUaLNToeV3z549fVf94osv1nmvXbs2lf7555/X11asWOE7z3wnwFNd2pwuxAorHPVhc3lcvG8CM8y1YZsP/Hq5tQv95XVOEyYqkg8WHYKIedBFkHzMtIknLAz3zZNp0CHFIq1bt9bKJ0qYLvzkk088Q2J6zzTd3Xz66ae6rCjaYkEPMGKCdwbnB6t/uB93wYMCJGHajZn9jTMR8SqfyfTFXJCCGQcWVjCdkIuI91ysYtuSxBOWaVyJJeNiEkwumwrr9t2rTRKww9YUyQfzPyLmsniQeRTJj2EwBMS+y00H8MoLq33nflm4mJH+NUN42sXqpR8RLxAwx7AliSYs0z4JHVQsghUj89BOU/HSfa9Vq5YnaEw7JmxXMQVlyqohnuKUaCCAw01efvnllAFqur7HIgP2D2KFDlMl6eLINT//oeXLl+u8vNi8eUUrsYQldkEAO07HGHntOImHY8cx5wIXyniS1alTRyuKKFq28KCDDpLsMoZyqg9GrelE7IawoZcSPQQwmoJvNfNBnk03nPe92qPBOl/SBj3T0UQykYSFZWsBC0/9oEv4JmCF/o5RDpQOBxu4rf5J272GcMWcTWbNmqUxhd0P9i2iLvhgjgMLG0cccUQqTpRtsbK1s1juYwM95rvKlCmj+9WLvlSqVMkTRHiFlPy6dOmSMsfA1IP5gQ63b9/eU34SKXGE5Ty8IdsRTgJEFENMEmM4DULxM3Lac889FZTEaUgqCuQMvZyTt9dee2kFdKZ3/o6yLVYU+7nQdcLDSOabnH3p/I3DZb2MmPD66Eyb7jdeSf1IogjLaTQZ5m53P6Cni4uVG2wRwqEAmFNK17npruF1F08zbDv5/PPPt8o6XRrzGva5ZZOHH37Yc30k72x58n60EKhWrZqnPsbDSExZ3FoAN0Myn4kHHUbemE5wfmDo6td4OzGEBfsZ+bMgzHUp1q0TbF5fuHChevzxx1PGq+YhnWb9033HYRgdOnRIzVf5OcrefEU283VOnKdrI3w8iecBKDUEcyHOD+yBRowYofvAq6+pdGXyWvgIHH/88brvTB1xfgcBZRNsvpd0Tz/9dLbovu7nhbCgvHDnixEDlrgnTJiQMsfPl63LddddpwECUDhWPiqCU6MxAdmtWzdfr3UYZZ177rm+ycmt3Xi9BEENHjxYTZw40S3aVtcxAhPly+YrzNz6lC+vAltVkBesIOB0EyR97gwxks8m5oMLc5w2xSphodHm+W3OxuI3HKiBzGzJ7bffrv9QyN/rOXO2yjfzwUQmXITAehyHWeB9Px0GzmsYGmNlDR2N+SSMaqIgsHSWvXXo12xiLmUnwQNGtvYm7T4mwJ26af5u2LChpyab1vKeEviIZIWwYEBonioijcRObRCUecYf7g0fPtxHFd2jwvBNykJoe/jpVjJWHfHkwH4ujO7wju5moGfWDwRWs2ZN1aZNmxQ5wTo823yAWx3CuG6u9Hjxf27uMYyyE7gwsItrGf379y/xnxL9xdyq19V2OfUac1a2JTBhYXm7XLlyupHwjQSvANgmIC4vMAmH7Q9Yjscf1obAdYqAiTBfR7nDzgl1x6iwT58+qRGkm2tbsz5YLsacD7bH4FQSvE4F3ZtlAzeveWCOTNrTtm1br8kUXDUjnU3rZs+FM6IVBDA/iWkM2FxhrtWP40L4GRO9gbsa2xKIsLAKZ+7uhpeAMOT999/XoACcW265xUqxeIKgs3BkN540mKyW452kE9KFGDlhnxa2rcBrAebQ4HM9zoJzD6WtixYt8twUOdeRR5B5hixREc1N5pMnT7betkCE1aRJE63UXi1gg7bAfPLjD4XJ7FwFiwOYKAbhNWvWLDUikj9pphAjSrj2QJvRQdm8V+Zav0KlM41EYSriR2T+ItP5fX7yY9x4IQCjYvnv5OONImfCwqSqVAxn+tmWdevWqZEjR6orrrhCwU84PApg1CJlIvRrJYuVK0zS4zXNbUe7mT++49UOZHbHHXco/JHz0Qm2sQuaHwgYCwgwv/A6byFlYtSNEZnt1SHJn2G0EcDEPP43cNeD/wp0AXrk/GDgkYudZM6EZc7j2IYQc0VO4nD+ht1IJpk/f35q7qhdu3bKPHPNmY/5G0ZxICd4mcSKJ0iTQgSIgDcE8HAzecH8b6X7nsuKfk6EhRNApALwN21TxNWu5J8uPPnkk0sUiQltrDziAATsdUqXxnkNxpAgJ7wOYuSEyXUKESACuSMAkxzn/yzT72xnPKarSU6EZXo3tOld0rSQzdRQTG5jf515Jl+m+IiHNIMGDUq5XUkHBK8RASIQDAHs24XVAPYaZvrgVRCOIHMR34SFgvB+CoKAwaNNAQllIh4v97Bah02/GPnZNFC12U7mRQSIQG4I+CYsc/sF5ppsikzYeSEmxIHJAZyPYVIer3Vi92WzTsyLCBCB6CDgm7Dg8F4IBdtQbEq2bT1SLkIvLlFs1o15EQEiUHgEfBOWaboPA06bgj14Jill+m6zXOZFBIhAPBDwTVjmPJPtUY7zOC43wsKhjBQiQASKDwHfhIUDSIVIsHnXtuCkYsk/XXjwwQfbLpL5EQEiEBMEfBOW6esGZ5jlQ+A/Kx1Z+dmEm496MU8iQAQKi4BvwoKpgJCJHFOerybA2hyeH+BwLhcjs3zVi/kSASJQGAR8ExYMwsSpG4gL555RiAARIAJhIOCbsFAp03863IlQiAARIAJhIJATYcHDKLyJyqthhQoVUqfL/vXXX7rOcNoHswfs1cNmYgoRIAJEICgCOREWCsWcUrq9fDjeR05ZEUKDOxcKESACRCAoAjkTFgrGZkc40DNdJAtJSQg3wXCNTCECRIAIBEUgEGFJ4XgVxDmAWM2D65lJkyYp2GjZ9OQgZTEkAkSgeBGwQljFCx9bTgSIQJgIkLDCRJtlEQEiEAgBElYg+JiYCBCBMBEgYYWJNssiAkQgEAIkrEDwMTERIAJhIkDCChNtlkUEiEAgBEhYgeBjYiJABMJEgIQVJtosiwgQgUAIkLACwcfERIAIhIkACStMtFkWESACgRAgYQWCj4mJABEIEwESVphosywiQAQCIUDCCgQfExMBIhAmAiSsMNFmWUSACARCgIQVCD4mJgJEIEwE/gMpnzaigG2hFQAAAABJRU5ErkJggg==[/img][br][br]Select [b]all[/b] true statements after the transformations:
This design began from the construction of a regular hexagon.
Is quadrilateral [math]JKLO[/math] congruent to the other 2 quadrilaterals? Explain how you know.