İki Paralel Doğru Arasında Neler Oluyor?'in kopyası

Bu etkinlik, MAT.6.3.2 numaralı "Matematiksel araç ve teknolojiden yararlanarak iki paralel doğrunun iki kesenle oluşturduğu şekillerin özelliklerine dair çıkarım yapabilme" öğrenme çıktısına yönelik hazırlanmıştır.[br]a) Düzlemde iki paralel doğrunun iki kesenle oluşturduğu şekillerin özelliklerine dair varsayımda bulunur.[br]b) Oluşan şekilleri çeşitli özelliklerine göre listeler.[br]c) Oluşan şekilleri kenar ve açı özelliklerini dikkate alarak varsayımları ile karşılaştırır.[br]ç) Oluşan şekillerin iç açılarının ölçüleri toplamına ve yamuk, paralelkenar, eşkenar dörtgen, dikdörtgen, karenin ortak özelliklerine dair önermeler sunar.[br]d) Sunduğu önermelerin dörtgenlerin sınıflandırılmasına yönelik katkısını değerlendirir. [br]

Dörtgen Dönüşüm İstasyonu

Sıradan bir Paralelkenar, doğru komutları aldığında başka şekillere dönüşebilir mi?Aşağıdaki [b]kumanda panelini[/b] kullanarak şekle talimatlar verin. Açıları dikleştirin veya kenarları eşitleyin.[br]Bakalım [b]Dikdörtgen, Eşkenar Dörtgen ve Kare[/b] aslında birbirinin akrabası mıymış?[br][br][b]Görev:[/b] Düğmelere basın ve değişimi izleyin! (iyi eğlenceler :))

Dikdörtgen Deneyi: Sürgülerle oynayarak rastgele bir paralelkenar yapın. Sonra "Dikdörtgen Yap" düğmesine basın.

Şekil dikdörtgen olduğunda kenar uzunlukları değişti mi,yoksa sadece açı mı değişti?[br]Buna göre; "Her dikdörtgen aynı zamanda bir paralelkenardır" diyebilir miyiz?

Eşkenar Dörtgen Deneyi: "Eşkenar Dörtgen Yap" düğmesine basın.

Kenarlar eşitlendiğinde açılar 90 derece olmak zorunda mı?[br]Şekli tekrar bozun ve açıyı (ac) değiştirip tekrar düğmeye basın. Açılar farklıyken de eşkenar dörtgen olabiliyor mu?

Kare Deneyi (Büyük Final): "Kare Yap" düğmesine basın.

[*]Bu düğme şeklin hem kenarlarını eşitledi hem de açılarını dik yaptı.[/*][*]O halde kare için [b]"Kenarları eşit olan özel bir dikdörtgendir"[/b] tanımı doğru olur mu?[/*]

Soru 1: Dikdörtgenin Sırrı

"Dönüşüm İstasyonu"nda bir Paralelkenarı [b]Dikdörtgen[/b] yapmak için hangi özelliği değiştirmek zorunda kaldık?

Karşılıklı kenarları paralellikten çıkardık. Köşegenleri dik kestirdik. Kenar uzunluklarını eşitledik. İç açıların hepsini 90 derece yaptık.

Soru 2: Eşkenar Dörtgen ve Kare

Uygulamada [b]"Eşkenar Dörtgen Yap"[/b] butonuna bastığımızda kenarlar eşitlendi.[br]Eğer bu şeklin açılarını da [b]90 derece[/b] yaparsak ("Kare Yap" butonu), elde ettiğimiz [b]Kare[/b] için aşağıdakilerden hangisi söylenebilir?

Kare, hem özel bir dikdörtgen hem de özel bir eşkenar dörtgendir. Kare, sadece bir eşkenar dörtgendir. Kare ile eşkenar dörtgenin hiçbir alakası yoktur. Kare, sadece bir dikdörtgendir.

Soru 3: Ortak Özellik

Bu etkinlikte incelediğimiz Paralelkenar, Dikdörtgen, Eşkenar Dörtgen ve Kare şekillerinin hepsinin [b]DEĞİŞMEYEN ORTAK ÖZELLİĞİ[/b] aşağıdakilerden hangisidir?

Hepsinde karşılıklı kenar çiftleri birbirine paraleldir. Hepsinde bütün açılar 90 derecedir. Hepsinde bütün kenar uzunlukları eşittir. Hepsinde köşegen uzunlukları eşittir.

Biraz da elimiz çalışsın..

3 madde de 1.applet çıkarımı:

[list=1][*][b]Dikdörtgen:[/b] Paralelkenarın sadece açıları 90 derece yapılırsa [b]Dikdörtgen[/b]'e dönüşür.[/*][*][b]Eşkenar Dörtgen:[/b] Paralelkenarın sadece kenar uzunlukları eşitlenirse [b]Eşkenar Dörtgen[/b]'e dönüşür.[/*][*][b]Kare:[/b] Bir şeklin [b]Kare[/b] olabilmesi için [b]hem[/b] açılarının dik olması [b]hem de[/b] kenarlarının eşit olması gerekir.[/*][/list]

[size=200]ŞEKİL AVCISI[/size]

MERHABA! HAZIR MISIN?

Elimizde sonsuza giden iki tren rayı (paralel doğrular) olduğunu hayal et. Bu rayların üzerine rastgele iki çubuk (kesen) daha atarsak arada kalan kapalı bölge hangi şekillere benzer?[br]Bu etkinlikte şunları keşfedeceğiz:[br][list][*]Paralel doğrular arasında oluşan şekiller nelerdir?[/*][*]Bu şekillerin özellikleri (kenar, açı) nasıl değişir?[/*][*]Yamuk, Paralelkenar ve diğerleri aslında akraba mı?[/*][/list]

APPLET 2 İN AÇIKLAMASI

Birinci appletimizde A,B,C,D noktalarımızı haraket ettirerek ABCD dörtgenleri oluşturmaya çalışıyoruz.[br]Applet dörtgenden farklı bir şekil çıktığı zaman dörtgen oluşturmayacak şekilde tasarlanmıştır.[br]NOT:Noktaları haraket ettirerek ABCD dörtgenleri oluşturmaya çalışın.

Biraz Dörtgen Avlayalım

"Noktaları hareket ettirerek bu düzenekte gizlenmiş özel ABCD dörtgenleri avlayabilir misin? Aşağıdakilerden hangilerini elde edebildiğini not et:"[br][list][*]Yamuk[/*][*]Paralelkenar[/*][*]Dikdörtgen[/*][*]İkizkenar Yamuk[/*][*]Kare[/*][*](Elde edemediğin var mı? Neden?)[/*][/list]

Açılar Arasındaki Gizli İlişki

Şekil üzerindeki [b]A açısı (sol üst)[/b] ile [b]D açısını (sol alt)[/b] toplayın. Sonra noktaları hareket ettirip tekrar toplayın.[br][list][*]Bu iki açının toplamı her zaman kaç derece çıkıyor?[/*][*]Aynı durum sağ taraftaki (B ve C) açılar için de geçerli mi?[/*][*]Bu özellik sadece bu şekle mi hastır, yoksa paralel raylar arasındaki her dörtgen için geçerli midir?[/*][/list]

Özel Yamukları Bul

[list=1][*][b]İkizkenar Yamuk:[/b] Sol ve sağ kenar uzunluklarını birbirine eşitlemeye çalışın. Bu durumda taban açıları hakkında ne fark ettiniz?[/*][*][b]Dik Yamuk:[/b] Kenarlardan birini raylara tam dik (90 derece) yapın.[/*][*][b]Dikdörtgen:[/b] İki kenarı da aynı anda dik yapabilir misiniz? Yaparsanız bu şekil hala bir yamuk sayılır mı?[/*][/list]

Yamuk Nedir?

Yaptığınız gözlemlere dayanarak "Yamuk" şeklini bir arkadaşınıza nasıl tarif edersiniz?[br](İpucu: Paralel olan ve olmayan kenarlardan bahsederek bir tanım cümlesi yazınız.)

Soru 1: Değişmeyen Özellik

"Şekil Avcısı" uygulamasında noktaları sağa-sola hareket ettirdiğimizde dörtgenin şekli sürekli değişiyor. Ancak bir özellik [b]ASLA[/b] değişmiyor. Bu özellik hangisidir?

Alt ve üst kenarın birbirine daima paralel olması. Köşegenlerin birbirini ortalaması. Tüm açıların 90 derece olması. Tüm kenar uzunluklarının eşit olması.

Soru 2: Açıların Gizemi (U Kuralı)

Şekil üzerindeki [b]Sol Üst Açı[/b] ile [b]Sol Alt Açıyı[/b] topladığınızda sonuç kaç derece çıkıyor? (İpucu: Noktaları hareket ettirip tekrar deneyin).

Her zaman 90 derecedir. Her zaman 360 derecedir. Her zaman 180 derecedir. Toplamları sürekli değişir, sabit değildir.

Soru 3: Dönüşüm

Bu yamuk şeklinde, yan kenarları (kesenleri) da göz kararı birbirine [b]paralel[/b] yapmaya çalışırsanız şekil hangi dörtgene dönüşmeye başlar?

Paralelkenar Daire Üçgen Beşgen

Applet 2 için 3 madde çıkarım:

[b]Yamuk Kuralı:[/b] Alt ve üst kenar hep paralel raylar üzerinde olduğu için şekil daima bir [b]Yamuktur[/b].[br][b]Açı Kuralı:[/b] Paralel kollar arasındaki alt ve üst açının toplamı değişmez, hep [b]180 derece[/b] dir.[br][b]Çeşitlilik:[/b] Yan kenarlar bağımsız hareket edebilir; şekil [b]Dik[/b] veya [b]İkizkenar Yamuk[/b] olabilir ama paralellik bozulmaz.

DÖRTGENLER HİYERARŞİSİ

Sadi karayele ait 2015 yılında yayınlanmış güzel bir applet.Appletin boyutlarını bu çalışma sayfama göre ayarlayıp kullanmak istedim.Bence bu appletin amacı bir dörtgenin kenar uzunlukları ve açılarını değiştirerek, şeklin hangi koşullarda kare, dikdörtgen, paralelkenar veya eşkenar dörtgen haline geldiğini keşfetmeyi sağlamak.

Soru 1

Applet üzerindeki sürgüleri kullanarak bir [b]eşkenar dörtgen[/b] oluşturunuz.[br][br]Eşkenar dörtgeni oluştururken [b]hangi özellikleri sağladınız?[/b][br][br]Bu özelliklerin neden eşkenar dörtgen için zorunlu olduğunu açıklayınız.[br]

Soru 2:

Kenar uzunluklarını ve açıları değiştirerek şekli önce [b]dikdörtgen[/b], ardından [b]kare[/b] olacak şekilde ayarlayınız.[br][br]Bu iki dörtgen türünün [b]benzer ve farklı[/b] özelliklerini, applette gözlemlediğiniz ölçüler üzerinden açıklayınız.[br]

Test Sorusu 1

Applet üzerinde bir dörtgenin [b]bütün kenar uzunlukları eşit[/b], ancak [b]açıları 90° değil[/b] olarak ayarlanmıştır.[br]Bu durumda oluşan dörtgen türü aşağıdakilerden hangisidir?

Eşkenar dörtgen Paralelkenar Kare Dikdörtgen

Test Sorusu 2

Applet üzerinde bir dörtgenin [b]karşılıklı kenarları eşit uzunlukta[/b] ve [b]bütün açıları 90°[/b] olacak şekilde ayarlanmıştır.[br]Bu dörtgen aşağıdakilerden hangisidir?

Yamuk Paralkenar Dikdörtgen Eşkenar dörtgen

GÜNDELİK HAYATTA MATEMATİK

Paralel doğrular nerede karşımıza çıkacak ya hocam?

Mesela etrafımızdaki bir merdiveni dikkatlice incelediğimizde basamakların arasında birer dörtgen oluştuğunu gözlemleriz.

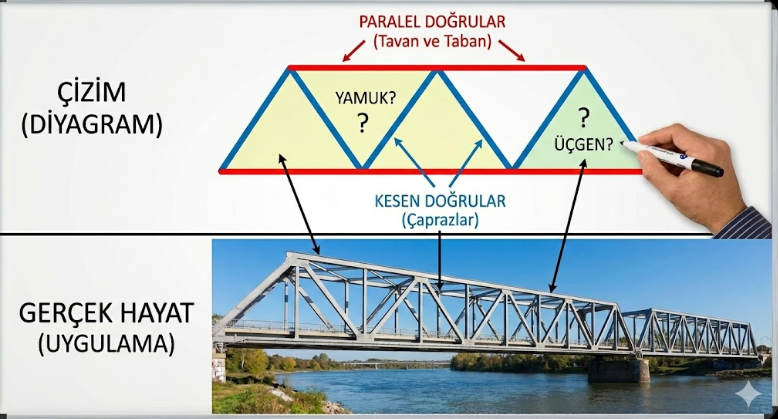
Appletler yardımıyla konuyu keşfederek öğrendik şimdi bu konuyu özetleyecek bir viedo ile konuyu pekiştirelim..

Konuyu genel hatlarıyla ele alan bir anlatım:

Short viedosu mantığında kendimizinde yapabileceğini eğlenceli bir etkinlik:

Dörtgenler ile ilgili bir siteden konu anlatımı yapmak için aşağıdaki linke tıklayabilirsiniz.

Bu çalışmamızı tekrar ettirecek nitelikte olan bir dosya bırakıyorum bu görseli çıkartıp dolabınıza asabilirsiniz.

PROJE SONUÇ RAPORU VE DEĞERLENDİRME

[b]Giriş ve Amaç:[/b][br]Bu proje, [b]MAT.6.3.2[/b] öğrenme çıktısı kapsamında; matematiksel araç ve teknolojilerden (GeoGebra) yararlanarak, iki paralel doğru ve bunları kesen doğrular arasındaki geometrik ilişkileri analiz etmek amacıyla hazırlanmıştır. Çalışma boyunca statik tanımlar yerine, şekillerin birbirine dönüşüm süreçleri (dinamik geometri) incelenmiştir.[br]