GeoGebra eigenständig nutzen
Workshop im Rahmen der GeoGebra-Tagung 2021
Table of Contents
- GeoGebra Classroom kennenlernen
- Kurzübersicht GeoGebra Classroom
- Aktivitäten erstellen und finden
- Einheit erstellen
- Schüler*innenarbeit beobachten
- GeoGebra App Aufgaben
- Namen verbergen
- Ideen im Lehrplan
- GeoGebra Ideen im Lehrplan - GGB-T21-C4
- Konstruktionen
- Konstruktionsbeschreibung - GGB-T21-C4
- Inkreis eines Dreiecks-GGB-T21-C4
- Konstruktionsprotokoll Inkreis GGB-T21-C4
- Weitere Anleitungen
- Schnitt von Funktionen
- Gleichungssysteme lösen
- Ableitungen bestimmen
- Bestimmtes und unbestimmtes Integral
- Binomialverteilung
- Eigene Anleitungen entwickeln
- Rhombus
- Raute konstruieren
- LGS grafisch lösen
- Fundstücke digital umsetzen
- Prüfungen
- Übersicht Prüfungsmodus
- Android
- iOS
- Windows & MacOS
- Tipps
- Jetzt kommt die Prüfung
Kurzübersicht GeoGebra Classroom
Auf den folgenden Seiten sehen Sie eine Auswahl an Infos (Aktivitäten) aus dem Tutorial "Lerne GeoGebra Classroom" des GeoGebra Team Germany.[br]Das komplette Tutorial ist erreichbar unter:
GeoGebra Ideen im Lehrplan - GGB-T21-C4
Gehen Sie den Lehrplan Sek I mit den Handreichungen für einen Doppeljahrgang [br]bzw. den Lehrplan Sek II durch[br]und suchen Sie nach konkreten Empfehlungen für den GeoGebra-Einsatz (CAS, dyn. Geometrie,…)[br][br]Tragen Sie die Ideen stichpunktartig (mit Seitenangabe) nach Leitideen geordnet in das jeweilige Conceptboard unten.[br][br][i]Tipps:[br]Funktion <Ctrl> + <F> im Dokument nutzen und nach den Schlagworten [br]Computer, CAS, digital, GTR, Software, dynamisch, Geometriesoftware, … [br]suchen.[/i]
Material: Lehrpläne Mathematik
Mathematik_RahmenLP_SekI
Mathematik_Anregungen_5-6
Mathematik_Anregungen_7-8
Mathematik_Anregungen_9-10
Mathematik_LPErgaenzung_SekII
Konstruktionsbeschreibung - GGB-T21-C4
Es soll zu einem gegebenen Dreieck der Inkreis konstruiert werden.[br]Notieren Sie eine Befehlsfolge für GeoGebra mithilfe der folgende Befehle:[br][br] Schneide(Gerade, Gerade)[br][br] Winkelhalbierende(Punkt, Punkt, Punkt)[br][br] Strecke(Punkt, Punkt)[br][br] Senkrechte(Punkt, Gerade)[br][br] Kreis(D, Strecke)
Erproben Sie Ihre Konstruktionsreihenfolge nun in GeoGebra.
Notieren Sie jetzt auf Basis Ihrer Befehlsfolge stichpunktartig eine Konstruktionsbeschreibung.
Schnitt von Funktionen
Aufgabe
Erstelle eine lineare Funktion mit Schiebereglern und schneide diese mit einer quadratischen Funktion.[br][br]Erforsche die Konstruktion und lerne, wie du eine Funktion mit Parametern erstellst und wie du mit dem [i]Grafikrechner [/i]in der [i][url=https://www.geogebra.org/calculator]GeoGebra Rechner Suite[/url] [/i]zwei Funktionen schneiden kannst. Danach versuche es selbst, indem du die folgenden Anleitungen befolgst.
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1.[/td][td][/td][td]Gib die lineare Funktion [math]f(x)=a\cdot x+b[/math] in das [i]Eingabefeld[/i] ein. Es werden automatisch Schieberegler für die Variablen [i]a[/i] und [i]b[/i] erstellt.[/td][/tr][tr][td]2.[/td][td][/td][td]Aktiviere den [i]Sichtbarkeits-Button [/i]neben den Schiebereglern, um diese in der [i]Grafikansicht[/i] anzuzeigen.[br][/td][/tr][tr][td]3.[/td][td][/td][td]Ändere die Werte der Schieberegler für [i]a[/i] und [i]b[/i] und erforsche, wie sich der Graph von[i] f(x)[/i] ändert.[br][/td][/tr][tr][td]4.[/td][td][/td][td]Erstelle eine quadratische Funktion, indem du [math]g\left(x\right)=x^2[/math] in das [i]Eingabefeld[/i] eingibst.[/td][/tr][tr][td]5.[/td][td][/td][td]Verwende den Befehl [math]Schnittpunkt\left(f,g\right)[/math], um die Schnittpunkte von [i]f(x)[/i] und [i]g(x)[/i] zu erstellen. Die Schnittpunkte [i]A[/i] und [i]B[/i] werden in der [i]Grafik-Ansicht [/i]angezeigt, während die Koordinaten der Punkte in der [i]Algebra-Ansicht[/i] angezeigt werden[i].[/i][br][/td][/tr][tr][td][/td][td][icon]/images/ggb/toolbar/mode_intersect.png[/icon][/td][td][b]Anmerkung:[/b] Du kannst auch das [i]Schneide [/i]Werkzeug aus der [i]Werkzeug-Ansicht [/i]verwenden und die Funktionen auswählen, um die Schnittpunkte zu erstellen. [/td][/tr][tr][td]6.[/td][td][/td][td]Bewege die Schieberegler für[i] a [/i]und [i]b[/i] und beobachte, wie sich die Schnittpunkte [i]A[/i] und [i]B [/i]deinen Änderungen anpassen.[br][/td][/tr][tr][td]7.[/td][td][img width=24,height=24]https://lh5.googleusercontent.com/EeYLvel9HmsnYD7ZRVm-HBQtblHhlB35cdQzXdG11nyuG3R7BCgnyC_l3L8aKn1R4wNkQnlMJHA72jcGN8n5f2RRahLZMiuy01yMfDJFEssc0gxkkfajbgHSyt1KTilGP0RyH5NA[/img][/td][td]Wähle den Graph von [i]f(x) [/i]und [i]g(x)[/i] aus und ändere die Farbe der Funktionsgraphen mit Hilfe der [i]Gestaltungsleiste[/i], um die Konstruktion zu verbessern.[br][/td][/tr][/table]
Versuche es selbst...
Rhombus
Aufgabe
Konstruiere einen Rhombus und erforsche seine Eigenschaften.[br][br]Erforsche die folgende Konstruktion und finde heraus, wie du diese mit [i]Geometrie[/i] in der [i][url=https://www.geogebra.org/calculator]GeoGebra Rechner Suite[/url] [/i]erzeugst. Danach versuche es selbst, indem du die folgenden Anleitungen befolgst.
Erforsche die Konstruktion...
Anleitungen
[b]Anmerkung:[/b] Falls du die Mobile-App verwendest, gehe sicher, dass die [i]Objektname anzeigen [/i]Option auf [i]Nur neue Punkte[/i] eingestellt ist. Du kannst dies in den [i]Einstellungen [/i]des App-Menüs unter [i]Allgemein[/i] einstellen. [br][br][table][tr id=segment][td]1.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_segment.png[/icon][/td][td]Wähle das [i]Strecke [/i]Werkzeug aus und erzeuge eine Strecke, indem du zweimal in die [i]Grafik-Ansicht [/i]klickst.[/td][/tr][tr id=ray][td]2.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_join.png[/icon][/td][td]Aktiviere das [i]Gerade [/i]Werkzeug und wähle den Punkt [i]B [/i]der Strecke aus. Klicke anschließend für den zweiten Punkt in die [i]Grafik-Ansicht.[/i][/td][/tr][tr id=circle][td]3.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_circle2.png[/icon][/td][td]Wähle das [i]Kreis mit Mittelpunkt durch Punkt [/i]Werkzeug aus und erzeuge einen Kreis mit Mittelpunkt [i]B [/i]durch den Punkt [i]A.[/i][/td][/tr][tr id=intersect][td]4.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_intersect.png[/icon][/td][td]Aktiviere das [i]Schnittpunkt[/i] Werkzeug und erzeuge den Schnittpunkt von der Gerade und dem Kreis.[/td][/tr][/table]
Versuche es selbst...
Anleitungen (fortgesetzt)
[table][tr id=parallel][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_parallel.png[/icon][/td][td]Wähle das [i]Parallele Gerade [/i]Werkzeug aus und erstelle eine parallele Gerade zu der bereits vorhandenen Gerade durch den Punkt [i]A.[/i][/td][/tr][tr id=paral][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_parallel.png[/icon][/td][td]Erstelle eine parallele Gerade zu der Strecke durch den Schnittpunkt.[/td][/tr][tr id=int][td]7.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_intersect.png[/icon][/td][td]Schneide die beiden zuletzt erstellten Geraden, um den vierten Eckpunkt zu erhalten.[/td][/tr][tr id=rhombus][td]8.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_polygon.png[/icon][/td][td]Aktiviere das [i]Vieleck [/i]Werkzeug und erzeuge einen Rhombus, indem du alle Punkte entgegen dem Uhrzeigersinn auswählst.[/td][/tr][tr id=checkHide][td]9.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_showhideobject.png[/icon][/td][td]Blende alle Hilfsgeraden und den Kreis aus.[br][/td][/tr][/table]
Übersicht Prüfungsmodus
Wir glauben, dass Schüler*innen davon profitieren, wenn sie im Unterricht, bei Hausaufgaben oder auch bei Tests genau dieselbe [i]GeoGebra App[/i] verwenden. Dadurch haben sie die Möglichkeit, möglichst viel mit der App zu arbeiten und können unsere Technologie in allen Situationen optimal nutzen. Aus diesem Grund haben wir unseren[i] GeoGebra Prüfungsmodus[/i] erstellt und ihn in jede unserer Apps (z.B.: [i]Rechner Suite[/i], [i]CAS[/i], [i]Grafikrechner[/i]) integriert. Der [i]Prüfungsmodus [/i]sperrt mobile Geräte so, dass Schüler*innen während eines Tests nicht kommunizieren oder andere Anwendungen als [i]GeoGebra [/i]verwenden können. Wenn Schüler*innen an Computern arbeiten, wird eine visuelle Warnung angezeigt, sobald sie das Vollbildschirm-[i]Prüfungsmodus[/i]-Fenster verlassen. Diese Anwendung wurde bereits von mehreren Bildungsministerien in verschiedenen Regionen in der Praxis erprobt und genehmigt.[br][br]Die folgende Tabelle gibt einen Überblick darüber, in welchen Anwendungen der [i]Prüfungsmodus [/i]auf welchen Plattformen verfügbar ist.
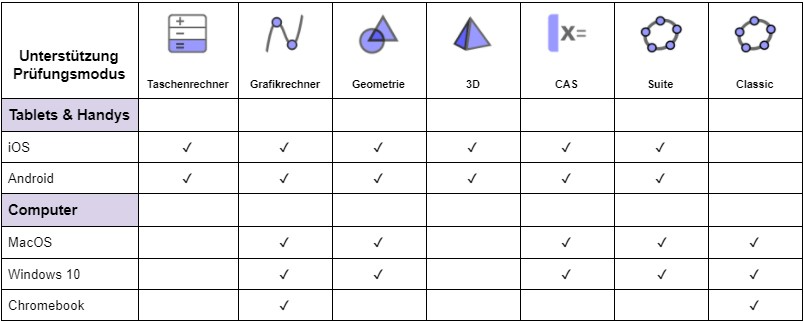
Vergleich von GeoGebra Mathe Apps
Wenn du jetzt noch herausfinden möchtest, welche App die richtige für dich ist und ob sie auch die Prüfungsvorschriften erfüllt, dann wirf einen Blick auf unsere Übersicht über die verschiedenen[i] [url=https://www.geogebra.org/m/vwh7kv4s]GeoGebra Mathe Apps[/url][/i].