Cette activité fait également partie d'un ou de plusieurs autres Livrets. Les modifications seront visibles dans tous ces Livrets. Voulez-vous modifier l'activité d'origine ou au contraire créer votre propre copie pour ce Livret ?
Cette activité a été créée par '{$1}'. Voulez-vous modifier l'activité d'origine, ou, au contraire créer votre propre copie ?
Cette activité a été créée par '{$1}' et vous n'avez pas l'autorisation de la modifier. Voulez-vous en créer une copie et l'ajouter au Livret ?
Buku digital ini dirancang untuk membantu siswa memahami konsep luas permukaan bangun ruang sisi datar secara menyeluruh dan interaktif. Materi difokuskan pada empat jenis bangun ruang utama, yaitu kubus, balok, prisma, dan limas, yang seluruh sisinya berbentuk bangun datar.
Di dalam buku ini, siswa akan diajak untuk:
1. Mengenal bagian-bagian penyusun bangun ruang sisi datar, seperti sisi, rusuk, dan titik sudut.
2. Memahami konsep dasar luas permukaan sebagai jumlah luas seluruh sisi pembentuk bangun.
3. Mempelajari rumus luas permukaan masing-masing bangun disertai penurunan rumus secara logis.
4. Menyelesaikan soal-soal interaktif yang didukung oleh visualisasi 3D melalui GeoGebra untuk memperjelas pemahaman.
5. Menerapkan pemahaman dalam kehidupan nyata, misalnya menghitung luas permukaan kotak hadiah, atap limas, atau wadah berbentuk prisma.
Pendekatan visual dan eksploratif dalam buku ini bertujuan untuk menumbuhkan pola pikir geometris dan keterampilan pemecahan masalah siswa. Buku ini sangat sesuai digunakan sebagai bahan ajar mandiri, penugasan proyek, maupun sumber belajar tambahan di kelas untuk siswa SD dan SMP.
Pada bab ini, siswa akan diajak mengenal lebih dekat bentuk dan sifat-sifat kubus sebagai salah satu bangun ruang sisi datar. Kubus memiliki 6 sisi berbentuk persegi yang sama besar, 12 rusuk yang sama panjang, dan 8 titik sudut. Pemahaman tentang bentuk dan bagian-bagian kubus ini menjadi dasar penting sebelum mempelajari bagaimana menghitung luas permukaannya. Dengan mengenali struktur kubus secara menyeluruh, siswa akan lebih mudah memahami konsep luas permukaan dan penerapannya dalam kehidupan sehari-hari.
[justify]Apa itu Luas Permukaan Kubus?[br][br][b]Luas permukaan kubus[/b] adalah ukuran seluruh area yang menutupi bagian luar dari sebuah kubus. Bayangkan sebuah kubus seperti kotak kardus yang tertutup rapat dari semua sisi. Kubus memiliki enam sisi yang semuanya berbentuk persegi dan berukuran sama. Nah, luas permukaan kubus adalah jumlah seluruh luas dari keenam sisi tersebut. Ini menggambarkan seberapa besar bidang yang dibutuhkan untuk membungkus kubus itu secara keseluruhan, seperti jika kamu ingin membalutnya dengan kertas kado.[br][/justify]Perhatikan dan amati animasi dibawah ini!
[justify]Animasi interaktif ini memvisualisasikan konsep luas permukaan kubus melalui transformasi jaring-jaring. Jaring-jaring kubus, yang terdiri dari enam persegi identik, diperagakan saat dilipat untuk membentuk bangun ruang kubus. Setiap persegi pada jaring-jaring merepresentasikan satu sisi kubus. Dengan demikian, luas permukaan kubus adalah total luas keenam persegi tersebut. Jika panjang rusuk kubus adalah [math]s[/math], maka luas setiap sisi adalah [math]s^2[/math], dan luas permukaan total kubus adalah [math]6×s^2[/math]. Dengan demikian, animasi ini secara efektif memvisualisasikan dekomposisi luas permukaan kubus menjadi enam persegi yang sama luas pada jaring-jaringnya, dan sebaliknya, bagaimana enam persegi tersebut membentuk luas total permukaan kubus ketika dilipat menjadi bangun ruang. Anda dapat melihat bagaimana setiap bagian dari jaring-jaring berkontribusi pada luas keseluruhan kubus.[br][/justify]
Kubus, meskipun terlihat sederhana, ternyata dapat ditemukan di banyak tempat dalam kehidupan sehari-hari kita. Bentuknya yang seragam dan simetris menjadikannya bentuk yang praktis untuk berbagai keperluan. [br]Dalam materi ini, kita akan mengidentifikasi beberapa contoh nyata kubus yang sering kita temui:
(a) Dadu
[justify][size=100]Salah satu contoh yang paling mudah dikenali adalah [b]dadu[/b]. Dadu yang digunakan dalam berbagai permainan memiliki bentuk kubus dengan sisi-sisi yang rata dan ukuran yang sama. Setiap sisi dadu biasanya dilengkapi dengan titik-titik yang mewakili angka, dan kita sering menemui benda ini di rumah atau tempat bermain.[/size][/justify]
(b) Rubik
[justify][size=100]Tak kalah pentingnya, [b]Rubik[/b] yang sering digunakan oleh anak-anak juga sering memiliki bentuk kubus. Rubik ini, yang dapat disusun dalam berbagai pola, biasanya digunakan untuk mengasah kreativitas dan kemampuan motorik halus anak-anak.[br][br][br]Melalui berbagai contoh tersebut, kita dapat lebih mudah memahami bagaimana kubus hadir dalam berbagai aspek kehidupan kita, meskipun sering kali kita tidak menyadari keberadaannya.[/size][size=100][/size][/justify]
5.2 Sifat-sifat Kubus
[*][/*][justify]Kubus memiliki beberapa sifat penting yang perlu diketahui, antara lain:[/justify]
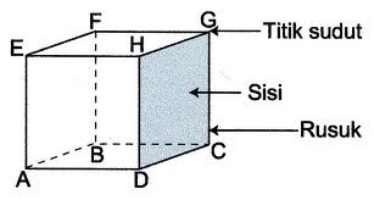
[list=1][*][b]Jumlah sisi:[/b] Kubus memiliki 6 sisi yang semuanya berbentuk persegi.[/*][*][b]Panjang rusuk:[/b] Semua rusuk pada kubus memiliki panjang yang sama.[/*][*][b]Jumlah rusuk:[/b] Kubus memiliki 12 rusuk yang saling berpotongan.[/*][*][b]Jumlah sudut:[/b] Kubus memiliki 8 titik sudut (titik pertemuan antara tiga rusuk).[/*][*][b]Simetri:[/b] Kubus memiliki simetri yang tinggi, yaitu simetri rotasi dan simetri refleksi.[/*][*][b]Diagonal:[/b] Kubus memiliki dua jenis diagonal:[/*][/list][list][*][b]Diagonal bidang[/b] (diagonal yang menghubungkan dua titik pada satu sisi persegi).[/*][*][b]Diagonal ruang[/b] (diagonal yang menghubungkan dua titik yang saling berlawanan di dalam kubus).[/*][/list]
5.3 Luas Permukaan Kubus
Luas permukaan kubus adalah jumlah luas dari seluruh permukaan yang membentuk kubus.
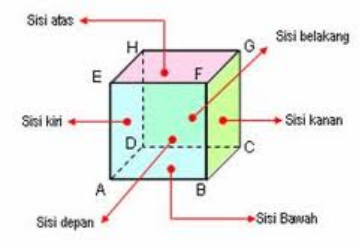
[justify]Untuk memahami konsep luas permukaan dari bangun ruang ini, kita perlu mengetahui bahwa kubus memiliki enam buah sisi yang berbentuk persegi. Luas permukaan bangun ruang ini adalah total luas dari enam sisi tersebut, yang digambarkan dengan rumus berikut:[/justify][br][br][center][size=200][size=100][b]Rumus untuk menghitung luas permukaan kubus adalah:[br][br][math]L=6\times S^2[/math][/b][/size][/size][/center][br][br]Keterangan:[br]L = luas permukaan kubus[br]S = panjang sisi kubus[*][br][/*][br]Jadi, untuk menghitung luas permukaan kubus, kamu tinggal mengkuadratkan panjang sisi kubus dan mengalikan hasilnya dengan 6.[br]
5.4 Contoh Soal
[i][b]Contoh 1:[br][/b][/i][br]Sebuah kubus memiliki panjang sisi 2 m. Tentukan luas permukaan kubus tersebut!
[i][b]Penyelesaian:[/b][/i][br]Diketahui:[br]Panjang rusuk (s) = 2m[br][br]Ditanya:[br]Berapakah luas permukaan kubus diatas?[br][br][i][u][b]Jawab:[/b][/u][/i][br][math]Lp.Kubus=6\times s^2=6\times\left(2\right)^2=6\times4=24m^2[/math][br][br]Jadi, luas permukaan kubus diatas adalah [math]24m^2[/math]
[i][b]Contoh 2:[br][br][/b][/i][justify]Sebuah benda berbentuk kubus memiliki luas permukaan 294 cm². Maka panjang sisi benda tersebut adalah …[/justify]
Luas permukaan = 294 [math]cm^2[/math]
[i][b]Penyelesaian:[/b][/i][br]Diketahui:[br]Luas permukaan kubus= 294 [math]cm^2[/math][br][br]Ditanya:[br]Berapa panjang sisi kubus diatas?[br][br][i][b]Jawab:[/b][/i][br][math]Lp.Kubus=6\times s^2[/math][br][math]s^2=Lp.Kubus\div6[/math][br][math]s=\sqrt{Lp.Kubus\div6}[/math][br][math]s=\sqrt{294\div6}[/math][br][math]s=\sqrt{49}=7cm[/math][br]Jadi panjang sisi kubus diatas adalah [math]7cm[/math]
Setelah memahami contoh di atas, kita akan menemukan berbagai cara untuk menghitung luas permukaan kubus. Baca dan pahami contoh di bawah ini untuk membantumu memahami formula untuk menghitung luas permukaan kubus!
5.5 Latihan!
1. Sebuah kotak berbentuk kubus memiliki panjang rusuk 8 cm. Berapa luas karton yang dibutuhkan untuk membuat kotak tersebut?[br][br]
2. Sebuah kubus memiliki luas permukaan 150 cm². Tentukan panjang rusuk kubus tersebut!
3. Sebuah kubus memiliki luas permukaan yang sama dengan luas permukaan sebuah balok berukuran 10 cm x 8 cm x 6 cm. Tentukan panjang rusuk kubus tersebut!
Pada bab ini, siswa akan mempelajari bentuk dan bagian-bagian dari balok, salah satu bangun ruang sisi datar yang banyak dijumpai dalam kehidupan sehari-hari, seperti kotak tisu, lemari, atau kardus. Balok memiliki 6 sisi berbentuk persegi panjang, 12 rusuk, dan 8 titik sudut. Berbeda dengan kubus, balok memiliki sisi-sisi yang bisa berbeda panjang. Pemahaman tentang bentuk, ukuran sisi, dan struktur balok menjadi dasar penting sebelum siswa mempelajari cara menghitung luas permukaannya secara menyeluruh.
[justify]Apa itu Luas Permukaan Balok?[br][br][b][i][/i][/b][b]Luas permukaan balok[/b] adalah ukuran total dari seluruh bidang luar yang menutupi balok. Balok memiliki enam sisi, dan setiap sisinya berbentuk persegi panjang. Sisi-sisi ini tersusun berpasang-pasangan: atas dan bawah, depan dan belakang, serta kiri dan kanan. Luas permukaan balok menggambarkan seberapa besar bidang datar yang dibutuhkan untuk membungkus balok itu secara keseluruhan, seperti saat kita ingin membungkus kotak sabun atau kardus berbentuk persegi panjang dengan kertas.[br][/justify]Perhatikan dan amati animasi dibawah ini!
[justify]Animasi ini memvisualisasikan pembentukan balok dari jaring-jaringnya. Jaring-jaring balok terdiri dari enam persegi panjang yang akan dilipat menjadi sisi-sisi balok. Luas permukaan balok adalah total luas keenam persegi panjang penyusunnya. Jika panjang, lebar, dan tinggi balok berturut-turut adalah [math]p[/math], [math]l[/math], dan [math]t[/math], maka luas permukaannya dihitung dengan menjumlahkan luas setiap pasang sisi yang identik: [math]2(pl+lt+pt)[/math]. Animasi ini memperlihatkan bagaimana setiap komponen dari jaring-jaring, yang merepresentasikan luas masing-masing sisi balok, berkontribusi pada luas permukaan total balok ketika dilipat menjadi bangun ruang tiga dimensi. Dengan mengamati animasi, kita dapat memahami bahwa luas permukaan balok adalah jumlah dari luas keenam sisi persegi panjang penyusunnya.[br][br]Balok adalah bentuk yang sangat umum dan sering kita temui dalam kehidupan sehari-hari. Contoh nyata balok dalam kehidupan sehari-hari menunjukkan bagaimana bentuk balok digunakan dalam berbagai benda yang sering kita temui, seperti kotak sepatu, lemari, dan sebagainya.[/justify]
(a) kotak sepatu
[size=100][justify]Salah satunya yaitu [b]kotak sepatu[/b]. Kotak sepatu memiliki bentuk yang sesuai dengan definisi balok, yaitu bangun ruang tiga dimensi dengan enam sisi berbentuk persegi panjang. Dimensi kotak sepatu, seperti panjang, lebar, dan tinggi, juga mencerminkan dimensi balok. Dengan demikian, kotak sepatu merupakan contoh nyata dari balok dalam kehidupan sehari-hari.[/justify][/size]
(b) lemari
[justify][size=100]Selain itu, [b]Lemari[/b] juga memiliki bentuk yang menyerupai balok, dengan enam sisi yang berbentuk persegi panjang, 12 rusuk, dan 8 titik sudut. Sama seperti balok, lemari juga memiliki sudut siku-siku (90 derajat) di setiap pertemuan sisi dan tiga dimensi utama (panjang, lebar, dan tinggi). Oleh karena itu, lemari dapat dianggap sebagai contoh nyata dari balok dalam kehidupan sehari-hari.[/size][br][/justify][size=100]Balok menjadi bentuk yang ideal karena kesederhanaannya dan kemampuannya untuk menyimpan atau menyusun barang dengan efisien.[/size]
6.2 Sifat-sifat Balok
Beberapa sifat balok yang perlu diketahui, antara lain:
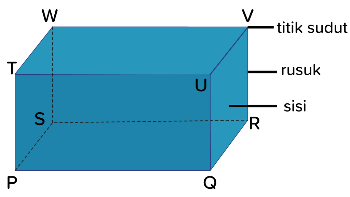
[justify][/justify][list=1][*][b]Jumlah sisi:[/b] Balok memiliki 6 sisi, dan masing-masing sisi berbentuk persegi panjang.[br][br][/*][*][b]Jumlah rusuk:[/b] Balok memiliki 12 rusuk, terdiri dari 4 rusuk panjang, 4 rusuk lebar, dan 4 rusuk tinggi.[br][br][/*][*][b]Jumlah sudut:[/b] Balok memiliki 8 titik sudut, yaitu titik pertemuan dari 3 rusuk.[br][br][/*][*][b]Pasangan sisi yang sejajar:[/b] Balok memiliki 3 pasangan sisi yang saling sejajar dan memiliki ukuran yang sama.[/*][br][*][b]Diagonal sisi:[/b] Diagonal pada sisi balok menghubungkan dua titik yang berlawanan pada satu sisi persegi panjang.[br][br][/*][*][b]Diagonal ruang:[/b] Diagonal ruang pada balok menghubungkan dua titik yang berlawanan di dalam balok.[br][/*][/list]
6.3 Luas Permukaan Balok
Luas permukaan balok adalah jumlah seluruh luas sisi-sisi balok. Sebuah balok memiliki 6 sisi, yang terdiri dari pasangan sisi yang saling berlawanan. Untuk menghitung luas permukaan balok, kita perlu mengetahui panjang, lebar, dan tinggi balok.
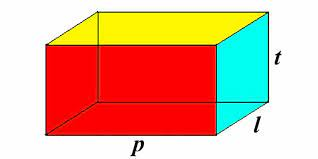
[justify][b][/b][/justify][center][/center][center][b]Rumus untuk menghitung luas permukaan balok adalah:[br][/b][math]LuasPermukaan=2×(p×l+p×t+l×t)[/math][/center]
[justify]Keterangan:[br] [math]p=[/math] Panjang Balok[br] [math]l=[/math] Lebar Balok[br] [math]t=[/math] Tinggi Balok[br][br]Jadi, kita mengalikan setiap pasangan dimensi dan menjumlahkan hasilnya, lalu mengalikan dengan 2 karena ada dua sisi untuk setiap pasangan dimensi.[/justify]
6.4 Contoh soal
[justify][b][i]Contoh 1:[/i][/b][br][br]Sebuah balok memiliki panjang 24 cm, lebar 6 cm, dan tinggi 8 cm. Hitunglah luas permukaan balok tersebut![/justify]
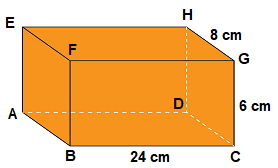
[b][i]Penyelesaian:[/i][/b][br]Diketahui:[br]Panjang Balok: 24 cm[br]Lebar Balok: 8 cm[br]Tinggi Balok: 6 cm[br][br]Ditanya:[br]Berapakah luas permukaan balok diatas?[br][br][b][i][u]Jawab:[br][/u][/i][/b][math]LuasPermukaan=2×(p×l+p×t+l×t)[/math][br][math]LuasPermukaan=2×(24×8+24×6+8×6)[/math][br][math]LuasPermukaan=2×(192+144+48)[/math][br][math]LuasPermukaan=2×384[/math][br][math]LuasPermukaan=768cm^2[/math][br]Jadi, luas permukaan kubus di atas adalah [math]768cm^2[/math]
[justify][b][i]Contoh 2:[br][br][/i][/b]Dani memiliki sebuah akuarium di rumahnya yang berbentuk balok. Akuarium tersebut terbuat dari kaca dan digunakan untuk memelihara ikan hias. Setelah beberapa bulan, bagian luar kaca mulai tampak kusam dan perlu dibersihkan serta dicat ulang agar terlihat lebih menarik. Akuarium itu memiliki ukuran panjang 40 cm, lebar 25 cm, dan tinggi 30 cm. Sebelum mulai mengecat, Dani ingin mengetahui berapa luas permukaan seluruh bagian luar akuarium tersebut yang harus dibersihkan dan dicat. Untuk itu, Dani perlu menghitung [b]luas permukaan balok[/b] dari akuarium miliknya. Hitunglah luas permukaan akuarium tersebut untuk membantu Dani merencanakan jumlah cat dan alat pembersih yang diperlukan![br][br][b][i]Penyelesaian:[/i][/b][br]Diketahui:[br]Panjang balok = 40 cm[br]lebar balok = 25 cm[br]tinggi balok = 30 cm[br][br]Ditanya:[br]Berapakah luas permukaan akuarium tersebut?[br][br][b][i][u]Jawab:[/u][/i][/b][br][math]LuasPermukaan=2×(p×l+p×t+l×t)[/math][br][math]LuasPermukaan=2×(40×25+40×30+25×30)[/math][br][math]LuasPermukaan=2×(1000+1200+750)[/math][br][math]LuasPermukaan=2×(2.950)[/math][br][math]LuasPermukaan=5.900cm^2[/math][br]Jadi, luas permukaan akuarium tersebut adalah [math]5.900cm^2[/math][br][br][br]Jika masih belum memahami materi ini dengan baik, silakan klik tautan video YouTube di bawah ini dan tontonlah penjelasannya dengan saksama. Video tersebut akan membantu memperjelas konsep yang telah dibahas.[/justify]
6.5 Latihan Soal
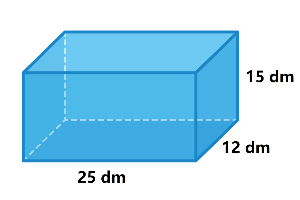
1. Hitunglah Luas permukaan gambar di atas!
[justify]2. Sebuah balok memiliki lebar 10 cm dan tinggi 8 cm. Luas permukaan balok tersebut adalah 616 cm². Berapakah panjang balok tersebut?[/justify]
3. Suatu balok memiliki luas permukaan[math]180cm^2[/math]. Jika panjang dan lebar balok masing-masing 8 cm dan 6 cm. tentukan tinggi balok tersebut!
Pada bab ini, siswa akan mempelajari prisma, yaitu bangun ruang sisi datar yang memiliki dua bidang alas yang kongruen dan sejajar, serta sisi-sisi tegak berbentuk persegi panjang. Bentuk alas prisma dapat berupa segitiga, segiempat, atau segibanyak lainnya, sehingga terdapat berbagai jenis prisma, seperti prisma segitiga, prisma segiempat, dan sebagainya. Dengan memahami bagian-bagian penyusun prisma—alas, tutup, dan sisi tegak—siswa akan lebih siap untuk mempelajari cara menghitung luas permukaan prisma sesuai bentuk alasnya.
[justify]Apa itu Luas Permukaan Limas?[br][br][b]Luas permukaan prisma[/b] adalah ukuran seluruh bidang luar yang membungkus sebuah prisma. Artinya, ini adalah total luas dari semua sisi yang tampak dari luar prisma, termasuk dua bidang alas yang sama bentuk dan ukurannya, serta bidang-bidang tegak yang menghubungkan kedua alas tersebut.[br][br]Sederhananya, Bayangin kamu punya sebuah kotak segitiga atau segiempat yang terbuat dari karton. Kalau kamu mau membungkus seluruh permukaannya dengan kertas, luas permukaan prisma itu adalah jumlah seluruh kertas yang kamu butuhkan untuk menutupi bagian luarnya.[/justify]Perhatikan dan amati animasi dibawah ini!
[justify]Animasi ini menggambarkan pembentukan prisma segitiga dari jaring-jaringnya. Jaring-jaring prisma segitiga terdiri dari dua segitiga identik (alas dan tutup) serta tiga persegi panjang (sisi tegak). Luas permukaan prisma segitiga adalah total luas kedua segitiga dan ketiga persegi panjang tersebut. Animasi ini secara visual menunjukkan bagaimana komponen-komponen jaring-jaring ini dilipat dan bergabung untuk membentuk permukaan luar prisma segitiga. Luas kedua segitiga dihitung berdasarkan alas dan tingginya, sementara luas setiap persegi panjang sisi tegak dihitung berdasarkan salah satu sisi segitiga sebagai alas dan tinggi prisma sebagai tingginya. Dengan demikian, animasi ini secara efektif memvisualisasikan dekomposisi luas permukaan prisma segitiga menjadi luas dua alas segitiga dan luas ketiga sisi tegak persegi panjangnya, dan sebaliknya, bagaimana bagian-bagian ini membentuk luas total permukaan prisma ketika dilipat menjadi bangun ruang. Anda dapat melihat bagaimana setiap komponen dari jaring-jaring berkontribusi pada luas keseluruhan prisma.[br][br]Prisma banyak ditemukan dalam kehidupan sehari-hari, baik secara langsung maupun sebagai bentuk dasar dari berbagai benda. Dalam kehidupan sehari-hari, bentuk prisma sering kita temukan dalam berbagai benda, seperti:[br][br](a) Kotak susu[br][/justify]
[justify][size=100][b]Kotak susu [/b]merupakan salah satu contoh prisma segiempat (balok), karena memiliki alas dan atap berbentuk persegi panjang dan sisi tegak yang juga berupa persegi panjang. Kotak susu dirancang seperti ini agar mudah disusun dan disimpan di rak.[br][br](b) Tempat pensil segitiga[/size][/justify]
[justify][size=100]Selain itu, [b]Tempat pensil segitiga [/b]juga merupakan contoh prisma segitiga juga. Bentuk ini sering dipilih karena unik dan fungsional, serta mudah dibawa.[/size][/justify]
8.2 Sifat-sifat Prisma
[*][b]1. Memiliki dua bidang alas yang kongruen dan sejajar.[/b][br]Alas ini berbentuk segi banyak (segitiga, segiempat, segilima, dll) dan bentuknya sama persis antara alas bawah dan alas atas.[/*][*][b]2. Sisi tegaknya berbentuk persegi panjang.[/b][br]Sisi-sisi tegak ini menghubungkan sisi-sisi yang bersesuaian dari kedua alas.[/*][*][b]3. Jumlah sisi tergantung pada bentuk alasnya.[/b][br]Jika alasnya segitiga, maka prisma memiliki 5 sisi. Jika alasnya segiempat, maka prismanya memiliki 6 sisi, dan seterusnya.[/*][*][b]4. Memiliki rusuk yang tegak dan rusuk yang sejajar dengan alas.[/b][br]Rusuk tegak menghubungkan titik-titik pada alas bawah dan atas. Semua rusuk sejajar antara satu sisi dengan sisi lainnya yang sejenis.[/*][*][b]5. Memiliki titik sudut yang jumlahnya dua kali lipat dari jumlah sisi alas.[/b][br]Misalnya, prisma segitiga memiliki 6 titik sudut, karena segitiga punya 3 titik sudut, dan prisma segitiga punya dua alas.[/*][*][b]6. Memiliki bentuk yang simetris dan stabil.[/b][br]Ini membuat prisma sering digunakan dalam benda-benda sehari-hari karena bentuknya efisien dan mudah disusun.[/*]
8.3 Luas Permukaan Prisma
Luas permukaan [b]prisma[/b] secara umum dapat dihitung dengan rumus:[br][b][center][i][br]Luas Permukaan Prisma = 2 × Luas Alas + Luas Seluruh Sisi Tegak[/i][/center][/b][br]Secara lebih rinci:[br]Misalkan:[br][b]Luas alas[/b] = [math]La[/math][br][b]Keliling alas [/b]=[math]K[/math][br][b]Tinggi Prisma =[math]t[/math][br][br][/b]Maka, Rumus Umum :[br][br][b][i][center]Luas Permukaan Prisma=[math]2La+K×t[/math][br][/center][/i][/b][br]Penjelasan:[br][b]2 [/b][b]× Luas Alas[/b]: karena prisma punya dua alas yang kongruen (identik)[br][b]Keliling alas × tinggi[/b]: ini menjumlahkan seluruh sisi tegak (selimut prisma), karena setiap sisi tegak itu berbentuk persegi panjang.[br][br]Beberapa [b]rumus luas permukaan prisma[/b] berdasarkan [b]jenis alasnya[/b]:[br][br]1. Prisma Segitiga:[br][br][i][b][center]Luas Permukaan= 2 × Luas Segitiga + Keliling Segitiga × Tinggi Prisma[/center][/b][/i][center][math]=2\times\left(\frac{1}{2}\times a\times t\right)+(a+b+c)×T[/math][/center]2. Prisma Segiempat (misalnya alas berbentuk persegi panjang)[br][center][br][math]LuasPermukaan=2×(p×l)+2×(p+l)×T[/math][/center][br]3. Prisma Segi-n (n-sisi)[br][center][br][math]LuasPermukaan=2×LuasAlas+KelilingAlas×TinggiPrisma[/math][/center]Bentuk ini digunakan kalau alasnya segilima, segienam, dll.[br]
8.4 Contoh Soal:
[i][b]Contoh 1:[br][br][/b][/i][justify]Prisma segitiga di bawah memiliki bentuk alas berupa segitiga sama kaki dengan alas 8 cm dan sisi miring 5 cm. Tinggi prisma yaitu 30 cm. Hitunglah Luas permukaan prisma![/justify]
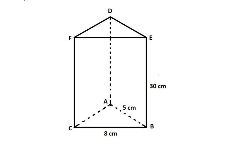
[b][i]Penyelesaian:[/i][/b][br][br]Diketahui:[br]Panjang sisi AB = 5 cm dan sisi CB = 8 cm, untuk mencari tinggi BT= (CB : 2 = 8 : 2 )= 4 cm. [br]Kita anggap titik di tengah antara C dan B adalah T.[br][br]Ditanya:[br]Berapa Luas Permukaan Prisma diatas?[br][br]Jawab:[br]Mencari tinggi segitiga (AT) dengan rumus pythagoras:[br][math]AB^2=BT^2+AT^2[/math][br][math]5^2=4^2+AT^2[/math][br][math]25=16+AT^2[/math][br][math]AT=\sqrt{25-16}[/math][br][math]AT=\sqrt{9}[/math][br][math]AT=3cm[/math][br]Mencari Luas Permukaan:[br][br][i]Luas Permukaan= 2 × Luas Segitiga + Keliling Segitiga × Tinggi Prisma[/i][br][math]LP.Prisma\bigtriangleup=2\times\left(\frac{1}{2}\times a\times t\bigtriangleup\right)+\left(ab+bc+ca\right)\times T.prisma[/math][br][math]LP.Prisma\bigtriangleup=2\times\left(\frac{1}{2}\times8\times3\right)+\left(8+5+5\right)\times30[/math][br][math]LP.Prisma\bigtriangleup=2\times\left(12\right)+\left(18\right)\times30[/math][br][math]LP.Prisma\bigtriangleup=24+540[/math][br][math]LP.Prisma\bigtriangleup=564cm^2[/math][br][br]Jadi luas permukaan prisma segitiga di atas sebesar 564 [math]cm^2[/math]
[b][i]Contoh 2:[br][/i][/b][br]Sebuah prisma segitiga memiliki penampang sebagai berikut:
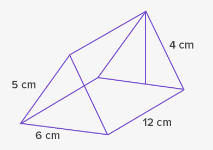
[size=100]Tentukan luas permukaan dan volume prisma tersebut.[/size]
[b][i]Penyelesaian:[br][br][/i][/b]Rumus:[br][br][i]Luas permukaan = (2 x luas alas) + (keliling alas x tinggi)[/i][br][br]Luas alas = [math]\frac{1}{2}\times alas\times tinggi=\frac{1}{2}\times6\times4=12cm^2[/math][br]Keliling alas =[math]6+5+5=16cm[/math].[br]Jadi, luas permukaan prisma = [math](2\times12)+(16\times12)=24+192=216cm^2[/math][br][br][br]Setelah memahami contoh di atas, kita akan menemukan berbagai cara untuk menghitung luas permukaan prisma. Baca dan pahami video di bawah ini untuk membantumu memahami rumus untuk menghitung luas permukaan prisma!
[justify]Video tersebut adalah panduan belajar menghitung luas permukaan prisma dengan tiga contoh soal berbeda: prisma segitiga siku-siku, segitiga dibaringkan, dan segitiga sama kaki. Video ini menjelaskan rumus umum luas permukaan prisma dan cara mencari luas serta keliling alas jika belum diketahui, sehingga pemirsa dapat menguasai perhitungan luas permukaan prisma dengan berbagai bentuk alas segitiga.[/justify]
8.5 Latihan Soal!
[justify]1. Sebuah prisma memiliki alas berbentuk segitiga siku-siku dengan panjang sisi siku-sikunya adalah 6 cm dan 8 cm. Tinggi prisma tersebut adalah 10 cm. Hitunglah luas permukaan prisma tersebut.[br][/justify]
[justify]2. Sebuah prisma memiliki alas berbentuk segitiga sama kaki dengan panjang sisi alasnya 10 cm dan panjang kedua sisi kakinya adalah 13 cm. Tinggi segitiga alas adalah 12 cm. Jika tinggi prisma tersebut adalah 15 cm, hitunglah luas permukaan prisma tersebut.[/justify]
[justify]3. Sebuah prisma memiliki alas berbentuk segitiga dengan panjang sisi-sisinya adalah 7 cm, 15 cm, dan 20 cm. Tinggi prisma tersebut adalah 12 cm. Hitunglah luas permukaan prisma tersebut. (Untuk soal ini, Siswa perlu menggunakan rumus Heron untuk mencari luas alas segitiga sembarang).[/justify]
Bab ini memperkenalkan limas, yaitu bangun ruang sisi datar yang memiliki satu bidang alas berbentuk segibanyak dan sisi-sisi tegak berbentuk segitiga yang bertemu di satu titik puncak. Jenis limas ditentukan berdasarkan bentuk alasnya, seperti limas segitiga, limas segiempat, dan lainnya. Dengan memahami struktur limas—terdiri dari alas dan sisi-sisi tegak—siswa akan lebih mudah mempelajari cara menghitung luas permukaan limas dengan mempertimbangkan bentuk alas dan luas masing-masing sisi tegaknya.
[justify]Apa itu Luas Permukaan Limas?[br][br][b]Luas permukaan limas[/b] adalah total dari seluruh luas bidang yang menyusun permukaan luar limas. Limas sendiri adalah bangun ruang yang memiliki satu bidang alas berbentuk segi banyak (bisa segitiga, segiempat, dan seterusnya) dan sisi-sisi tegaknya berbentuk segitiga yang bertemu di satu titik puncak.[br][br]Jadi, untuk membayangkannya, kita bisa membayangkan seperti membungkus limas dengan kertas: bagian kertas yang digunakan untuk membungkus seluruh permukaannya, baik alas maupun sisi-sisi segitiga di sampingnya, itulah yang disebut luas permukaan limas. Setiap sisi yang tampak dari luar limas, termasuk alas dan sisi-sisi tegaknya, semuanya dihitung sebagai bagian dari luas permukaan.[/justify]Perhatikan dan amati animasi dibawah ini!
[justify]Animasi ini menggambarkan pembentukan limas segi empat dari jaring-jaringnya. Jaring-jaring limas segi empat terdiri dari sebuah alas berbentuk segi empat dan empat segitiga yang akan menjadi sisi-sisi tegaknya. Luas permukaan limas segi empat adalah jumlah luas alas dan luas keempat sisi tegaknya. Animasi ini secara visual menunjukkan bagaimana komponen-komponen jaring-jaring ini menyatu untuk membentuk permukaan luar limas. Luas alas dihitung sesuai dengan bentuk segi empatnya, sementara luas setiap sisi tegak segitiga bergantung pada alas dan tingginya. Dengan demikian, animasi ini secara efektif memvisualisasikan dekomposisi luas permukaan limas segi empat menjadi luas alas segi empat dan luas keempat segitiga sisi tegaknya, dan sebaliknya, bagaimana bagian-bagian ini membentuk luas total permukaan limas ketika dilipat menjadi bangun ruang. Anda dapat melihat bagaimana setiap komponen dari jaring-jaring berkontribusi pada luas keseluruhan limas.[/justify][br]Limas adalah bangun ruang tiga dimensi yang memiliki satu alas berbentuk segi banyak dan sisi-sisi lainnya berupa segitiga yang bertemu pada satu titik puncak. Bentuk limas bisa ditemukan dalam berbagai benda nyata di sekitar kita.[br][br](a) Tenda pramuka berbentuk segitiga
[justify][size=100][/size][/justify][justify][size=100]Salah satu contoh nyata limas adalah [b]tenda pramuka berbentuk segitiga[/b]. Bagian bawah tenda berfungsi sebagai alas, sedangkan sisi-sisi miringnya yang menjulang ke atas membentuk segitiga yang bertemu di bagian atas sebagai puncak. Contoh lain adalah [b]bangunan piramida di Mesir[/b], yang memiliki alas persegi dan sisi-sisi samping berbentuk segitiga yang meruncing ke atas.[br][br](b) Kap lampu hias[/size][/justify]
[justify][size=100]Selain itu, bentuk limas juga bisa kita temui pada [b]kap lampu hias[/b], [b]kerucut es krim bagian atas (jika berbentuk segitiga)[/b], atau [b]hiasan meja berbentuk piramida[/b]. Benda-benda ini tidak hanya memiliki nilai estetika, tetapi juga secara tidak langsung memperkenalkan konsep limas dalam kehidupan sehari-hari.[/size][/justify]
7.2 Sifat-sifat Limas
[justify]Berikut merupakan sifat-sifat dari bangun limas, antara lain:[br][br][b]1. Memiliki satu buah alas[br][/b]Alas limas berbentuk segi banyak, seperti segitiga, segiempat, atau bentuk lainnya sesuai jenis limasnya.[br][br][b]2. [/b][b]Memiliki sisi tegak berbentuk segitiga[br][/b]Semua sisi tegak limas berbentuk segitiga dan masing-masing bertemu pada satu titik puncak.[br][br][b]3. [/b][b]Memiliki satu titik puncak[br][/b]Titik puncak adalah tempat bertemunya semua sisi tegak limas di bagian atas.[br][br][b]4. [/b][b]Jumlah sisi limas tergantung bentuk alasnya[br][/b]Jika alasnya segitiga, maka jumlah sisi limas ada 4 (1 alas dan 3 sisi tegak). Jika alasnya segiempat, maka jumlah sisinya 5 (1 alas dan 4 sisi tegak), dan seterusnya.[br][br][b]5. [/b][b]Jumlah rusuk limas tergantung pada jumlah sisi alasnya[br][/b]Jumlah rusuk sama dengan jumlah sisi alas ditambah jumlah sisi tegak, karena tiap titik sudut alas terhubung ke puncak.[br][br][b]6. [/b][b]Jumlah titik sudut limas tergantung pada alasnya ditambah satu[br][/b]Titik sudut limas terdiri dari titik-titik pada alas dan satu titik puncak di atas.[br][br][b]7. Tidak memiliki sisi yang sejajar[br][/b]Berbeda dengan bangun ruang seperti prisma, limas tidak memiliki pasangan sisi yang sejajar.[/justify]
7.3 Luas Permukaan Limas
[center]Rumus umum luas permukaan limas yaitu sebagai berikut:[br][math]LP.Limas=LuasAlas+JumlahLuasSisiTegak[/math][/center]Sisi tegak pada limas berbentuk segitiga, jadi luasnya dihitung seperti luas segitiga.[br][br]Berdasarkan jenis alasnya, luas permukaan limas dibagi menjadi berikut:[br][i][br][b]1. [/b][b]Limas Segitiga[/b][br](Alas berbentuk segitiga, memiliki 3 sisi tegak)[/i][br][center][i][br]Luas Permukaan = Luas alas segitiga + Jumlah luas 3 sisi tegak[/i][/center][i][b]2. Limas Segiempat (misalnya alas persegi)[/b][br](Alas berbentuk persegi, memiliki 4 sisi tegak)[/i][br][center][br][math]\text{Luas Permukaan}=s\times s+4\times\left(\frac{1}{2}\times s\times t\right)[/math][/center][b]Keterangan:[/b][br]s = panjang sisi alas[br]t = tinggi sisi tegak (segitiga)[br][i][br][b]3. Limas Segilima[/b][br](Alas berbentuk segilima, memiliki 5 sisi tegak)[br][br][center]Luas Permukaan=Luas alas segilima + Jumlah luas 5 sisi tegak[/center][/i][i][b]4. Limas Segienam[br][/b](Alas berbentuk segienam, memiliki 6 sisi tegak[br][br][center]Luas Permukaan=Luas alas segienam + Jumlah luas 6 sisi tegak[/center][/i]
7.4 Contoh Soal
[justify][b][i]Contoh Soal 1:[br][/i][/b][br]Limas di bawah mempunyai alas berbentuk persegi dengan sisi 10 cm, tinggi 12 cm dan sisi miring 13 cm. Luas permukaan limas tersebut adalah ... cm[sup]2[/sup].[/justify]
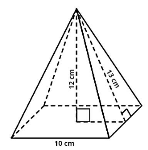
[size=100][b][i]Penyelesaian:[/i][/b][br]Diketahui:[*]Sisi persegi (s): 10 cm[/*][*]Tinggi sisi tegak: 12 cm[/*][*]Sisi miring Δ: 13 cm[/*]Ditanya:[br]Berapa luas permukaan limas tersebut?[/size][size=100][br][br][b][i]Jawab:[br][/i][/b]LP.Limas = Luas Alas + Jumlah 4 luas sisi tegak[br][math]LP.Limas=s\times s+\left(4\times\left(\frac{1}{2}\times a\times sisimiring\right)\right)[/math][br][math]LP.Limas=100+\left(4\times\left(\frac{1}{2}\times10\times13\right)\right)[/math][math]LP.Limas=100+\left(4\times\left(\frac{130}{2}\right)\right)[/math][math]LP.Limas=100+\left(4\times\left(65\right)\right)[/math][math]LP.Limas=100+\left(260\right)[/math][br][math]LP.Limas=360cm^2[/math][/size]
[b][i]Contoh 2:[br][br][/i][/b]Sebuah limas piramida alasnya berbentuk segitiga dengan panjang AC = 3 cm, BC = 4 cm, dan AB = 5 cm. Apabila tinggi limas 10 cm. Apakah luas permukaannya bisa ditentukan?
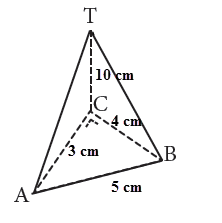
[justify][size=100][b][i][/i][/b][/size][/justify][size=100][justify][b][i]Penyelesaian:[/i][/b][br]Diketahui:[br]Alas Segitiga ABC[br]AC= 3 cm[br]BC= 4 cm[br]AB= 5 cm[br]Tinggi Limas = 10 cm[br][br]Ditanya:[br]Berapakah Luas Permukaan Piramida tersebut?[br][br][b][i]Jawab:[br][/i][/b][b]1. Luas Alas (Segitiga ABC):[/b][br]Karena kita mengetahui panjang ketiga sisi segitiga alas (3 cm, 4 cm, dan 5 cm), kita dapat menggunakan rumus Heron untuk mencari luasnya. Pertama, hitung semi-perimeter (s):[br][math]s=\frac{ac+bc+ab}{2}=\frac{\left(3+4+5\right)}{2}=6cm[/math][br]Kemudian, gunakan rumus Heron untuk luas (L.alas):[br][math]L.alas=\sqrt{s\left(s-ac\right)\left(s-bc\right)\left(s-ab\right)}[/math][br][math]L.alas=\sqrt{6\left(6-3\right)\left(6-4\right)\left(6-5\right)}[/math][br][math]L.alas=\sqrt{6\times\left(3\right)\times\left(2\right)\times\left(1\right)}[/math][br][math]L.alas=\sqrt{36}=6cm^2[/math][br][br][b]2. Luas Sisi Tegak:[/b][br]Piramida ini memiliki tiga sisi tegak yang berbentuk segitiga: TAB, TBC, dan TAC. Kita perlu menghitung luas masing-masing segitiga ini. Kita sudah mengetahui tinggi masing-masing sisi tegak dari titik T ke alas (10 cm). Kita juga mengetahui panjang alas dari masing-masing segitiga tegak (AB = 5 cm, BC = 4 cm, AC = 3 cm).[br][b]Luas Segitiga TAB (L.TAB):[/b][br][math]L.TAB=\frac{1}{2}×alas×tinggi=\frac{1}{2}×AB×tinggipiramida=\frac{1}{2}×5×10=25cm^2[/math][br][b]Luas Segitiga TBC (L.TBC):[/b][br][math]L.TBC=\frac{1}{2}×alas×tinggi=\frac{1}{2}×BC×tinggipiramida=\frac{1}{2}×4×10=20cm^2[/math][br][b]Luas Segitiga TAC (L.TAC):[/b][br][math]L.TAC=\frac{1}{2}×alas×tinggi=\frac{1}{2}×AC×tinggipiramida=\frac{1}{2}×3×10=15cm2[/math][br][b]3. Luas Permukaan Total (L.total):[/b][br]Jumlahkan luas alas dan luas ketiga sisi tegak:[br][math]L.total=L.alas+L.TAB+L.TBC+L.TAC=6+25+20+15=66cm^2[/math][br]Jadi, luas permukaan piramida tersebut adalah [math]66cm^2[/math].[br][br][br][br]Sebelum masuk ke latihan soal, yuk tonton video pembelajaran terkait Luas Permukaan Limas segilima berikut di YouTube:[/justify][/size]
[justify]Dari video tersebut, kamu akan belajar:[br][br]Menghitung luas alas segilima, luas alas dihitung dengan 5 kali luas segitiga sama sisi. Tinggi segitiga sama sisi dihitung menggunakan teorema Pythagoras, dan didapatkan tinggi segitiga sama sisi. Kemudian, luas alas limas dihitung. Menghitung luas segitiga pada sisi tegak dan menghitung luas permukaan limas, luas permukaan limas dihitung dengan menjumlahkan luas alas dan lima kali luas segitiga pada sisi tegak.[br][/justify]
7.5 Latihan Soal!
[justify]1. Sebuah limas segiempat persegi dengan panjang sisi [math]10cm[/math] dengan dengan tinggi limas [math]12cm[/math], maka berapa nilai luas permukaan limas segiempat tersebut?[/justify]
[justify]2. Diketahui luas alas limas segiempat [math]16cm^2[/math] , dengan tinggi segitiga tegak senilai [math]3cm[/math]. Tentukan luas permukaan limas segitiga tersebut![/justify]
[justify]3. Limas segi enam beraturan memiliki luas alas [math]120cm^2[/math] dan luas segitiga tegak [math]30cm^2[/math] . Tentukan luas permukaan limas segi enam tersebut![/justify]
Information
Sauvegarde …
Toutes les modifications ont été sauvegardées
Erreur
Un problème de délai est survenu. Essayer à nouveau ...
Désolé, mais le serveur ne répond pas. Attendre quelques minutes, puis essayer de sauvegarder à nouveau.
