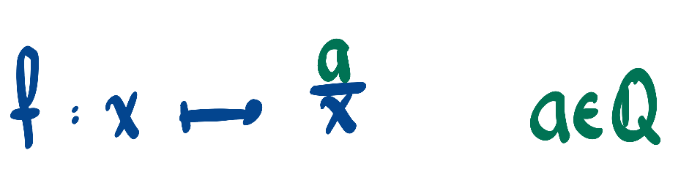
Auswirkungen von a
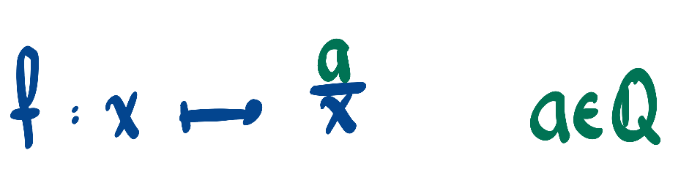
Untersuchung positiver Werte für a
Verändere den Schieberegler für a und beobachte, wie sich der Graph der Funktion ändert. [br]Beantworte damit die Fragen unterhalb
Zeichne den Graph von [math]g\left(x\right)=\frac{2}{x}[/math] und beschreibe, wie er aus dem Graphen von [math]f\left(x\right)=\frac{1}{x}[/math] hervorgeht.
Beschreibe allgemein, wie der Graph von [math]g\left(x\right)=\frac{a}{x}[/math] aus dem Graphen von [math]f\left(x\right)=\frac{1}{x}[/math] hervorgeht.
Beschreibe, wie sich die Asymptoten verändern.
Nun betrachten wir auch negative Werte
Verändere den Schieberegler für a und beobachte, wie sich der Graph der Funktion ändert. [br]Beantworte damit die Fragen unterhalb
Beschreibe, wie der Graph von [math]p\left(x\right)=\frac{-a}{x}[/math] aus dem Graphen von [math]g\left(x\right)=\frac{a}{x}[/math] hervorgeht.