Toni Kroos am Elfmeterpunkt ([url=https://www.eurosport.de/fussball/elfmeter-kroos-bietet-sich-an_sto5677253/story.shtml]https://www.eurosport.de/fussball/elfmeter-kroos-bietet-sich-an_sto5677253/story.shtml[/url], letzter Zugriff: 17.09.2019)
Binomialverteilung
Einführung
Zufallsexperimente, bei denen nur zwei Ausgänge (Treffer oder Niete, Erfolg oder Misserfolg) möglich sind, nennt man [b]Bernoulli-Experimente.[/b] Führt man ein Bernoulli-Experiment mehrfach durch, so spricht man von einer [b]Bernoulli-Kette[/b]. Heute geht es darum, die Formel herzuleiten, mit der man die Wahrscheinlichkeitsverteilung der Zufallsvariable X = "Anzahl der Treffer" bestimmen kann. Diese Verteilung nennen wir [i][b]Binomialverteilung[/b][/i].[br][br][br][br][br]
Kroos verwandelt in dieser Saison 15 von 20 Eltmetern.
[b]Düsseldorf. [/b]Beim gestrigen Länderspiel der Nationalmannschaft gegen Frankreich verwandelte Toni Kroos seinen 15. Elfmeter in dieser Saison und führte die Mannschaft damit zum Sieg. Fünf Mal konnte der Spieler in dieser Saison vom Elfmeterpunkt das Runde nicht ins Eck bringen. Laut Statistikern beträgt die Wahrscheinlichkeit bei einen Elfmeter ein Tor zu erzielen bei 75%, was mit der Erfolgsquote des Spielers übereinstimmt. Die Fans sind gespannt, ob der Sportler in den nächsten Wochen weiter erfolgreich Elfmeter verwandeln wird. [br][br](Fiktiver Zeitungsartikel)
Aufgabe 1
Die Wahrscheinlichkeit, dass ein Spieler einen Elfmeter verwandelt, beträgt p=0.75. [br][br][b]Bestimmen[/b] Sie die Wahrscheinlichkeit, dass der Spieler den Elfmeter verschießt. .
Aufgabe 2
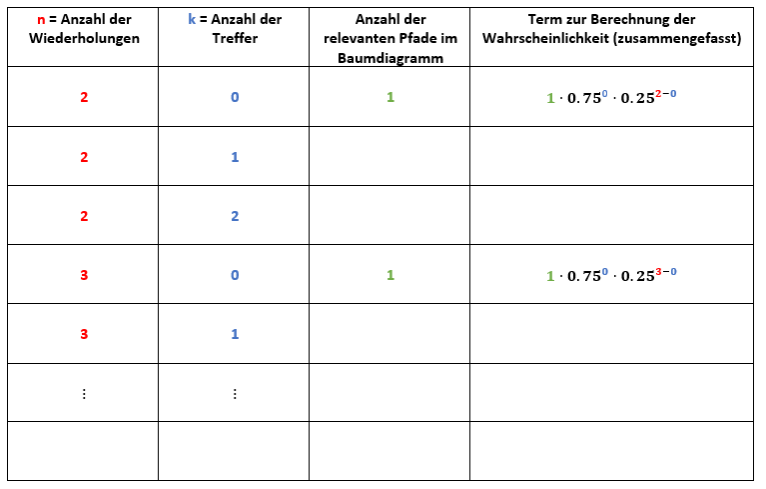
[b]Berechnen[/b] Sie die Wahrscheinlichkeit mit Hilfe eines Baumdiagramms (siehe unten), dass Toni Kross bei den nächsten zwei Elfmetern keinmal, einmal oder zweimal trifft. [b]Notieren [/b]Sie ihre Ergebnisse eine Tabelle. [br][br][i]Zur Kontrolle: Trennen Sie ihre Ergebnisse bei der Eingabe durch ein "-", z.B. 0.25-0.33-0.75. Runden Sie auf [b]zwei [/b]Nachkommastellen. [/i][br][br][b][i]Verwenden Sie die untenstehende Tabelle als Vorlage. [/i][/b]
Aufgabe 3
[b]Berechnen[/b] Sie nun die Wahrscheinlichkeit mit Hilfe eines Baumdiagramms (siehe unten), dass Toni Kroos bei den nächsten [b]drei[/b] Elfmetern keinmal, einmal, zweimal oder dreimal trifft. [b]Notieren [/b]Sie ihre Ergebnisse eine Tabelle. [br][br][i]Zur Kontrolle: Trennen Sie ihre Ergebnisse bei der Eingabe durch ein "-", z.B. 0.25-0.33-0.75. Runden Sie auf [b]zwei [/b]Nachkommastellen. [/i][br][br][b][i]Verwenden Sie die untenstehende Tabelle als Vorlage.[/i][/b]
Tempoaufgabe:
Betrachten Sie ihre Berechnungen in ihrer Tabelle. Können Sie Muster und Strukturen erkennen?
Aufgabe 4
Vergleichen Sie nun in ihrer Gruppe ihre Arbeitsergebnisse. Entwickeln Sie gemeinsam eine allgemeine Formel zur Berechnung der Wahrscheinlichkeit von [b]k[/b] Treffern bei [b]n [/b]Versuchen.
Aufgabe 5
Überprüfen Sie in Ihrer Gruppe ihre Formel, indem Sie drei Beispiele wählen und mittels des Taschenrechners berechnen. Überprüfen Sie ihre Lösung mit dem Geogebra-Applet. [br][br][i]Um ihre Ergebnisse zu überprüfen, variieren Sie die Größen [b]n[/b], [b]p [/b]sowie das [b]k [/b]in [math]P\left(k\le X\le k\right)[/math][/i].
Vertiefungsaufgabe
1) Bestimmen Sie mit Hilfe von Geogebra, wie groß die Wahrscheinlichkeit ist, dass Toni Kroos [b]mindestens [/b]17 Treffer bei 20 Elfmetern erzielt - gesucht ist also [math]P\left(X\ge17\right)[/math].[br][br]2) Bestimmen Sie mit Hilfe von Geogebra, wie groß die Wahrscheinlichkeit ist, dass Toni Kroos [b]höchstens[/b] 17 Treffer bei 20 Elfmetern erzielt, gesucht ist also [math]P\left(X\le17\right)[/math].