Geometría 7° básico
Este libro virtual tiene como propósito abordar los objetivos de aprendizaje desde el MA07 OA 10 hasta el MA07 OA 13, correspondientes al área de geometría. Los contenidos que se verán son exclusivos del plano, es decir, del 2D. Las propiedades geométricas que abarcan los objetivos de aprendizaje se abordarán bajo los conceptos de triangulación por construcción, transformación y descomposición.
Table of Contents
- Introducción
- Ángulos interiores
- Suma de los ángulos interiores de un triángulo
- Suma de los ángulos interiores de un cuadrilátero
- Suma de los ángulos interiores de un pentágono
- Ángulos exteriores
- Suma ángulos exteriores de polígonos convexos
- Área de un trapecio
- Área de un trapecio
- Área de un polígono regular
- Área de un polígono regular
- Área de un círculo
- Área del círculo
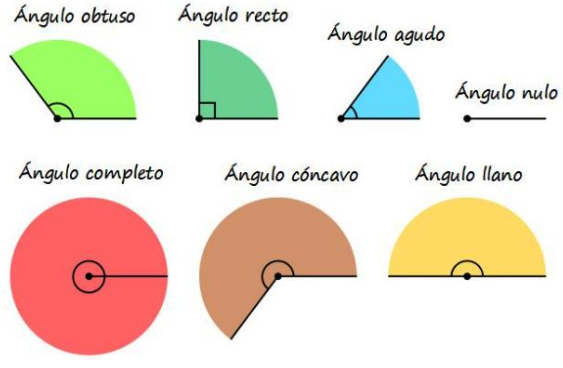
Suma de los ángulos interiores de un triángulo
Objetivo:
Descubrir cuánto suma los ángulos interiores de cualquier triángulo
Conceptos previos
Según la imagen anterior ¿Qué tipo de ángulo mide 180°?
Exploremos el comportamiento de los ángulos interiores de un triángulo
Profundicemos
Responde las siguientes preguntas por tu cuenta, para fortalecer tu aprendizaje.
Pregunta 1
Si mueves el punto rojo y modificas el triángulo, ¿qué sucede con la suma de sus ángulos interiores?
Pregunta 2
¿Cuánto suma los ángulos interiores de un triángulo? ¿Por qué?
Pregunta 3
¿Será posible construir un triángulo cuyos ángulos interiores son 30°, 60° y 100°? ¿Por qué?
Suma ángulos exteriores de polígonos convexos
Área de un trapecio
Objetivo:
Determinar el área de un trapecio.
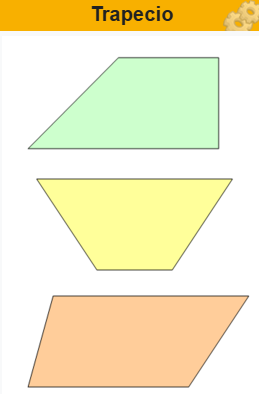
Utilidad de los trapecios
En arquitectura, los trapecios se utilizan principalmente en la construcción de techos y marquesinas. Debido a su forma, los trapecios permiten crear estructuras inclinadas que brindan una apariencia estética y también son funcionales para evacuar el agua de lluvia de manera eficiente
Conceptos previos
1. ¿Qué elementos se necesitan para determinar el área de un triángulo y un paralelogramo?
2. Seleccione la alternativa donde se exprese el área del triángulo y del paralelogramo respectivamente.
Exploremos el trapecio y sus elementos
Profundicemos
Responde las siguientes preguntas por tu cuenta, para fortalecer tu aprendizaje
Pregunta 1
Mueve los puntos A y B para crear tu propio trapecio. ¿Qué relación tienen el segmento rojo y el azul dentro de la figura del trapecio?
Pregunta 2
Para determinar el parea de triángulos, rectángulos y paralelogramos se necesita una base y su respectiva altura, ¿qué segmento coloreado será la base del trapecio?
Dafinición:
Los segmentos rojo y azul de cualquier trapecio se nombran como base menor y base mayor respectivamente.
Instrucciones
Presione el botón "Altura Trapecio" y escoja entre el botón "Copiar Trapecio" o el botón "Cortar trapecio"
Pregunta 3
Use el deslizador de rotación hasta el final, ¿en qué figura de transformó el trapecio?, ¿cuál es la base y altura de la nueva figura?
Pregunta 4
A partir de la figura final, ¿cómo se puede determinar el área del trapecio original?
Pregunta 5
Indique la alternativa que expresa el área de un trapecio
Pregunta 6
Dado un trapecio con base mayor 6 cm, base menor 7 cm y altura 8 cm. ¿Cuál es el área del trapecio?
Pregunta 7
Dado un trapecio con área 120 centímetros cuadrados, altura 6 cm y base menor 2 cm. ¿Cuál es la medida de la base mayor del trapecio?
Área de un polígono regular
[size=150]El área de un polígono regular puede calcularse mediante la fórmula siguiente[br][br][math]\Large{S=\frac{1}{2}Pa_p}[/math][br][br]Donde [i][b]P[/b][/i] es el perímetro de la figura y [i][b]a[sub]p[/sub][/b][/i] es su apotema, que se define como la distancia perpendicular desde el centro de la figura hasta uno de sus lados.[br][br]Podemos demostrar esta fórmula partiendo de la fórmula del área de un romboide. Para ello vemos que si cortamos nuestro polígono originar, colocamos sus partes, lo duplicamos y rellenamos los huecos, obtenemos un romboide cuya altura coincide con el apotema y su base es igual al perímetro del polígono original, sin embargo tiene doble de área.[/size]
Uso de la aplicación
El deslizador de la derecha permite modificar el número de lados de la figura y las casillas de verificación sirven para ocultar o mostrar la geometría del polígono original.[br][br]Los demás deslizadores y botones sirven para controlar la animación. Los botones activan o desactivan la reproducción automática. Los deslizadores, de izquierda a derecha, permiten animar manualmente, cambiar el tipo de animación (hacia atrás, hacia delante una vez, hacia delante continuo, oscilante) y la velocidad de reproducción automática.