
Sri Neni Amandus_ATURAN COSINUS
[center][b][u][/u][/b][/center][size=200][size=150][center][b][u]LKPD[br]ATURAN COSINUS (PADA SOAL JURUSAN TIGA ANGKA)[/u][/b][br][b](SMA)[/b][/center][/size][/size][b][br][color=#783f04]Tujuan Pembelajaran:[/color][/b][color=#783f04][br][br]1. Siswa belajar mengenai konsep trigonometri dalam segitiga sebarang, fokus pada aturan cosinus untuk [br] mengukur panjang sisi atau sudut.[br][br]2. Siswa dilatih menggunakan aturan cosinus dalam pemecahan masalah dunia nyata, meningkatkan [br] pemahaman siswa tentang penggunaan konsep trigonometri dalam situasi praktis.[br][br][br][b][u]Materi[br][/u][/b][b][br]Aturan Cosinus[br][/b][size=100][justify]Aturan cosinus adalah aturan yang menghubungkan antara nilai cosinus dan kuadrat panjang sisi pada salah satu sudut segitiga. Dengan kata lain, aturan cosinus berfungsi sebagai perbandingan panjang dalam suatu segitiga antara sisi samping sudut dengan sisi miringnya.[br][br]Dengan aturan ini, kita dapat menentukan besar salah satu sudut segitiga saat tiga sisi segitiga diketahui dan untuk menentukan salah satu sisi segitiga jika diketahui dua sisi dan dua sudutnya.[br][br]Pada segitiga sembarang ABC diketahui panjang masing-masing sisi adalah a, b, dan c dan ∠A, ∠B dan ∠C. Maka aturan cosinus yang berlaku yaitu:[/justify][/size][br][br][img]https://akcdn.detik.net.id/community/media/visual/2022/04/18/aturan-cosinus_169.png?w=620[/img][br][br][/color][b][url=https://www.youtube.com/watch?si=-Bx1gEvCOKslwSQA&v=eAYGH9_bpkM&feature=youtu.be]https://www.youtube.com/watch?si=-Bx1gEvCOKslwSQA&v=eAYGH9_bpkM&feature=youtu.be[/url][br][br][br]Petunjuk Pengerjaan Media:[br][/b][br]1. Membaca dan memahami soal yang telah diberikan yang berkaitan dengan dunia nyata.[br]2. Menginput nilai [math]\alpha,\beta[/math], dAB dan dBC yang tertera pada soal.[br]3. Selanjutnya siswa akan menginput nilai pada input box atau dengan menggeser slider dengan otomatis [br] untuk nilai sudut dan jarak yang ada pada soal yang telah diberikan.[br]4. Mengamati segitiga yang terbentuk setelah menginput nilai-nilai [math]\alpha,\beta[/math], dAB dan dBC pada [br] geogebra.[br]5. Setelah muncul nilai jarak (misalnya jarak Pelabuhan A ke Pelabuhan C). Siswa diminta memberikan [br] kesimpulan berdasarkan pengamatan yang telah dilakukannya pada gambar latihan.

[b]Jawablah soal-soal berikut ini dengan benar![/b]
1. Jelaskan konsep aturan cosinus yang kamu ketahui!
2. Bagaimana cara menghitung panjang salah satu sisi segitiga menggunakan aturan cosinus?
3. Tentukan jarak pelabuhan A ke pelabuhan C. Jika diketahui:[br][math][/math] a. [math]\alpha[/math]=[math]115^\circ[/math] , [math]\beta[/math]=[math]250^\circ[/math], dAB= 120 dan dBC= 100 [br] b. [math]\alpha[/math]=[math]90^\circ[/math], [math]\beta[/math]=[math]90^\circ[/math], dAB= 75 dan dBC= 110 [br] c. [math]\alpha[/math]=[math]360^\circ[/math], [math]\beta[/math]=[math]90^\circ[/math], dAB= 180 dan dBC= 90
4. Dari soal nomor 3, amati apakah segitiga tersebut selalu berubah bentuk dan segitiga apa saja yang [br] terbentuk setelah memasukkan nilai-nilainya!
Perhatikan gambar dibawah ini, untuk menjawab soal nomor 5!
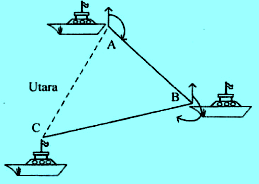
5. Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan jurusan tiga angka 120[math]^\circ[/math] sejauh 40 km, [br] kemudian berlayar menuju ke pelabuhan C dengan jurusan 240[math]^\circ[/math] sejauh 80 km. Maka berapakah jarak [br] antara pelabuhan C ke pelabhuan A?
Perhatikan gambar berikut untuk menjawab soal nomor 6!
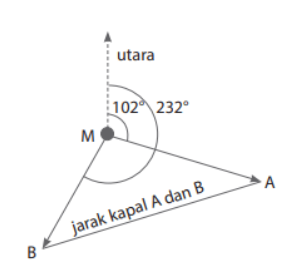
6. Dua buah kapal laut berangkat berlayar pada waktu yang bersamaan dari titik awal M. Kapal A bergerak [br] ke arah timur dengan sudut 102 ° (dari arah utara), sedangkan kapal B berlayar ke arah selatan dengan [br] besar sudut 232 ° (dari Utara). Apabila kapal A kecepatannya 30 km/jam, sedangkan kapal B [br] kecepatannya 45 km/jam. Tentukanlah jarak kedua kapal tersebut setelah berlayar selama 3 jam.
7. Jika sebuah segitiga ABC memiliki tiga sisi yaitu a, b, dan c. Jika sudut A,B, dan C adalah tiga sudut yang [br] berada di hadapan sisi a, b, dan c, maka aturan cosinus yang berlaku untuk segitiga tersebut adalah?
8. Amatilah segitiga yang terbentuk menggunakan media diatas jika nilai [math]\alpha,\beta[/math], dAB dan dBCnya sama. Misalkan [br] nilainya adalah 90[math]^\circ[/math] dan 90 km.
9. Mengapa penting untuk memahami aturan cosinus dalam pemecahan masalah trigonometri berdasarkan [br] materi yang telah diberikan?
10. Jelaskan kesimpulan utama dari aturan cosinus dan bagaimana konsep aturan cosinus dapat diterapkan [br] dalam berbagai situasi matematika dan kehidupan nyata!