Ein [b]Marktgleichgewicht[/b] besteht, wenn die Konsumenten genau so viel Ware kaufen wollen, wie es auf dem Markt gibt. Das heißt es bleibt keine Ware über und es ist auch niemand unzufrieden, weil er keine Ware bekommen hat. Wie viel Ware gekauft wird und wie viel Ware produziert wird, das wird über den Preis der Ware gesteuert. Wenn der Gleichgewichtspreis für ein Produkt verlangt wird, dann sind die Nachfrage und das Angebot ausgeglichen. [br][br]
Wie viel Ware wird gekauft? Je billiger ein Produkt ist, desto mehr wird gekauft. Die Nachfragefunktion [math]p_N(x)[/math] beschreibt diesen Zusammenhang zwischen dem [b]Preis[/b] einer Ware und dem möglichen [b]Absatz[/b]. Daher hat die Nachfragefunktion einen Funktionsgraphen, der mit steigender Warenmenge sinkt. Die Nachfragefunktion betrachtet das Marktgeschehen daher aus der [i]Perspektive des Verbrauchers[/i]. Wie bei der Preisfunktion im Monopol beschrieben, gibt es hier einen [b]Prohibitivpreis[/b] und eine [b]Sättigungsmenge[/b].
Wie viel Ware wird produziert? Die Angebotsfunktion [math]p_A(x)[/math] beschreibt den Zusammenhang des Preises eines Produktes mit der Menge des Produktes, die auf den Markt kommt. Je mehr Geld ein Anbieter für ein Produkt bekommt, desto mehr möchte er davon produzieren, oder desto mehr weitere Anbieter finden sich, die diese Ware auch produzieren möchten. Daher hat die Angebotsfunktion einen Funktionsgraphen, der mit steigender Warenmenge steigt. Die Angebotsfunktion betrachtet den Markt daher aus der Perspektive der Anbieter. Es gibt einen Preis einer Ware, unter dem es keinen Anbieter gibt, der bereit ist diese Ware zu produzieren. Das ist der Mindestpreis [math]p_M[/math].
Der Umsatz [math]U(x)[/math] ist das Geld, welches ein Unternehmen beim Verkauf der gesamten Ware erhalten hat, also gilt:[br][math]\Large{\boxed{U(x)=x\cdot p(x)}}[/math][br][br]Der Umsatz im Marktgleichgewicht ist damit [br][math]\Large{\boxed{U_{MGG}(x)=x_{GG}\cdot p_{GG}}}[/math][br][br]
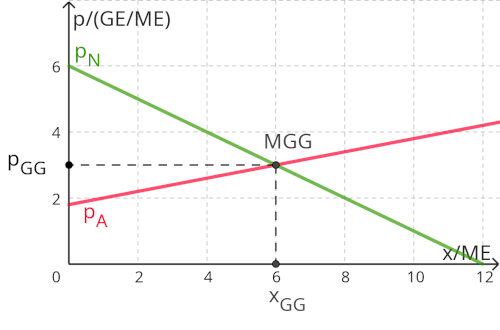
Dabei müssen [math]p_N(x)[/math] un [math]p_A(x)[/math] keine linearen Funktionen sein. [math]p_N[/math] ist irgend eine Funktion mit einem fallenden Funktionsgraphen und [math]p_A[/math] ist eine ansteigende Funktion.
1. Wie immer, wenn man Schnittpunkte ausrechnet, setzt man für die Berechnung des Marktgleichgewichtes die Gleichungen von Angebots- und Nachfragefunktion gleich: [math]p_N(x_{GG})=p_A(x_{GG})[/math]. [br][br]2. Wird die daraus resultierende Gleichung nach [math]x_{\left\{GG\right\}}[/math] aufgelöst, so erhält man die [b]Gleichgewichtsmenge[/b] [math]x_{GG}[/math].[br][br]3. Die Gleichgewichtsmenge kann dann in die Nachfrage- oder in die Angebotsfunktion eingesetzt werden und man erhält den [b]Gleichgewichtspreis[/b]: [math]p_{GG}=p_N(x_{GG})=p_A(x_{GG})[/math].
Gegeben sind die Nachfragefunktion [math]p_N\left(x\right)=-0,5\cdot x+6[/math] und die Angebotsfunktion [math]p_A\left(x\right)=0,2\cdot x+1,5[/math]. Dies ist das Zahlenbeispiel zu oben stehendem Bild.[br][br]1. [b]Gleichsetzen[/b]: [br][math]p_N\left(x_{GG}\right)=p_A\left(x_{GG}\right)[/math] daraus folgt [math]-0,5\cdot x_{GG}+6=0,2\cdot x_{GG}+1,5\quad\Rightarrow[/math] [br][br]2. [b]Nach[/b] [math]x_{GG}[/math] [b]auflösen[/b]: Addiere die Gleichung oben auf beiden Seiten mit [math]0,5\cdot x_{GG}[/math] und subtrahiere auf beiden Seiten [math]1,5[/math], dann folgt daraus [math]0,7\cdot x_{GG}=4,5[/math]. Teilen durch [math]0,7[/math] ergibt [math]x_{GG}\approx6,43[/math].[br][br]3. [b]Einsetzen der Gleichgewichtsmenge in z.B. die Angebotsfunktion[/b]: [math]p_{GG}=0,2\cdot6,43+1,5\approx2,79[/math][br][br]Das Marktgleichgewicht ist also [math]MGG(p_{GG}|x_{GG})=MGG(6,43|2,79)[/math][br][br][b]Mit dem folgenden Applet lässt sich die Rechnung üben:[/b][br]Bei richtigen Ergebnissen gibt es einen Punkt. Wer sich das Ergebnis zwischendurch anschaut, bekommt allerdings keinen Punkt mehr.[br][color=#980000][b]Schaffen Sie 10 Punkte:[/b][/color]

