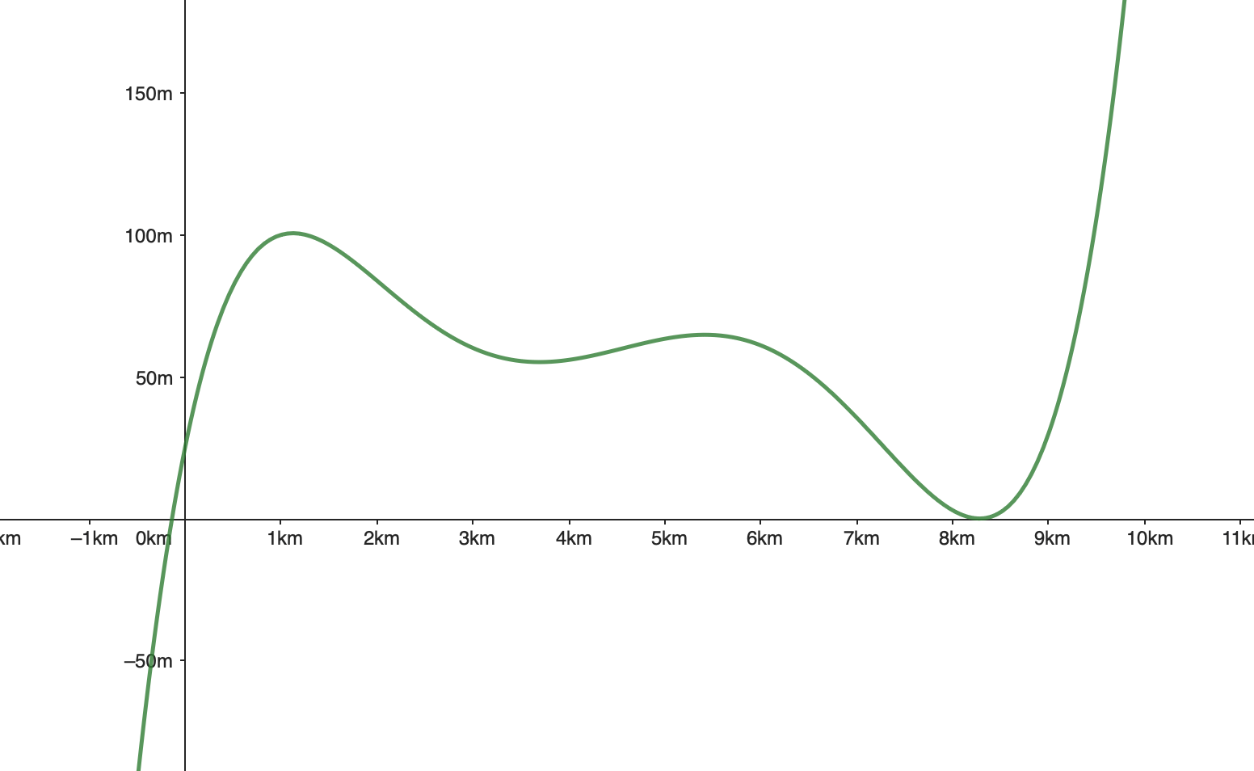
Ein 9,5 km langer Wanderweg an der Algarve führt von Cavoeiro bis zum Praia do Marinha.[br][br]Die Funktion f ordnet der Länge des zurückgelegten Weges jeweils die aktuelle Seehöhe zu.[br]f: [0,23] → R+, Weg (in km) → Seehöhe (in m)[br][br]Gerade beim Wandern oder Rad fahren interessiert dich sicher, wann es bergauf und wann es bergab geht. Mathematisch gesehen fragen wir uns dabei, ob Funktionswerte steigen (wachsen) oder fallen.[br]Wir untersuchen also die Monotonie der vorgegeben Funktion. [br]Die Aufgaben findest du unterhalb des Applets.[br][br][b][size=150][size=200]Dokumentation auf dem beigelegten Zettel![/size][/size][/b]
[size=150][b]Nutze die Ableitungsfunktion erst ab Aufgabe 3. [br][/b][br][b]Aufgabe 1) [br][/b]Beschreibe die Funktion, die dem Höhenprofil der Abbildung zugrunde liegt. Hier geht es um den realen Verlauf der Wanderung verknüpft mit dem Applet. [br][br]Zum Beispiel: f(0) ≈ 20 m: Carvoeiro liegt 20 m über dem Meer.[br][br][b]Aufgabe 2)[/b][br]Untersuche das Monotonieverhalten der Funktion. Gehe dafür den gesamten Weg ab. [br][br]Zum Beispiel:[br]In 0 ˂ x ˂ 1,2 ist f streng monoton steigend: Die ersten 1,2 km geht es bergauf.[br][/size][br]

[size=150][b]Aufgabe 3) [br][/b]a) [br]Skizziere die Ableitungsfunktion. [br][/size][size=150]Vergleiche deine Lösung mit der Ableitungsfunktion aus dem Schaubild. [br][br]b) [br]Untersuche, wie man mithilfe der Ableitungsfunktion erkennen kann, ob der Wanderer bergauf oder bergab geht. [/size]
[size=150][b]Aufgabe 4)[br][/b][b]Formuliere einen allgemeinen Satz der Monotonie[/b], der den Verlauf der Funktion und die Ableitungsfunktion verknüpft. Nutze die konkreten Formulierungen aus 3b) für eine [b]allgemeine[/b] Formulierung. [br][br][/size]Solltest du nicht weiterkommen, dann habe ich Formulierungshilfen für dich!