目标函数:[br][br] [math]min\frac{1}{2}\sum^n_{i=1}\sum^n_{j=1}a_ia_jy_iy_j\left[\varnothing\left(x_j\right)\right]-\sum^n_{i=1}a_i[/math] ……目标函数[br][br] 约束条件: [math]\sum a_iy_i=0[/math] ……约束条件 1[br][br] [math]a_i\ge0[/math] ……约束条件 2[br][br] 在以上极限求解公式中,[math]\varnothing\left(x_i\right)\cdot\varnothing\left(x_j\right)[/math]为两个向量的内积。向量内积(inner product),又称数量积(scalar product)、点积(dot product)。它是一种矢量运算,但其结果为某一数值,并非向量。简单来讲,设向量 [math]A=(a_1a_2...a_n),B=\left(b_1b_2...b_n\right)[/math] ,则向量 A 和 B 的内积表示为;[br][br] [math]A\cdot B=a_1\times b_1+a_2\times b_2+...+a_n\times b_n[/math][br][br] 在约束条件中,支持向量点的 [math]a>0[/math],而非支持向量点[math]a=0[/math] 。
【实例讲解(二维点)】[br][br] 假设有三个点,正例点为[math]x_1(3,3)[/math] , [math]x_2(4,3)[/math] ,负例点为 [math]x_3(1,1)[/math] ,假设这三个点是可能的支[br]持向量,我们希望通过线性规划的求解方式找到正例点与负例点之间的超平面。而要找到超平面,首先要定位支持向量点,支持向量点是分类的临界点,也是正确定义超平面的关键点。[br][br] 根据以上三个点的特性可知, [math]y_1=y_2=1[/math],[math]y_3=-1[/math],由此可定义求解公式为[br] [br] [math]min\frac{1}{2}\sum^3_{i=1}\sum^3_{j=1}a_ia_jy_iy_j\left[\varnothing\left(x_i\right)\cdot\varnothing\left(x_j\right)\right]-\sum^3_{i=1}a_i[/math] ……目标函数[br][br] 约束条件:[br][br] [math]a_1+a_2-a_3=0[/math] ……约束条件 1[br][br] [math]a_1,a_2,a_3\ge0[/math] ……约束条件 2[br][br] 将所有数据代入极限求解公式,可得目标函数为[br][br] [math]min\frac{1}{2}\left(18a_1^2+25a^2_2+2a^2_3+42a_1a_2-12a_1a_3-14a_2a_3\right)-a_1-a_2-a_3[/math] <1>[br][br] 因为约束条件为 [math]a_1+a_2=a_3[/math],代入化简可得 [math]4a^2_1+\frac{13}{2}a^2_2+10a_1a_2-2a_1-2a_2[/math],分别对 [math]a_1[/math]和 [math]a_2[/math]求偏导,让偏导等于 0,可得出解为: [math]a_1=1.5[/math] , [math]a_2=-1[/math]。[br][br] 由于[math]a_2=-1<0[/math],不满足约束条件 2,可以由此基本得出判断, [math]a_2[/math] 可能不是支持向量点,因为支持向量点一定要满足约束条件 1、2,即至少要满足大于等于 0 的条件。[br][br] 基于以上基本判断,可以假设支持向量点为[math]x_1[/math] 和 [math]x_3[/math],在这个假设前提下, [math]a_2=0[/math]( [math]x_2[/math] 为非支持向量点)。根据式(2-8-1),目标函数及约束条件为:[br][br] [math][/math]目标函数:[math]min\frac{1}{2}\left(18a^2_1+2a^2_31-12a_1a_3\right)-a_1-a_3[/math] <2>[br][br][br] 约束条件:[math]a_1=a_3,a_1,a_3\ge0,a_2=0[/math]
由于 [math]a_1=a_3[/math],代入式<2>,化简可得: [math]4a^2_1-2a_1[/math],同样对 [math]a_1[/math] 求导,令其等于 0,则极值点的 [math]a_1[/math]=0.25 ,可得 [math]a_2[/math]=0 ,[math]a_3=0.25[/math] 。可以看出,这一组 [math]a[/math] 值符合约束条件,验证了此前所设定的 [math]x_1[/math] 和 [math]x_3[/math]为支持向量点的假设是正确的。[br][br] 至此,支持向量点为 [math]x_1[/math] 、 [math]x_3[/math],所对应的 [math]a[/math]值为[0.25,0.25]。接下来,需要求解这个超平面的 [math]w[/math]值和 [math]b[/math]值。[br][br] 根据超平面 [math]w[/math]值求解算式:[math]w=\sum^n_{i=1}a_iy_i\varnothing\left(x_n\right)[/math],代入数值, [math]w=\frac{1}{4}\times1\times\left(3,3\right)+\frac{1}{4}\times\left(-1\right)\times\left(-1\right)=\left(0.5,0.5\right)[/math] 。[br][br] 根据超平面 b 值求解算式:[math]b=y_i-w^T\varnothing\left(x_i\right)[/math],这里代入 [math]x_1[/math] 的值, [math]b=1-\binom{0.5}{0.5}\cdot\left(33\right)=1-3=-2[/math]。[br][br] 所求解的超平面方程为 [math]0.5x_1+0.5x_2-2=0[/math],如图 2-8-6 所示。
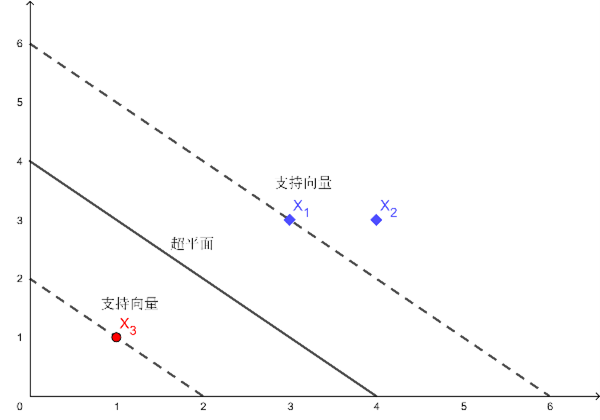
[size=100][center] 图 2-8-6 示例二维点超平面[/center][/size]

