[size=150][b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][/b][/size][b]光速が絶対不動の最高速度である[/b]ことを基準にして、[br][b]絶対時空間がないので慣性系（等速運動）の物理法則が静止した状態と同じに成り立つ[/b]という前提から[br]どんな結論が出るだろうか？[br][br]「光速に近いロケットで旅して地球にもどると、自分は若いままで周りが年老いる」[br]「光速に近いロケットは長さが縮む」[br]という話はよく聞く。[br][br]それはどういうことだろうか？[br][br]今回はそれらを取り上げてみよう。

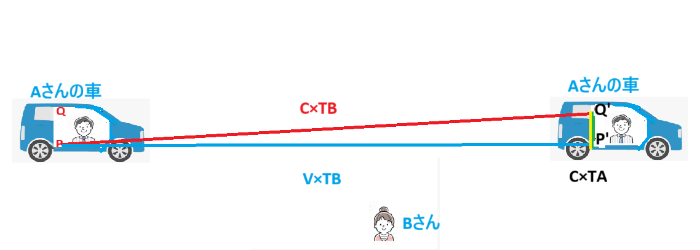
[b][size=150]＜斜辺とくらべてわかること＞[/size][/b][br][br]車の中で光線が床の点Pからまっすぐ発射されて天井の点Qに達するまでの時間を考えよう。[br]それを観測する人は2人いる。[br]車中のAさんと、[br]車外の道路にいるBさんだ。

この時間はAさんにとって[b]TA秒[/b]としよう。[br]進むのは光だから、光速を[b]秒速ｃ㎞[/b]とすと、[br][b][size=200]たて＝ｃ×TA[/size][/b][br]このようすをBさんか見たらどうなるかな。車は一定の[b]秒速ｖ㎞[/b]で進むとしよう。[br]先端点Cは移動後のQ'までまっすく進む。この時間はBさんが測定するから[b]TB秒[/b]とする。[br]進むのは光だから、[br][b][size=200]斜辺＝ｃ×TB[/size][/b][br]床のP点は車といっしょに真横にまっすぐ進む。[br]進むのは車だから、[br][b][size=200]横＝ｖ×TB[/size][/b][br][br]ここで、斜辺に対する、他の辺の比を考えると面白いことがわかる。[br]・よこ/斜辺は、両方ともBさんが見た長さだから、時間TBが共通だ。[br]時間が共通のときは、道のりは速さに比例するので、よこ/斜辺＝v/cになる。[br]この図では、Aさんの車は光速ｃに近いスピードｖで進んでいることになるね。[br]数式だけでやると、[br][size=200][b][color=#0000ff]よこ/斜辺＝vTB/cTB=v/c[/color][/b][br][/size][br]・たて/斜辺は、両方とも光が進んだ軌跡だ。[br]たてはAさんからみた光の道筋、斜辺はBさんからみたもの。[br]進むものが光である以上、光はどの慣性系でも不変の速さだから、同じ時間なら同じだけ進む。[br]しかし、光がすすんだ道のりがちがっている。[br][b][color=#0000ff][size=150]光速一定を基準にすると、道のりが違うのは経過時間がちがうという結論になる[/size][/color][/b]。[br]同じ時間が経過したはずなのに、BさんにはTB秒、AさんにはTA秒と区別するしかないのだ。[br][b][color=#0000ff][size=200]たて/斜辺＝cTA/cTB=TA/TB[/size][/color][/b]

[b][size=150]＜ピタゴラスの定理で２種の比とつなごう＞[/size][/b][br][br]さっきは２つの比[br]よこ/斜辺＝v/c[br]たて/斜辺＝TA/TB[br]までわかったね。[br]いよいよ、この２つをつないでみよう。[br]つなぐキューピットはピタゴラスの定理だ。[br]ピタゴラスの定理は、辺の長さの定理でもあり、[br]辺の比の定理ともいえる。[br]だから、斜辺をカンタンのために１の長さにしてしまおう。[br]すると、[br][b][size=200]斜辺＝１、よこ＝v/c、たて＝TA/TB[br][/size][/b]となる。[br][br]ここで、ピタゴラスの定理にあてはめよう。[br][b][size=150][size=200][color=#0000ff]1=(TA/TB)[sup]2[/sup]+(v/c)[sup]2[/sup][br]TA/TB=√(1- (v/c)[sup]2[/sup])[br][/color][/size][/size][/b]となるね。[br][br]・前回、[color=#0000ff][b][size=150]斜辺を１残りの辺をu,vとしたときに、u/c=√(1-(v/c)[sup]2[/sup])[/size][/b][/color]となることがわかった。[br]この事実に、ピタゴラス数を使って、どのくらい時間の進みが遅くなるかがカンタンにわかるはずだ。[br]ピタゴラス数３：４：５を使う。[br][b]車が光速の4/5倍の速さで進むと、かかる時間が3/5にちぢむ。[/b]たとえば、[br]地上の50年たってもどると、ロケットの中では30年時間がたっていることになる。[br]ピタゴラス数５：１２：１３を使う。[br][b]光速の12/13倍の速さで進むと、計算上5/13しか老けないことなる。[/b]

[b][size=150]＜時間が縮むと長さも縮む？＞[br][/size][/b]光速に近い速さｖで進むと、進んでいるAさんの時間TAは[br]外から見ているBさんの時間TBに対して、時間がTA/TB＝√(1-(v/c)[sup]2[/sup]倍に縮むことがわかった。[br]これは、数式上は難しそうに見えるけど、[br]直角三角形の斜辺を１としたとき、TA/TBがよこ、v/cがたてなので、[br]たての長さからよこの長さを出す計算をしているだけだとわかったね。[br][br]では、1秒で進む距離より長い物を1秒で通過できる話しに入ろう。[br]秒速ｖの車が長さがｖより長いｗの長さトンネルを1秒で通過できる[br]という手品みたいな理由をさぐろう。[br]さっきと同じく、[br]車にはAさんがのり、[br]外でBさんが見ているとする。[br]Bさんは、「[b][color=#0000ff]秒速ｖで、ｖより長いトンネルを１秒で通過するなんて、無理でしょ！[/color][/b]」[br]と思って観察している。[br]Aさんは、「[b][color=#0000ff]ｖは光速に近いから、トンネルが縮んでくれるよ！[/color][/b]」[br]と思って運転する。

Aさんの車の速さｖはBさんから見てもAさんからも変わらないね。[br]Aさんからすると、トンネルが速さｖで進んでくるのが見えるでしょう。[br]車の長さはトンネルの長さからみて無視できるものとしよう。[br]AさんのTAの時間でトンネルを通過したら長さは[b]ｖTA[/b]になる。これを[b]LA[/b]としよう。[br]BさんのTBの時間でトンネルを通過したら長さは[b]ｖTB[/b]になる。これを[b]LB[/b]としよう。[br][br]ｖが共通だから、比は等しい。[b][size=200]TA/TB=LA/LB[/size][/b]。[br][br]どうでしょうか。[br]同じトンネルなのに、光速に近いスピードで進むAさんからすると、[br][b][color=#0000ff][size=150]トンネルの長さは時間のちぢむ比率と同じ比率で縮む[/size][/color][/b]ことになる。[br][br]たとえば、ピタゴラス数の３：４：５から、[b]v/c=4/5なら、TA/TB=3/5=LA/LB[/b] 。[br]だから、[b]v=秒速30万㎞の4/5=秒速24万㎞の車[/b]なら、[br][b]長さが40万㎞のトンネルが50×3/5=24万㎞に縮む[/b]ことになるね。[br]つまり、Bさんから見て40万㎞の長さのトンネルを[br]Aさんの車は秒速24万㎞で[u]Aさんの時間で１秒[/u]で通過できることになる。[br][br]これは、Aさんの車の通る時空が縮んだだけで、Bさんの世界は通常と変わっていない。[br]40万kmのトンネルを秒速24万kmの車が通過するには、40÷24=5/3＝1.6666...(秒）かかっている。[br]だから、Bさんに言わせれば「ほーら、1秒じゃあ無理でしょ」となる。[br]でも、Bさんの世界の1.666...＝5/3秒は車のスピードのおかげで[br]Aさんの世界では5/3×3/5=1秒になるということだね。[br]だから、Aさんの世界では秒速24万㎞で1秒で通過したからトンネルは24万kmだということだ。[br]どちらも、言っていることは正しいことなる。