LINGKARAN

Atana Sa'adah, Mar 11, 2025

• Lingkaran • Unsur-unsur lingkaran • Panjang busur • Luas juring • Hubungan sudut pusat dengan sudut keliling • Garis singgung persekutuan dalam dua lingkaran • Garis singgung persekutuan luar dua lingkaran

Table of Contents

  1. Unsur Unsur Lingkaran
    1. UNSUR-UNSUR LINGKARAN
  2. Panjang Busur
    1. Panjang Busur Lingkaran
  3. Luas Juring
    1. Panjang Busur dan Luas Juring
  4. Hubungan Sudut Pusat dengan Sudut Keliling
    1. Sudut Pusat dan Sudut Keliling Lingkaran
  5. Garis Singgung Persekutuan Dalam Dua Lingkaran
    1. Garis Singgung Lingkaran
  6. Garis Singgung Persekutuan Luar Dua Lingkaran
    1. Garis Singgung Persekutuan Luar Dua Lingkaran #1
    2. Garis Singgung Persekutuan Luar

1.

Unsur Unsur Lingkaran

  • 1. UNSUR-UNSUR LINGKARAN

1.1.

UNSUR-UNSUR LINGKARAN

[justify][size=100]Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama dengan satu titik tertentu.Unsur-unsur lingkaran terdiri dari:[br]1. Titik Pusat (P): Titik yang menjadi pusat lingkaran yang terletak tepat di tengah lingkaran[br]2. Jari-jari (r): jarak antara pusat lingkaran dengan titik pada lingkaran[br]3. Diameter (d): garis yang menghubungkan dua titik pada lingkaran melalui titik pusat[br]4. Busur Lingkaran: garis berbentuk melengkung pada tepian lingkaran[br]5. Tali Busur: garis yang menghubungkan dua titik pada lingkaran[br]6. Juring Lingkaran: daerah yang dibatasi oleh busur dan dua jari-jari lingkaran[br]7. Tembereng: daerah yang dibatasi oleh busur dan tali busur[br]8. Apotema: garis yang menghubungkan titik pusat dengan tali busur (tegak lurus dengan tali busur)[br][br]Untuk lebih jelasnya, mari perhatikan gambar berikut.[/size][/justify]
Mengenal Unsur-unsur Lingkaran
Dapat disimpulkan unsur-unsur lingkaran apa saja?
– Untung Trisna S., Atana Sa'adah, I'anatul Hidayah

2.

Panjang Busur

  • 1. Panjang Busur Lingkaran

2.1.

Panjang Busur Lingkaran

Tujuan Pembelajaran
1. Siswa mampu menentukan panjang busur lingkaran[br]2. Siswa mampu menuliskan kembali rumus-rumus yang berkaitan dengan panjang busur lingkaran[br]3. Siswa mampu menggunakan rumus-rumus yang berkaitan dengan panjang busur lingkaran pada soal[br]4. siswa mampu menguraikan permasalahan yang berkaitan dengan panjang busur
Keliling Lingkaran
Lalu, apa kaitannya antara panjang busur dengan keliling lingkaran?[br]Simak simulasi GeoGebra berikut ini!
Busur Lingkaran
Dari apa yang sudah kita pelajarai diatas, dapat disimpulkan bahwa busur adalah garis lengkung yang merupakan bagian dari keliling lingkaran.
Lalu, untuk mencari panjang busur bagaimana caranya?
Panjang Busur Lingkaran
Yuk kita coba!
[b][size=100]Perhatikan lingkaran diatas, jika <AOB = ∝. Tentukan rumus untuk mencari panjang busur AB![/size][/b]
Kerjakan soal berikut ini dengan benar!
Perhatikan gambar lingkaran diatas, jika panjang busur AB= 33 cm. Berapakah panjang busur CD?
Dari pembelajaran hari ini dapat disimpulkan bahwa untuk mencari panjang busur lingkaran, bisa menggunakan rumus berikut:
– Komang Putra Astrawan, Zona Asha Tigara, Atana Sa'adah, Gladissela

3.

Luas Juring

  • 1. Panjang Busur dan Luas Juring

3.1.

Panjang Busur dan Luas Juring

– Atana Sa'adah, Zona Asha Tigara

4.

Hubungan Sudut Pusat dengan Sudut Keliling

  • 1. Sudut Pusat dan Sudut Keliling Lingkaran

4.1.

Sudut Pusat dan Sudut Keliling Lingkaran

Dengan menggunakan Lembar Kerja ini kamu akan memahami hubungan sudut pusat dan sudut keliling lingkaran.[br]Selamat Bereksplorasi
Berapa besar sudut keliling jika sudut pusatnya [math]60^0[/math]?
Bagaimana hubungan sudut keliling yang mengahadap ke busur yang sama?
Bagaimana hubungan sudut pusat dan sudut keliling yang menghadap ke busur yang sama?
– hermawan, Denny Pritianto, Atana Sa'adah, I Putu Eka Wahyu Juliasta

5.

Garis Singgung Persekutuan Dalam Dua Lingkaran

  • 1. Garis Singgung Lingkaran

5.1.

Garis Singgung Lingkaran

Tujuan Lembar Kerja Siswa
1. Siswa dapat memahami konsep garis singgung lingkaran dengan baik.[br]2. Siswa dapat membedakan garis singgung persekutuan dalam dan luar dua lingkaran dengan jelas.[br]3. Siswa dapat mencari garis persekutuan dalam dan luar dua lingkaran secara efektif.
Konsep Garis Singgung Lingkaran
1. Apa definisi garis singgung lingkaran?
2. Di bawah ini, manakah yang termasuk sifat garis singgung lingkaran?
Gunakan applet untuk menjawab pertanyaan no. 3-5!
3. Berapa panjang garis singgung QR, jika panjang jari-jari lingkaran P adalah 6 cm dan panjang PR adalah 10 cm? ... cm
4. Berapa panjang garis singgung QR, jika jari-jari lingkaran P adalah 5 cm dan panjang PR adalah 13 cm? ... cm
5. Berapa panjang garis singgung QR, jika jari-jari lingkaran P adalah 3 cm dan panjang PR adalah 5 cm? ... cm
Konsep Garis Singgung Persekutuan Dalam dan Luar Dua Lingkaran (GSPD dan GSPL)
6. Pasangan mana GSPD dan GSPL yang benar secara berurutan?
Gunakan applet untuk menjawab pertanyaan no. 7-8!
7. Panjang jari-jari lingkaran A dan B berturut-turut adalah 10 cm dan 5 cm. Jarak kedua pusat lingkaran adalah 25 cm. Berapa panjang garis singgung persekutuan dalam kedua lingkaran tersebut? ... cm
8. Dua buah lingkaran memiliki jari-jari masing-masing 7 cm dan 2 cm. Jarak antara pusat kedua lingkaran adalah 15 cm. Berapakah panjang garis singgung persekutuan dalam kedua lingkaran tersebut? ... cm
Gunakan applet untuk menjawab pertanyaan no. 9-10!
9. Dua lingkaran dengan jari-jari masing-masing 2 cm dan 11 cm memiliki panjang antara titik pusatnya sebesar 15 cm. Berapa panjang garis singgung luar lingkaran tersebut? ... cm
10. Dua lingkaran dengan jari-jari masing-masing 10 cm dan 3 cm memiliki panjang antara titik pusatnya sebesar 25 cm. Berapa panjang garis singgung luar lingkaran tersebut?... cm
– Elva Kurnia Putri, Hani'atun Nurul Himah, Atana Sa'adah, Kartika Rahmania Putri

6.

Garis Singgung Persekutuan Luar Dua Lingkaran

  • 1. Garis Singgung Persekutuan Luar Dua Lingkaran #1
  • 2. Garis Singgung Persekutuan Luar

6.1.

Garis Singgung Persekutuan Luar Dua Lingkaran #1

Pertemuan 9. Garis Singgung Persekutuan Luar Dua Lingkaran
[b]Capaian Pembelajaran[br][/b]Di akhir fase F, peserta didik dapat menerapkan teorema tentang lingkaran, dan menentukan panjang busur dan luas juring lingkaran untuk menyelesaikan masalah (termasuk menentukan lokasi posisi pada permukaan bumi dan jarak antara dua tempat di bumi).[br][br][b]Tujuan Pembelajaran:[br][/b]Setelah kegiatan pembelajaran ini selesai ini diharapkan peserta didik dapat:[br]1.  Menentukan panjang garis singgung persekutuan luar dua lingkaran[br]2. Menyelesaikan permasalahan yang berkaitan dengan garis singgung persekutuan luar dua lingkaran.
Kegiatan 1
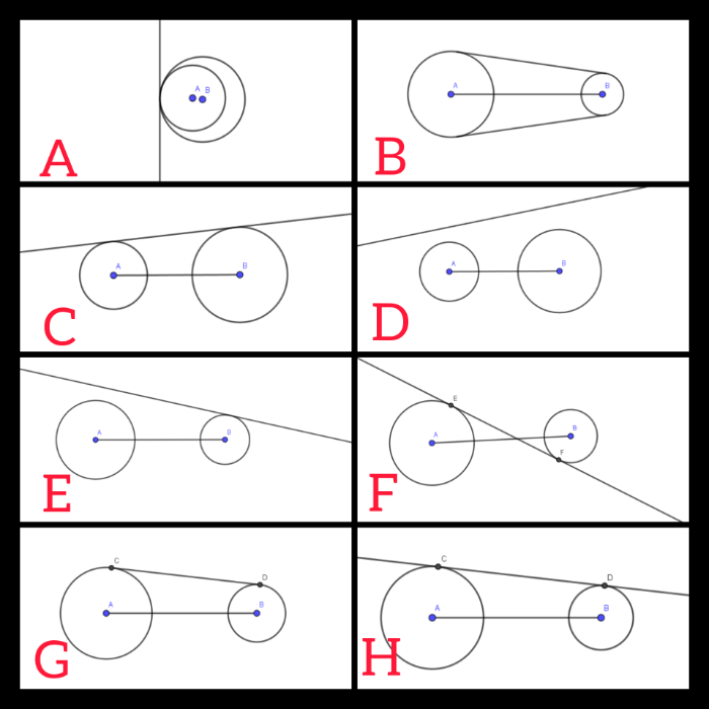
Jawablah pertanyaan berikut:[br]1. Gambar manakah yang merupakan gambar garis singgung persekutuan luar dua lingkaran?[br]2. Definisikan GSPL dua lingkaran dengan menggunakan bahasa kalian sendiri
Kegiatan 2.
Petunjuk penggunaan :[br]1. Centang kotak mulai dari kiri ke kanan[br]2. Perhatikan unsur-unsur apa saja yang dapat digunakan untuk menentukan GSPL dua lingkaran
Jawablah Pertanyaan Berikut
[list=1][*]Garis apakah yang menunjukkan GSPL dua lingkaran dalam applet diatas?[/*][*]Garis apakah yang sejajar dengan GSPL dua lingkaran tersebut?[/*][*]Perhatikan segitiga siku-siku AGB. Jika segitiga siku-siku AGB siku-siku di G, maka bagaimanakah cara menghitung GB?[/*][*]Jadi kesimpulannya bagaimanakah cara menghitung GSPL dua lingkaran?[/*][/list]
Jawablah Pertanyaan Berikut:
[list=1][*]Jika R[sub]A[/sub] > R[sub]B[/sub], adakah garis singgung persekutuan luarnya? Bagaimana cara mengukur panjang GSPL nya?[/*][*]Jika R[sub]A[/sub] < R[sub]B[/sub], adakah garis singgung persekutuan luarnya? Bagaimana cara mengukur panjang GSPL nya?[/*][*]Jika R[sub]A[/sub] = R[sub]B[/sub], adakah garis singgung persekutuan luarnya? Bagaimana cara mengukur panjang GSPL nya?[/*][*]Jika titik pusat lingkaran A berada diluar lingkaran B, adakah garis singgung persekutuan luarnya? Bagaimana cara mengukur panjang GSPL nya?[/*][*]Jika titik pusat lingkaran A dan lingkaran B berhimpitan, adakah garis singgung persekutuan luarnya? Bagaimana cara mengukur panjang GSPL nya?[/*][/list]
Kerjakan Soal Berikut.
1. Diketahui dua lingkaran dengan pusat P dan Q, jarak PQ = 26 cm, panjang jari-jari lingkaran masing-masing 12 cm dan 2 cm. Panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah. . .[br]
2. Jari-jari lingkaran yang berpusat di A sama dengan 2 kali jari-jari lingkaran yang berpusat di B. Jika panjang garis singgung persekutuan luar kedua lingkaran itu 36 cm dan jarak kedua pusatnya 39 cm, maka panjang jari-jari lingkaran A adalah...
3. Diketahui dua lingkaran berjari-jari masing-masing 12 cm dan 5 cm. Jika panjang garis singgung persekutuan luarnya 24 cm, maka jarak titik pusat kedua lingkaran tersebut adalah...
4. Perhatikan gambar berikut.
Jika luas daerah yang diarsir adalah 165 [math]cm^2[/math], maka panjang AB adalah...
5. Perhatikan gambar di bawah ini.
Enam pipa paralon dengan penampang seperti gambar berjari-jari 21 cm saling bersinggungan luar. Panjang tali minimum yang dapat digunakan untuk mengikat keenam pipa paralon tersebut adalah...
Kesan dan Saran
Bagaimanakah kegiatan pembelajaran hari ini? Berikan kesan dan saran kalian dalam kolom di bawah ini.
– Atana Sa'adah, bebydnoverianto01

6.2.

–

Information