A research on Generalization and Applications of Cycloid

이상민, Apr 13, 2015

Table of Contents

  1. Introduction
    1. Beginning
    2. Why Cycloid?
    3. Brachistochrone Curve and Tautochrone Curve
  2. Cycloid
    1. Cycloid
    2. Parametric Equations of Cycloid
  3. Hypocycloid and Epicycloid
    1. Hypocycloid
    2. Parametric Equations of Hypocycloid
    3. Epicycloid
    4. Parametric Equations of Epicycloid
  4. Hypotrochoid and Epitrochoid
    1. Hypotrochoid
    2. Parametric Equations of Hypotrochoid
    3. Epitrochoid
    4. Parametric Equations of Epitrochoid
  5. Generalization
    1. Generalization #1
    2. Generalization #2
  6. Folding Door of Bus
    1. Application #1
  7. Wankel Rotary Engine
    1. Application #2
  8. Modeling the Solar System
    1. Visualization with GeoGebra
  9. Future Plans & References
    1. Future Plans
    2. References
    3. Ending

1.

Introduction

  • 1. Beginning
  • 2. Why Cycloid?
  • 3. Brachistochrone Curve and Tautochrone Curve

1.1.

Beginning

Self Introduction
[size=100][b][size=150]Hi, I am [color=#ff7700]Sang Min Lee[/color] from [color=#ff7700]Korea Science Academy of KAIST[/color].[br]I am [color=#ff7700]high-school student and GeoGebra beginner[/color].[br]My instructor is [color=#ff7700]Young Cheol Jeon[/color] and he is mathematics teacher in Korea Science [/size][size=150]Academy.[/size][size=150][font=Trebuchet MS][br]From now on, I am going to talk about my research on [color=#ff7700]Generalization and Applications of Cycloid Curve with the use of GeoGebra[/color].[/font][/size][/b][/size]
Location of South Korea
Korea Science Academy of KAIST
– 이상민

1.2.

–

1.3.

–

2.

Cycloid

  • 1. Cycloid
  • 2. Parametric Equations of Cycloid

2.1.

Cycloid

Cycloid Modeling by GeoGebra
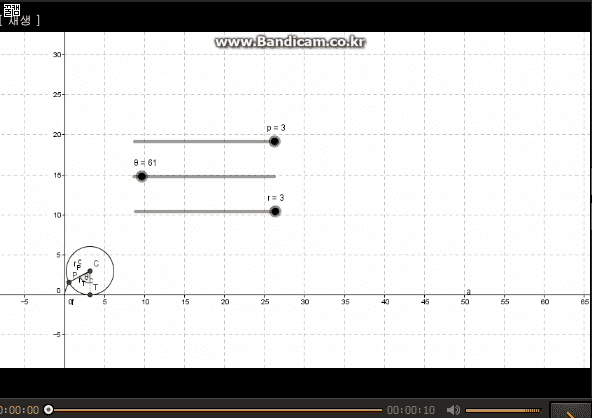
Definition of Cycloid
[b][size=150][color=#ff7700]Cycloid[/color] is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line without slippage.[/size][/b]
– 이상민

2.2.

–

3.

Hypocycloid and Epicycloid

  • 1. Hypocycloid
  • 2. Parametric Equations of Hypocycloid
  • 3. Epicycloid
  • 4. Parametric Equations of Epicycloid

3.1.

Hypocycloid

Hypocycloid Modeling by GeoGebra
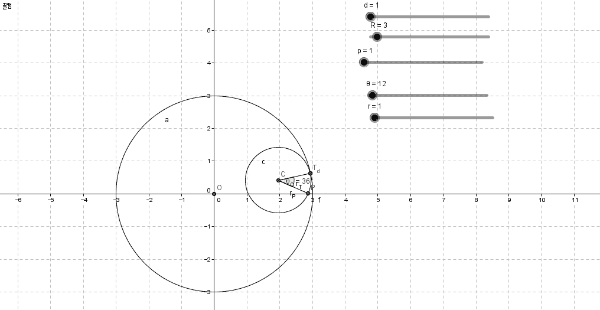
Definition of Hypocycloid
[font=Trebuchet MS][size=150][b][color=#ff7700]Hypocycloid[/color] is the curve generated by the trace of a fixed point on a small circle that rolls within a larger circle.[br]It is comparable to the cycloid but instead of the circle rolling along a line, it rolls within a circle.[/b][/size][/font]
– 이상민

3.2.

–

3.3.

–

3.4.

–

4.

Hypotrochoid and Epitrochoid

  • 1. Hypotrochoid
  • 2. Parametric Equations of Hypotrochoid
  • 3. Epitrochoid
  • 4. Parametric Equations of Epitrochoid

4.1.

Hypotrochoid

Hypotrochoid Modeling by GeoGebra
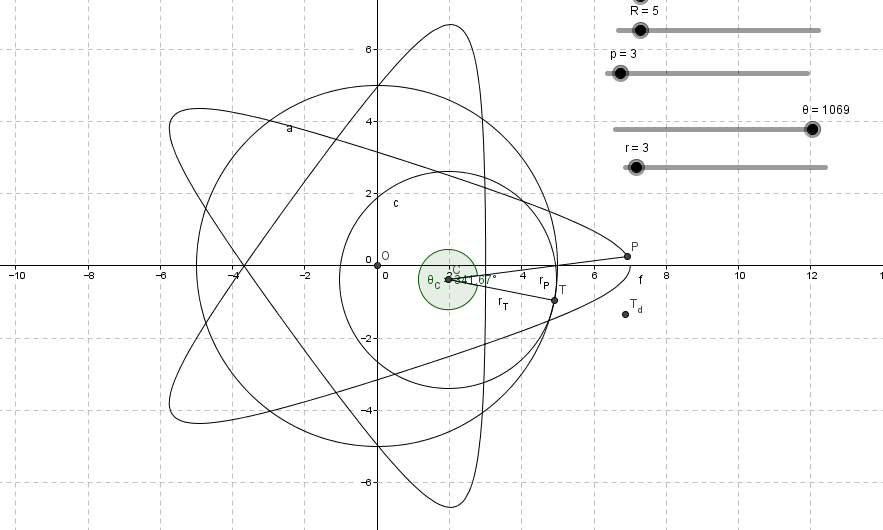
Definition of Hypotrochoid
[font=Trebuchet MS][b][size=150][color=#ff7700]Hypotrochoid[/color] is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle.[/size][/b][/font]
– 이상민

4.2.

–

4.3.

–

4.4.

–

5.

Generalization

  • 1. Generalization #1
  • 2. Generalization #2

5.1.

Generalization #1

Generalization of Hypocycloid
[size=150][font=Trebuchet MS][b]At first, we tried to find the parametric equations with the similar way of previous one.[br]However, it wasn't easy to figure out. Therefore, I tried with a[color=#ff7700] method using vectors[/color].[br]Since this curve is continuous curve, we set a tiny angle moved state and find the coordinate of each vector, add them all.[/b][/font][/size]
– 이상민

5.2.

–

6.

Folding Door of Bus

  • 1. Application #1

6.1.

Application #1

[font=Trebuchet MS][size=150][b]The first application is folding door of bus.[br][br][color=#ff7700]Mechanism of folding door is until 45 degrees, it follows the envelope curve.[br]After then, it follows the rim of a circle.[br][/color][br]The proof of parametric equation of it is written below.[/b][/size][/font]
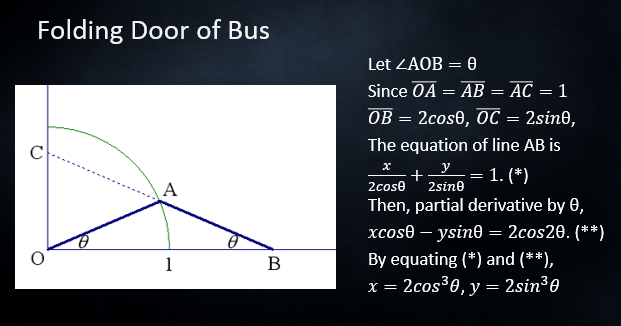
Relation with my topic
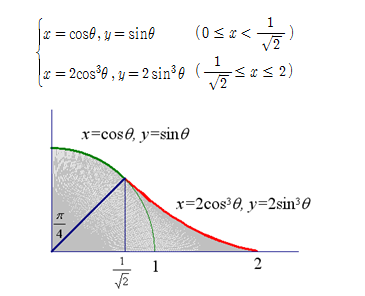
[font=Trebuchet MS][b][color=#ff7700][size=150]This parametric equation is same with the Astroid[br](particular type of hypocycloid)[/size][/color][/b][/font]
– 이상민

7.

Wankel Rotary Engine

  • 1. Application #2

7.1.

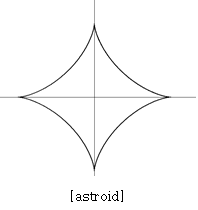
Application #2

[font=Trebuchet MS][b][size=150]The second application is [color=#ff7700]Wankel Rotary Engine[/color].[/size][/b][/font]
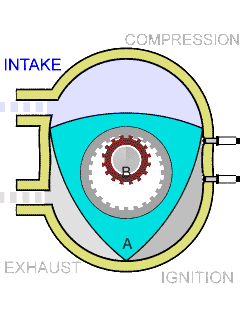
[font=Trebuchet MS][b][size=150]Above one is the gif image of [color=#ff7700]Wankel Rotary Engine[/color].[br]As you can see, gas comes in and compression follows. Thus, piston is able to get force.[br]After the firing process, exhaustion and emission occurs.[/size][/b][/font]
In the calculus book
Relation with my topic
[font=Trebuchet MS][b][color=#ff7700][size=150]As the description in calculus, is is applied from epitrochoid.[/size][/color][/b][/font]
Equilateral Triangle
– 이상민

8.

Modeling the Solar System

  • 1. Visualization with GeoGebra

8.1.

Visualization with GeoGebra

– 이상민

9.

Future Plans & References

  • 1. Future Plans
  • 2. References
  • 3. Ending

9.1.

Future Plans

Future Plans
1. Figure out the parametric equations of n-th generalized cycloid curve[br][br]2. Visualize the precise solar system with the use of GeoGebra
– 이상민

9.2.

–

9.3.

–

Information