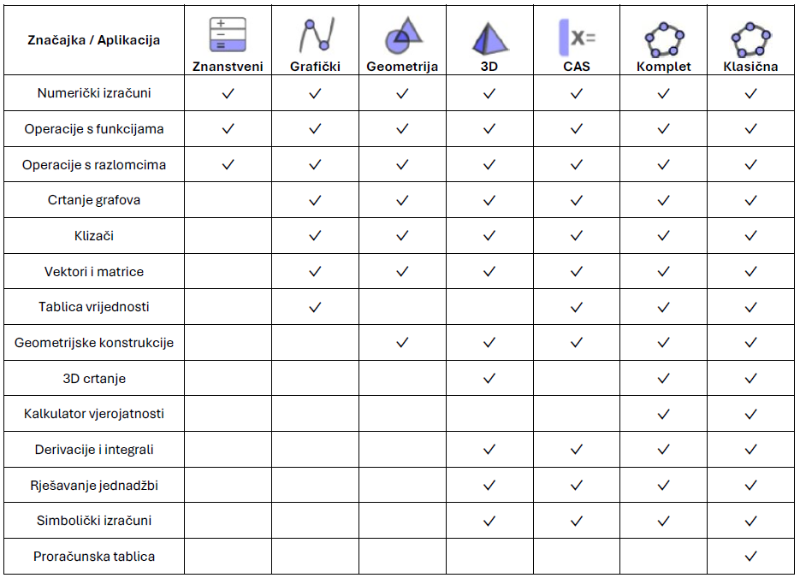
Usporedba GeoGebrinih aplikacija
S našim novim GeoGebrinim aplikacijama možete istraživati i učiti o funkcijama, geometriji, algebri, statistici i 3D na nov i interaktivan način.[br][br][list][*][url=http://www.geogebra.org/scientific]Znanstveni kalkulator[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafički kalkulator[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometrija[/url][br][/*][*][url=https://www.geogebra.org/calculator]Komplet kalkulatora[/url][/*][*][url=https://www.geogebra.org/cas]CAS Kalkulator[/url][br][/*][*][url=https://www.geogebra.org/3d]3D Kalkulator[/url][/*][*][url=https://www.geogebra.org/classic]Klasična GeoGebra[/url][/*][/list]Prava aplikacija za Vas je ona koja koristi potrebama Vas i Vaših učenika i, ako se koristi u toku ispita, zadovoljava pravnu regulativu države. Sljedeća tablica daje pregled koje su značajke dostupne u pojedinoj aplikaciji.

GeoGebra na ispitu
Čvrsto vjerujemo da će učenici profitirati od od korištenja točno one GeoGebrine aplikacie koju koriste u učionici, kod kuće, i tijekom ispita. Na taj će način dobiti najviše iskustva u radu s aplikacijom te će stoga na najbolji mogući način iskoristiti tehnologiju na pravi način u svim situacijama. Zbog toga smo izradili [url=https://www.geogebra.org/m/nauqds9v]ispitni način rada[/url] koji smo dodali u svaku našu aplikaciju. Ispitni način zaključava uređaj kako učenici ne bi mogli komunicirati s nekim ili koristiti neke druge aplikacije tijekom ispita. Ovaj je način već isproban u školama i odobren od strane nekoliko ministarstava nadležnih za obrazovanje. Pročitajte više o tome u priručniku [url=https://www.geogebra.org/m/nauqds9v]GeoGebra na ispitu[/url].[br][br]
Sjecište grafova funkcija
Zadatak
Nacrtajte linearnu funkciju s klizačima i odredite njeno sjecište s kvadratnom funkcijom. [br][br]Istražite konstrukciju i naučite kako crtati funkciju s parametrima, te kako odrediti sjecište dviju funkcija s [i][url=https://www.geogebra.org/graphing]Grafičkim kalkulatorom[/url][/i]. Zatim to pokušajte sami, slijedeći upute u nastavku.[br]
Istražite konstrukciju...
Upute
[table][tr][td]1.[/td][td][/td][td]Nacrtajte linearnu funkciju unosom[math]f(x)=a\cdot x+b[/math] u [i]Traku za unos[/i]. Klizači za varijable a i b će biti automatski kreirani.[/td][/tr][tr][td]2.[/td][td][/td][td]Omogućite [i]Vidljivost [/i]uz pomoć oznake (kruga) ispred klizača kako bi klizač bio vidljiv u [i]Grafičkom prikazu.[/i][br][/td][/tr][tr][td]3.[/td][td][/td][td]Mijenjajte vrijednosti klizača [i]a [/i]i [i]b [/i]i istražite kako to utječe na promijenu grafa [i]f(x).[/i][br][/td][/tr][tr][td]4.[/td][td][/td][td]Nacrtajte kvadratnu funkciju tako što ćete upisati [math]g\left(x\right)=x^2[/math] u [i]Traku za unos[/i][i].[/i][/td][/tr][tr][td]5.[/td][td][/td][td]Koristite naredbu [math]Sjecište\left(f,g\right)[/math] kako biste odredili sjecišta funkcija [i]f(x) [/i]i [i]g(x). [/i]Točke presjeka [i]A [/i]i [i]B [/i]će se pojaviti u [i][i]Grafičkom prikazu[/i][/i], dok će se koordinate tih točaka pojaviti u [i]Algebarskom prikazu.[/i][/td][/tr][tr][td][/td][td][icon]/images/ggb/toolbar/mode_intersect.png[/icon][/td][td][b]Napomena:[/b] Možete koristiti i alat [i]Sjecište [/i]iz [i]Alatne trake, [/i]označite funkcije čije sjecište želite odrediti.[/td][/tr][tr][td]6.[/td][td][/td][td]Pomičite klizače [i]a [/i]i [i]b [/i]i istražite kako se točke sjecišta [i]A [/i]i [i]B [/i]ponašaju s obzirom na te promjene.[/td][/tr][tr][td]7.[/td][td][img width=24,height=24]https://lh5.googleusercontent.com/EeYLvel9HmsnYD7ZRVm-HBQtblHhlB35cdQzXdG11nyuG3R7BCgnyC_l3L8aKn1R4wNkQnlMJHA72jcGN8n5f2RRahLZMiuy01yMfDJFEssc0gxkkfajbgHSyt1KTilGP0RyH5NA[/img][/td][td]Označite grafove funkcija [i]f(x) [/i]i [i]g(x) [/i]i promijenite boju grafa koristeći [i]Traku stilova[/i] kako bi poboljšali svoju konstrukciju.[/td][/tr][/table]
Pokušajte sami...
Kompleksni brojevi
Zadatak
Odrediti kompleksni broj i promijeniti koordinate kompleksnog broja u polarne koordinate.[br][br]Istražiti konstrukciju i saznati kako prikazati kompleksne brojeve u polarnom koordinatnom sustavu [i][url=https://www.geogebra.org/graphing] Grafičkim kalkulator[/url][/i]om. Zatim pokušajte sami, prateći upute u nastavku.
Istraži konstruciju...
Upute
[table][tr][td]1.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/1/18/Algebra_new.svg/32px-Algebra_new.svg.png[/img][/td][td]U [i]Algebarskom prikazu [/i]otvori [i]Pomoć[/i] i izaberi [i]Tekst[/i]. [/td][/tr][tr][td]2.[/td][td][/td][td]Kopiraj sljedeći tekst u [i]Polje za unos [/i]i pritisni [i]Enter[/i]:[/td][/tr][tr][td][/td][td][/td][td]CCSS.MATH.CONTENT.HSN.CNB.4[br]Prikazati kompleksne brojeve u kompleksnoj ravnini u pravokutnom i polarnom obliku (uključujući realne i imaginarne brojeve), te objasniti zašto pravokutni i polarni oblik danog kompleksnog broja prikazuju isti broj.[br][/td][/tr][tr][td]3.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_complexnumber.png[/icon][/td][td]Otvori [i]Alati [/i]i izaberi alat [i]Kompleksni broj[/i]. Odaberi ga i pritisni bilo gdje unutar [i]Grafičkog prikaza[/i] kako bi kreirao kompleksni broj. [br][b]Napomena:[/b] Kompleksni broj bit će automatski označen sa [i]z[sub]1[/sub][/i] i njegove koordinate bit će prikazane u [i]Algebarskom prikazu[/i].[br][/td][/tr][tr][td]4.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/30/Menu-options.svg/32px-Menu-options.svg.png[/img][/td][td]Otvori opće postavke i promijeni veličinu fonta.[/td][/tr][tr][td]5.[/td][td][img width=16,height=16]https://wiki.geogebra.org/uploads/thumb/2/25/Stylingbar_caption.svg/16px-Stylingbar_caption.svg.png[/img][img width=16,height=16]https://wiki.geogebra.org/uploads/thumb/b/bd/Stylingbar_point.svg/16px-Stylingbar_point.svg.png[/img][/td][td]Izaberi kompleksni broj u [i]Grafičkom prikazu[/i] i promijeni mu postavke. U izborniku oznaka označi [i]Prikaži vrijednost[/i]. Promijeni i veličinu točke.[br][b]Napomena:[/b] U aplikaciji za mobitel otvori izbornik sadržaja pritiskom na gumb [i]Više[/i]. Onda u [i]Postavi stil naslova [/i]izaberi [i]Vrijednost[/i].[br][/td][/tr][tr][td]6.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/34/Algebra_hidden.svg/32px-Algebra_hidden.svg.png[/img][/td][td]Unesi [math]z_2=z_1[/math] u polje za [i]Unos[/i][i], [/i]klikni i sakrij novi kompleksni broj odabirom takve mogućnosti na lijevom gumbu [i]Vidljivost.[/i][/td][/tr][tr][td]7.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/4/41/Icon-menu.svg/16px-Icon-menu.svg.png[/img][/td][td]U [i]Algebarskom prikazu [/i]otvori izbornik sadržaja pritiskom na gumb [i]Više [/i]na [i]z[sub]2[/sub][/i] i izaberite [i]Postavke[/i]. Otvori [i]Algebra[/i]. Promijeni koordinate u [i]Polarne koordinate[/i] i zatvori postavke. Kompleksni broj [i]z[sub]2[/sub][/i] prikazat će se u polarnim koordinatama u [i]Algebarskom prikazu[/i].[br][b]Napomena: [/b]U aplikaciji za mobitel unesi [math]z_2=Upolarne(z_1)[/math] da bi se prikazale polarne koordinate u [i]Algebarskom prikazu.[/i][/td][/tr][tr][td]8.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Premjesti točku [i]z[sub]1[/sub][/i] u [i]Grafički prikaz [/i]i istraži kako se mijenjaju vrijednosti [i]Algebarskom prikazu.[/i][br][/td][/tr][tr][td]9.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/30/Menu-options.svg/32px-Menu-options.svg.png[/img][/td][td]Otvori [i]Postavke [/i]i izaberi [i]Prikaži mrežu[/i]. Aktiviraj [i]Polarnu [/i]mrežu.[br][b]Napomena:[i] [/i][/b]U aplikaciji za mobitel izaberi [i]Prikaži mrežu[/i] i promijeni [i]Tip mreže[/i] u [i]Polarnu.[/i][/td][/tr][/table]
