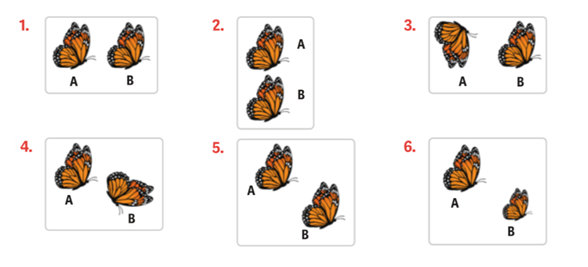
Transformações Geométricas no Plano
[size=100][size=150]1. Simetria de Reflexão[/size][/size]
1.1. Visualiza o seguinte vídeo onde encontrarás informações necessárias para responder às perguntas que se seguem.
1.2. Numa simetria de reflexão um segmento de reta é transformado num segmento de reta
1.3. Numa simetria de reflexão os ângulos são transformados em ângulos:
1.4. Em qual das opções a reta e é um eixo de reflexão que transforma a figura P na figura Q?
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmsAAAHHCAYAAADgeh/sAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAObKSURBVHhe7P2FfxxXtu8NP3/Q+7z33nMPz+FzhikzmUmGMpnJJJNMmGFCjjFMDjhxzCRZzNCC5m41itVqMTMz/p61drds2S67ocqyYP3yWXF39a6tXRu/G+v/gUgkEolEIpFo20pgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgTSQSiUQikWgbS2BNJBKJRCKRaBtLYE0kEolEIpFoG0tgLQ4tLy9jemoKY6NjBtto1LR+S8aM9o9t+/s5OjqC0bFBsiH6bmRYt/+zR8xoP40P4/jYOOZm57C+vh4tVaI7obW1NczOzFCaGJtfRg3PM8bnwYjdDn93gp8b/t2OcGpdT9aMD+PkxAQWFxejJWDnSmAthrhyGx0ZQU2wGh5XFYL+oC6rJgt4/XDY7LCUV8LjrlLXtNzGa8pPnx8uuxMOqx1+r0+3n2w+jxc2ixU2swXeKq+mm0TNT8/utDvgtDlUPOgJ58a9riorCqwXUWJLg8/rpuvVN7hNxNhfv8cHKz23k9Ip6AsYEp9VLjeslRaVTuynlpvELHDFT7cj4qfecHI+Yr/42d1OjkttdwkZ+emnvNTW0oqlXVBp7mTNzc2hubEJXrfb0DxorqyEy0l5UNNN4sZ5T5WVaL7WcpOIcV3D+dpmthpSj7Oxny6qyywVZlQ5XXTNmHBy/cDlz1vl0Sh/1/8Nre+brwVU2bNbbLBUmunZjUn3ALUx/OwOu121E1puEjV+XqvFEn12I/yMPDvXP709PVhdXY2Wgp0pgbUY4gTu6+1TGamhroE+96qET9b4/va2dgVA+Tl5qK+tU/5ruY3X2M/O9g6q4FxUIC1opUZRdzjJWkJhVJSVw1RSihBV8HxNy20ixmHjCpgLegfFg55w9vXQvd09CDQ48HXhm7hQ9h5CLbXo1xmffD+Hs6zEpOC3q6NTdzh7ursJ+IMoLixSgN7d2aUrPtW95Gd1IIiSomJ4qthPfeFk42flypf9ZLDu6eo2xE/O55yHGBZEd05TU1PUeHFnjtOW86D+8ldNjWJBbp7Kg5zP9fvZrYCiuIDKCvmpyp8OP9m4fvRSuSsrNamON+drLXfxGpeJTqq/3ARWRfkF1Mnx6feTnrGLwsngx3VuU4MB7Q1Ze2sbAWWlCieXQ04jLbfxGoezrZXqcYJzJ8FaSzis/o6W27iNwsTPW0bPbSqm9qahUfez95CFKWzcdoebmrGyshItBTtTAmsxxLA20N+PhvoGjAyPRK/q08L8AmqpwqgwlWN4cCh6VZ+WlhYRDjVT412tppuMEE/9+r1euF0uTIyPR6/qE4eNG20ujIsLC9GrOrQOdI8244x5HzLdH2NidjD6gz7Nzs4SVLnRWF+PZQMKOU//9ff1EvzZ0BpuwZoBvTz2s5cqNB6pbG1tobyqP5xcoXW0t8Nhc1AD16lGlvVqdWUVg/0DBOdtmJ+fj14V3QkxrNXX1qKnswPrBqStyoMEfZXUqWulBtyIaW72gzszdior7eSnEeVvaWmZ/GpBFdVlDAFGPPvi4pIapbSZK1VHaX1N/7OrerypSY0C8nSgEVqgMsdAzSNW3N4YkUZcjkMUTgYsnlbXr3WMj42qkT9+9vHRseh1fZqhsDU3NKGlOayWM+1k7ShYWx0fw7ylErPZGViqDmA9WojXF+ax6Pdijq7P5WZFftsAAcqYK10dmMvLxlxhvvqciK6BtVFjYI2ngmqrq1UFNzxsDKxxRuQMyb1GoxrE6ekIrPE0h1Gwpgp5FNaMmhJjWDtrfgtZVZ9gYm44elWf5uYY1qrQROlu1PD5QF+fGqnj6UAjKkwWNzwuh4N6ugSAa/rDyc/aQb17nqbu6uhS5UevGPgGBwTWrhHVXcvhEGZzszFvKsYypd9ilVPVbbPZmZjNon+z0jFL9dai04bVkWGsz82RGxdmM9Ow6HJgPYm4vAprnYakLYtHRczl5ZQH26JX9ItH/Ry2CKwZUf64E8J+eQjW+qnMGKFFAsDmphDBmhndFF4jtLS8RPV4SEHl2JgxwMLrtRjWeDZn2KgBB2pfm6OwNkcdWyPE61q5zuWRxXFq640Qh42BWmBtC8VANpOWgoFf/ARD9/8W82Wl3LKo31Y62jH2/NPo+69vof97/4Wxv76I5Zaw+o213FiH0eefxMAPv4OJdw5jdXAg+ktsXQNrI8ZkdB5RugJrQ0aNrHEhj8CaUVNNGyNrRsIah83QkTXSNbA2a0x8RkbWIrBmxPA5w9lmWDNixIr93Axrxo2sXYU1I0YLuAwJrF2rlfZWjL/2Ivp/8G2qkw5h0VuFsddeRv///Cv6v/uf6P8O2bf/nf79Dwz+4qeq3loM+DFz8RwGfvZDDP3xd1iwWaO+xa/NsGbYyNomWDOiE8J+bIY1I8ofN9SbYc2IcKqRtU2wZoSfPLJmNKwxWF2BtSGCfgPCyeV4A9aMGVljWBu7CmsGPTuHTWBti7VUV4uRR/6Evn/5e0wcPoC1DXighmChohyDv/wpev/uf6H3n/8vBu76IeZLiiO/k9bm5zBz7rSq/Abu+hHmCnKvjMrFksCawNpehDWeBhVYuz3iEbGZC2dVfTR4908wX1mBFapjRp99Ar3/8L8x8JPvY+SpRzFC3wd/9XP0fuvvCOL+HdNnTmKpthrDVA/2/tP/xfjh/VibSKxcCqwJrBkRToG1rdeOgDWu3KZPnUD/f30LQ/f+nHqUlugvBGKzM5j68jOq+P6DQOwHVLndTb3Rf8fU0Y+xNjUZdUWFgCqo4b9QJffPf4vxN17B2lB8a5sE1gTWjIK1foE1gTVKs+VQCMOPPYy+f/37CHBRPbU6PIzR555E7z/+DcZffQkrne1Ym57GgsOGofvuVZ3UyfffwUpPN6Y+P4q+/6C68Lf3YMFSGfU4PgmsCawZEU6Bta3XjoA1Xtsx+txT6Pu3f8T4ay9jleBpQytdnRh9/mkFa+OHD2DyvSPo+89/xvCjD10zFcoV4gT9xj3Soft/g0VPVfSXW0tgTWBt78KaMQ26wNpV8VramfRUDPz4exj86ffV+jTWKsWPGlkjWJs48CbWKf+xltvbMPznP6Dv3/8JU198ivWZacxbzRj45U/R/5/fInCjawmUI4G1HQJrTgM3GAisCaxtiShjzVeUYfBnP8LAd/8TM2dOXl1YS43AfLlJTRUM/vpu+lyGufxcqgi/i4Gf/gDzJUVEadHFqctLmL2cgv7v/w8GfvRdzFy+xCufI7/dQgJrAmtGwdpOmgaVNWu3R6vUAE8c2Ecdz3/AyCMPqmlNdb2/LwJr1JkcfeYJLNptqkM58eF7qs4a/tPv1eYC1nJHO0Ye+zN6/+XvMf7KC1jhzQJxSmBNRtaMCKfA2tZr28PaOkXwbFoq+v/rXxSEzRUXcGmO/DY7R73No6qHyRUcV3jLba0Yffoxcv+vaiRtbSKa6FQxzVeWY/Cen6GPe6TUS6XUi/x2CwmsCaztRViTadDbo5WeLow+9Rh6/+H/YPSl57BCeYKlYI2nQQnW+r//3xj63T1UV92lRtQGf/J9zJw9pZZ8KLcD/Rh/86/o/49/xuijBHzVAXU9HgmsCawZEU6Bta3Xtoe1NYrs6dPfoI8qJt4FtWC+ukaDd4GOvvAMVWj/jIm3D6lKbKWvFxNHDqLvW3+L4Yf+gOVQY9Q1Fa4qt1r/wZsQJt49zKUt+svNJbAmsLZ3YU2mQY3WEtVHI395EL3/+H8x/vorWIseUbBKeWMD1njkf/ih+5W7wV//AgM8svbnBzCbl6s6r6ujI5h87230//e/YuiPv8WC06H8iEcCawJrRoRTYG3rtf1hbXoaUyePX4U1qzn6C2VCc4XaUND7rb/DwA+/jaFf3032S/T/4H8I1v4Og+R+NjOdWyDlftHvw9Dvf6MqRB51AxWMWBJYE1gzCtZkzZrA2lJDPUYeju7mfPM1rE1OqOsRWIusWRt75QUsNzcpKOM6i3eGch038peHsFxfh7WJCUx+/IHaTcrHGC047MqPeCSwtgNgLSRr1gTWbtT2nwZdXMRsygW1aWDgJ9/DHK9D4+sU8dOnT6D/P/8lAnI//QEGf/7jyNq2u35Avc5/U1MIvFh3Y3u72llFPVV2L9OgsSWwJmvWZBrUWKnZgCf+EpkGffmFK2c+XlmzxhsMDr2F9flIGebzJbmu4lE0rt8WKsrUurfxIwfV0hAefVsKyjRoLMnImsCawNrtFlUo80X5ah0H20zqRQK1JdUTHXv9FfT96z+oKYK5vBws+jxYqHKpjQUjT1KF+E9/o6YTlmpruAaIbD74yfcx8KPvYJY3GFAjEksCawJrAmv6JLB2VavUWI69+rI6QoihbTnUFLlOdYwaWaM6a/T5p7Do9ai3GvAGqpEnH1X13NCv7lbHFqm6j9zwJgU+AHyFQCFeCawJrBkRToG1rdf2hzUSTwUM/+kPamPA5PtvY210REHZ4C/vimxf//Jz9SqWK6JE4QMkeXSNj/SYuXAO6+o8tqPo+xeq9H7/a7V+LR4JrAms7UVYk2nQ2yO1rOPrL9UbCniUn3e6s9TI2tOPo+fv/hf6v/tfGKY6aviPv1NLOfq+9fdqZI3X5a709mDJ51UbENQMwWefXFv3xZDAmsCaEeEUWNt67QhYWx0ewsTh/WpjwMhjD2GpphozmWlq4S0D24K5POryqhY8VRj6w+/UVOj42wexRD1V9UoqXivy2itYG5RDcWNJYE3WrAmsGSyKCz4nbfDen6slHNMnvlbpyNOhYy89q+or7oDyv3yuJL96auThBzBF7ngn6drCPHVET6HvO/+h1ujyyFsiEliTNWtGhFNgbeu1I2CNz0qby89R05cDP/q2msJcoZ7oUlMjlsNhNWp2vfigSD5QcqmhTh3nwdOnvOZt4Oc/xnxhvrxuKg4JrMk0qEyDGq/VgT6MvfmamtocfeZxNd3J4MQHfHN9xZsQNoynSXk0beNsyZXODow884SaIeBDwFfHEmvQBdZ20MiawJpuCazdAa32dmP8ry+i92//X/WO0KVwc/SX2FpqalDv0+PjPCbePqhe7RKvBNYE1gTW9Elg7TpROs2Xlaj1s7zubPr4l1c2FNxKa1Qep7/5Sm22Grrn51iwy4vc49WOhDWDgEVgTWBta0UVPp/oza+TmvzgHfrsVpsPYorc8H3jh97C5EfvYZnALRFthrVRg3o6S4uLV2BtJAFwvJU4I7aEW1BTXYO5eWMgaHp6Bn6fD1VUgCYnIkcM6BUX8g1Y43gwQj1j4SuwNjlnTHwyVG7AGucBI8T5iKcX21rbsQYDGjWyvr5+uJxOtLUxAOoPJz9rR0dnBNY6u7jljP6SvBhMBwcHBdY2aW1sFDOplzC+/w31UvfVON5VzK+kmj5/BuNvvYHZjDR1BmWi2gxrRqQtq7en5wqsGaUeAkCGNc4zRpQ/Br4NWONOkxFaWlpGc6gZNosF3RReI2JzaZk63eFmqnPdGDOog7xI9ewGrI0MGzPgwAC4AWtz1LE1QjwgsAFrhg0OUNgE1vaIrsBaXV2kV7K2rhqfZI17s/MEAjWBalSYylUjxs2ultt4jXtKXHjCVHhqfF7MTo5jfXkRa0sLSds62dToMPwuJ6ocDurpjNLf0f77idgMNTBNBGqNBEHzc7MqPrTcxWMbadE1HMIZgrVM98cYmx5QbdD1bhMx1gyBKvduOd151JLjmGEoYpvdX/9dw+hezkd91Kg5qGJvDTViZYGefVk77uMxTt/VxXn0drTDZSU/qYJfpoo+Ek6NMMRp/Kxt1KjZbXZ0tLdjlRo5vX5yJckNpMDanRfDWl1NDbop3+hNW76X8zWDH3c8W1p4dJfLg34/eb2k3WKlfN2yqfxp3xOPMbC0UvjcBAK93T3q2bXcxWtc98xTpzjU2AhbRSW6KW+vcflbWU7aQLZEcNFCflY5HRgdGVF1x7V/O476ZpNx/To3O4egzw9rpRlDA4PRNNJ2H49xO8AQxM/eUF+nZmD01OPKVtfU8/IsjsvhVJ/1pjkbh43DKbC2B8QZu7e3RxXygD+oeo+tLa1JG9/fRKRfYapATlY2+elHe1u7ptuYFib/6F++v40KTU12KgLHPkRfyimMZJ7HcOY5XdZz8Rv4Pn8fjjPfoMlbRX+Hnl3n8zfWU+VmtsJCFQePsDEYaLmLx9paImFxBcvxZcFLOG06hJoGL/Wgk49P/pfjs6GuAcUFRVTBVSoQaqfnbqPKXhmF+YrF/E5G8cbpXuu0w3ryGOpPHMVg+hnNOI/XVPpmnEPLqS9QdfR91OZloKOpAe0EWFf+7vXhuOHatWHlkYeW5ma4Cc4L8gtUnucGjq9vdneNXf+8GtYSDquefSP3wg2aohclp6nJSfg8XnjdVQqEOH1uKAdx2sa97FdOVo4ajb3eTaK24Sc32gW5+crPMOVJPeFkaw6F4LI7UVxYDK/Ho55dy128xuW5hTqdwZJSuM+eQ3tODiasVkzY9NmYuRLNmZnwXL6MZup4d3C9Q8+ujP/u5vLG36NpeMX4uwpfxLjsMqxUlJYhPydPQRuX6WvuifX9OmM/ucPNMG01mwnY6qN1BN+XpNHfrKmuRklRMdW7haitrlH1Ziv5e41x/F9/7SbGYeWwcV4Kh5qJhQXWdrV4HVBnZ4cq5NmZ2epfvVZIDWHKxRScPnmG/MyhDFqi6S4+o3sJ+so+egf2B+6F70ffRt1dP0DDz3+o22rv+j48P/4OrPfdjfIjb6LkcorG30/MCvIKkJaShsuXUikeCjXdxG+ReLucewbvXn4Cn6S/hNz8dJRErydrnB751FBcOHuBwppK14pQSn6W0m8JG1U+bCVpqTAdfh3W3/4MgZ98Bw0/05dG9dF/q3/yPVRRmtv+/DtUfPoeSrIyIn+PjcKdqHFFmZmWjvPUAGWmZ9C1whvcJGpFlM75uXkKEoyaMhElp0mCNbvFhhyuy6gzopX/E7Ws9Eycobos43I6+antJiEjPzjvnTtzTvlZZEA4iyhfs18Xzl2gOjdL003cxs+Yl49yCp/z0NuofvFVNP/1TbS/eUC/vbEfoVdeR5DM/umnMGVkorSY6h6qkzTrlzgs0t5cwrnT55BLbUUJxadWOU3ECvPzkZ6aRvXjZRRS2S7VcJOYFSIvOxcXKX0unDuPXPrM9W4kj26yBL5zmnM9zvUPw6URax/vpATWYoiHTrs6eMG1XY0OqBGWKLUnY3w/jyhVlJWrCjPoC6CjPUk/29oRrq1GzfnjcD14D+w/+zaCzz2I7o9ex8DRt9D/6b7k7eg+dH7wGvzPPQTr3d+G83c/RfDYBwj73dG/n1yYeY0Dr53gIflQU5Ou+Izc2wZXdQW+LHwZp00HUdvAvdHo6FKSxtN/PE3LBd9SWalGm3i0jv9eosbha/ZXIfDFe3D8+kdw/PJ7aHrtcfR9EoljzbiP1+j+0Lt/hfOJP8J+93fgfuhe1Jz7CuHqQORZuIeckLWqHqjL7kAhNUZqZC0cJr+03MZv7Cf36CNT3zKydid1dWTNrdL2lqOmMWzjXm9VlYIAJ+WbmCOxMUzdS35ERtbylJ88shYpSze6j9fCoRD5ZVedGF90ZE3LXSzjcLRS/d1UVobqDz6E79mX4N93AG1fH8fQhfMY1mkD586i+bPP4fvr6wi8/FfUnT6NcMBPfze5+oeN25vyjZE1v5/il8r0pvKZsFE8NDVGR9aoHm+oi46sabmN0zjf1AarFUgyZFXTZ66P+Loeq6+rU/UYbwRZWRZY29ViWOvp6kZddQ1GR4zZYHBlN2i5vt2gq7NTGK/MQ8vzD6Lu9z+GZ//zCKSfxoTXhKWaSiwSxCRrSzUVGKsqgS/1FMz7nkf1H36Glmfux1hhKpYnkl/Ez4317dkNut/Q3aBzc1d3g/L6lmS1PD6EkZwLCD32W3h/92NY97+IVorD+WAkjrXiPh5bIlsg67Lmw372K3hefxr19/8YbS8/gomKfKxOJ7dAd2M3qIMaScPPWSMIljVrd1Y7YTcoeXJ1N2ibwbtBCVL17Abl1xwutrVg6OIFtO4/BO/b78F26jQ6KsuoPPp02zR1hkMlhXAcP46mI++g++23MV5SgpUEj2jZrCu7QQmuDNsNuiC7QbdaAmsxdA2sjRqTga7dDZocXDCojZVnI/z0H9B4/0/R9fGbqMs+j0BhJsFaOZZqrVissSRtS7UWjHrK4MlLg+PSSbR8dgjhR+9F+Kn7MFqQgpXJ5HYV3Y7doN1jV4/u2E67QVfGhzGcdQ6hR36F5kfuRf2n+2G9cALh8lzMV1Mca8R7vMb3LpB12QrhzEpFA0F610evo/lPP0frcw9igv7GGuWRRMXPevVQXAN3g8rRHdtCt2U36BVYa49e0a/eTUd3JFv+NmvzblCGtWTErzmcb23G4Pnz6Dp0BN1ff42a9DRY0jPQZubOk5/KZPK2WBvAdMCDRlMJnJmZ6MxIR+8HH6Lz4GHqJBcQsCVX527eDTosu0F3rATWYiiekTVVEbS1o7y8DIVUqKxWK3puUSHoPWdtbWEO45YChJ68Dw33/RD9n72FCWs2msryCNYyMEGQpUCg2py0LdWYMeouhSc3DS6ygcpsDJ14F80P/4KA7fcYzb9EMBLfWyA2a6+cs7Y6MYKRvEsEar9G6MG7MXTqA3SaMmHPSkG4jGAtWIkljXiP1/jeBbJOygcMa83k55QlC/2fvoGmP/wELS88hAlbMdbmE+v1boysxXPO2vLKsto0kJqSgtOnT8HhcKhK/HpdGVkTWLvj2k3nrDGElJlMeOWVl/Hiiy/grX1vIiM9XfN8sisja0mes7a2tIi55iYMnD2Djv0HMXD8OMYqy9BYWgJLBsFaZTkWgtqjZfHaIgHbtL+K/CyGOycHA3YLJgvz0P3e++g8cJDq3HyqcxMfMLgysibnrEWv7kwJrMVQPLA2Tr2Azz47invvvQd/eeQRPPTQg3j88cdQVmbSzCB6YI1BbdJRivCLfyZQ+xH6CNRmHbmYCVSgyZSLQMFtgLWcyxh2lWLOmY/B428TsP0SzU/cp2BkeTyxkay9AGsrY0MYyb2A5sd+i9Cff0Gg9h7m3IXothbBnnGRYC3HYFhLUbA2R37OWrPQR8AWevDnaHv1MYL4IqzOxH9GXrywNjQ0iG+owfr1r+7Fz+76Kb77nW/jrrvuQgqB2/XxJbC2fbSbYG14eAivv/4a/vmf/hF/euCP+M2vf0X58Dv44ovPFchtlh5Y42M15luaCdTORkDt668xYynHtC8CVhYCRKNhzZWdhQGHDQuBKkwU5KLnfQa2QxgvLcXq1GQ0ZPFJYE1gbU8oHljrpcL/wgvP44Xnn0eYMoXf7yNoe1hBWydPN1ynZGFtdW6aGt9ChJ97gEDtx2pEbdaZp6Y8ZwKVBGs5twfWslMVrPHU6KwjHwPHDiP0x7vQ/PjvMFaQipWp+AvWboe1lclRDOecR9Off4kmiqPBb97BvKcYasrSWnB7YC2TYI1AfS7I6WbBjDUbvR+/jkY1wvYgJirzsDYbXwW/AWu3ejfoxMQEPvzwA/z8Zz/Dl19+qY5F8Hm9ePLxJ/D739+HmpqaqMuIBNa2j3YTrPHC9BeeexYH9+/H2MgI/f0W/PXll/Dgnx5AE4HEZiULa+srS5hvb8XA+fMEagfQ/9VXmCZQuwJWJbcT1qxqanQh4MFEUT66GdgOH8G4qZTqmfg7YAJrAmt7QvHAGlcCTzz6F3zy0YeRC1QJfvbpJ7j3nl+qs2OuVzKwtjo3hbGKbISeug/1v/0R+o7ux5yzQDXOqoH288ja7YS1kqifDGx5BCFvq3VYLWpKNEUtpI9HuxnWeOMFgxpPfTY9eDcGTryjRtQYphmsugisbiusEbCrNKK0m7Fkoe+j19WUaOvzD2K8Ihers7Er+FiwxuvPrDYrfvGLu/H2kcNY3jSCUWEqwz2U58+cOX3NfQJr20e7CdZqgkE8/pe/4Juvv1bfV1eWcfrkCTz84IOq87BZycDa+hKBGo+onSNQO3QEA998Qx0hXpsWBSseWbvdsEbXFhjYgl5MFheg+4MP0HHgEEYTWMMmsCawticUD6zV1dXhwQf+iBPfHFff+Z6jBGt/uO8+lZmvV6KwtrYwizFLPpqfZFD7AYHaW5hz5FOviwqzWqhOjfNWwNrG7+T3fFURhk69j/DDv0T48d9iNO8i9fZiT4nuVlhbmRrFcO4FND70S4QoTobPfoh5T4mKK47LBYKzrYE1+j2a9jOWbPR9+iaaHrhL7RieILdr89PREGtrA9ZuNg3Kjf0nH3+M3//ut+oIhM2qrg7iD/f/njotH2F1U8UosLZ9tJtgzelw4JGHHkJ6Wpr6Pj09jXfeeRvPPvO0CtNmJQprDGpz4RAGzpxFx1sHI6BmozJXS/CkwMq3dbDGv/O/DGw8wvbuexSmAxgtyMPqRGyoEVgTWNsTigVrnPEtZjP+9If7kZmRob63trXiheefw74338CoBowlAmv8aqFJhwnNz/4B9b8jUPtsX2TqU42gRBrlLYc1AkQGxTlXIQa/fhuhP/0c4Seiu0RjHOuxG2GNp4FH6NlDf/kVGv/wUwydfg8LXgK1WlskLsm2FNbYTTR/zNpy1Bq2pj/+BG2vPEJ5qYSA7ea7t2LB2gBBF089PfPUk1Qerk1rnv7kKaiPPvwAK9TYbUhgbftoN8GaqbQUv/3VvTh58oR61VVqair+RPnvzOlT13QWWInAGq9Rm1MjapE1an3HIlOfCwRoCpoUWG0xrLHVBjDPU6KFeeh69101LTtOblenb73EQWBNYG1PKBas8e9ZmZn44fe/h0f/8gjeo0L0DPXsXnrxBXUAoVaFGC+s8U6+CUex2tnX8NsfRNaoXRlR29RwbzmsXTW1hu2rI2j+8y/QzCNs+bc+1mO3wRrD6XD2BTQ9fC+a/vQzDKqpz6IILEXj6I7A2oZx3uAp0Y9fVyNsrS8/onYS32zTwQas3WwalF+w/cRjj+KN115Vp+FvFk893X//7/H1V8euOZtOYG37aLfAGuepjPQ0/Nu/fAs//uEP8MjDD+OpJ5/E2dOnMazet3yt4oW19dWVyBq1c+eiuz6/xrSZQKzaexWaFFjdAViL2nygCuNFeeh5/wN0HjqM8bJS6jDefImDwJrA2p5QLFibn5/DN998jR9877tqxOHop0eRToWXDwBV4oJxXeGIB9ZWCdTGKnMRIgCq/8331a7PeXcBFV4uwNeC2J2ENQ7LnKsAQ9+8g9CDP1M7INUI25T2OTm7CdZWCHiGcy6g4f670Pj7H2Pw5Ltq6pM3YmyOozsLaxQWsllrtgK2xvt+hPDT92Ocz2FbuLGSjQVr3dSIPkadkn1vvKGmnTarqLAQ9/3ut8jLy6U8f/U+gbXto90Ca9PUCB/78ks89KcHUJCfr5aidNE9V9ZQXheOeGBNbSZoa4msUYsezzFjrbwymrbZ7iSsRcLjxWRJEbree1+NsI0VFWJlXHuZjsCawNqeUCxYm6TK7/333lULXRWALC5dWwlqVIixYG1tcQ7j5vwIqP3qe+g7uk8B0c0A7I7CGhv9rXl3oTqigg/ObX7yd9Fz2G6cEt0tsMajhyP0jKE//0pNAw+dfh/zVcU3jHqy3VFYi5rKI7yG7ZPIlGgrn8NmKcTa/LUH527A2s2mQfuooXvy8cfUNP/ExFUgHx8bx4H9b6nRZX4Bs1K0URBY2z7aLbA2ODiIQwcO4M3XX8M8ldVYigVra8uLmA83YfDMGXQcOIyBEycxY6cytmnqc7PdUVhj4+sba9je4zVs+zHG57BpvOlAYE1gbU8oFqyNjo7i9VdfxSsvvYixzWt4uEDcpFDcCtbWVxYx6SpF89P3o06NqBGoOfI0IWDD7jissSlgK1IH5/IZX6FHf4ORgktYnb42znYDrPEU4kjeRTT+6RdoeuBnajPBgrdUxYFW3GwHWIuMsJkja9goTzX96a7IsR58cO7C1cYuFqyNUX5/68038etf/Qq1dbXqGlf+WVlZ6ry1L7/4/Gp8RfO/wNr20W6Btbb2djzz9NM4fPAAljetj7yZbgVr6hy11jAGGNT27cfAV19dHVFjWNOApTsOa2z828YatnfeVZsOxoqLqM69tgMmsCawticUC9Z6enrU7qMjhw6qlyTHo5vB2trSPCbdvJngj6j79ffU1OeVEbVbwNe2gDU2+pu8hm3w2GG1fqv5ieiU6OTVeNvpsLYyPa42EzQ+fA8afvdDtUZt3stTn7eAabI7Dmts0XykgO3jN9Shyq0vPYxJO286iFS4G7B2s2lQbhhNJSW45xe/wJ8feggnTpxQO/Du+eUv8Mbrr6nyoMQNQrRREFjbPtotsBZuCePVv/4Vp06ewBrlr1i6GaypNWptLRiMrlFT56iZyyLgdQtQ2hawxrYJ2PhNBx0HeQ2b6ZqDcwXWBNb2hGLBGo+s5efnweVwxNXDY10La5HROD7wdtySFxlR+/X31WaCjTO6NBveTbZtYI2N7uM3HfAaNvWmg8d/o950sDIdKXw7EtaijQHv+hzOPofGP92tRtTUGjWe+owR19sG1tgUsFF+MWehV02J3oWW5/6E8YocrM5OYoUa8FvBGmtudg4lRUV49ZWX8dSTT+AXd9+Nu3/+MzidzqgLEt8XvVdgbftot8DazMy0etUZ/+14nkMT1laXsdDWSqB2Xp1dNnDiG0xHz1GLZdsG1jYsSMBWUqg2HfA0Lo+wLUdfTbWwMC+wJrC2+xUL1jjjc2O0zg16nJXfNbBGsIeVBXVoaRPBTd2930Hf5wRqN1n/pGXbDdYYMCPnsL2H5j/fjfBjv4nsEp0axRwV8lBjaOfAGoWTAYbPJ2PoVJsJ7v8Jhk5/gAWvKT6YJts2sMamgM2CWXsu+o6+icbf/QDhJ3+PSXMBlqjT0NnZBafNqTkNulkz01MYGRmBiyDtqaeexEsvvghPVVXk2IRNDYLA2vbRboG1axTH37wCa243+vr6sLq0qF7Krs5R28+gdiK6Ro3gKA5A2nawptxFD859J3oOW36eOjhXwVpAYE1gbZcrFqxdERcArvziKAgMKexfZUUlBnu6MOUui4yo3UOgpjYT5McFARu2rWCNLQoDatPBSX75e/Tg3PyLmOrrQijUTLDWtM1hbU6BR1MjQeXYEEYLU9H0yL1o5M0EZz6IHHgbL0yTbStYixrnEfVqKh5he+AutL38CEYrC9DWUAuXwxUT1ja0vr6GOgIA3mhz9sxpLMzNRX+JSGBt+2jXwBr/nevtFtoMa71dHZhtbsKgetfngasH3vL6tDjhaNvBGhu73ZgS5YNz9x3AeHERZgb7UR2shtViFVjbwRJYi6G4YC2BSoOlYK22DhUFBWjJuqBeB6TOUft8P+ZdhViutamGNF5b5nd2UkMdogY7UJCJSW85XbNquo3X2M+xKtMVWBshcFvWcHdLozAsMLDxwbkP/EyNsPVcPolGt0NNhV7/suVkdTtgjadrPR4P6lx2DGadVa+P4ndtMqgt+iIjaprPrGEcbwxH3ZZCBWstZblUuZoTj89Npvwk6yI/GdbCpjwCQPKT0k3L/U2N3M85cinvvUVpdBdC1GmoOfcVHGVl6OrqiQvWNrRE+Xp+bvaGxkBgbftoV46sxSEFa5T/qthPq1ltJujafxCDvJkg+q5PZQQ9Vz7fwpZq/ZjxedAUhbV2grXFoLbbeG2pNkCdbvIzCmuDBGt8TcvtTU29msqDSQK2nnffR/fhIxjIy4Ov0gybWWBtJ0tgLYauwFpNLcZGjclASwQpDX4fyj55B96Hf4n633wXPZ+8gWlHHuYCFZj1l2PWVxa3zfnLMOkpRWNxJvx5lzHqKqZriflxvbGfQ44iVGWnwJV1EQP2QsxpuLulcRjIpixZ6P3yAJr+fDdqHrkH3i/eQ4gqpaU41/jFUs9YGOcs+5Fd9Skm5279BoV4xZWR11wO92dH0PBnSqP7foS+rw5j2pWPuSClkdbz3sJmCPA6KnNhSz+PUGmm+p5wfG4yvneGrJ38dGRcQKgkC9Ne8pPSTcv9TY3TKFCOiYp0dH/wV9T+7gdw/fke2L/+FD1tLXF1PmKJ3yc6NDgosLYNtAFrvQRDRqQtq6+nB+aKCoKh6NmSBogB0GmzqzzDsK9XDHydBH7urCzUfPIJ2g4eQu/XX1O+N1H+9yRsc2QTHhcaiotgSUtHSwWVR6rTtNzGa3O87sxLfpYUEaxlos9OHamgV9NtLJvxuTHGu0Q//ADNb+2H68sv4SwpwehwfO8TjSXetBAOhajT3Yi5OI5OiUcT4+PwVnngcbnVZyPEYQs3hQTW9oI4gTvbO+Am2m+oq0cvVUx8inuy1tvdQxVQKzzlBSj64FWUvvoQrB/9Fd6ck/CXXYa/NBW+0pSEzE/mLb6EypwzMGWeRlXxRXVNy228xve7ii6imPwrzjgFV2FyfvLz8H2e3FOwH9uPsn2PouzDV+laNlWeLSo+tOIpHovc2wNfgw1fFb+CcxVH0NRSTY1H7w1uE7Feur+tpQWW7Esoevs5VLzxCOxfvgVv/hn4TZHn0XrWWGbLP4/CtJOozD2rvutJo417lZ/p5GcO+VmSnJ/8TL7SS6jK+BrWj1+D6c2/oPLzA6h3lqO7s0Pt8OymeLmlUYdGWWenOjhXfY7+1tnRiXrq7HDFPn/dFKloa8Ww5vd6EfT5KK26KL/rK3+cztV+Pwry8tSoCH/X6yd3jgM+P4oLipSfnR0duuvdro521HiqUJl6CRVffgrH6ePwFGTDbzbBbyEzlyZs3soSVBblojAnHdaSPPg03CRqXnMJzORnSV4mXGVFdC25sPktZfBXlqIqMxVWel7TsaMw52aiqb4+mkbJG6dRG4Ov0wmn3a5ASE89rozCxKN0ZSUmmIpL1VrhuOqdGBamsHmrvAosBdZ2uTiBOWNyBiotLoHdYlULNZM1vt9iMSOvrBDnC1KQkn8W6QUXkEYwlFbARp+TtMt555Caew5p+dq/J2qXyZ8U8jOF4OIyQYGWm7iMn03ZBaTmk390La8kCxbqjdo14ih+47SwIo+A8MOMp/FF9l9hqiiAw2K7zl1i5qA0MleakVmSi3MUB6kUB+kc/qJL9DzJp9HlvPNIyaE0Iv+0fk/GOF04fXT7Sc+XTnCeTmmUQml0mZ6zsDSX4qGC8ivlWYqXuIzizVJRCSt9ZuNrZvpeVlKKYCCAuTljeuGi5MSvCOMRq+KCQpU+Wvk/frNSfWZBCfl16cJFBWza7uK3jfqgMK8AqRdTkJ+bp/KUTWe9y+9vLi4vxWVTPlJK85BWlo906jDrsbQyCiOVkZTiHPqX/dR2l5CRH5fJz1Sqe4wIY3pFIdJMebhIlkbwV07lWSt+EjKuH8srkJeTh9ysHFSYyind9KUPG9cR6alpSEtJhYk+8xq7G+qXBK28rFwBIHcUjZhOv5MSWIshhjU+wsBbVaVeFsyHgo6OjOiy3v5+mBvrcN5jQYGXGjOfFZXKLMmZ34pyTyXyyvOQU5yFMncFzHRN022cZiYzOcuQVZiBzIJ0lDpKNd0lZH4Liug50+m5S2u8aOvu1Iyf+C2SFnWtbhwvfQ0XLe+ioyeE8dGx69wlZuOUxpxGRXUBnHebUeKlyklnfLIVWYqRkZeG/PJ8VHrNmm4SMso7RZYiZOano4D8rGA/dYWT8hH5meMqxyVnJcwNQYqHPsrzIxgZGU7Y+EXv/O/QwKDq2bLJyNqdFY+s8TuLG2prMTI0hFFKW60yEJdROeH0bayvU/BXHQhiZFjDXQKm8trwsNqwwg12kPzktxXoCidZD+Vje2MtLnvsyPE7UV7tQaVOKwu4kWc2UWcnB4W2Ck03CVmNB+X+iJ+ZJfkoqbLRNa+22wTMFKxCqseB7KAHzVTnRsqmdjzFZZTu/CYTHqHlaUseSedrmm7jNA4TD4pwR49BkNcqcprzdT3GYeNjS8KhZmrLBdZ2tRjWeIiWp3HGDFr0OL+8hKrOVqRQYbe0NKC6px3B7rbkrbcDvvZmmFwOFFDPqSrchGq6puk2XutpgytUTwBoQk5pMZxNteqapts4LUBma21CHkEQ/ztm0ChLz3hkzVqW51NMzRuzZm1hZRnmliZcDrrhbA+hultnGpFZqn3ILCqAqcqBQFcLxacOP+neQFcbzEEvsouLYHI74e8gP3Wmu6+zBaWUPuk+FzyURzke9IoXNPPLtTvb22XN2h1WZM1aXWTNmkHiNWuW27RmjTcF8JpHvVqgejzQ1Y7Mai9MoVr4OL/3UFlJ1lSdG0apy06d2Xzq3Hqo/FB51nKbgPmoDJc6CSipznUQXAZ7OzXdJWLujlZk1/pR0FiDwZn4Dm6PpcXFq2vWjOqA8evrNtasTW56lZ0e8UYxWbO2R7QBazGP7khAc0uLcDOsUY/H0kog0N+NYF9X0sb3+6jhNrndKLCYUdUW1u8nmaslhDyqhLNNpXA2N2q6S8QCZDaq4PLqA7C2NGJ05toXgSer27IblNKoMtwYgTUCmOo+ffHJla6lJohMBiuPGwGuSPX42U9GfpqrA8gqKUYZ+emnxkJvuvvIj9K6agVrVdRwcDzolewG3T7aq7tB5xYXEehsQ1a1B6WhOvi4U6OR/+M2rnMJgkrdDmQWFsIc8EXASsttnMZ1LtfjpdTpzjGVwNFUp7s8s7nJz+w6grWGagxMTRiyr0R2g269BNZi6HbBmhpZ24A1LlRc0JM0VcipIjK5XQRrlQRrzQb42Umw1kSwVh6BtVADFXxtt/FagMxGYdtxsEbQojc+uYdrqQlchTXuhevxk9OC/LwKa64IrOkMp2os6oICa7tUAmtRWONRbY38H7dxncujYJthjTtgWm7jtEg9TgC4Gdb01jtk18DapMDaTpXAWgwJrAmsCazpk8Da9pHAmsCawNrOlMBaDN0OWJulBlBNgwYE1oyQwJrAmig+CawJrAms7UwJrMXQ7YO1FoE1gTVtt/GYwJooCQmsCawJrO1MCazF0O2ANW4AZRpUYE1gTbTVElgTWBNY25kSWIshgTWBNYE1fRJY2z4SWBNYE1jbmRJYi6HbAWtX1qwJrEVjRJ8E1gTWRPFJYE1gTWBtZ0pgLYZuH6zJmjWBNR1+CqyJkpDAmsCawNrOlMBaDN0OWOMGMPIGA4E1IySwJrAmik8CawJrAms7UwJrMXRbYU2mQaMxok8CawJrovgksCawJrC2MyWwFkMCawJrAmv6JLC2fSSwJrAmsLYzJbAWQ7cD1mTNmsCawJroTkhgTWBNYG1nSmAthm7fyJrAmsCaDj8F1kRJSGBNYE1gbWdKYC2Gbh+syTSowJoOPwXWRElIYE1gTWBtZ0pgLYY2w9rYqDEZaH55iWCt7bbBmqedYK2/OwIDSVpNfxdcFLYrsNZMsEbXtNwmYrb28BVYG5s1ppD3jIWvwNrk3HD0qj5xGm3AmssAWKu+Hta4sdCTRpwW5O8VWPO6yM8OXemu8hEB32ZY43jQqzWCgqHBQYG1baANWOslGDKk1Sb19fQoWGtva49e0S8GQIY1zjMM+3o1v7SEQFf7FVjzGwBr/utgrTp6PVnjsqs6SxuwRuHUW4+zualMb8Da4NRkNEb0aWFhAeFQCKHGRszNzkav6tPE+PgVWOPPRojDJrC2R7QBa7XBagwPDqmGhysPPTY9PwdXe2QatLKlSY04+amhTdb4fo+qOJzIJ1hzt4RUw80jLckawwQDWm55GbJLi+FojFRwWm4TMSsDYB3BWrgBI1MTmvETr62tRtKic6gRpyvfQqb7Y4xN96sRg+vdJmJ8/wylUSU9P8OaoyNM8aEvjfjZzRuwVuWCn3rQG9eTMk4Lqti5kcgqLiY/napXrifdebTPS/mohNInzeuEq60ZM3NzuuNzaXER/X19AmvbQAxrdTU16GxvxwrVbXrqM76XR726OztRSbDWEg5H/NRwG69t+NnV0QGbxYJW8nOR8o+ucJJxPvZ3tCKTYK0kVAtvd7T8JWvROreEwCqjsACVfq+CQa1yFa9x2fVSZ7bEaVd1rr2hVnc9zsadzexagrX6IPrGx1T86k0jHrFqIlBrqKvD1OSkrvRRRmEaGR5GlcsNt92BUfqs20+yqYlJNDU0CqztBXECd1CP0VJhhtvhRAP1Sutr9Jm/ugb5XjdOV9mQXuNFPhWiPJ2WS4Ux1WnBpbIS5NksKLJbUWTTZ3kEahfS03E+NRW5ZaWabhK1bLJLDjNyquzwBAOa8RO/1SkzuwtxNO8FfFP0Fjx+Gxpr669zl5hxGgeqq5FZ5cAZSqPMGp9mnCdq6R4nzlP6pJvLUeiwacZPIlZotSCzqEilT1peHn0360539vNyZTnOWcqRT+ENVAejeb4maeOODpcdjts5ajRFd06T1LDy6IXNbFWzBTzKdn3+j9vo3jr6105+Zaalw1xeoUDQCD9tlRZkZ2QRBFao/KO33g2QH8UeF867rUihDlgudUi0ymgilkN1bordgnMlhcikulJ3nUt+8czI5dwcKtOXkWOiOteIepzagwt2M1JdNjj9ARW/WnEUt1FaBH0BlJeWoazEBL/XF0lzneZxu5Gfk4vc7Fz1WW+9w3nR7/XCbrWhuSlEHQn90+l3UgJrMcSw1tbaipLCIspIeZQ5S3VbscmES+YynHRZkBJwEwx4qcenz9KDHpyliuhkeTEuFOSpAq/XLmVk4sSZszhx+oyCNi03iVgq2cWCfJwpK8alShMKS7XjJ1HLKDiH99KfxKcZL6OgKCtaiWi7jcfKyYopbBcojU4RrKUFqzTjPBHLIrtMaX3GacZpArZL+fmacZSonb98GSdOncHZS5eQmp2t6SYR4zQ6m5eLE6ZCpFaUooQaDI4PrXiK10qLilGUX4AAVepGTZmIkhPDGjdeeVk5MBWXaKZXopablY3zVE9kUX2h9XsylpNJfp49h6z0DJQaEE4uz5crTDjlqMQFnxMZ15XPZIzr3HMeO06YS3Gu0JjynJKdhTMXL0br3AxNN4naJSrPp0zFOEv1WX6ZCSaN+EnUSqhMZ1L4Mi+no7igiOpcqid0GPtZmJePS+cv4iJZAXU+r/+biZqppITCVqiMRwGNWPt4JyWwFkMMazwkz8OznOAD/f1qSkePtXZ1orQ2qAp7oLsDXWMj6BgdTto6x4bRONCLooYapHocKCZ/LTVBWOlv6LGyKjfSqACl5uSoKVarTj8tZCVBLzI8ThTX+BDqaNOMn3htoC+SFoGQA1+VvIrzFW+jua2e0mjwBreJGKdxe1cXimr8yKZwNvT36k4jtrq+LhTU8xSjC6agTzOO4jaVFgE1msaQxtPV5qD/RncJmpmeObfKgUtOC8rrgujo7sKgzjzf092Nhvp6tSB5XkbW7qh4yirg86EmEEBfby/6daUt39uL2mBQNbQ+r5f83Lh+vdv4jMteH/1bHQiimDrIPo+X8k+PrnqX6wkuz5X11cigjpejrRmtw4Po1Cij8RrfGxrqR0W4ASleO/J8bkPq3MqAT42oXc7NVmvXtNwkamXVPqRRu5Dpr0J9W6uKX614itc4LTq5TXS74XY41CYQI9pFHv2qoI52ealJfdbtZ3+fGmjh0bVwqFlG1na7NtasGbkbdHphnioMXmgfRO/EGNbX17C6tpq0rZGNz83C1hZCVh1BAP2ruSg2Advru0FnFxdhpjCWNtZifHZWdxqxDU9PwEyVey49P+8w1YqjuE12g4qS0F7dDTq7uABvVysKG4KqY7uwvERlUl+ZnqJ6nMsgr4MzhepU/aZVpuK1yEaxrdgNqj+Ndspu0BnZDbp3dC2sGZOBpqniYFjLp0a7bzLqJ8FA0oZ1TG0FrPVru43XboQ1Ywr5Zlgzajfo3NJSFNbqKG55NIgqOK24T8BGZgyENU6LLYA1o3aDCqxtD22GNWq1o1f1aTOsGaXNsMawr1fc6diANR4RW17hhlu7nMZn6woAq3s6dxysGaGF+YUrsGbcbtDNsCa7Qa+XwFoM3c6Rtc2wxiM3yRrdTZAiI2u3Z2StjuI2AmtacZ+IDRsJazKyJkpCMrIWgbUlgjWtMhq/rWNmh8KaAUm0Y0bW5Jy1PSSBNYE1gTV9EljbPhJYE1gTWNuZEliLIYE1gTWBNX0SWNs+ElgTWBNY25kSWIshgTWBNYE1fRJY2z4SWBNY242wNrU4hs6JEIZmurGydhXKBNb2kATWBNYE1vRJYG37SGBNYG03wdo61tAx0YiTgQN4vfzX+ND5FFw9xVeATWBtD0lgTWBNYE2fBNa2jwTWBNZ2E6x1T4bxlfd1HPe+gaqeUpyrfhdH3S9iYKZT/S6wtocksCawJrCmTwJr20cCawJruwXWllcXYWpJwRHLg2gc9lCaziO97ijB2gtqOpQlsLaHJLAmsCawpk8Ca9tHAmsCa7sF1sbnh3A28A72lf8OeaGTSG/4HJ+5X4SzswCrMg269ySwJrAmsKZPAmvbRwJrAmu7BdaGZ3pw3PM6XjPdi/S6z+DozEfnWCOWlrm+jkhgbQ9JYE1gTWBNnwTWto8E1gTWdgusjc0N4mzgsBpNG57txcrqMsIjAbSMVmN1PZJnBNb2kATWBNYE1vRJYG37SGBNYG23wNriyhxKms9jX8XvkNl4TE2FflH1Cjy9pVhbj7yiTGBtD0lgTWBNYE2fBNa2jwTWBNZ2C6yxBqY7kFLzEd62PYJPXM+ioj2d6qyr7YrA2h6SwJrAmsCaPgmsbR8JrAms7SZYYy0uzSpoG58f5MwTvRqRwNoeksCawJrAmj4JrG0fCawJrBmQRNsK1m4lgbU9pM2wNjZqTAbiQr4Ba/2T45GLXIKSNdLU/BzsUVhjaNMqtIkYw5rbYFhjs2+CtbFZYwp5z1j4CqxNzg1Hr+rT3NLSFVjjuFXSivsEbGRm0nBYs1yBNbduWKsm818Ha/PLS5Fn16E1goKhwUGBtW2gDVjrJRii/och6uvpgaW8Au1t7dEr+tXb3QOnza7yzOqqfqjkTgd3RDZgbVkB4I1lNBFjAKzu6UJmjQdlBGsbZSheu8E9lV0/wZqJYC2XYM3ZVI8aunaNm+vsej+0wlBFz50ThbXBqclIhOjU4sIiwqFmhBqaMDc7G72qTxPjE/BWeeBxudVnIzQ3M4twU0hgbS8oAmtdqK2uxvDQkGp4eKQgWVsjU6NgrSFVgNpHh7FAYDBHBT9Zm19cVIWwkuAivcZL/zbAQ71IPealAm4jQMuuLEdmWSksjbWa7hI1MwFgdq0f5uYGDFOYteIoXlujSpwr8s7hJpwx70Om+2OMTfVTGq3f4DYR4xGH6bk5VDY3UuUeqeDmqbLXivtErGdiVFXq2bU8+tmkGT9xWzdZZwvKA15kUMVe7HHB3R6Gt7tN230cxiMP7o4wimsDuOx1wkUdimkCVb15fonyd39fn8DaNtAU5eWaaj9CzbWYnB6ifD6KqdmRpEzdOzOC5pZalJjyUdcUwCT/ptPPydlhhMjPssoi1DUGqEwP6gon28BEH3WQ66iD7Edtbzcm52cVwGmV0/hsUc0McD2ZVu0mEPLD0d4AZ3tj3ObQuGYL1yLfWYn00gKU13nh6mi6wc1mu94PLT/NLXVIpzBm13nQOtQZSSMdxmkxPNaH6loP/EE3Bka6dKcPW3dfK6yOclhsZeqzbj/nKN2Hqe2mdrYlHBJY2+3iBO5sb4fDakPQ50dbSwtaw+Go8efErI3uq28iCAh4cMHnQnlzPTW6raiihjdp66BM3tpEBdKLs147Mqinl08ZlCumpK0ugOwghdFShvOVJmT53druErRMgsmLHgfyvW5UNzRQIdKOp/isVf3rDJThi4KXcLr0AGqoQmpvabvOXWLGaVzf1IRcfxUuBdywUNwyzGjGfQLGEJ1GldsFrwNZFA9a8RO3UfrmkaVXOXCu3IRUl5Xg36ftNgHLJZBMJVA757KgxO9FQ6hJxUcL5VtNox6r5vVNFqK4DFDZaayvN6wXLkpOk1MTsLiLkF75BZXBr1DgO67L8slSzZ/gWPZbuFjxofqu5S5RS6n8GF/lHsDF8g+R5/0aBf5vNN3Fa7nek7joTsV5TzmKGqsJYpqp3gyrzkmyxh3uXCqDp6sqyUy45NVvF6pKcMqcg2/KMqgMFmq6SdQueEpxwlWKU85sZHhOa8ZPopbjPoYLpvdxrvQ9ZLu/oPTRdpeIZTg+w4mCw/gm/xAy6XOhbj+/Ro7rGPKsZ9HQHDRkOv1OSmAthhjWOtpaUVFqQkVZmZpPr3I6o8afEzSHEw6nAzlWM87YKpDmdyGHGsjsGj3mRRaB2qUqGy5QI5sVrEIe+ZlLv+VtMq3vt3KTHajCBXslLlA4swlcrv9d67vWtWv8JAC87LQg11IJu8OhHUdxmtvpVv8WV6bjo6xn8GXuazBbi+FxRdY96DG73Y50SwUuuK0KrLKpl8sjYskZ3+tVaX3OUYmUKjtyqwmsNsVLMsb3pxP4nrOU47Kb/KRwarlLxDitLhMAXrCWo9BuhZPzOaWTm/7VNMrPsb47bTaYKypQHQgKrN1hTU6Oo9SRiWN5r+Lr0pdw3PSKbvss/3m8m/YYPs19VvP3ZOxo3rN4L4P8zHuGwvmyppvE7A0cL/sMJ605SPHakFntRiZ1nPRYesBJ9YOZ/CzBGWcJdUL124WqYpy25eIbc7aCNS03iRoD4AlrHo6ZvsFXpfs14iZx+6rkJXyS+ww+znkax4qNyUdfFL2IDzKfwAcZT+CLwhfomv50/6r4FVwo/RC1IY/A2m4Xw1p3Zyd8Hg9aW1owNjqK0eGRpG1sZBT9/X1w+ahhrSiDvyWEtpFBtAz1J22twwMI9ffAXhOE2VuF5r5udI0No3N0KGnrGh1GqKcT5W4nTA4bGro66Lo+P9nCFDZXMACv34+Bvj5d8Tk2HLm3rrWKCuZruGR5Dx09IYyPjt/gNhEbHx1Db08PKh12WPxehAZ7VRxrxX18NoDwYB98PK1qs8BVV4N28o/jWCuO4jF1L+WbQHMTSmxWVLGf9Hf0+Mnpy+HyNNSh1GpFbUMDRoaGKJ6HKV6St+HBQYRDIWXzarOG6E6Jp0GrfFbYfIWo7bChvtOetDV0OlBHflj9uUjNP47yqiz6ru02XlN+0r9mXy7SS04qP2vbrOq6lvt4rabNRmW5DEV26nA31SE00I3mwR4d1osGXjMa8CDXbIKz3k91cBuaB9qTt8EO8jMMa9CJIpsJgdY6qjc6tN3GbR2o72pGqasCWWUZVPeUGpJGwZZK8jMDxfY0+ELlutOHzd1QgmzTWWSXnkFVfYkhfvqbKmHzFCPUXEewJtOgu1qRNWvdqKsxbjfo4sICasm/yvJyDFJDtk7XeF1QssY7kxYXFxBubkZ1sBqzs7O8d1Fd12Ncsfu8XjXSND4+ZoifHLZQYxNCDY1YongwQmo3qGU/sqo+NWw36BxBBe9M4qm7peUlFXatuI/H+F5eu9XX2wuH1a6gf2V15Zp4Sdjov7W1VQWVToeD/AxjhfKq+kXLfZzG+Z0XijtsDnR1dNI1/Yu7eZ0m7wbtbJc1a3davMGgrqYW3R3tWOUdkZSHOB8lY7y2c5XycXdXJyrLylS+5u9G+NnV2QE7dRg4Xy8tLarrWu7jNa4fOXxVLpcqMyuUJ7XKatxGZWVhfkHVZVZzJTopvFymV+lvJWtrVNYWFubQHGqE2+nAyMiwuqblNl7j++fmZhH0+WCtrFTlkOsirTiK1zgt2M9QUyPVj3WYpnYiEi/a7uO1Ueoscvq4qT7jz3rTnI3Dxm2NbDDYA7oCawYe3aFgrbqaKrhyNXJhhJaXltFKGbKGYG1+zpgGcYYqdj/DmsuNyfHorlWd4pGVDVjjeDBCt+XoDoJKhrVQfQM1apHTsPWKRxIZ1tpbWhUY6RZ50U8A6KLKrb21RVVOesXP2tnecRXW1vSHkxsHObpje+ja3aAG5EHS7dkN2h3ZDdrKu0H152ueAmO/PAQDA1RmjNAS1bm809BmNqs2wggtU8ewlTrdDC3jBtW5i4uLqPEHYTdbMTI8Er2qTwtUd/Ozcz1u3G7QcXjdHnicvBvUmGfnsIUbZTfontDthjXeYWqEeMcdZ0iGNR4VMkLTm2DNsMKzw2CtiWDNiLUODGcbsNZGsMY9Ub1iP3m0jmGtjWCNRyT0SjVqBGtOBWtdAmu7THv1nDU1Ykx+MaxxB8eIcC4uLqE5CmvdFF4j/ORRxJbmkIK1MYPOGmOwqvYHKJwWam+GDQknl2M5Z21rJbAWQwJrAmsCa/oksLZ9JLAmsGZEOAXWtl4CazEksCawZhSs8VljOwXWItOgAmu7TQJrAmtGhFNgbeslsBZDAmsCa3sX1oxp0AXWto8E1gTWjAinwNrWS2AthgTWBNaMgrWdNA0qI2u7UwJrAmtGhFNgbeslsBZDAmsCa3sR1mTN2u6UwJrAmhHhFFjbegmsxZDAmsCawJo+CaxtHwmsCawZEU6Bta2XwFoMCawJrBkFa7JmTWDtTktgTWDNiHAKrG29BNZiSGBNYM0oWNtJI2sCa7tTAmsCa0aEU2Bt6yWwFkMCawJrexHWZBp0d0pgTWDNiHAKrG29BNZiSGBNYM0oWNtJ06ACa7tTAmsCa0aEU2Bt6yWwFkMCawJrexHW5OiO3SmBNYE1I8IpsLb1EliLIYE1gTWjYG0nTYPKmrXdKYE1gTUjwimwtvUSWIshgTWBtb0LazKyttsksCawZkQ4Bda2XgJrMXQF1mpqMTZqTAZaWlwk/2pgLqvAyPBw9Ko+cThbwy0EgTWGNYgz09MI+HxUgNyYnJiIXtWnSCEPqQLE8WCEesbCOGthWPsUk3PGxCdDpbfKo6CSYcMIDfb3q7Vg7QY1aiyeWnU7nWhvYwDUH05+1s6OTrjsTnR3dlPLGf1BhxhMhwYHBda2gTZgrZfggjJh9Ko+9fX0KFhrb2uPXtEvBkCnza7yjBHlT3VCyC8vQRB3mozQ8tIywlSX2QnWuI0wQivLS2glWGOoHB8zpoO8SPVsTRTWRoZHolf1iQEwHApRx7sRc9SxNUI8IOCtqqJnN3BwgMIWFljbG1Kw1tmF6kAAfb19KuNzRk3WFhcWMTUxiYDXh7ISE3qpouNRMS238RqHaXpqGo11DfB7fKqQ6w/nggJJ7uVwD3dwcEiFXcttIjZOhZDBl6GS40FPODfC09pXh1MV+5Dm/AiDYxSf1OO93m0ixunBceiwO9RIJffO9IaTIaWzowPWCjNC1COdm5tVcazlPh7j8LCfHe3tsFms0UpTbzgX1LOGQ82wVVqo0WjB/Ny8bj+5wuSRBx79mzdo1FeUnBjWeFS/vcWAtN3Ig62tKC8tVSPm/N0IP9vIT0tFpfJTb/ljmyY/QgQXToKgNsqL03RtdmkxaZsjqBqnzmxdfQMqCdZa2tswS37OUTiTNvJ3cnYa9U0NcDgd6BsYwDzVRZpu4zXyc2xyEh6vF2aqe3p7erEwrx1H8RqnBXfe6+vqVD0+NjqqO30WKM0HuDNrt8NhtdHnAd1+ct3DYWuoq4/Cmv4R2jspgbUYYljraG2DuawcNspEQeqhBH06jO73uD0oyMtHWspl1dBWB4LabuM18tPn8cJUXIrC3ALVMzEinC6HE3nZucjOyKJC5KDr/hvdJWLkJ0+plhQWobigEF53FYJ6n53MZM/DpznP4XjBm3C4K1Htr9Z0F69xejCkZmdmoYjC6ae41RufAb9fVZaZaRkE6aVqxJKnJrTcxmXqXvazElkZmcpPDqceP/lehv3y0jJkpWeioqyMOhV+fX6ScbgcVqsaTTZqil6UnKao4ea8bS6voDxI5VlnHlT5mvxKS72sOp9G+VlB9W1mWvqVfK3LTzIvlbcypx0ZNgsKa3wwhxthbmnSZRWheuR6XUi1VaAw6IWluREW8jdpY3/JzzyPC+m2SpjqArDSNU23cRuFs6kOWXaqe4qKYLfZKT701+M8XVlaVIxiqss5P+mqy9gozRnScjKzI+0NhVOvn3w/h81aaVYzOSsCa7tbDGu81mEjY1oo4fVahakMmZfTceHseYKWIljNFk138Zq10oLKsgrkZmUjg/wtN5nUNS23iRhXlGkpqUi9mILS4hJNN4laeamJCmOmMo4HLkha7uKzyDPmlFzC+xlP4rOsv6KkLI/8tF7nLjHj9CijcPJzZ6VnoJIaI33hjFhhXgEuXbio0okbOC03iVklQX8BUiicuVk5yk+94WQ/GNBTLlxCfk6ugkEtd4kYr800Uf7hSl5g7c6KYY0bwiLqLBqRtmyF5NeFc+eRm0150CA/C3LzcOk8l5VIvtZyk4iVmSuRbq3AGZcZqQE3cmp9yK3167LsGi8u+pw4QX6ecVvps0N912UeB84QqJ00m3DebdN2k6Cd89jxjbUc50qpDaM6l0csteIoEeO6O4fqMQYrrtONqB+5jb18Kdre0Gcj2jAOG9c9PPNgxNrHOymBtRhiWOvu7FK9u462dkxMTGBiXIfR/bx+h4mfR5h4uH9yYlLbbZzG9/NGhZpAEG6HE/39/br9ZOvt7lG9Hc70XRQHWm4Stf6+fvipZ+f3+lQ88HC6lrv4LPKMDe0+fGN6DSm299DV12JIfHI4uQLiEUveWKIvnBNqWpXXePCoVU0wMnWg5S5uo/CwnzylyjDJ0xGjoyO6wzk6MoK62jo1stFQ10B/Y0x3nmc/W1taEG5uFli7w2JY4yUdofoGtQZXV9pu5EFqCLku4zzI3zXdxmtRP3nhOnc666prVfnTlwfH0TM0AEuoHlkEWFWdLegeH0H/5Lguax8dgrW1Cal+F/LqA7DQZ2tbSJdVhhqQ67QjrawUptogrO3a7uI1S2sIJU21CgJzvC60dnUZkka8YYhHw3gDGm9y0lvvcBp18TIRBjSCSV4yYkQbxmHjdpGXdsjI2i6XWrPW1Y36mlqVyY3Q8vISNYg1qsfIDZkRWlldVbsMaymcPF9vhHitSGSDQZWq5I3QwiIvTG1WC3M5HoxQ73gLzln2I9vzKabmjYlPXjfDGwx4+NyozQBcwfEGA4Z+o8TrPHiDQUd7G33TH841elYGc95g0NPVE72qX9yZ6GxvV/EqunPiNWsNdXXo6zZmQTyLd1daKirULmKjxJsWeP0S5xnOk3o1s7QAT2crChuqERrqw9IKLzZfT/4/CtPs4iKqezqRWe1BWagOQfoc7E3eqvu64KMwlroIrEwlcDbV0bVuTbeJmJ2g7TIBZVG1D8OTxmwU4/VkLdT54h2hRq1DZeDjOpeX8fBnI8Rh47ZGNhjsAW3AmhzdIUd36BFX7vIid9kNeqe1N4/uWMfUwhzcHS0oaAgSrPUrWFtfX9Nh65ihjucGrJkI1gIaoJSIXQ9rDgVrXZpuEzF7WzPSCNYKq70YHB9TsKlXXI7l6I6tlcBaDAmsCawZBWsDcs6awNodlsCawJoRaSSwtvUSWIshgTWBtb0Ia/Ju0N0pgTWBNSPSSGBt6yWwFkMCawJrAmv6JLC2fSSwJrBmRBoJrG29BNZiSGBNYM0oWJM1awJrd1oCa3sc1giCjEgjgbWtl8BaDAmsCawZBWs7aWRN1qztTgmsyciaEWkksLb1EliLIYE1gbW9CGsyDbo7JbAmsGZEGgmsbb0E1mJIYE1gzShY23nToAJru00CawJrRqSRwNrWS2AthgTWBNYE1vRJYG37SGBNYM2INBJY23oJrMWQwJrAmlGwtpOmQQXWdqcE1gTWjEgjgbWtl8BaDAmsCaztRViTNWu7UwJrAmtGpJHA2tZLYC2GBNYE1gTW9ElgbftIYE1gzYg0EljbegmsxZDAmsCaUbAma9YE1u60BNYE1oxII4G1rZfAWgwJrAms7V1YM6ZBF1jbPhJY2+OwRhBkRBoJrG29BNZiSGBNYM0oWJNpUIG1Oy2BNRlZMyKNBNa2XgJrMbQZ1sZGjYG1pcVF1NXURGBteDh6VZ84nC3hMEFgDebnjGkQZ6anEfD5qAARrE1MRK/qU6SQhwjWmlQ8GKGe0TDOEaxlE6xNzhkDawyV3iqCNaqMGDaM0EBfv4KgdoMaNRaP1rmcTmooGQD1h5OftbOjAy6bk2Ctm9s53WIwFVjbHtqAtV6CIcqE0av61BeFNc7XRqmH/HTa7CrPGFH+phfmURWFtebhfiwzAPLz67BZhrXeLmTWEKw11yswYrjSY36GNXcE1pyhetT0d2u6i9eCfQRr7ZtgbcKYTvcCdbTDIarHGxsxRx1bIzRBIOklWPPw4MCYMeGcnZ1BmNobgbU9oA1YqwkGMTQ4qCoO7ukla3w/j9pUB4KoMJVhoL9fNWZabuM19nOeR6yopxP0BzA9Na0/nGQ8msbA4nY4MDIyottPtunpKTTWN1CDUa96PXr8XF3he1fRMdSAM+Z9yHB9gtGpfqzqjE9OD27U3A6nath4BFBXOOlelY+oAbKZrariWCRQNcLPbjUCYUe4uVl3ONnYj9aWFtitNrS3tdPfWNLvJz1rf08vNbytAmt3WJyvuaPY2c5pu3zrtF3WuLbJruRBgvvKsjLK182x/Yxhyk/6l0d37WaL6oAuEBTpzYPjM9NwtoeRWxdALQHM5Pwswda8LhuZnYK3qw0Z1VUwNdXCR5/9Xe1JW6C7HZ62ZpQ47cgqLYa9oZaudWi6jdc4TJaWRqT6XCgIeNE3OqwZP4kYpwXX3dyRra+rw+TkpO70YRsZHoabOp4uu1N9NsJPDhuHU2BtD4gTuIMaLUtFJZx2B2praslqrrVqje/XX9uw2hr4fX4UFxYi/XKa8rOOgOAGd7fyY8Oiv9eRn0F/EOWmchQVFMLn9Ub8vP5+LT9v8Z2HpPNz85CXnaOmQrXcJGo+rw9lJSaYiksRoHio4/jUCsMtwnX1eyTeKlwF+DT3eRwvfAtun4WevS4BP278znHn9XiQS89dWlxMYB24Gs7r77neNH6viZrdYkV2RhYqyspRTfB/vbtEjf20WizIycpWftZQB0AzLyVgHK7KigpkZ2XBTHm+prpa010iFiQ/efSvnj4b1QsXJacparw8Lhd1GizXpq2OvG2jPJiRlo6K8orYfmy2691Gv7OfFrOZykomQWCFyj/Xu7nm++Zr13+PXvNQ2cjzunDB41DAZiaAsbY26bKKcAOyqr046zAj3VKBQqtFt+VXViIlJwfnU1ORXVqi6SYRKyDLslbirKUMKZZK2L2ea+MmSeM2rLy0DKUlpfBRXanqRw138Vst3JQv87JzVb3L7Y3euozT3Vflhc1qVQMZ3PnYyRJYiyGGNZ5iKi0qRjGBkKXcDHN5pYI3Nv68+fvNrm2YlQojj6hlpKXhwtnz5GcRXTPf4O5WfmzYxu/sZyWBWk5mDjIup1MhMik/tfzQ+r752ubPDFSXU1KRejFFPb+Wm0StrKSMwpmFHIKWSooHS8W18cmmFaZbfc8pvoQP0p/C51mvoKQsF9YKyzW/a92zcU3rO8ddGcVhCj13ZnqGajCs0XBef8/1dr2bzZ8L8wpw6fxFgqscVFLDtnE9GbOqfytQkJePlAuXIn4SsHFe0HIfr7EfXGGmXLyE/JxcAjZ+dm238VplGVXqBL0M5wJrd1YMazy9WET5xrwpD8abt7WuF5JfF85dQA7lm1h+bLbr/+bm7/m5ubhIZSWXOiKcJze72fi88f1mfly5RlZG5SLNWoFTTjPOVNlw0WPHRa9Dl50nf07bynGyNB8XC/KQXpCP9HwdRvdfps7x2ZQUnDx7DpeontTrZxrZpaJCnCwrxjmyIiqLHB+b4ydR4/qAQS0nMxtZBNTlBGx66wiuy7iN2dze6K3L2E8OWxkZT9fySNtOlsBaDKlh/s4u1dDw7riZ6Rk1zZis8f2jwyNqepEbsM72Dswa4OfY6Jjq3fBo2PDgkP5wkvEUrcvuUL3w3p4etYZNy228xn5y2HgEqJrik+NBTzjZP/431BWkyugNXLa/j97BNsxO6Xt2To+hgSHYLDYEKZw8Haw3Pqcmp9AWblGQpqYOJiai8TmVlM1M07/U8PLwPgNvfW1dNJz6/GQ/eNqAK3TeBDKlwqntPl5jP3ntUVtLi5quF9058TRobbAa4aYmStvJaH5JztS9lK9bmkNUl5VQvq6n65yPbnQbr6kyTX5y+BjSGq/J18naFPpHhmFtbkRasArFDTWwtTTps9YQLE11yHVYcZlgqLTKBXe4CW76LWkjPx1N9Si0mpFRWABztU9d03Qbp7nIKhprkUJwmutzob23W8Xv5vKZqHF9wNOUvJkt6Per9ah66p0N440qPPtgrbSAlx7p9ZPvH6Kw8bS/TIPuAXECc8apJxBiIDJCGxsMeNSCM70R4nUerQQDPPRr1LogzuwMqQyADBdG6OoGA94NatAGg7EwzlneQrbnU0zOGROfkQ0GHhXOVQMW7rMYfnnau53AxSipDQaO6AaDdQOO2VhbQ2dnp/KTOylGaG19Xa33lA0Gd15Xd4Mak7Ys7sgx3BuZr7nh5t2gnGeM2Dk9vTgPT2cbsmv9sLaFNBfjJ2T93WozgMntQGZhISxBP6p1bjDgzQT+rjaYCPxyykoN2WDA5mgPqw0GRTU+DBm1wWDxdmww4DXSHlQ5jdtgwGGTDQZ7RBuwdluO7ijfAUd3eHyRwkMFyQhtHN3BR2IszO/Bc9Zs9ujOTeOO7mAA5E0Bhh3d0dGh/JRz1nafNmCt26C05TzIG2d4xJjztRG7nJWfXV1qlIWP7uDNTvoUObqjqqNVwZqltemG4y0SNoIgX0eL2rnJsGYO+BDs6dB2G6cxWKmjO6K7Qffq0R1uhwvjBg2MyNEde0h7HdYCXoK123DOmsCawJpo67WTYM1hjcCa/vK302DNKbAmsHaDBNZiSGBNYE1gTZ8E1raPBNYE1oxII4G1rZfAWgztdVjz7wJYW6f/ZpemMbM0GXdFJbAmsLYbJbAmsGZEGgmsbb0E1mJoz8PaDl+ztrAyB3tXAT50PoV3bY+iKHwe04uxn2VPw9qV100JrO027RRY48Oe1Zq1FlmzpuU2EbsG1giIjEgjgbWtl8BaDO11WNvJ06DLa0twEKi9a3sM52rexcXaD/Gu/VF4+8qjLm4uGVkTWNuNkpE1GVkzIo0E1rZeAmsxJLC2c2Gtd6oNX1S9gtS6T7G8uoimYS/esf0FFe0Z9OutKyyBNYG13SiBNYE1I9JIYG3rJbAWQwJrOxPW+Mwxb28FDpofQHrdZ/DT5y+qXsY71kfQOlaj3NxKAmsCa7tRAmsCa0akkcDa1ktgLYb2OqypDQY7cM3a8uoSzB1ZeKX0buyvuB+fVb2IC7Xvo3HIg5XV2IfxCqwJrO1G7SRY4zVrbXtyzZrAmsDajRJYiyGBtZ0Jaytry7B15OCI5SGUt6VidK4PA9MdaB2uxvRC7GcRWBNY243aabC2NzcYCKwJrN0ogbUY2uuwtnPXrK2jcdiL922PIqPhc4RHAkirO4rU2o8xMtcfdXNzCawJrO1GyTSowJoRaSSwtvUSWIshgbWdu8FgZnEC+U2n8FbF79XatRP+t9A44sXqWuzKX2BNYG03SmBNYM2INBJY23oJrMWQwNrOhTXW0vIceiZb0DZWf/V8tTjqKoE1gbXdKIE1gTUj0khgbeslsBZDex3WduWL3OOorPY0rPGhuAJru1KywUBgjd/oolcCa1svgbUYkpG1nT2ypsQNCDdMa/FXUjKyJrC2GyUjawJrRqSRwNrWS2AthjbD2phBGWhpcRF1NTUK1kaGh6NX9YnD2RpuIQisMaxBnJmeRtDnR5XbjcmJiehVfYoU8hBCDY0ErbGP0IhHPWPhK7A2OWdMfDJUeqni4HAybBihgf5+BWvtBC1GVJgsBkAGqwgA6g8nP2tnZ6fys7uzi1vO6C/Ji8F0aHBQYG0baAPWejhtDVJvTw/MFZUqXxulXgJAp82m8owR5W96cR6ezjYFa9a2kIIgXdbfDb8CqwisWYJ+VBMYabqN02rYz662K7DmDNWra1puEzFHezgCazVeDE0Y0+leWFhAOET1eGMj5qhja4R4QMBb5YnM5IwZNDhAYQtTeyOwtgcUgbUu1AarMTQ0pBqeNao8kja6f35uFtWBAMrLyjAw0K8abk238Rr5uRCFoKA/gGmCLN3hJGNA81HhcTmcGB0Z0XSTqDEANtY3oKG2ThUkfeGM3Ns53IjTlW8i3fUhRqcoPtf0xSenB8eh2+lS4WS41hVOupencrhR46mdlnCk4tB0G69F/eSOhMNqR7i5GctLOsNJxs/aRg2kw8oNZTtWOJx6/VxaUlDJjbnA2p0Vwxp3FDta21Ra86gVp3FSRvcuU9p2dnSg3FRGjTfnwSVD/Oxob4fNbFb5mus2XX6Sjc1MwdkWRmaND5XhengJtHRZVyvcrU0ocdkUrFV4q+DtaNF2G6f5lJ8hFLvsyCZYszVU07U2TbfxWwvMLY1I9bmQH/Sgb2SI6h5KI404itsoLbh+bGxoUODP7YTe9OH6kGeZuK3h9xIPDw7p9pNtkgCQZ0cE1vaAVlYisOay29VIS1N9vW7jKdDyklLkZGbB43aroWQtd4lYHflpod6tqbgENQSCWm4SNR5VKyksQlF+Afwer6abRI3DxiOKlQSqHA9abhI1u8eE43n7cb74ffiDToTqGzXdxWshSg+G6UJ67kpqhBqoQtJyl4g11tXDTRVRfk4eNUIWNNQZ4Wcd5UsHCnLzYa00GxJO9oOBsiA3T01DNdDf0HKXiNXX1FKPOTKlPD9vzBS9KDlNTk5SnnFSPVEKp8NBHRKnLuPGtbSoBCkXU6ieKFTftdwlYuxHSVExLl9KRWFBoRrl1XKXiNnoWbMdFpx3VCDVWYFMp5msUoeRH3byq7IYF0sLkGYuRSb5re02XqtABoeP/LxUVoB0W5mGm8TtMtlZCt/lshKYLWaqhyg+OZ10mI3qhoK8fORTPWGl+kzLTaJmLqf4u5yO9NQ09bmK007DXfzmUPViBbU1oaYmBW87WQJrMcSjCtxzCDeHqAEPqmlG/VaNoN+vAKjGSD99AXWILY8CartJzHj9W4CALeDzqc9abhI39tOnjD9ru0nMgtU+uP1mVPltqKkxJj75eTku+fm1fk/GOP+wnzz6qfV7MsZQyesKjfZThTNgzLNzXNYRsPX19Oz4CnOna0rBmkPBmosbQ5eLYCZJi97LHcTUi5dQRGDl2nQ9KYveW0p+Xk5JVX46ueHV6Sc/a2VlGQoyU5F/8QyKctJgqiiCyVKKUnNJUlZCUJVTmo/0gmzkm/JRSt+13CVi7Gcu+ZlZlIPC8kJNN3GZpQQmczGK8zOQf+EUssnysjIUvLidbl3Ga5h55J07swxsNurc8TUtt/GbC5YKAuj0TGSkpROsVZKfVRruEjGXChuvp+R10jxSt5MlsJaAeHrMSKP/3XBt29qaxrVtZLzBSf1z3XU9dnvS3Hg/b4fR/264ptdEd15qzVpNDbo7OtQUNUsrreIxFndme7u61Eh5G29yoe8sLffxGGuN/uX1ko7obtCN6Sst93EZ3bu4uIiuxgZ4T59G4K39CH/wIXqzMzDktGDEbcOIK0Gje/odZlQX5MF8ORWNpYUY1nKXoA3YzaghPx0Z6WgnuBxNMmzDLiv6CnPR8snHqN//FhyffQZncbGaauT41WMcn/Nzc1c2GPDSFpaW20RsbHSUwNqtRlbHopv5tNwlYjxdy6Am06AikUgk2jG6usGgUwG5Eerr6Ya5vBztrcZtMFBrMW02tc7RiA0GPKrCO0td+QVoOH4CnYfeRt/Hn2KyuAALfg8Wa/1YrPbFbUs1Pkz7qtBYUgxLehqBVTkWgtpu47WlGj9m/FVoKi2GKzsLgw6ruqbl9qZG7jkcU+Wl6Pv8M3QdOISeixfhLSqC3UxgOjwSjRF9uj0bDK7uBjVyg4HsBhWJRCLRjtJmWDPq6A7eucmw1kawxt/1iv1QR3cwrMVxdAfv3G4ld7W1NWrXsZZ40wKP0lU5nOj0+zCck42uw2+j58OPMFlEwBbwYIFBh4AnHlu8BtbS0RaFNS238RqD1jTBWmMU1gYI1hR8abjVtKjbqbIS9H5yFO1vvIXhjHRMdXWi2h9QU4LDQ8OGpJEc3bH1ElgTiUSiPaLdBGu8y9hiseC5Z5/F3T//GX7w/e/hvt/9FsXFRTeMxm3AGsMAr51cHOjDWEEBut5+F70ff0LAlo/5BIBt28Eau6PwT5qK0ffJJ+jcf4BALQPLA/1qNy2vjeaRNYG1nSuBNZFIJNoj2i2wxmvQ8vLy8Nvf/AaPPfoozp8/h3NnzyhY+8P9v0dNTU3UZURXYM3lRn9fP9YJ5laGhzBGYNf17vvo+ehjTBTGD2zbC9bIDbnjqc9eArWOt/ZjhO5fHhrgyFRTljyypqZBBdZ2rATWRCKRaI9ot8BaY2MD/vD7+/DEY4+pkbINlZtK8Yuf3YWvv/6KPIpeJF0Da719V35aHh7EKEFfx8Ej6Pn4E0wUF8YFbNsG1uj3+WovpirL0PfZ52h/8y0MU3iWBwnUohJYE1gTiUQi0Q7SboA1bnQzCEjuJihLv3w5ejWi+vp6PPTgn/D2kcPXvFP0BljbCCcf2tzXi5GcnMiU6EcEbDzCRtB0K2DbNrAW9GKS16gdPYqOtw6qNWpLA/28TTfyfKTNsCbToDtXAmsikUi0R7QbYG18fBzvvH0EfyYo43fiblYoFFLTogf2v6Xe0LChm8Iai+JhaWgAY4WF6Dz8Dno+/FCtYWMQuhmw3XFYo7/P/06ZigkwP46MqPEaNZ76vE4ysiawJhKJRKIdpN0Aa/yO3ZdfehHPPfM0xsYi53FtiEfWHn74z3jv3XfiG1nbEH1fHhpUwMZr2Ho/5WM9eA2b9gjbHYU1BjUCyamyUhXOjrcOYERjRG1DAmsCayKRSCTaQdoNsNbX24sXnn0GL73wPCYmJqJXI3K5XLjvvvvwzfFv1CaCDcWENRbFx/LQEEZ5hO3td9Dz0UeY4BE2jTVsdwzW+Dv97akKE4HaUXTsewsjmZmRNWrr2ukpsCawJhKJRKIdpN0ysvbSC8/h6aeexBg18BviHaKnT53C7+/7nTrSY7PigjUWXV/q78NITjY6Dh1B7yefam46uCOwRp/nA97IgbdqM8F+DKelEaj1RwOvLVmzJrAmEolEoh2k3QBrE9E1a/f//j7U19VFr17dXPDaq6+qhl8pGp64YY20Tn+PgW2Uz2FTx3p8hPHCvGumRLcc1njqs9qLydIidS5c5/6DGM7MwNItRtQ2JLAmsCYSiUSiHaTdAGu8Fq2ksBA//uEP8eQTjyMjIwNnz57FE48/pmDN6XRGHHJYos+YCKwp0e/LfA5bURG6jvCU6Meb3nQQBautgrUosEXOUfsUHW/uxwg989KQ9tsarpdMgwqsiUQikWgHaTfAGotH186ePo1f33sv7r775/jhD76P7333O8jLzYm6IPHzRcOTMKyx6P7lQd50UICud95XoMTAxsd6LNYGtgbWaiOgNhmd+uw8cFitUVObCeKMa4E1gTWRSCQS7SDtFlhjrRCA8fq19vZ2FBJQ8ZsLnnn6Kfi8XgVnm2EmKVhjra2qxfsjebno5HeJ8psOeIQt6MV0wHN7Yc1pUy9nVyNqn32mRtT4HDWt4zluJYE1gTWRSCQS7SDtJljbrLXVVVjMlXjisUdx5PBhDF/3QvekYY1F8bTY1xcBtk3vEp3yOAmsSm4TrGVjwGbGNL/r8yiB2oFDajMBr6VLVLJmTWBNJBKJRDtIuxLW+G+yra5haGAAnR3t6iXvm6UL1lirK2rXpVrD9t4HBGwfYzgvGw1FBbBmZBgOa86sTHRlZ6KP16jtP4SRrKxbHs9xKwmsCayJRCKRaAdpA9Z6CYaMEr+b01JRgfa29ugV/WIAdNrt6Ghrw5oBUMmbEtoJJr0EAwN9tz7q4lZaGxnGRHERet57Hx0ffojA2TMwp6WhzVyhNgLwGrOkrS6A6YAXTQRr9tOn0fzBR+g+eASjmVlY2fSuz0TF4FoTCMJhsWJs5NpDhJMVH5MSDoUQamzE/Nxc9Ko+TU5MwFvlQZXTjcnxa8/PS1YctnBTSGBNJBKJRDtHDGt1NTXoaG3F4sKCasj1GDfaDFTlpaVoDjWr71ruEjH2g8HKajYrIJijBlfLnabx31+I2uLV62qEhRptl92Bro7O5MO5MI+Zrg70Z2ai+cAhePfth/OLL9CWm43pynLM6DFLBcbLTWi9dBE+8rvx9bfQn5qCmc4O+rvJpxWnud/jhaW8Qo0qGpFGk+RnQ12dykv8+i8tN4na0OAgnA4HHFY7hgYGNd0kauNj42isqxdYE4lEItHO0dTkJJwELMUFhbCZrbBTw2i3JGnRe4sLC3Hp/AUU5ObTd9u1bhI15acNRfmFSLmYgnzy02q2JBBO/vtk9GwOsw2OaHgslRbk5eQhLSWNwlscdad1fwzjcJBflows2N//EN4XXkbNC6+gef9BdB55W21CSNqOvIOOw0fQ/Po+BJ9/GfYj79LfyaS/S2FNNp3oPnO5GZlpGRSfF2EqLtF2l4ixn5WVyM3OQU5WDioJAh02vs7hTNasKCs14XJKKlIvpcJUUhb5W2Y9ZkOlqQJlJSY1AhjP2sftLIE1kUgk2iNiWHM7ndSImdSUoM/j0W2VZeXUyF5GKYGAr0rbTaJWXlqG9NR0lBYVq3VmPDKk5S6mRcNTRX6UFpUgm+CHw6s3nAG6v7qiAv4zZ+F/7wM0H/0M3SdOokendR3/Bg2fHkXVsWPwlZTAr8KZ5LNHrcrhRB5BVXrqZVgqKjXdJGZe8jMC/IUE1Txd7fdquUvMbBYLsih9GCytBMQ+t5fyqEeXORWsVqr1dQJrIpFIJNoR4imx2upqtIXDmJ+dVYvPF+bnkzO6d35+Tm0C4FGRUGOTWniu10/+t62lhRrZCjQ1NGJmZkZN2d7gNl6je6enp1X4XDYHOts71FomTbdxGodnmsC3KVgNOwFlR10tlkZHsTw2lryNj2NucBDNPj/clWYM9vXre242up/Xf/kIXMwEqbwWkNNM0228Rn7yOXe89pHz0hg9t+5wkvExLDzq67Da1Gf+O5yfkrWF+QW1Rq+Bp0HDLTINKhKJRKKdIYa1BoM3GPT29MBcUWn4BgNutHntmhEbDFZWV9FB4WNo0bPBYLOWllfQ3ByGlcLZTXFghJYpnAwWPBI4btAi+8WlRbXBwG6xYmR4JHpVnxikNjYYzBH0GyEGQB7x9Liq1GcjxGELh5oF1kQikUi0c7QBa0Ye3dFDYMXrlow+uoPhgo/b4J2cesUNtdoNSiAQObpD/7MvLi6pTQu8pq6bwmvEs/Oi+BaCiyqnC2MGHV/BYMVHd9i28dEdHCI+uoOn5nk3KH82QhsbSwTWRCKRSLRjtFNgjeGHYa1dYE23BNYE1kQikUi0gyQjawJrAms7UwJrIpFItEcksCawJrC2MyWwJhKJRHtEtw3WynYGrPHidYE1gbWdKIE1kUgk2iPaKbB2u9asCawJrO1UCayJRCLRHpFMgwqsCaztTAmsiUQi0R6RwJrAmsDazpTAmkgkEu0RCawJrAms7UwJrIlEItEe0U6Btdu1Zk1gTWBtp0pgTSQSifaIZGRNYE1gbWdKYE0kEon2iATWBNYE1namBNZEIpFoj0hgTWBNYG1nSmBNJBKJ9ohuG6yV7Yw1a3LOmsDaTpXAmkgkEu0RyciawJrA2s6UwJpIJBLtEW3AWi/BRaSJ1K/enh4Fa+1t7dEr+tVLAOiw2hRgra2uRq8mrxUCvg4Kn49gYKCvP3pVn5aWlhEOhWCzWBSwGiEGitbmMDwuBpbx6FV9WlxcRE0gqGBtZHgkelWfGAD52UONjZibnY1e1aeJ8XH4qjxq9JM/GyEOW5jgV2BNJBKJRDtGDGt11dVoIyCYp4ZscX4eC3NzSRnfO0//trW0oKzEhKbGJvVdr5/8b2s4DDMBYKi+AbNT07r8XJifwzQ9N4OF02ZHJ0EbP7um2ziNwzM9OYH6mlpUlJWr8M7PGeHnJMF0nQLVgd4+fc9NxvdPjo0pSK2kcPZ0dWu6S8TYzwkCyXqC/ppgEGMEgHrDuTA7p56X04effZCAepGAcIH91WGjIyMqPsOU3wXWRCKRSLQjNDMzg9pgNTwOF+qra9FQU6fbXHYnCnLy1bRlA8GLlpvErBZOuwNF+QXkp4XgskY1uNpu4zC6t46emcNnKiqBm59dbzjJz1oCFUtFJQopnE673RA/OZy2SjNKi4rVKJOu545ajT+IitIyFFM4ecROdzjJqslPK4WTgTro8xsQzlr46Xk5fUoKi+H3eNFQ10D+1usynv7lZ+Ypeh5d3ckSWBOJRKI9Ih5dGBoaUo0XG08zsl3/Wev3m31vDbeiOdSsRpeu//1m92y+pvW9NdwS9bPlht8333P9941r139va4n4ySMsHN5k/Lj+O1sL+dfcHJlm2+xm4/fr74n1nW3Dz9aWSDg3u9v8fePzzX6/8p384ecOs59xhDOWXesnxWc0nNe7ifX9hmtRP5vJ+HN7a3vE2qJ2/feNazf53kaf2bo7uzA1OWnIWr07KYE1kUgk2kPiRmttfQ1ra8bY+tq68pM3LGj9noyxXxE/KazX/ZasKb/42Q31MxJOI/1kMzqN2K/bEU5DjZ+X01yF87rfdBj7R/+L5v6dK4E1kUgkEolEom0sgTWRSCQSiUSibSyBNZFIJBKJRKJtLIE1kUgkEolEom0sgTWRSCQSiUSibSyBNZFIJBKJRKJtLIE1kUgkEolEom0sgTWRSCQSiUSibSyBNZFIJBKJRKJtLIE1kUgkEolEom0sgTWRSCQSiUSibSyBNZFIJBKJRKJtLIE1kUgkEolEom0sgTWRSCQSiUSibSyBNZFIJBKJRKJtLIE1kUgkEolEom0sgTWRSCQSiUSibSyBNZFIJBKJRKJtLIE1kUgkEolEom0sgTWRSCQSiUSibSyBNZFIJBKJRKJtLIE1kUgkEolEom0sgTWRSCQSiUSibSyBtVhaX8fqygrm52cxOzON2dkZQ2xmegrTZDNG+TkzQ/5NKz8NCyf5M0N+cliNDGfET/KPPmu6SdT42aeifmr9noxdeXYOZzSsOmwmapE00u/fhnG6cJob6SfbwsI8VldXo4VAtFu0vraGpaUlzM/Nk80ZYnNs0TKjWZaSsEjZM77emZ7aKCvG+Kv85HCynxq/J2P83FMUzttW57JFf5ubnY2kXaJGYbvShm321wBTYbouj+mxhYUF1YbvdAmsxdDa2irGRkbQWFeHoM+Puuoa3VYbDMJXVQW3w2Gsnx4PPG43auizlptErSYQhJf887jcqPYHNN0kajXBanp2j3p+/qzlJhGrJeOwVVEYPe4qFQ9a7hKx+prIs1c5XfByOKur6e/oN7/Xp/z0ebzkZ1DTTaIW8HnJT6dKe053LTeJWnUggFBTCJOTk9RXWY+WBNFu0OLiIjrbOyiP16Khrt4Q43LMZY/zt1Z5StQ4D/q9kXzt93rUdy13iRiXDT+VEbfLhYBB4VR1GftJZTpA4TUinOrZyU+uJ4yrc6kep3qsip692s/tTSScfD3gd5NxHHPdoX2/lvG9XI+zv1xfcLj1GNexQXpe9tNP9WMd1cEN1ObqtfraOjQ1NGJkaIja8rVoKdiZEliLoZXlZXR3dsJps6tGtpkaMW7IkjW+v4EyUHlpGXIys1TmDIeaNd3Ga810f2N9PWxmK8rI31qqiPmaltt4jcNZE6iGqagExQWFqiBpuUvUOGzm8kqyClWQ9MYnW5AqoMK8fJQWl1ABrdf97OHmZqpAalCUX4DKsnIVt80h/q1Jl3FlWZCbB5vFpiqQZg038Rrf29TUqCr1gvx82KxWNDY06A5nE/mhGiCHE329fQJru0w8qhTw+eChfBNqpHxEZYXzTDIWqbeaVR7MzcqG3WJVeUhPmY7c2wSX3Yn8nFzYKV9zntTrZyPVC3Yqd1yXcceOn13LbbzGfnJdY6k0Iy87l8LroOs6/aQ4jdTjZhQVFMBPHXkj6nGuZ8tKTCjIyYOf2ht1nf6Wz+9AtukU8isvorrGR27j+1sbfvKzc13OoKWnLlPW2Ej50o/iwiJ69iJVp3M9vDm/JWphCmctQR/XZWH6vrLDR9cE1mJomWCtp6tLjbQMRemcp4eSNb5/fnZO9UbKS00Y7B8wxM+F+QVViBiqpqdn9PtJNjk+QT2nSMM9Njqq6S5R47A11jcoYJ2bmaW/oy+cbDzy6bDa4KPe7fzCvCHxyY0a95g5nEuLi/r85Hupoujt6VFA3dIcVvmK41jTfRzG4eHKp6e7Gw6bDS3hZiwvcTi13cdrK0tL6O/tVSOUDGv8d0S7Rzy9xqMWXe3tqiOq8qZGPojLonmwu6MTFSYT5cEWlc/1lGlVzsiPro4O6tRY0BoOq2lbPeWPy9nC/Lwqd1yX9Xb3qHBruY3XODw8lcydLgYWHq3U7ScZh7OZwMVlt2N4eFjXc7Px/TytyKOJ1gqzam9WV9awvLKEpu4qnDMfRHHgFManqW2LM93Yz1nykyGaR684T+mpyzZsdHhE1blOmwMjQ8P68mbUpiYn0UTtDXcsuM7dydpZsEa9/PXZGawSOKxRBqELkeukdWqkV/r7sMyNVkcb1ijTK3HlMT6mDIsLkWsJKAJr3Wrod2yU/DBA3PhzhcmjNiNUII0Qh7OVKkseEZrfeHad4rUI3NvxuqswNTERvapPHDaGyhBVcosLi9Gr+jQ5Pq4q4SABsFEFktdMMKhyOLnQG6GB/n6CSgfaW9sMG7Hq7+ujCs6J9rZWqkT1h5PXNA0NDFB+r1Z+c8Usuj1aZ1iivLs2Nop1ym/rM9TJGuO6iq5xnTVNddz1eY/Sg+u+1dER5Z7rxETEDWt9bS16qQOa6L03Ux91Qszl5ZQH26NX9KuXOiFOApaOtjZDyh+DKZc7rssG+vqjV/VpaWlZQYC10qzaCCO0vLyE1uZmeFwujFNeMEI89c2DDXazhdqbEXVtZmEcZbXn8XXZC3C3FGBxJbE2g9eB8WgVj4gxDBqhCcr3XOdWOdyYGBuPXtUnDhuPsG10kHeydg6sUYFdqg5g4t3DGN/3OhYqy7G+QpUdwc5sdgbG97+B0ScewfADv8PIww9g4oN3sRjwY7WvFzPnzmDs5ecwfeYE1kYSg6PNsDY6Mhq9qk+LlNF5np5hbXhoKHpVn7j3yRmS11EwaBghXozL61B4zRoDkRHisPEUBPd2eDTQCE1QpcbTEAG/X8WDEeKeI6/D4XAaMXzOcMbw47Da0dbCYKUfgtjPvt5euBwOtLW2UBHRH07uIQ8SVAqs3V6tTU5gNjMNY6++iKnjX2IxGFD10+iLz6q6avTFZzD2yvOYOLwf019/ifmKMqxNjCvAmzdXYOzN16guPIIlui8RbcBaT2enAnO94jzIYMWw1mZQJ4T94NkMHjFub201pPwtU73A5Y7rsn6DpvcXF5dUx5NhrbuzyxA/l5YW0UIQxOv1eDbDCDFY8fo3BWtDw1hZpbai34+zlv1IcbyD3rFmCntieSHS6Y4sm+BNAUaI4ZTrXLeDQNWggREOWzO1NwJrW6g1grKJw2+h9x/+BsMP/RHLjfVYbm/D+KH96P/vf0Xv3/9v9P3bP6L/P7+Fvn/+W2Ujf34A8yWFVAmeRN9/fAsDd/0Ac0UFN/ZWbyGBNYE1o2BtQGBNxKJ0W3DYMXTvz9H/b/+E6W++wnJzCCNPPYqev/n/ofcf/wZ9//L36PvXf0DvP/1fsr/BwE++h8lPPsAKpfcSpc3QH36r3Ey8fVCNssUrgbW9C2sOsxWjBGvTc6OoqLuEY6YXYGlIx9wiz1IlJoG1rdfOgLW1VSyUlmDwZz9C//f+C7OXLqhpgukTX6Hv3/9ZAdrEm69iwWrBUsCHmfNnMXjfvej91t9h/LWXIz3R555SMDf28vNY6e6KehxbAmsCawJrIiO1OjykIIvro5FHH8ZKuFnNEIw+96QCtZFHH8Rcdgbmy01Ul53B6FOPReq57/wHZk5/g1VKl+mTX6P/2/+OwXt+hvkKkwLAeCSwtodhzWLF8OAAOobqcN52CGct+9DWH6Qynnj8CqxtvXYErK0ODWLiyEGCr7+niuwhtS5tqa4Oww/ch37qXfJ0wUp7W9Q1FXYCgulT36D/v/4Vw9QDXbBbMX36hIK6wbt/gnlTSdyjawJrAmsCayKjtE7xu2CzYOg3v0Dff/0Lpo8fU53RVWpER599QsHa+Fuvq3VsSuSeR91GX3kRvf/8txj+0++xVFOtpj+Hfk1+/Ns/qBG3tcnJiPsYEljbm7BWo2DNhu6edjiacvBl6bMorT6Dqdn4R2U3S2Bt67UjYG3R54mAGVVukx9/iNWREcwV5queZf93/xMzaalU4V1b8Sw1NWL6m68xk3KBQK4d85XlGPzV3ej7n3/F5GcfY216Oury1hJYE1gTWBMZJd40MPXFp+j/n3/H0G/vxYLVrK6vUpxfhbU3rsJaVLOZ6ej7z3/BwA/+Ry3lWO3pxjgBXN+//ANGn/wLlkKNUZe3lsDaHoW1QFCNrNU1VyHV8R5OVbyKUG8VVpMYVWMJrG29tj+sUYUyV5CHge/9NwZ++G3MZmWohbYzF84oeBv48ffU4ttYWmpswAhValwZjr30nJqKiEcCawJrAmsio7Q6MKDqH16LNvrME1hua41c7++7dmTtunVovJRj4CffxwBPhZ4/Tf70Y+qrL9D3b/+EwV/8FAtOe9TlrSWwtndhzUztpKkqFcdNL6E4eBITs4NRF4lLYG3rte1hbZ0y2szFc2rNBm8QWKBKi4/vmOFpTYa1n9K1aO/0Vlrt7VE7r3r/7n9h5PFHsNLVGf3l1hJYE1gTWBMZJYazkcceJij7Pxh77eUrUMbr0K7A2r7Xbti1Pm+3YYCgrP/bBGunvsHq2ChmUi+i7z+oXqRO7LypOOry1hJY25uwVkuwll+YhjMlh3Cy/K9o6HFSfZE8vAisbb22PazxdOX0ia9VpTT4sx9iwWHFOmXomUvnIrD2o+9ivlSjoqKKiLe5U0mPfB0ZoR7raxFY+0tk3Vs8ElgTWBNYExmlpYZ6jDz8JzWypqBsOrLW7BpY45E1qq82i9fZ9v/gf9D/vf/GbEYa1hcX1JFFff/5LXV9Lj836vLWEljbe7DG7U0w4MeZ9E/xYdbjyPMdw/hM8qNqLIG1rdf2H1mjxn3m7OlID/InP4hMea6tq3UbvDOU135Mn/xGAdxm8bTn9PkzmMvNVlOeq4ODGHv9lQisUc92pasj6vLWElgTWDMK1hh+BNb2ttQRHY8+FFmO8epLav0t65pp0P1vYH3ianlbo7w4+eVRdZTH4D13YcHtJNBax8zlS5F68QffxnyJjKzdSjsK1sjPquhbY4wQHz7u8dvxUeor+Dj3CdR0WKhc6ztoWGBt67X916xRQZ3LSico+zc13M+fscIH5FZj+I/3RXZIPfwAFlwOtdOKxaeAT3zwjqrIGMyWWyih2lrVGhGuDEdlzVpcEliTkTWBNWO10ttz5YiO0WefxEpbZBf7Zljj6dGVboKpuVms9HRj5tIFDP7yLnXUx/jBN7FGddf63Lw6LLfv3yNr1hYdsmbtVtrb06DzsPgL8G7647hoextDk/EfXXUzCaxtvbY/rFEBWLBUqMqKgW3qs0/U1Cjb5NGPVAXGPU4Gt8kP38P08a+oZ/o6Bn70HbVTlI/sWKMEW3TYMPTbe9QBupPsB1Va8UhgTWBNYE1klFbHqSP5ziHVkeRjhRajGwOu7Ab9+/+t4ItnAcYP7cPIE4+odWp8AO7IXx7Eoscdcd/Xi3Fyw3XfyBN/wXJjg7oeSwJrew/WJmdHUeA9iU8LnoK9KQvzS/rhSmBt67X9YY3E68tUb/Rbf6v+5d6put4axuTbB9H/g2+rHmnv3/7/yf7fSIX30x+o3VL8HlFe36HeYvBf/4rBn/8I8yVFVNvJOWuxJLAmsCawZqx4w9RsWqraxT7w/f9Wo2Ysdc7a80+pmYK+b/1dpD77h/+DXp76vPvHmHj7kDpfjRJEuefDv7nzybDGnVTeIR+PBNb2Fqytrq+ifbAGpyv34WTZG2jrq8GqAe8QFljbeu0IWFunhnP6eHTI/5c/VSd7b4inPPnVLdMnj2Pyg3cw+fEHmDl3GotV7iujZwr2nn1SjcKpA3Q741uvxhJYE1gzCtZkzZqIEg3LDXUYfuQB9P3L32H8zVexOjRAHcpFdVjubOolgrkUBXRzeTnqQG/elMAvd98Qv8Cd1+n2fec/1IzDfFmp8jceCaztrTVrMwuTqKxPwftZjyLF9BkGh3oMCafA2tZrR8Aaa9HrwfD9v1E9zgmNc4jWqUCvz8+pnus1o2a8ayrlgto1NXDXD9W7QuMdVWMJrAmsyciayEitz0xj6njkVXkDP/4u5gvyODGjP9K//PFm7Sn9ziNsQw/cp0bdeGbh+rrwVhJY21sjaz2jzThZ8SYOXXwYuWUpGBkeNiScAmtbrx0Da9ybnDl7CkO/vhujTz+ORU+VqrhiiUfRxg/vV+/Q49eyxLuxYEMCawJrAmsio8VvWBl78TkM/ernmPryaNwvY+edoTOplzD0u3vVkpAl6sQmIoG1vQNrq6tL8LYW46O8x/DJpb/CVF6I0eERQ8IpsLb12jGwRjlMvYJlqTqARW+V2iVFLUn0x5uLX/i+6PcquONTv9mfRHQF1mpqMWpAT4e1uLio4M9cXoGRoWsPv0xWy0vLKkPWkr/zc/PRq/o0MzWNgNcfgbWJiehVfeJCHqIKrqmhEQsL1x63kqwmCCQZWBjWjCqQDJVehjWqjBhg9IthrR9OmwPt1GisrxsBQQRrfQxrTmooCQANCCc34EMDAyp/CqzdPq0vL6n3GS+6XViqq1WvoYpHPF26HGpSbyzg5R3qLMkEtBnWEq0LtUV5MAprDFbGiGGtm8qKnfxsw+qK/ny9QvHEZYTLNHeajAGrKKyZLegiuORw6xVDZUszwZqLgIXgRY/Gp/uR7TmKLwqeRXrBCdgIKhnWjEh3Pmg3TFDZ1NhIHVtjYI3rcYa1KqebPhsDa3PUueE0EljbA+IE7qaKzVflUT0zLkDc40nW+P6B/n64qedUUlCI1pYWlUm13MZr7Cc3sEF/AE67Q4226A0nG1eYdosNlopKdHZ0YEyvnxzOnh400LM3VlRgqrEBC22tmG9t0WVD1UFU5ebCV1mJYYqHCQJLzb8fp3F6cBzyc3PlzkDNo3cbv49vsri+870jI1RpNKK8xITaYDVVmhE/N7tNxFR4yE8epawsq1AjtTzFocdPDieHqyXUDJ/Hq+JAYG13aWpyCtVUTzTW12OUDwrnfERpn4xt5Osm8quksEiN6l+5fp3beE3lQfKzgfwsK42UlZGhIV1+sg0NDqKG6gkLAQt3FvlvaLmL1zg8g1TXBHw+mIpL0FBXZ5ifQb9PdeTb29qSem6+Z2RkCFWhUhwreRHnTe+ipDSX6p4ytIZbMDqqP5zc8eRn53qil+p0vqZZpyRgHe0dMFeYySrpc3tSz369cdiqA0ECy2YCdv0jtHdSAmsxxLDWRkBVTGCVl5OLspJS3VZSVIy0lFScO3VG+VlOlZKWu0SslPzMSMtAyqVUFdayUm13iVhRfgFSLlzCpXMXUZiXr+kmLuOwkJVTuOznLsD/zvtofGM/2g8eQefhd3Rb6/7DqHl1H9zvfgBr6mWUU+WpGY44jdOD4/Di+QuUTpcpbvk6p1HyZiJ/87KyceHsOWSmZ1IFr99PttysHFw8ewFZ6RkqD2g9TyLGDQ/nyRL6t6e725ARCNH20eTkJHXArCrfcFpr5YFELYfy9bkz5ygPZmr+nozlZGbh/NnzKl+bivSHs7S4mMpdBpXpS+rZtdwkalyPZ6SlUTjPIieDyrSGm0SN/cxMS8clqnsKkq1zqf7KK8rAF9mv4520v+BcxudIuXiJ6p7zqmwbEc5igvOMy+lIT01DEbc3GnVTosZtzKXzF1W9W5Cro72JmqmkRLVhxYWFaibHiOn0OymBtRhiWOMeDg/z28wWNXoV8PmTtqDfD6/brQriZQIrq9lM5K/XzwB8VVXUWJcgPzdPDaHz39FyG68FyXgdGFds2RlZcNjsmu5iGoWDw+J3OlCVkgLPm/sRePYFhPYfQtenn6L36FHd1v7hR6h9/U14n34eVYeOwJOdjQDFR7JpxenhdrqQRc/NFZG3yqPiQ8ttvMZr/7i3nElAXUqgxj1SLXeJGPtZWV4ZgT9Ke84DQertco83WfN5PGoNDo9A9HT3CqztMjGscd7m+szv9eqqJyL3ch4sx2Xq1DAE8Hc9ZeWKn2XlClq40fVTntRb/rhscIcxJzNbjZhH8ru223iM6xYedecRxYzLaagwmei6Pj+5ruRwmoqKFKzabbaE6zDVFnjcyCw9ibfT/oxTpQdhc5YTCBWocHIbpv/ZI0tjGCyL6Pl5GYaWu4SM6jKH1YZsem6Gfjt9jqT51bopUfP7vGp5jKWyUk2FysjaLhfDGk8H8nD80OAQVtfWsLq6mrytrap5dB6arTCVqSlRnmrSdBun8f2RBZ8hVVin+dBgveEk400FPP3LlTsPKWu5iceWZ2YwVR1Ez9fH0bxvP/wEV/WZGZiocmDBX4V5n1uXDVor4aLerfPgYbS8+RYGzpzBbEsz9aSWkkovjrupqWm4qUJqqK1Tawy13CViXFHw2h6eVub1E7zeRctdIsZ+dlPeZJBuaW7G0uJC9LeVJI3SisLV39tD+T0oa9Z2oXjNGq+/7WxvV+u4uD7anKcSMrqXRyu6OzsIrspUvubvmm7jtaifne0dVFYsaA2HVfnj9Zia7uO0hfk5Fb4qqst4Q8TKCj27hrt4jcvF3Ny8GrFh+Otoi8anhtu4jZ6dw9nc2Ag3QQYva0i0Hmf3Y1MDKPB+jc+KnkRVuBATE6Oo9gXUmrXB/gFD0miG6nRez8vTv1PUAdB0l4hRmHgJBrc1Lhs9+9Bw9LfN9VPixmHjTWKyZm0PaAPW6qprCViMWfS4xBsMaqIbDCiDGiEOJ69HUBsMCNyM0AxBH/d6uAc5leQGA15IPUcFup9ArevQYXR+8w2q09NRW1yISb8HS7V+LOi0QZcd9oxMArZz6P7ic3TvP4ih8xew1N0ZDUXiUhsMCFRDVBlzpWGEeJel2mBg0K45FgMVr39sb2ulitrIDQayG3Q3amODQS8viDcoD/b19BCwlFMebI9e0S8GKqfdThDUZkj5Y5DichfZYNAfvapPS0vL4LVQPFrFbYQRWqb6spU6Xh6CFl6zlajWsYbWgQBOVryGC7ZD6B9vVZsBagJBNf09whsMDNDGBoMQgSUPPhghXivMda7aYDBm0OkDFLawbDDYG7oKa3J0R6JaW5zHbF0t+o4fR8cBAqhzZzBiLkd9STFqiwjWfG4sVvuwoNMGnTY4srLgy8vFeLkJQ9/Q3yNgGzx3Fgsd1IAkUdnL0R0Ca7tRcnTH7j66Y2Z+AmXV5/B58TPq1VILSzPU3iyixh+AnaByeEjOWdupEliLod0Ea+ymmv5uZmYmMjLSYSotVbs8125SePXA2hoV5pnaGgVqXYffJlA7h1mnFRMeF+qLbwOsZRKs5edh2l+FObsZg998g459BzB49hwW2lsTBjaBNYG13SiBtd0Lazyq1jFUjzPmN3HeehDdw010bV21NxuwxtOLRoRTYG3rJbAWQ7sJ1rjwv/H6a/j+976HPz3wAO75xS/wx/vvh91u1yzAycLaGlU4s/V16Pv6ONr3H8DQ2TMEajYs1PhvL6zlMaxFplZnLOXoP3YM7W/uV2vYFjvbqTaLv3ESWBNY240SWNu9sLa0PAdHUxY+K34SlbWXsLAYgSiesuTjWgTWBNZ2tXYTrPH6j6eeeByHDuxXB7PazGY89KcH8NdXXsLQ0GDU1VUlA2v80vzZ+lr0H/8GnQePYPD0KczYzARqEbCa8DhvM6xVYYmgcCHoxVRlmQK2jn37MXjuHBa6OiiA8TVQtwPWGH4E1kR3UgJruxfWhia7cMn+Nk5UvIrWgWD06rWwJtOgO1cCazG0m2DN7/PhyccfQ1pqivrOC3c/+OB9/PH3v0dLuFld26xEYU2NqFFD0H/sawK1Qxg6dxYzDus1YLVlsBb9bcZSgYGvj6sp0QECtkUGtjgaKYE1gbXdKIG1HQBr5GeiL3JfWV2Gv82EL0qeQUnwNGYXJqO/XIU13gghsLZzJbAWQ7sF1rjRLS0twSN/fgiVFRXqGlfcBw7sx2OP/oUqmxt3TiYCa2ozAU998ojagcNqjdqMyxbZsbkJrLYU1tS/fjWyN8Br2N58C4NnzmCBp0RjNFQyDSqwthslsLY7R9ZGp3qQ6f4Yx8teRku/nyMx+otMgwqs7RHtFljj31NTUvCnP9wPn9ejCnBWZiZ+/at78fVXX2GBCt/1ihfW1pYWMMO7Pr/+Gp2HjmDo7Fm1mWBj6nOzbfXImjL6PmOtxAA9Z/vr+zBw7iwWu3lK9OaVlsCawNpulMDa7oO1lbVl1HSYccz0AnK9X2J67tr7BNYE1vaEdgusceH6+tgxfPu//hNPPP4Ynnn6afz0Jz/GKy+/pHaEaikeWONz1GYb6tD3VWSqkdeozTosEVDbRrDG/06by9H/5Zdof2MfBs+ewWIPv3xZWwJrAmu7UQJruw/WxmcGkOv5Ap+XPI2aTjOV2Wt3vgusCaztCe0WWOMTp99791385Ec/xMH9+9VoWlFBvmqYqXRHXV2rWLCmNhPw8RxfbYyoncGM3RwFpE2wtMnuCKxtWNCrdokOHv8a7Twleu5c5OBcjcpL1qwJrO1GCaztrjVrq2sraOhy4KvS53HZ+R5GJm88nHczrMmatZ0rgbUY2i2wNjIygn1vvqFG0rgxjqcRvhWsrfGIWl0ter/8Sh1AO3z+PGZ5jdrNQClqdxTW2AgiZ+2WyDlsbxCwnT0d2SV6XXzIyJrA2m6UwNruGlmbmhtFof8bfFr4GKrCBVheWYz+clUysiawtie0W2AtHA7j2WefxUcfvK+5Pk1LN4O1NR5RU5sJTqDzQGREbZZ3fTIk3WREbcPuOKxFbdZWiYGvv0LbG/vQf4aA7bpz2ATWBNZ2owTWdg+sra+vonWgGifKX8U56370jYajv1wrgTWBtT2h3QJrLpcLDz30IE6fOqka5HikBWvr9Hdm62rQd+wrdB48jCF+afrGGjUNKLretgussfGUaN+Xx9D22psYPHsWS708hRCpyATWBNZ2owTWdg+s8aukzPWX8WnRE7A2pGFhUfsdnQJrAmt7QrsF1jo6OpCTk42mxoboldi6BtYmJhSozdXXof+rr9Hx1kECtdOYsROoMfzsNFiLupkmYBvgNx3wlCifwxbddDBHlZHRsCZr1kR3WgJru2fNWt9YC85aDuC0eZ96tdTNtAFrcs6awNqu1m6BNa6YudJb51E1rqTjKLAK1nwEa24PxgcG1GYCBrUr7/q0X3vgbTy2nUbWNoynRAdPfBMBtrNnsUzANjszDU+VR1VGAmui3SKBtd0xsra0Mg9Xcx4+K3oS5rpULC7fWOdvSDYYCKztCe0WWLtGXFjjKLAbsOamQt5ntaKfz1E7cAjD53gzgR2LBEVsWgB0M9tusKaeodavpnL5HLaO1/dh6Pw5jDXVw0MVZlNDo2GwJtOgojutnQlr8S3buJWWl5Z3Fazxq6VS7e/gm/KX0TFUG72qrWunQUconNEfdGh+fkFgbYslsBZDm2FtzKAMtLS4iLqaGgVrI8PD0av6xOFsDbcQBNaoXo8R4owedLlgP3MWoQ8+QtehtzFMn+fs1gjkMOwkaJObXuQ+5YuAlZa7RGzIab8CazMEa8uJ+qncE7Dxq6mOHUPXm/vRQf8609MRIljj13IZIYYgJ8Fau0GNGouByuV0oL2NAVB/OLkBHxoYEFjbpdqAtV6CIUNabVJfT4+Ctfa29ugV/eohAHTYqKy0tWHVgDzIHa428othoL+vP3pVn5YIAMOhZgVr3EYYoeXlJbQ2NxOsEbAQvGhpVb1aqky9WqowcBxzi1dfLaWlRWpvqgNB2C1WdSqAEZpfJFhrDilYm5vVXiuXqCbGxyOwRs8+MaZ9rmei4rCFBdb2hjiB+VVMQZ8f3VSBcOIzxCRrfD/3mHxVHpiKS9BFfs/PzWm6jdfYzwkq2HVUCfPUHQOg3nCyjQwOIFBRBvPnn6LqvXdRe/JrNBfno81egVZ7JRn/m5iFLGVwFebCWZCDZvrclqQ/m62+ogTlWemw5Gai2VqGdkfifnI4+LlCBdmo/vIzVL1zBJYTx9Ho86r1enrik++dmZ5WowSW8ko01NVjanJS0228tuFna0sLrNRjbqxnP/WFk41HU/mF/wGfD329Amu7TQxrNcEgWpqaMEOfjcjXDBdclzXWN2BmZlq/n7MzaCM/HdSpa6WOyFx7C5a6O7DY1Z60zbSF0UadOr+pFD2tLfR3+O/pCyeP/tQGa1BhKlPQxnGh5TYRU/U4deQZrHp7NNqb2Wn0DrUhzfERjhY+BX9zOf1dSsebPAvfP0l+1joccOfmYbA6QPHRdkP8JGSUFlPhEEIOOxq8Xowa1N4w9NutNtjo2fmzEX4ODQ6qzonA2h4Q93TaqJEtKzWhoqxcUb9e4wyZm5WDlIspys8ql1vTXbzGvTDuhRbmFyKH/LWZrXRNn59sdrsd+aZiXM7PQAZZVmkusssLdFlWWQHSS3KVZdPnLA03iVqmKQ+Xi3JwuTiH/Mu/4m8yxv5lUdjS8tKRXpAJU3kpnBS3LodLpzlhKilFWsplFFE6Oe0ODTeJWsTP9MvpKCoopDxAflK6abuN1xwop8ansqwCvV3dho0AiraHJqmT4KK8x/mG849WuU/U2K/USykoKizS/D0ho7qwymqF69IleN5+F82HjqDr/Q/R88FH6NZh7Ef44BHUHnob1SdPwVtaGv171/39BMxutaMgr4CePRUlRSWGxGekHs9HZlo6Kssr1LWNsul2uOGw25BRdhLvZTyCY7mvodJaoq5fW4ajRs9WZbPBl5WFwAcfo/bNA2ijOO3+4MMb4idR63z3fTRSXPo+/0JBoIvaCn11j1M9b2Y6tTX07Obrnj05c6qObEV5OUKNTYYsZ7mTEliLIYY1fh0TJ3x9XT31dnrQQz2eZI3vb2trpUxkRl5OHurq6tS6Iy238Vpvbw862tspc7thqTSr0Ra+puU2futBiPwsrPbhotuKXI8NJV4HSj12XVbsshAQFRNQFaGE/C31artLxAocFUgvykVmaQGKyU8OZwldT9ooTDn0vBddZpQGPGjraI+kezfFSzJG93Z3daEmEERxQZEa6u/q6lTXNd3HY+xndxeqg0HVUDDwd3Z06g4nh4un/LkD0NvTi/U1gbXdpMmpSfi9XjVTwGneS3UPp3NSpuqtHgQpX+dTg+2pqlLfk/aztw/d4WaE8/NQffAQql98hQDrMLo/+hg9H3+C3iSN72U/mo+8i+ArryHw0l/RcOIE2v0++rvJhZdHnbnOdTmdKCRg86v4JL803MZr7GdnewfV49QJ45HKhga6vlGe+d9e1DZ5carkID7MfRTWmmyK765NbjYZPVN3ZwfCZSaKy8PwPf0cgq/vQ9t776PnI+14SsQY+MJvvKXSqPboZ2ijMPM6wx56jhvCEqfx8zL4l6pnb9R+rgQtTPnJW+VBcygkI2u7XZzAvB6hvqYW4wbNoy8vLZJ/Nar3MGrQGgLuNTCk1ZK/vKDUCE0vLcDW1ozMai+s4Qb4O1oQ0GlVzQ0otVtQYjXDE25CoLNV010iZq+vRnZRAfLLTfC2NCGo18/OFpib65EedMPZGsLiijGFfKh/AE6bAx0Gru0Z6O9XlTuvgzNkynJ9HcODg2oqRtas7T7xNGhDXS36eM2aQeonMLBUVOjP16srmK+jfPfZ56j76xtwffgxWvNyMOWwYc7twKzbnrRNUp3TXJAH5/HjqD1EAPj2uxgvLMTqaPL1L7cNLc3NsFksCiyM0ArVNa3hMDwul1rDda3W0dznxbGy53HJfhjDk53R69pa6mzH4OnTaHn9Tbjpee1nzqC3vFQzfhKxuSoHJmyVaE5NQfDwEYT37cdYVjZWhwejfzk5TUyMK7DiWaHJ8YnoVX3izXbhppBMg+4FbcDartoNGqcmF+ZgbSVYq/HB1t6MQG8ngr1duszTHkapy44SqoC97S0I9nVrukvEHKEGZJUUIY8aDC+BWg35WU3X9ZilrYlgrQqO1ibME1zrFU8nym5Q0Z3Wdt0Nuk4dQz5sW53heOAQaj//AtYLFxCmDths0BvZdZ6k8b3TAQ9CFSY4MtIRunRJjbZ1vfMuRnNzsTQ4wCGIBCQBXdkNajarkXMjlgzcajfo7OIkSmvO4mjRE3CGstXxHVpaJ+Cba25C/8mT6p3N3SdOwJOSCmt6Ovr4TTO12vEUr/Hu+UlfFRqKixC4cB5tPNJGMDiSlYmlXoLWJDdkyW7QW0tgLYYE1qKw1hZCoKeD4IiBLXm7EdYYuLTdxmuOUP1VWOtoRbUBfloI0oyGNYYfgTXRndR2hLX1hXkCMj96v/gCXW+/jeGUiwgX5sGakYHmMhNmCLR41/bmI3cSNT7SJ1RWCmdONjrKyzBemI++Tz9F5+EjGMnJIWAb5IeJhig+beWhuOv0X+dwA06ZX8d56wH0j7VGf7lWDGqzjfXoPfYVOt58S70KcMxaCX8+xSfD2sYh5jqM02LC60ZDaWRX/2BhAfq/PKbAcCg1Rb26b3018byVDKxxW8e7XW8mgbU9JIG1PQprMrImsLYLFQvWFqjhq6RytP+tfXiL7N1330Fubg7GqCHVkl5YW6c6ZoZAre/zz9UZjiOXLmLW7UB7ZcXtgbXsLHQSvMz63JgqLkDf0aPo5hG2vDws8whbAuHfynPWFpdmYW/MxJclT8NB/y6v3LjUZX1lBbOhRvR+dRzt+w5g8NRJ9c5mPs/ydsBaPdW5tSXFGK1yYLqsRE1fcxoOXU7FYjfFR4JHCcULawxnvHniww/exzNPP40XX3gBWVmZajfu9RJY20MSWBNYE1gT7RbFgrXBwUG89tpr+N53v4PDhw7hlZdfxi9/cTe+/OJzzbWwemBtnfzjEbU+8lu9Z/j8Ocw6bZgnGGi7AmulhsNah6UCc0G6TtcmGdg+PYpOnsYjoFlKoD7eSljjV0tdtB3GWfM+9AyHolc3idJynurqvuMMavvVWrWNVwEqWMvLvz2wVlyEsSonFiiNpkqL0c/QffgIhjPSsdTH6/jij5N4YG2G4OvixYt48E8PYN++N3GGnvPFF57HL+7+GdLT0m4AMoG1PSSBNYE1gTXRblEsWGsJh/HcM0/j8MGD6vBu3mxy6OABPESNY0PDje8VThbW1peX1Bo1nvpUozHnz2KG6gReXxaBtfLbDmvqb9H1iYI89Hz0cQTY8gjY4hxh2ypY41dJuZsLcLToSZTVnlejbNdoZQXzLWH0nzqFjrcI1E6ewjRDGa8vo7p7ksDqdsOaisuAF1MmAjZO0yNvqzVsi329FJfx1SGxYI3jt6SkBL/5za9x7Msv1ZmQLK5XX3z+OTzy8J/VO7A3S2BtD0lgTdasyZo10W5RLFjjo2AefeRhfEkNLmuF6pVTJ07g4YceRDAQUNc2i/NgorC2Nj+HmeoA+r46hs7D72D44kXMOiPvGd5SWIv+NudzEbDlqynRrrffwUh2DpYGYr/l4LavWYtOPQ+MtyHV8S6+Nr2Ilr5r02CNobehXo2o8caMoTOnMbsBZAxr9O+WwBr/poDNQ8BWggGCqS6C3+H0NCx0dai1dLEUC9ZGx0Zx6NAhPPrww+rNFhviNvr4V1/hN/feA5/XE70akcDaHpLAmoysyciaaLcoFqw5KS/xKNrllFT1fWJiQq1fe/65Z9UxMdcrUVhbm58n+PISGH2GrkOHMZJySR3LsVDtvwICWwVrV35nyFBTooVq00HXEQI2XsPGR1Hc4nlu+8gawcny6iL8bSX4suQZ5Pm+xPTc1TZoncq7WqN27Bja3tiHwdOnItBLz7PxbFsKa2z8tyl9pymu+3iE7SABJKXxIgFbrBG2WLAWoM7Cww89hGOff34NeC0RsJ47ewa/uueXcNrt0asRCaztIQmsCawJrIl2i2LBmqm0FL/51b048c1xBPx+fPbZUTz44APIysykvHGj+0RgjXd9zhCU9fIatQMHMXz+HOaoLrgeLrYc1tiojpv3uTFZVIC+zwgk33lPrWFbHiRAvckz3U5Y43PW+AzOkakeZHuO4quy51HbacHqWgQ41qmc8tRn3zffoP2tyGaCGZtZPccdhTU2hl8eYSstorj8nKD8CEY21rDdoj6JBWumkhL8lvJmdlZW9EpE3PadPHkCv/n1r+GtqopejUhgbQ9JYE1gTWBNtFt0K1jjF6anXb6Mb/3TP+Lb//PfeOCPf8BLL76AosJC1egpXQck8cLaOpWh2Zog+j6Pjrac4zVqG9N1Vxv6OwZrUVNr2Iry0fPJJ2rd1WheLpaHtA97vb2w5sbQUB/qu21q+jPD/RFGp/sijiid5lua0XfiJDp416faTBCZRt4cl2x3BNaipkYrTUXo//ILdabdSGYGFvkctpuMsN0K1jhu83Nz8et77lH5cbPm5+fx0Ycf4v7f/x4N9fXRqxEJrO0hCazJmjVZsybaLboVrE1PT+PLzz/HH+//vdpZ5/f5VB6gjBZxoAEjnAdjwdr6IoFabTX61FlchzF08TxmomvUrrc7DWtqVMjnxnhBHnoJ2BRkECQs8hq2657tdsAav90mrKZBXWjrakCB/ys1BepvLcHq+irWqT2aCzUSqJ1Ax/6DGDx1Sh3PEQn7dc9CdidhTY1W8ggbH+vBa9gOv612iS52U97TqKtuObJGcVuQl4df3v1z5ObkRC9GxJsKnn7qKbzy0ks3tKcCa3tIAmsysiYja6LdolvB2tDgIA7ufwtvvv46lqiOukY3AZFYsLY2N0uw5SNQizTWIykXMeuyaYIF2x2HtagxsE3wlCgfRcGbDnL54Fx+08FV3S5Yawk1U5m2wV1XguPlL+OS4x0MTXbx0CdmGurR++VXBGoHMHjmNGY2QO0mdkdhjW1jStRUQnngC7UecCg1FQsdlFeortmsWNOgNqtFTYN+dexY9EpEly5dJIi7W3Uwrq+vBNb2kATWBNYE1kS7RbeCtfb2Njz79FM4fOgg5aX4DjS9Fayt8SukCNR6j36q1qiNXDiPOfe1a9Sut+0CawoyeBpPncP2qdrZOMpr2NT7LyPPeLtgrbW5GRZzKTKtX+DzkmfgbM7F0uIcFltbI+eovbEPAydORM5Ru0Vcst1xWGPjMEaBrV9Ngx/GUNplLPZ20xNfjbNYsNZN7fArL76Ae++5B7m5uairq0NKyiX88Q/3Y9+bb2BwIArTnA7RtBBY20MSWBNYE1gT7RbdCta66NpHH36AjPQ0+i0+8LgZrKk1arV8jtqX6Nx/AEPnzkSm624yorZh2wbWohYZYcsn4Dwa2XTA57CpYz3WVZ17O2CtuakJmQXn8WX+y7hoP4KewQbMh8MYOH1GrffjXZ+8mYDjaWMX7c1sW8DahgWq1KYDBjYVl9nZWOrrvTLCFgvWuG6qcrnw+KOPqpG0X/7iF/iHv/87PP7YY+hob4844jTYlA4Ca3tIAmuyZk3WrIl2i24Fa/waH07zCWo0Nzd4t9INsMbXlnkzQTX6PidQO3QYw7xG7RbrqjbbdoM1tnk/AVshAdvHn6Lj8DvqXaI8wsbx1RxqNhTW+Fy7xlANvs54G+/nPA5b/WVM1AcwcCJy4K06R83J08i3hrQN21awRsajlWqE7dhX0XPYImvYqPLC+Pj4LWFNieu8nh51xExGRjoe/vNDamOB1+OJ5Ge2TekgsLaHJLAmsCYja6LdolvB2jWKEzyuhTXK1/NzmK0ORs/YIlBT7/q0azbcWrYdYU0tlOdjPfjl72qE7V2M5uZiurMDoaZGWM0WQ0fWgiEHPsl+AV8XvoiQNQODvOvzwCEMnjwZOfC2lkBth8KaCneQ33RQQnkkuukg7bJawzY2NAhPVQxYu07VlNeefOJxArb7UGYqxcp1QCawtocksCbToAJrot2iW8IawwYbX2eLAz6uwBqVvZb6Wsz4vep1Q10Hj2D44gXMUlmPFyzYtiWsbZivCpMlkU0H3e+8h760dNRZzJGRtS5jYG1mfhKWugx8lPsX5KS/htajH6LrwOHIZoIN0IoxOrnZth2ssVF+UCNs/C5R3nTw9ttq00F/0K8OA3Y73bFhbSOu6d/ujg4U5uejob7uhjQQWNtD2oC1+pqaK6//0Ct+514d+Wcur8DI8HD0qj6trCyjNdxCEFijzp0xQlOLC7C2RWDNTv8yxDAI6TEvwZqJKvBSgjUfg1V/t6a7RMzR3ECwVoy8ygr4utpQY4Cf1vYQMoIeOFtDWDCokDMEOW0OtEeni4wQA5WbKrj2NgbA+BaF30rr62sYGhig/Cmwthu1AWu9BBdGiTsMlpISNBAI8chT9/6DGD13HvOuyLs+l9iokY7Hlsm44W8nWLMRXIQJsOYI1vi6lvt4bZbggMHPRWHsJFhjaNByd3OLPIdaKF9UgP5Pj6Lt4GH4j34OR04uxScvltevgfF2pDnex2fn7oPtg+fR+dYBDJ88pUbUVDwmEJdsyxTuaQKrQBTW+u1WTXeJGKfFlM+NBqpz6wjWxj3OxNOHnmOR4nLaVIRBgvvuI2+j9cRJgukcVDlcmBifiMaIPs3NziLcFBJY2wviBO5qb4fb4VAH7vX29FJPsid56+lR7zXj3lg+FXKuOPt6+7TdxmsUpo72Dmq0XdTDNaO1pQV9esNJFqJwFlJhv+h3oaChGmXN9SjXY+F6lJI/WQ4LsqgyLvN5YKbelJl6uXqsmMDvYmYmLuflooJ6vxYKs5a7RKyQ/LnotqEk6EVbR7vu+GTg5/cuFhcUweOqUtMmnBe03MZjHB7lZyCA0qJidYhmZ0en7vzJ4WLg54W83AivGTBaINo+mpqcgt/rRdDnQ4/Kg3ryC+XB7m7UBgMwpV2G48vPEXz/PdSdPoHW8hJ0uK1ktoSsM/pvoKwYpswMeEoK0eayXLmerLU6zfCUFqI8NxNBFTZtdzGtyoZ2WwVCWekIHv0Ujvfeg+3CedT7/RQXWnEUv3V0tsFSk43Pcp/E8eN/hu2j/ag/cRwtBDTtBL78tzXDdAvjeAvbzbAW5KA0KwN1ZpOmu0RM+emohLukAK6ifDRTfCSTPuoehxnNeZmoobxT9fGHKD/5DczFxWhqaFR5k+P01tat6kEe3VWflV39nSHNV+VRwLayrH/m4U5KYC2GGNbaCH6K8wuQS9RvKi7RbcUFhbh86RLOnjqD3KxslJWUarpLxBgCMi6nI/ViigqrlptErYB6yxfMZThJleUFnxOpBG167ZLPgdP2CpyiivNibg5Sqaer1y5cvoxvqPd54sxZXKIKPjVH210idiE/FyfLi3GJKvZiqjzKNOInEWOgysnIwnkKY2Zauvqu5S4RU35mUljPnldpX1JojJ/52bkopc/dVPEZMbUj2j6anJyEzWJV+caIPGgqKkE+lePLmZeRlp2KrNw0ZBfnIKeiSJdlmPKRWpyL9NI8ZGv8nrCVFyLdlIfUklzlt6abRMxUgKyCTGTkXEYG/VtQXKDKjGYcxWk5BZdxNPNV7E97GMeyPkBmbgpyDIjLbHr2tNJcFZ+ZZQWabhK17IpIfKr0KdfnZzaFKbswS8VlWtZlZGZnopDaMI7PuI3ycmlhUcT4c9QK8wpQVFCAUGMjVlYE1na1GNY629tht9ioR+pTU41M68ka399Y34DyUhOyMzLh83gVDGq5jdfYT+6JWC0WlJG/DXX1usPJVt3YgHy/B1nVXrg7WlDf163bXB1hZNV4cclpQT71Fk1up27LN1fgQloaUrKy1Fo4U5VL013cVuVEHvX6LlBvvICH+5sa0RbWjqN4rJXuDYea1U6n/Jw8OCgv8ZZ/vq7lPh7j9A03N6PK5UZBXr7Kn7zlX5+fYTSHQipPOm129Pb2yMjaLhPDGr8/kdcG8Un5uvMg5WuHj8qz2YSLjkrkV1lRpNfcVmRbSnGZ4CK7khpcl1nbXQJWSB3OrMoSXC4hULOaUEh/Q8tdIlZAluasxCV67sqgB01c/jTiKZap+rupHkX2VBzJeAz7c/6KE9Zs5FIdpPV3E7UCqscyTIUUn3nItZUb8+z03FkEWplk+fRZy00iVuixIpPS+aKtjPy2oqauNom82XyD1dXUwu1wqvpWRtZ2uTbWrPHU0MjwiBpp4IW5SRvdPz83h5pgEJWmcrU+yAg/edMCV5zVgSBmZ2b1+7m2jrG5WdjamlEZbvj/2nvz9zaONM/z79r5eXvnt52dnena6e6pmZ7p2dl5uqqPqi6Xy66yXb6vliyr7PIl25Kpg+J93wCI+wZIgCQI3iB4n+B9St993wBAgWRSODJFUdD70fM+VCYjg4HIzMhPRkYkML+xjkO6Mzk8Li2OKA6ODjG3sQbz6CAaSdgcozE1aUFvOGJR1He0odlsSk9amJnSTFdMWMeG1AQDx+gQdvZ39dUnbcsD9/mxIksVN858l6c3T35xKT9KdTkdGBvlMRkHuvPkcvFEiAgdnzJmrfxQY9b6+9Wg7Ed0ThpxDI7MJlHtdaAu5IE7PoDAWAx+On/0hMnrRF1rE7rpwu2jPP168hwfgnd4gPKyo7GzHZaAG346rzXTFhEeahfb+3yoofz6qM3YO9ineimhPul+KLW9jM7wbXzS/Evc7PkKDwMO2ONRqkvtv11o8PaeWAStpi7UtzbDFvbr/+xUn+6hfnTaLeiwWeAa7ENgXOc+pzKZBkKo8jthGYxghY5TXcdmJjYpn+HBIRI3GbNW9mRljWeDrhY4nTgf2QkGPBvUqAkGXE6WACMnGKT2duGYiMM6MoTlrc3MDJzSgwevL22n0KtkLQAniaDW4P5iIz3BIDMbdMqYCQbW8eGT2aB7JEFGMD83p2aDqgkGqi71oyYYOJ3GTTCgBk5NMJDZoGXJqQkGBhyDnMPY/CzJmhMNdE77eIIPn0M8GamUoG35ZssS8qOuvRU9PJNxeiJ9Xp5NW2jMTiFI7UKP34uGni5Y+0MIk1xppi0iuFwdJCq1JKn9Mwl1U1oK3C5OLkVRYX8bX/e8hUp/O2qoLl2TI5p/t6igeuNJXa29ZtS2tcI+ENFOV0xQnjyrv9PtVOOFvaOZdlwrbYGh9jnJL4tv71AUa1tbmdrRB08wkNmgLwm5svayvbpjfXdHyVovy9om3+nQ3UqJQRagZGJxa/2JrI0Nq5NUb8hLceXVHUJhFPyetQLhx+SjczOnZE3X+ZfZ9pSsUZ7n0hUTJGuBE1nrPpE1zbRFRGB6/ImsJafUk4NS2Npdg3WwCt+ZXkVb+AE6h4Ika344qe3V+rtFRUas0rLWRrLWT+t1fvZMnllZ84xSO66zzeWnGbmytrq5makdfcirO14iRNZeUlmT96yJrJUhImtGyhr3rPWTrHlLlrXjR0eYWIzinuMD3Ld/gIFkmNrHGKr7fFdf1jwkay6RtctCZC0PImsiayJrQrkgsna1ZG17dw32oVp83f0bWAYqMbc+j15qF0XWRNbOIrKWB5E1kbVylTXeL8ePT49zE1krb0TWjJa10h+D8vmXXI6h0vkxfjD/nuoxiLXtrUzPGrU9V13W5DHopSKylgeRNRmzVm5j1nh/JFJxtI7cQePwLcSWAjg4Tn9GkbXyRmTt6oxZ29nfgnekFd90/QZtwVvY2F7Gxt4uLKNDImsia+cQWcuDyJr0rJWTrNFewMhKCF/5Xsfnrl/jz97XcN35T+ibt6nfPz5+JLJWxoisXY2eNa63ubUJ1Hk/xy3TaxhIONT4NZ6B/0LJmjwGvTRE1vIgsiayVk6PQdd2F3E7/AG+8f0By9szGF4K4iPr/4f2kQr67WOStccia2WMyNrVGLN2cLiLvkkLvjP9Do2+L0hOZtX69d3tF0fWZMzapSKylgeRNZG1cpE13g8Dix58bP9fqI7cRHTRjTvhD/Gp7e8xuOBOp5GetbJGZO1q9Kytbc6rR5+3el5DaLwHR8fpdzm+ULImj0EvFZG1PIisyZi1cnkMevToEPapJvy249/hNx3/Jz60/r/4MfguBuZdJxcLGbNW3oisPf8xa8fHh4jP+nDb8gbqvDexnEpmfiOyJrJ2MSJreRBZE1krN1l7z/Lf0Rq/g5mNMSxvzyK1t4zDRyJrLwMia8+/Zy21vYSeyF181/MqAmOddN4++YaUF07W5DHopSGylgeRNXkMWm6PQT+y/k9UR78gWRuHeaIGNQNfYH5rSqURWStvRNae75g1nkQwNhdGhfVdVDo/wdzaeOY3aWTMmsjaRYis5UFkTWStnCYYbO6voW7gS7xt+jk+dfy9mgnKwrZ/lP4+WZG18kZk7Vn0rBUua5u7q7AOVuOb7t/CNlSDvcPTbfULJ2vyGPTSEFnLg8iaPAYtl8egWbb31zG4QJ9tqgXx5eCJqDEia+WNyNrzG7PGY9UmFvrxwPERKmzvYXIhqs7hXGTMmsjaRYis5UFkTXrWyk3WnobIWnkjsvb8xqxt7q6p3rRvul+BKXIX27upzG+eIGPWRNYuQmQtD1lZG+iLYHVlLbNWHwf7B0r+envMWF5azqzVx+HhEcZGRhEJ92N3dy+zVh8pkkonnZRWkrWVLT55+C5QR5CwLW2nYM3Immssrhp2veEaHjyRtcDkOPrnpjXTFRO28WElay4Syj2DTvKFuXm4bE5MjI2TaGVW6mRudg4epwsT4wYJ4KPHWJyfV8enyFr5IbL2LMas5Zc1vmFNqK+W+gQ/mv+A+IwvfRN7BpE1kbWLEFnLQ1rWEiRBYSwuzuP40aF6zUGpwdtvb2+iLxyEqbsb8/N8QTzSTFtocJ67dJIPx4YQCgWwuZnSX87jQxK0FGxjMZjiA5hLrWL/8KDkOKDYO9zHTGoF5ngU9X1+2Ojk9E+P6w7bEDWYnW1oNPfAQw1cIDmhma7goIuDmYSyOuyBncq4ubulsz4PcXhEnz2ZgN1qxcjIMA4O9lQda6fPH1weznN6egpOh53yjGH/YEdXObk8hwe7mJ2ZRn84hFmRtbIjK2sz1KYZxTi1YTW+HFmb0XPhTm9rzsiaiWVtehJ9em7A5hIkfBOUlxeNJpK1SJjKOKWdtogIkGB0ctsT8iJC5T48Pv09u7kcHO2qmZ/f9ryK1tC3SG1rP1FJ7e2kZa3fB9fkiObfLSqo3vyToyRrFqrPNjgGo9rpiolMnl0eJzqzsqZrnz+RtWqWtdgA1kiyjGBnexsjsWGRtZcB3sETk3GYnA2wBGvgH2mHb6St5ODtXYNNqLd8j4rmmzAHqxAY7dBMW2hwnu6hZrQ47qDOfAuOgUbd5fTR9rZYJzVEZpIWL6yjMfimxqgx1hf8CJQl6K7PhpoQN/Au3VHtt+K2qRkVljbUhR1ojLg10xUTVWEnbnvobjTQBudwK9Vnq0YdFRHxVnT7K/Gg/Uu0uirgoWXNdAWGn8JLeXT5HqCy4yu0cZ7DLbr3u4c+q9lfA4uzBdPUiJ4dUyO82GykUggHgkrYFhcXsby8jKWlpZKCt+U8QvEYHriteBh0qxs7biv4y8gtmZ/Z4OXcdRcts6y0+N2o7GxHq9MOa7QP9sF+1StUanBvWrPFhKrmZjXOyh7VTldM9EbDaAp4UOl1wDVMN7QLc+pJybl6ohibHkSt8ya+aP0X9IbqMTeXpPpbOZd2YiaJjkgI90l+e+inQ+PvFhVUb5ZwUIlaZX09CZZLO10xwXlSfTY5rKh3WtHNy5l9l7svs//P3bcXLZtpnzcPpD93RzhA9ZXQrMtiIzFFEhkMYWQ4jqND/cNEnicia3lgWRuZiKCy6ya+bP4Nvu36re74uuM3uN7wj/i46u/Vyftd96ua6YqJbzpfwedN/4Tr9f+Ar9oNKCeXyfQhvrE/xG2fVXXLN0QCuoPF77bPju9cZnzv7sEP7m7dccvZia97W/GNtQ0/uLTTFBu33CZ8bW/H1+avqT5ep3jldP2UEF+0/Aqf1vyC9tM/a/6+lPhTM+f5S5UnHwNaaYqJrymPr1peQ3XPd5hKjomslRksa/zY3NTVBY/LBa/bDa/HU1L4aFuPx40Ouw23rSbc9troJseL2j6/iprMz9zl3HUXLdf0+fDA58CP1h7cN3ejrqcLDd36oo7E735tLe7cu4+HjQ1ooM+vla6YqKe4392JO73daHba4Ka68Ko4XU8uksP6nju40fBrfNfyDsw2ujGiuvO5T6fjsLnp5pMk6DZ99hoDPjdHXXs7Kior8eNPd1HV1ETl7tRMV0zUmLrwE5XxJ5L0qpBHc19m/5+7by9e9uF+wIkfXb2osltgdTrhc1Fduqheioon23jo/w6rDZYeM4ZjMRwVMFv3KiOylocj7lmbiqPTXoMO7126q6jVHZa+h6jq+Qq3m66hzVsBx1CdZrrCow69kWrUWb/Dw+4/wxR+qJGmuLAN1KK9rwEP/NQoRfyqV2xoPomhhdJjkMI7Naak7a7fQSepG01Rn+6oDdjxk7kd96zUCPV70Bz1a6YrNBojXlSGXLhNMlnvbYQ1UgsH1bGe4Ppsc99BRctnaLDdouUazXQFR+aYaXXfRkXb56i3fk/lrKY7X9p/OsIapePccw89jsZ0z9ojkbVygh+DBv1+9IWCmJmextzMDGaTyZKCt03ST+/gAO65bHQ+px/dBacnEEiM6wp+JFYZdKOae5jCAfT2BXWFKUDndU+3ErVWm0X1NmmlKyZMVK56rxMPPHY6F/sxlUhQvTypz7nM/wdiQdw3XcOf21+BI9KiJgXNzcyepMuN+MQ4Winfe14HOoM+zb9bbPBYvZqWFjyorUO7w07XH+10hQZv3xb04j4JdUM0AOd4XI0r1NqPhQYPPemJR1EZcKEt5MPw2BjmpqlOio7pk//z8T0Wp+PR51c9a/IYtMxRY9amEuink3tufgYHR3vqS3hLDtp+c3MdIToRe7o7MDObwKEBeW5tb2BoKIpgwI/11Krucu4d7GBiZQ7tsT71aGNhYx2HPKapxOBxWwdHB5jbWFMNcUO/H7bRIe0xY0VGesxaO5rMJnio4dA7Zo3FtCPWj4dBJ/yjg9ja2dBXn7QtjydLJCZg67VgeHgQe/vbhuQ5RY2c3dGr8tzd29ROW0Ts7W0hOT2ZPt5lzFrZYfgEA5L5+NxMemD4yBDWd7bo2DzUHLdaSPDYVv45tbqI1sGwejTmpWNca5xTwaEmGIw9gwkG/OqOp78Ul8eCxpJe3Lb8EXWeG1hcf/pYQTXBgOqxisSXJxjw2Dqtv11w0GfnyQAtuRMMdH72EEXv2DDqqA13UHu7vJk6tx+LCd7n2wd7GF2ao30eQi9db1bVhDaCe/Z1xPbmpkwweFlQspaZDbpm0GzQQ54N2h9Rs0FXDJoNys/jx0bGEKFy7hk0GzSZWkfXcBRmkqsVNTuHTgAdwbOflkgqedxaUyQA17gBA2gpjJ4Nyg0S3+VVh9wIT47i6MiYsQ5PZoNOpKvEAJ7MBh035OILNRt0gY53mQ1ajuTKmrqg6YRziM/NoibohoMu4Dsnr7l5ct6XEnMbq2gf6iNZC8M79YK8ukPj1TkbO0swRe6p13V4RlroxvXprwF6EWaD5sqah/LeoDJr7cNi4ujRMQn6Eu3zMEk/ydqOQbNBt7dF1l4WsrL2sr1njafkT6+vonM4omTNuPespU5kjbvPtRqDYsPo96zxzKTujKyFqDHiOz+9yHvWhKvAs3h1R1bW7GMxbO/zjWL6xqyU4HaCf86mVl4AWXv6S3G5V210Loh79vdw3/EBkivDmd9czIsma27KO7WzdW4/FhO8zw+p7ZpcWUT7YEbWtuXVHWcRWcuDyJrImsiaUC48W1kbfslk7WkvxX1MErOE3sGH+M70O1gHq7Czf/4luGd56WUt27MmsnYOkbU8iKyJrBkla/Mia8JzRmTNaFnTHrPGY3QnFqKodHyMCus7GJ/vo4928XvYsoisiaxdhMhaHkTWRNakZ00oF0TWLqdnbXtvHa7hRnzX8yq6+m5jc6ewsckiayJrFyGylgeRNZE1kTWhXHiWsuaQMWuqTtR5uTqKas91/GD+A2LTblqXv1eNkTFrJGs8G1Rk7Rwia3kQWRNZE1kTyoVnK2sv62PQ07LGr8AJTZhwy/Q6WgLfYn1rQa0vBOlZk561ixBZy4PImsiajFkTygV5DPosx6zR+Uf1sbw5g5bQt/jR/AaiUzb1fb2FIrImsnYRImt5EFkTWZOeNaFcEFl7lmPWjtQLzgeTTvxkfRtN/j9jhcStGETWRNYuQmQtDyJrImsia0K58Gxl7eUdsxah5f2jQyVnHeEf8YPlDwhP9BTVq8bImDWRtYsQWcuDyJrImsiaUC7IBINn07MWmUlga28LQ0k3frS8iRr3dSyuT6YrqQhE1kTWLkJkLQ8iayJrMmZNKBfkMaixstZ5MmZtEgvrSZgid/FN92+pTWrA3iF/DVNxyGNQkbWLEFnLg8iayJrImlAuiKw9G1kLJkYwlPTigeND3LW9i4mFCH0O/t7L4hBZE1m7CJG1PIisiazJY1ChXJAxa8aOWetUj0Hps48EYYpU4gfz72GOPsDGzmq6gopEHoOSrMl71jQRWcuDyJrImsiaUC7ImDXjZa0q4ERTuAMVto9wz/E+xubCqq0rBZE1kbWLEFnLQ66sra6Udrd0loP9fUT607K2vLSUWasPLufYyCgiJGu7u7uZtaXDHfjJ1NqJrK1s8snDa0sPPjGXtjeeyBo3RixWOsMZH3wia9Qo981Na6YrNLgxypW1w5yvkdHDPEkQy9rE2DjVBdeJflioWNYmxlkAS7tA5MIX8MX5eZG1MiUrazOJBO1s/ccg5xCfnzvpWdvJyBpfgPXE3BlZ66NzsuSYOy9rfSRrmmmLiOD0BLqGIrjnMeEH23f4qvtV9EQqsLW7puqmFFJ7O+dkTetvFxzUFp6VtT6SNc20BQaXKVfWNkjWtPZhMXFEN4lTOY9B1zhPA9jZ3hZZe1nIylqEZG1pcUldZPkCVmrw9ru7O+gPh2Hp7sHCwoIhee6TAI4MD6MvFMYW3U3oyZMv2HzyJNZW0BGLwEQytLiRwjGtOyYhKCVYJI7o7ml+c50aI5K1/oB64zn3YukNZyyK+g6SNZMJ/onR9N2fRrpCQzXCw1FU0QUoOB7H/sG+qk+ul2z9XBSav+d9QXU3NzMDh82upPro6Ogkz7NxNo+n5TmTTMJFsjY2OoKjw4MLy8nL+fN9jOND2kckaRE6PkXWyg8la/39mJ6cxHHmGMweG8UGb8ttwvDsDKoDbtjofN7e26X1/Pv0OV9s8Jed88+Z9RW0DfahKRqCZ3JM8zwtJrjHvdvnQUN3N3r7QgjROa6VrpjwJ9I9a9/b63Gt/S38YH4DQwkXnduHJdUrn4Nr25vq5riKZM0xbkz76KU2rIVkraatVclaKKnvswcpLKOxE1lbJ7E6ux+LCd7n/O0PEysLqmfNEh/AinqSc759zNbTRctnY5OO9+GhIZG1lwHewVMTE3DZHegLhlSvCD/GKjV4+2EyfTOJWlNtA0KBICbHJzTTFhqcZzw2DCeJgInyHRoYxMS4vnKOjY7CPxhFbdCD+kgAProzjc3NIDZfegzR9t6pMTSSqFW6bWj1ONFDDajeaLVacK+6Bg8bGtDFedIdtFa6QqPb50a924G7zl6VVzweT+8j3vcUXN/ZyLesIrN/gz4/2ppb4HKQXI2MqH2ktU1By5n96/f60NbSqvLkBmkyJ8/c7c4uZ9edXWaRDAUCqrduhuSSG0OhfNhIpRCkY8bv9qhjUB0XOed9McHHDLcTDpKfe24rWklc4guzmFpdUo+09EQwMYGasA+VARfaIkF0RcO6op3anFpHL+53daCR2gitNMVGRySMKp8NN7q/wbt1/4DbHR8g1O/KnEvadfa0mKCIxobQFPSiwudAM5VZ6+8WG+1hPx6aunC3vRVN1LZ1kgBrpSs0Oika+ny4T/umc6gfg3NJzX1YTIwvz6trQ23Yi5aABxGqh2yblG2fil6m+uRrodflVh0ZR3Qj+iIjspYHljXe6Z2tbWhralGSpTe6O7pQXVmFitsVaG1sVo9DtdIVEz2UZ31Nncq3q70Dlm59ebL0tZh6UGEz4UePDQ+CblSHvKjRGZWUzx2HBXe62/GgtRlVTY2oatYX92tqcOvHO/jhpwo8bKxHVUuTZrpC42FzEyo62+hOuQs1XZ3o7upWvaBa9VRwdFF9Njbhwd17aKitg4ny1ExXZKTzvE951qPHgDw5DxbKnq4uJKen1d2tUD6kSNb4pq65odGQY5DbiSY6Vu5YunCPBKMxGkQLyYCeaKaooYv2bRLAn6jtqaR8q3xOXfHQSzdfdjNuUznvk7RppSkuXFQuO27ZG/Bhy9v4uPYf8aDla/R0d1G9lN72dtG1oLrXhNtOC+577Rp/t/h46LHjjrVHtWf36Sa5yoD6vE958P6573eigaSS95nWviw0svv8J7pBfkBi2dFtTPvI10IO7l3jpxkvMiJreVA9a5OT8JCdxwZjmJubw9ysjqDtE5NTsFttaGlqJvMfUGOZNNMWGrT99FQCPo8Xtl6b6snRW86Z2Vn0j42gPuhRJ2bbYBg98QF064yOgT7UOayo7zXDHPKjtz+kOzrdTlTWk6g2N8Mc9MNKd7xa6QoNS1+I7m7pc1PDZu0LIpFIaNZRMTE7M4tofz86qeEI+PyYSc7o3kecZ4Ty7OroRMDrU3Kle78nkxiMROFze9TkBZG18iKV2lA9p32hEGb5GNQ4BooJPgb7olE0kWB00PnsnhyhGIVHR/D2Xf1B1Nl7YY6G1WSA/rlp9M8mSoxphKcnYekPo8Vlh2Mwiv4ZrXTFRBL+xDBq/FW43vYKHtpvYGQiQm35vGY9FRqJxDQ81P60Uzk9o8OI6Prc6QhOjaHD50Yj1acrPqSZptjwU56dYT9aAx7YRobgoWWtfVlo8D63xOg4ctrQ5bQjPjqiWT/FBvdwcnub7lmTx6BlTXbM2kB/BOtr65m1+uCDhgf59prMWF0xZoYpjx3hrvQolZPHrxnB7GZKvaG7jsTFZdDMTR7s2uVyoJMiODWO/oUZ9M9Tg6Qj3NRYNHR1oMViUY9PIgtJzXSFRt9cAj2jA3Sn50EfNUI85s4IlhYW4Ha41CNVo1iYn4fX7cbk5DgtGSNWy4uLalyTjFkrP3jM2iDJ1RyJvVHwWMxeOveGR+LYOdjHLrVvu4cHJcWe2nYf4xMTsNvtGB0bxR7leUTH4RGdh6XG7t4eRkZIDOgmJEk3JPw9nlrpCo1Dam/n1xJo9n+LP3e8Am+8jdoJ/bPGHx0fqcfTHpcLS8tLOObB9xp/v5jY2t5GKBiEzWrF/MK8mnmpla6Y2NzewmBsCJGBKFbW17B3VPo+T8c+5qjdcdP+8Xq82FhPZWpEH3u7uxgdjsuYtZeBrKy9jK/uSK6von0grGTNqNdsKFlzk6zR3ZOaDEB3aVrpigl5dYe8ukMoDKNf3cHH4AyJX6/JpMYJGcUMtbkukrXJMbpZomNSL3yDzMNZuMd4fmY2s7Z0jo4OMJz04gfTm/i24w3EpkKqzdTLAYnp6PAwvCRrawbdyPPNe38wBEevFSuLxrx9YI/lNxbD8OCgmnFpBOtra/CTqHmcbvrsxrx5QV7d8RIhsiayJrImlAvPUtZ4cDcv64XzSCYScJKsTZCsGTHW6JDaRz7vWNbmSNb0lfMxUtuLMEXu4dO6X+BO22eYnB7j1brJlTWjnrqwWPHkOJa15cwbDfTCr4eKk6zFSNZYiIxgbXVVDeURWdNGZC0PImsiayJrQrkgsqZf1o6ODzG+0IcK6/v4uPIfUdP6E6apvAZ8dJE1kbULEVnLg8iayJpRssbvLxNZE54nImv6ZW17bx2O4Xr8uf0VfFf/Ado7m0nWjJk5LbImsnYRImt5EFkTWRNZE8oFkTV9sqY+78oIaj038H33G2g134fVYsn0rIms6UFk7emIrOVBZE1kTR6DCuWCyJo+Wds72EZgvAs/WP6AFu938AcdsPfaRNYMQGTt6Yis5UFkTWRNZE0oF0TWSpc13mZhdRyN/i9xx/pH9I1ZERsaTMvalMiaXkTWno7IWh5E1kTW5DGoUC6IrJUua9yrFh7vwe3et9Aa+g5zK1MYicVhs/SKrBmAyNrTEVnLg8iayJrImlAuiKyVJmucfnE9gdbgt+oRaHjCjK3tDZE1kbVLQ2QtDyJrImvyGFQoF0TWSpO1/YMdRKasuNP7Fuo8n2N+fUK9bDYeGxZZE1m7FETW8iCyJrImsiaUCyJrxcvaY/q3tDGD9tD3+K7nd/COtGL/cJfa3EORNZG1S0NkLQ8iayJr8hhUKBdE1oqXtePjQwzPeFFhfQeVzo8xvRRT67nNFVkTWbssRNbyILImsiayJpQLImvFy9rm7iqsQ1W4ZXoNtqFq9VJc5mD/xZO1JZG1FxaRtTyIrImsiawJ5YLIWnGydvzoCInlQVS7r+G+40OML/TTOZH+Yvl9kTWRtUtEZC0PImsiazJmTSgXRNaKk7XtvRTc8UbctryB3oGHJ71qjMiayNplIrKWB5G1HFljCdIZp2SNxCo8N62ZrphwxnNkbWocfTrzDJGwdY8MSM+ayFrZIbJWuKw9fvwIM8tx1Lqv4779fYzP9/Ha9C+JF1HWZMzai4vIWh6ysjbQH6GTx5gDiE/IaH8/NXBmLC8tZdbqgxu0sZFRksB+OpH2Mmv1MZNaI1nrQ53fpYQoNDWqO7zxQXQ5rOi09cIXH6J1Y+fSFBvOaBiNba1oNXXDPxZDOKEvz+DkCLqH+lAVdCNMQnl4bMxJzhLksjvpAjTOV4LMWn2wUHmoYZ8YHzPk4svlWpyfV8enyFr5kZW1GZKhHO/QxWwyCavZRMfgRGaNflgAXXYHJsfHDTkGj48O1XnnJxmYn53LrH06+/zVUmMduGV+HV2RO9jaPd3+Hx4cYmQ4DjtJEF8jjODo6ABj8ThJJQkLyYsR8CtG+kNhOK02rCwtZ9bqY39/jz77MIaHhrCzrb9zgFlfW4Pf6yNR9WB9dS2zVh8729tKqEXWXgJ4B09NTMDlcCEajdJJmVR3UdN0cp7EueVMnF3HP6kRGqM7PP7y3+aGRrooUsM5PaOd/qI8TpbTfzc5nVQNEfew9JotGB0ZySlnTtl4Obes2eVsvupvJlTDk6Dt+uhkbCBRq3Sa0eazo8fvRLffoSs63DY0mjvQYOpAp8eumabY6HBYUNvejLquFnR5begJaKcrJNRnDDhR77XjnrMXvSG/ugil6zNbR8UFb5uYpPoMhdDe2gYv3d1PTU7l1Hnxkc0zRHfMHW0dKs9JOk6ndZSTyzM1Oal6Z90kgDN0EX78yKArunAl2EilEPT7EfL56fiZUm3HSVvAP7OR2y6cLOekod9xO8HrQoEAmhob6Rj0qnbjVJ5n8zjVHmXXPfl9tu0J+gNob2mF18PH9WQ6z2z6M9uk4+xybpppdQ57SIC6OjoRJnFJnPr92fT8/wSiIz5U2q7hZvOv0eWpxsTk+ElbzeXknjonCWVLUzP8XJ9qu9zPfibP3OXsupxl7k1U7bjDic72DgxGB9J1nBvZz3mynC9Put7QTbzFRG14c4t6QnTqs3NoLeeuy9Z7Zpn3xdjoCJwOBxw2O0lb9nqTTVt8JCgGo3Qj39FFn71T/V9vnhxxkmmf16uk+uhQfw/t80RkLQ8sa+Ojo+hoaUNzYxO66WRX0cnRlf6plvn/mThJk113ermjrQ1VDyrx0+07lGcjerLbnKTPLGutO/d3O9X2nXTBrq2uwcMHD5UQPMkzE9n81Lqc/HLXnVruRFcnSVVHMx621aO6ox41plbUWujv6Igaczsqe1ooWtX/tdIUG9WUz4OuZhXpPHXkS9tXdzbiYWstHrbUoam5SdUtNyJd7aUG1SX9bKxrxN2f7tJ+qj1Zpy86UV9bj7t37qKmqobK2a72XRc19KUGf9bmBvrMlA83zEY8MhGuDimSNbuVbpjqGmh/p8/zk/Yh2y7kthdn2wqN5ca6etWW1dXUZtZl4sJtMusuWqZooDzv/lSBOmrT+Lg8+/tzeWbXnV3OlKOzvV3ldf/uPTTVN+T8PmebnOX2tibcabiJT6p/iS/r3kBTWxV6qA04SU/58vlWU1WNijs/ob6mTong+c+Ws03ucqZc3dk8s+WkPGvpXH5A5Wxtakq347mhlce53+eso+UOuh5U0vXm7p0K1UHQ1ZGpTxXZPE5vcyrfk+XsunSe3OZUV1aTBLbR77Xap2KiEy2NzWr/3Ku4q/6vN0+WPi5be2s7YkNDODbgcfrzRGQtDyxr01NTCHi8qiuVH1suLy1ieTEntJYvSLNC288lZ9TdE985jsRiWFleLiqPs8ucJ3fthwJButNzqrspXncqfTa/p607s5ycnECgox22P92A77NriD6oQNzShTGXteQYspnhbG+Bo60ZMbsZY27tdMVEpLcb3Y21sDQ3YNhhwXiJeY7StgMN1Qjd/BzeG9dgrriDsM+L+bk5qhOqz2y9FRu0LY9NjA0MUUPXjXAwhIX5ee20hUYmT777NnV1q33Pj1lXsvuyxOBHoHFq2AJenxoPJ49Bywt+DBoOBtWwjqWFhXQ7wfv+7HGT0w5ctMzbqmMwElUXb+45Xlrg3+XkmSePs8sqT8qDy8dS0EdlTR/XmfZMY5tT684uU/A5weNFedwWDz2JDQyoz34uD067uITFxXkMjgZQab2Ob7peg2OgGfPzM6friv4/R+dHwOcjMehANEL1mc3vTJ6ayxrrOH8uZ9DnR29Pj+okOPmbudsUtbykHlM7rXYqZyf40eVy7mdXaXL+n13OXXdueUn1ugeonDzGjK+P5/IoMrjuxujzcg+gucek/n/usxcZnGeCysbt7ehwnK7lImtlTe6YtTWDnqPzYNeTMWt0QBlB7pg1HlBqBNtb2+i32+H68s8YfuddzHz0CdbrarAXcOMgEsJBf7Do2PC5MUh3dtH2NmwGvDjUSFNsLLnscNbVIUB3otsBH46KLRun7wtgs7sTs5/dQOKP7yJRUQFXcwuGh2KGCQtLn4skfWJ8PLNGP2rMmtOlBmLzgGjdZMasDciYtbLkyQSDRGaNfvjCzcMvjDyu02PW7MaNWTs+VnkFPB4lRE/j8NEBBqYduNP7Juq8NzC/rv25+OLPj9ccViuSVF4jOKLrzWhmzBqP4TICnnzGY9YcVhtJlUGT5Pb3lfjxmLVdAya0Man1dTVmjSeB8P+NgMs2ImPWXg6ysvbMZoPSXY4RGD0blNnc3FTjW9wdnZhqbEDy+mdIfvKvWG+ow27Qi30SnT2SnGJi3efCAMlahGQtFfBgXyNNsbFAsuYgWfOTrLEAsoBppdMMThsOYKOnCzOf38Tk2+9hpaEB6xPjqtGIDQ4ZMhuNHyey/PAYl3ESKyMuQJynmg1KAsh34TIbVMhHVtamJ42bDcqiwj0ifFwb8dhc5ZlIwGmzqZsQQ2aDUjvOeflJgrhH7GnlXN9eRHf/T/i251W4hhuxc6A92zE7G9Te2wse42bEZz/ISNCzmA3KEyFehFd3eF3GTa6Q2aAvEeUoa+t018KDLhtJwEymHixcUIZNath5oC8PXl9JTGLD6cDMjZtIfnoNq3W12CHx2usrTtiulKwpUfMh1d2JmZt/wgSLWlMjHq2uqDr0eXyIDQyKrAllw4siayw/3BM0MTpmyFijQmWNX3g7Nh9Wr+p44PwIiaWhC9OKrImsXSYia3koJ1njkzQWG8K7776D/+dnf4l//3/9O/wff/G/43e/exWJxFQm1RNY1kIZWVtPrePRzrYStulrnyHxwUdYqakmYXOS9GiI0AVxlWRtN0Si1tWG5Gc3MPHHd7Hc2IjjtXQjsU2NETccImsia+XECyVrmZ61y5S1rb112AZr8L3pddiH6IZ0fyPzm/OIrImsXSYia3koF1njEzQS6ce//Muv8dvf/gZO7iVLJtFYX4+//k//CZ/fuIHt7e1M6jSnZG09PX7ieDOFlM2K6X+9jumPPsFKbQ12fW5NGdKKqyJruyE/Up3t6tHuxFvvYJnq4WjlyTvvuC5E1kTWyg15DHqxrD16dISppfRXSz10foKpxQFKd3EdiayJrF0mImt5KBdZ26KD9vq1a/ibv/lr9IVDmbV0MG9u4b133sHf/e3fnhsgfErWcga7HqfWsG6jBuoaC9unWKvnMWwe7EVCmmKUG89d1tSjTz82TN1I3riJ8TffxlJdLQ4XT+8HkTWRtXJEZO1iWdvZ56+WasIPlt/DEq3Ezl4q8xttRNZE1i4TkbU8lIusDdFJ9ctf/AIfffCBeqtzFj6Rv/rqz/jPJHE8QzUXNWbNR7LGb5Q+NTPpcbqHzW5D8voNTH/6KVZ50oHfnZYhLUnKxPOWNfXos7tDjVGbfPd9LDfU42jp/IxckTWRtXLkRZI1HrPGL569jMegXBfJ5WHUeG7gJ+s7iM/4uSCZ32ojsiaydpmIrOWhHGSNT86O9nb8/G/+Bk0NDZm1afik+/rrry6UNa2etSzHW5tIOR1IfvZZ+pEoj2Hz8hi2i2Xpuckaj6tjUevMjFF76x2sUPqjVe19KrImslaOSM+atqzt7G/CN9KOW6bX0Bb+Hqnt/F8DKLImsnaZiKzloRxkjd8xVPXwoRqb1muxZNamYSnhx6P/7W//K0bi8czaNPlkjTneJmFz2NQYtsT7H5KwVWHnKT1sz0fWgqpHbV2NUbuBSTVGrQ5Hyxc3yCJrImvliMjaeVl79PgR5lbG0OD9Aj+Yf49Iwoq9w23MbU1heDmI2c1J9e61s4isiaxdJiJreSgXWXtw/z7+6md/eU7WFhcX8btXX8Wvf/Ur9dJWReZkLkTWGB7DlrJSg8WTDj7+FKskTrskTVrCdvmylv5/qqcLyRufqx61JUp7qPHoMxeRNZG1ckRk7bys7R/uIDxpxm3Lm2jyfYmp5UE4p9tw3flPeN/6d/jM/Wt4Z7px/Ph0OUTWRNYuE5G1PJSDrPEFt762Fj/7D/832lpbMmvT9Fp68dd/9Vf4/vtbKg9F5mS+eMzaeY431rCRHcP20SfpMWwkY2eF7VJljX7uqskEXZi5+QUm//gelpWo5a9zkTWRtXLkRZE1lp/Lec/aYyxvJNEW+g4/mP8A32gH/NNduOb4B1RFbyK64MJN9yv4NvAmtg9Ov8ZDZE1k7TIRWctDOcga46VG6m9//p/x3rvvYHV1RQnI+Pg4Xn/9NfyP//F3GBwcSCfkEzlzMitZ4561AmSNG71H25vp97Bd/wyJjz/BSh2/1oNfnPtErC5T1k4efd74HJPvvI+V5mYcrS5nyvt0RNZE1soR6Vk7LWtHxwcYTLpwx/pH1HlvIjbnx8PIDXzpfRXTqRGMLIfxqf0XqOj7BHuHp9tVkTWRtctEZC0P5SJrKZKtz69fx7/9i7/Ar/75n/HO22/jZz/7SzWxoKenRz0qVeQ04IU+Bs0lPenArl7rkfjgQ6xUV6W/6SDzWo9LkzUWtQ4StWs3MPHm2+lZnwWKGiOyJrJWjoisnZa11M4KeiIVuGV6Hd6RNowu9+OG61d42/Jz3Aq+jQ+t/xNfen6r1p/9bCJrImuXichaHspF1hj+WqmKO3fwym/+Bf/1v/wX/Jt/87/hzTffIDHJnGx8EuuUNeZoY/1kDFviw4+xWl+rvkuUH0s+c1nj7yyldfwVUvweNX70ye9RO1icz5SuMETWRNbKEZG1J7LGx/bEQgSVjg/x0PUpkitxTK3FcN3xS3xi+1/oGrmH4IwZi5sJKsM+FSyTWQaRNZG1y0RkLQ/lJGvMI2r4+D1r3MB++eUX+I//4d/j2r9+ql6I+zjbu5ahVFmj1iA96cBmRfLaZ5j+5FOsNdSrSQfrfs+zk7XmJmxQ/vzC25k/faG+lJ2/meBwgUStyAZKZE1krRwRWXNjPiNr23vrcMTq8KPlDfXVUrv7W5jfmsLXntdwJ/QBdg+3sXmwBnuiGaMrfec+27OUNY/IWmatPkTWXiLKTdZyWV9bxe0ffsA//vIXMPf0GCdrGR5tpsew8aSDJPew1dVi1WnDQOezkTVfQwOW2lowe/MLTL37AVYaG576eo6nIbImslaOiKyRrNFxfXR0qL5Oqsr1qfrC9snFKP9hNS6tffgn/NH0c3wffBc/ht7HnzyvILYUyOT0BJE1kbXLRGQtD7mytrpizAHEJ2SkPy1ry4tPf4VEoXA5x0ZGlazxiVQo3NO2srSo5OQsWyRboUBa1lLr65m1xfFoewsbLha29ItzZ+7fR6SpCZGOdqSCmfFlOmPB7YCjpgbO725hgh+9vvu+euHtcRFj1M7CwssNx/Dg0JPxfDrhV6OwrKleTAMaTIaFimWNL0SPHukvJ1/AF+fnRdbKlFxZYznRC+dwStbSq3Wh8syVNQPOv0Nq55SseTxK1jZ3VuEabsD35tdgjt7H1t6Tm9G1nXlYxmtwO/w+HkZvYmjJf+61Hcz+/uEpWTOCZ/IYlPI8JWuZ9XoQWbt8RNbycErWDOpZO3gGPWuHOT1ruwX2rOVjK6dnLZX5IvdSON5IpV/rce06Rt55D8GvvkakuUn1rO31+dXrNfTEosMK3+078Lz5Dsb/+C5W6uvOfddnsfCj4mzPmhGvDuALo9E9a5yn8T1rj6RnrYw51bNm0A3DTDJ5ImtGkZxOy9ok5WnEzdIRteOcF8vabHIaiaVB1Hiu4Xbvm4jNeOgm5fzfePToEI8eX/y3+WnGE1mbNkSC0u14XMmaUcLCT3Kysra8VPoNbC7cW3ciaxo3+qWwvrp2ImulPMnRgssmsvaSwDt4amJCnZB8Ag1GIxikxq7kiEbRHwqhs60dtVU18DidGKJ1mmkLDSpTJBxW8tdB+YYDgeLyJBEdpIvzYD/95MisD3p9aG9uQXNjEzVy3tPbFBOUZ8ThQPjHHxF6/Q2EXvkdBj78GFNffIHkl1/qjvEbN9D/h7cQ+M3vEPj8JvpN3RjI+RzFBtcdSyp/7u6OLiXqvN+00hYaA/0RuGwONNY3oNdsUcu686Rw2OzpPOliGe2j9dEB+h3nW1pwuTxOFxxWu7oI89vdhfKBZa0vEESYju8EtWvJqSlMlxi8bWJyUuXV0tBEN3VutayVttBQ5aE8gj4/2lta4KM2d2p8XFc5OSZHx+Cj8nV3dCLgc8Pir8M3bb/HvZ5P0TfoQXIycSp9kmR2htbN0E/+P5fp1O+nEpigGyQ33XxxG8mvODLis6s86ZrQ1d6hzsdkQjttMTE2MqLahzYqJ7dlLOpa6QoNLifn6aLP7rTaMELSpnf/cHC7y/unq6ND/V/3Z6fPyb2UAbqOjZBUHx0acNP9HBFZywPLGr+YsbOtgw72VnUHqTd6urpRU1WNu3cqqEFqVRdvrXTFhKm7Bw219ah+WK0Eg09OrXRPDZK93kxYeszopAbj4YNKVN67r+RSc5siwtbeDn/FXUQ++hRDb72LiQ8/wtRHn+iOsfc+QPitt+H8/E+wkmCpz24+//cLDd4f3Gg8uP8AddU1MFPdaqUrKqhOWxqbcb/iHhrr6tWyZroio6WpGQ/u3kcD5Wnu5jz1HUtmKhcfkz2d3erxllG9L8LVYG93V11o+eaLhSjo99ONSWmhtqU8WO752HE5nJSnTzNtoZEtj4fystI57KKbPM5TTzk5OA8un9XSCzflaXN2o91aDZOThNDr0txGBX0+FWfWs5wFVJ6UF7UXXAda6YoNztNJN3XcBvETDa00xUbA61U3X1Yzdzi4dZeT9wXn6aQbRZa1AB1LfHOrlbaY8Hk8sFmssNM+8hvx2elz+qmcfcEg5mZm1VODFxmRtTywrE3TXVSY7kZnppPY3dnFzvZO6bGzo7q32fZZqjjvvd097bQFBpeJx5QN0J2Yn/JdWVk1pJyLCwt0l8e9LDbMz87py5O3pQvF+tIS4nRyD5tM2BiMYn8sjr3RYR0Rx1IoAC/f3VJjnEqlsLe3r12GAoP3B08mcVCj2RcKqd6I9GffzkRu+rPrsstP1vFjaR47wWNmenssGBocUuMBef3T87h4OZvn+Ng4bFarelzLE0Ke7KP8eZxd5jy5XFOTE6p3dlYeg5YdLN88YJ8fY7G4vcyxu0c/KXj81d4un/enf19I8Lbp7Q0IOnf5ZzZPlW9m3VWMU+V8FmHQZ9/f31cTp150RNbycDJmrT9i2IBPPni4O9pCwrJE8mIEh4cHaoJBhPLlC7YRZCcY8DiC9RInGJyFhSA2FFPCwmMp0nDvTemxTvLLd7ghuoPicSRGwLLKvQ9GTTDgiyTf3fHdKE8wMEKCVJ4kVG6XS4mgEeXkcskEA0EQhKuFyFoeTmSNJOiZvLrDoNmgpby6Ix/cU8Nd3qW+ukMLLpuSNQqWViPgsrntThJL42Ttmby6Y2ZGyZrhr+5wOilPeXWHIAhCuSKylgeRtWcka6d61vTBPWsiayJrgiAI5YrIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5E1kTWRNYEQRCE54nIWh5yZW11ZTWzVh8H+/uI9KdlbXlpKbNWH1zOsZFRRML92N3dzazVx9bm5omspdbXM2v1wWWLxYYxRMLG9WAEKRLJrKxxPRgBSyXL2jBJ5TEJjBHMk/ywrE2MjyvRMgIWKpa1iXEWQP3lfExytjg/L7ImCIJwhRBZywNf/KenpkmC+rC0uEQX2UfqAlZq8Pa7JAL9oTDM3T1YoAsjX7i10hYanCf3Uo0MxxEOhbC1taW7nI9oexa0gM9HMuBSoqqZrsjgsnGv2mB0QNWD7nJSrC4vw2VzkFgGVD3or8/H2KRyekhSByNR1Vunp5y8LQvfzPQ0HL02JdXcW8d1rJW+kMjmmUxOw+VwUJ4jdKzqKyeX54iOd+4BjITDmBVZEwRBuBKIrOWBL16JySk47SQDPj9GSYhGhod1RBwD0ShMXT1oqK1HwOtTjy+10xYWo/E4YgMDsPf2orurC9H+iFqnlbbwiKtHqp3t7WhraUU4GFLrtNMWHly2XrMFlh6zErYR3eUcVj1qrU3N6GrvwBDlqb8+R1Q521vaYDWZVe+avv0eRzw2DK/LjZaGRjisNsSHYmq9dvpCIpMnCWVrcwscNhuGh6icqj5LD84jSMekhwRdyZpBPYCCIAhC6Yis5YEfLa2uLGOIZKiPhGWALuJ6Ixruh9/jhcvhRJhEY1AjTbERJbEKeL1KCCKhPs00xQb3rnjdbpUn9wSe/X0pwT2Ufionf35+tKyVptjg/eJ2uFQ5uR701idvz3XIwsJ1OmBQOXlfe5xOkn4fBg3KM+QPqHIG/T4qJ+93zldHUB6RMIl5LIbUegqiaoIgCM8fkbU88MWKHzft7e5ie2uTYkt37PDPzU01Jkzr96UG57e5YWSenBeXk/7PoZmm+OBybnHe29q/Lz7oc/Nnfwb1aeg+os978tm1fl9CqH1+qpz8U0/Q8Unl3N/bVZMNBEEQhOePyJogCIIgCMIVRmRNEARBEAThCiOyJgiCIAiCcIURWRMEQRAEQbjCiKwJgiAIgiBcYUTWBEEQBEEQrjAia4IgCIIgCFcYkTVBEARBEIQrjMiaIAiCIAjCFUZkTRAEQRAE4QojsiYIgiAIgnCFEVkTBEEQBEG4woisCYIgCIIgXGFE1gRBEARBEK4wImuCIAiCIAhXGJE1QRAEQRCEK4zImiAIgiAIwhVGZE0QBEEQBOEKI7ImCIIgCIJwhRFZEwRBEARBuMKIrAmCIAiCIFxhRNYEQRAEQRCuMCJrgiAIgiAIVxiRNUEQBEEQhCuMyJogCIIgCMIVRmRNEARBEAThCiOyJgiCIAiCcIURWRMEQRAEQbjCiKwJgiAIgiBcYUTWBEEQBEEQrjAia4IgCIIgCFcYkTVBEARBEIQrjMiaIAiCIAjCFUZkTRAEQRAE4QojsiYIgiAIgnCFEVkTBEEQBEG4woisCYIgCIIgXGFE1gRBEARBEK4wImuCIAiCIAhXGJE1QRAEQRCEK4zImiAIgiAIwpUF+P8BOsic/GoIMSQAAAAASUVORK5CYII=[/img]
1.5. As figuras que não consideraste reflexão deveram-se a que motivos? Justifica a tua resposta.
1.6. Considera o Triângulo [ABC] e a reta ED. Usando as ferramentas necessárias, constrói a imagem do triângulo segundo a reflexão do eixo ED.
1.7. Move alguns pontos do triângulo original e do eixo de simetria. Explica, justificando, o que observaste.
2. Simetria de Translação.
2.1. Visualiza o seguinte vídeo, nele encontrarás informações úteis para responder às perguntas que se seguem.
Observa o seguinte ambiente no GeoGebra onde estão representados alguns pontos e vetores. Nota que os vetores podem ser movimentados.[br]
2.2. Qual é a imagem do Ponto A pela translação associada ao vetor:
[size=100][size=150][math]\vec{v1}[/math][br][/size][/size]
[math]\vec{v2}[/math]
[math]\vec{v3}[/math]
[math]\vec{v4}[/math]
Observa a seguinte imagem:

2.3. Em quais imagens a figura A é transformada, por uma translação, na figura B?
2.4. As figuras que não consideraste translação deveram-se a que motivos? Justifica a tua resposta.
2.5. Usando as ferramentas necessárias, desenha o pentágono [A'B'C'D'E'] transformado do pentágono [ABCDE] pela translação associada ao vetor [math]\vec{u}[/math].
2.6. Na translação anterior, compara o segmento de reta AB com o seu transforado A'B'. Comenta o que observas.
2.7.Numa simetria de translação o que podemos afirmar sobre os ângulos das figuras? Justifica a tua resposta.
2.8. Na figura anterior, usando a ferramenta adequada, cria um novo vetor. A partir do pentágono [A'B'C'D'E'] constrói o seu transformado [A''B''C''D''E''] pela translação segundo o novo vetor criado. Descreve a relação entre o pentágono original [ABCDE] e o pentágono final.
3. Simetria de Reflexão Deslizante.
3.1. Observa o seguinte vídeo e responde às perguntas que se seguem.
3.2. Numa Simetria de Reflexão Deslizante de eixo r e vetor [math]\vec{u}[/math]:
3.3. Numa simetria de reflexão deslizante a distância de um ponto ao eixo é igual à distância da imagem desse ponto ao eixo.
Observa a seguinte imagem:
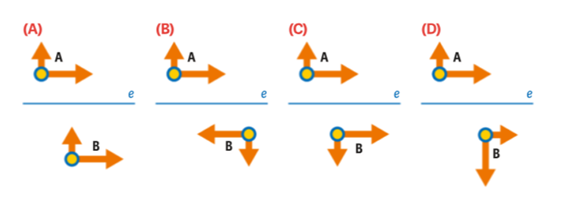
3.4. Em qual das opções, a figura B é obtida da figura A, por uma reflexão deslizante de eixo e?
3.5. Utilizando as ferramentas necessárias, constrói a imagem do polígono [ABCD] pela reflexão deslizante de eixo [math]\vec{u}[/math].
Considera as figuras 1 e 2 representadas na grelha abaixo:
3.6. A partir das isometrias de reflexão e translação, consegues utilizá-las de modo a obter a figura 2 a partir da figura 1? Em caso afirmativo, descreve como procederias.