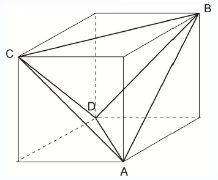
Tetraedro inscrito em um cubo

O [b]cubo[/b] é uma figura que faz parte da geometria espacial. É caracterizado como um [b]poliedro[/b] (hexaedro) regular ou ainda, um [b]paralelepípedo retângulo[/b] com todas as faces e arestas congruentes e perpendiculares (a = b = c).[br][img width=280,height=311]https://static.todamateria.com.br/upload/55/6c/556c7dfb203ea-cubo.jpg[/img]Tal como o tetraedro, o octaedro, o dodecaedro e o icosaedro é considerado um dos “Sólidos de Platão” (sólidos formados por faces, arestas e vértices). O cubo é formado por 12 arestas (segmentos de retas) congruentes, 6 faces quadrangulares e 8 vértices (pontos).Diagonais do CuboAs linhas diagonais são segmentos de reta entre dois vértices e, no caso do cubo tem-se:[b]Diagonal Lateral[/b]: d = a√2[br][b]Diagonal do Cubo[/b]: d = a√3Área do CuboA área corresponde a quantidade de espaço (superfície) necessária para determinado objeto. Nesse caso, para calcular a [b]área total do cubo[/b], que possui 6 faces, utilizamos a seguinte fórmula:[b]A[sub]t[/sub] = 6a[sup]2[/sup][/b] Sendo,[b] A[sub]t[/sub][/b]: área totale[b] a[/b]: aresta.Para tanto, a[b] área lateral do cubo[/b], ou seja, a soma das áreas dos quatro quadrados que formam esse poliedro regular, é calculada a partir da fórmula abaixo:[b]A[sub]l[/sub] = 4a[sup]2[/sup][/b] Sendo,[b] A[sub]l[/sub][/b]: área lateral e[b] a[/b]: aresta.Além disso, é possível calcular a [b]área da base do cubo[/b], dada pela fórmula:[b]A[sub]b[/sub] = a[sup]2[/sup][/b] Sendo,[b] A[sub]b[/sub][/b]: área da base e[b] a[/b]: aresta.Volume do CuboO volume de uma figura geométrica corresponde ao espaço ocupado por determinado objeto. Assim, para calcular o volume do cubo utiliza-se a fórmula:[b]V = a[sup]3[/sup][/b] Sendo,[b] V[/b]: volume do cuboe[b] a[/b]: aresta[br][right][/right]O tetraedro regular é uma pirâmide regular que apresenta as quatro faces congruentes e as seis arestas também congruentes.[br][br][img]https://static.mundoeducacao.uol.com.br/mundoeducacao/conteudo/tetraedro2.JPG[/img][br][b]Cálculo da área total do tetraedro.[/b][br][br]Como o tetraedro regular é composto por 4 faces triangulares e os [br]triângulos das faces são equiláteros, a área total será dada por:[br][br][img]https://static.mundoeducacao.uol.com.br/mundoeducacao/conteudo/tetra.gif[/img][br]O elemento[b] ([/b][b][i]a) [/i][/b]na fórmula descrita acima é a medida da aresta do tetraedro.[br]Para determinação à altura do tetraedro utilizamos a seguinte formulação:[br][br][img]https://static.mundoeducacao.uol.com.br/mundoeducacao/conteudo/tetra1.gif[/img][br][b]Cálculo do volume do tetraedro[/b][br][br]O volume do tetraedro, assim como o de qualquer pirâmide, é obtido fazendo:[br][br][img]https://static.mundoeducacao.uol.com.br/mundoeducacao/conteudo/tetra2.gif[/img][br][br]Onde, S[sub]B[/sub] → é a área da base do tetraedro.[br]Como,[img]https://static.mundoeducacao.uol.com.br/mundoeducacao/conteudo/tetra3.gif[/img] e[img]https://static.mundoeducacao.uol.com.br/mundoeducacao/conteudo/tetra4.gif[/img][br][br]Obtemos: [img]https://static.mundoeducacao.uol.com.br/mundoeducacao/conteudo/tetra5.gif[/img]ou [img]https://static.mundoeducacao.uol.com.br/mundoeducacao/conteudo/tetra6.gif[/img][br][br]