Função de 1º Grau ou Função Afim
Definição
Uma [b]função de 1º grau [/b]ou[b] função afim[/b] é uma função [math]f:\mathbb{R}\longrightarrow\mathbb{R}[/math] dada por[br][math]f\left(x\right)=ax+b[/math] para todo [math]x[/math] real, em que [math]a[/math] e [math]b[/math] são números reais dados e [math]a=0[/math].[br]Caso tivéssemos [math]a=0[/math] e [math]b[/math] um número real qualquer, a função se tornaria[br][math]f\left(x\right)=b[/math]. Tal função é denominada de [b]função constante[/b].
Exemplo de Funções Afim
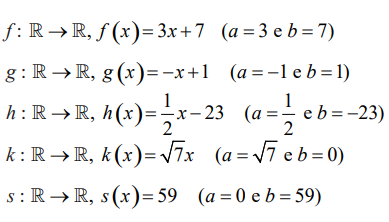
Responda as questões
1)
Qual é o valor de [math]f(3)[/math] para a função afim [math]f(x)=2x+1[/math]
2)
A função [math]f(x)=ax+b[/math] passa pelos pontos [math](1,3)[/math] e [math](3,7)[/math]. Quais são os valores de [b][math]a[/math][/b] e [math]b[/math]
3)
A função afim [math]f(x)=ax+b[/math] é tal que seu gráfico intersecta o eixo [math]y[/math] no ponto [math](0,−4)[/math] e é perpendicular à reta [math]g(x)=\frac{1}{2}x+1[/math]. Qual é a expressão de [math]f(x)[/math]?