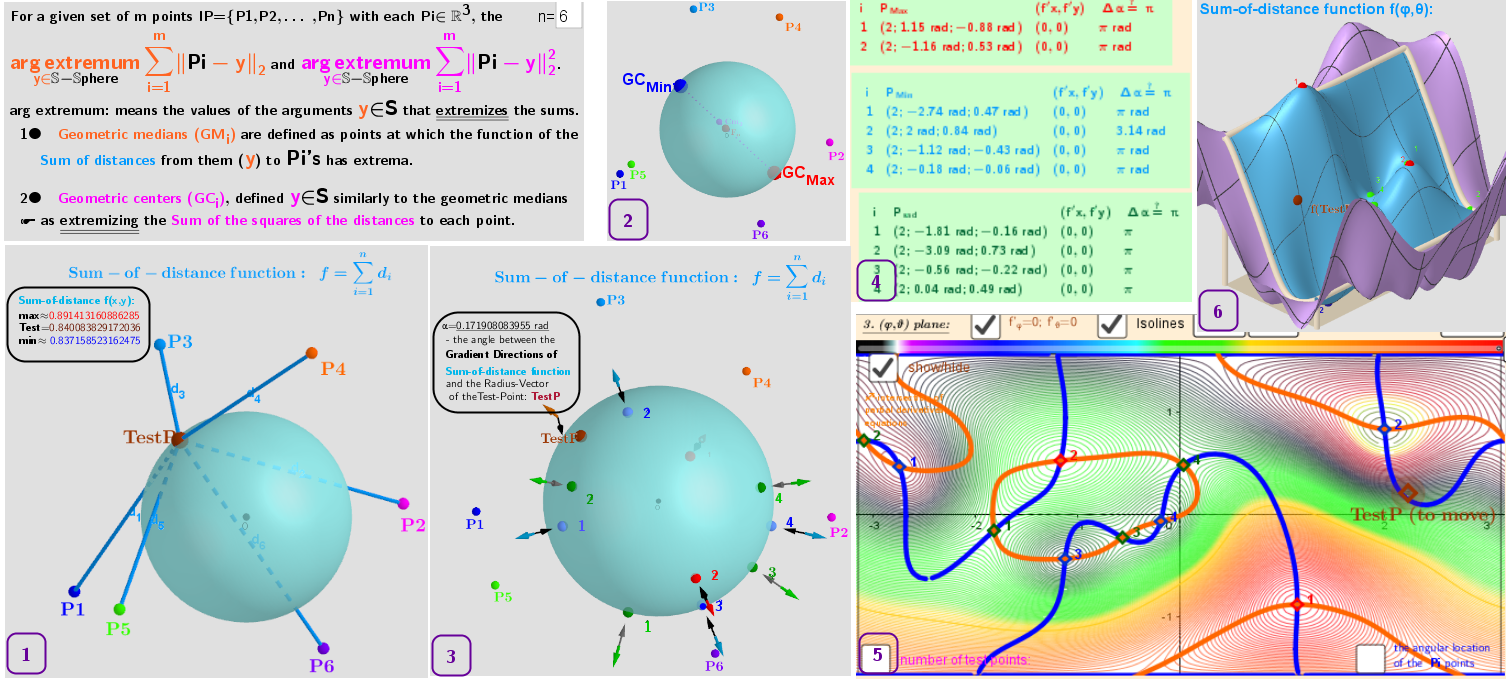
[size=85][color=#9900ff][b]1[/b][/color]. 6 Points in ℝ³ and the search their [b]Point Estimators[/b]: [i]geometric [color=#ff7700]medians[/color][/i] and [i]geometric [color=#ff00ff]centers[/color][/i] on the surface of the sphere.[br][color=#9900ff][b]2[/b][/color]. Regardless of the number of points they have only two geometric [color=#ff00ff]centers[/color] on the surface of the sphere: two antipodal points.[br][color=#9900ff][b]3[/b][/color]. The existing distribution of 6 points in this example give ten geometric [color=#ff7700]medians[/color] on the surface of the sphere: 2 [color=#ff0000]maxima[/color], 4 [color=#0000ff]minima[/color] and 4 [color=#38761d]saddle[/color] critical points for the [i]sum-distance function[/i]. The vectors ∇f and ∇g are parallel at these points.[br][b][color=#9900ff]4[/color][/b]. Table of coordinates of the critical points of [color=#1e84cc]distance sum-distance function [/color]f(φ,θ) over a rectangular region φ∈[-π,π], θ∈[-0.5π,0.5π] on the surface of the sphere. They are found using [i]Lagrange multipliers[/i] as finding the Extreme values of the function f(x,y,z) subject to a g(x,y,z)=0 (constraining equation: g(x,y,z)=x²+y²+z²-R²). The table also contains partial derivatives and Angles between the vectors ∇f and ∇g at these critical points.[br][b][color=#9900ff]5[/color][/b]. (φ;θ) -plane of the angular coordinates of points on the sphere. The colored Isolines are qualitatively indicate the type of critical points. The intersection of implicit functions of the equations of zero partial derivatives: f'[sub]φ[/sub](φ, θ)=0; f'[sub]θ[/sub](φ,θ)=0 over a rectangular region φ∈[-π,π], θ∈[-0.5π,0.5π] -are solutions (critical points) of the Lagrange equations.[br][b][color=#9900ff]6[/color][/b]. Graphic of the distance sum function f(φ, θ) over a rectangular region φ∈[-π,π], θ∈[-0.5π,0.5π] with the positions of the corresponding [color=#ff0000]maxima[/color]/[color=#0000ff]minima[/color] and [color=#38761d]saddles[/color] -its critical points.[/size][br]