[br][justify] Os números reais apresentam-se como um tipo de número que mensura o espaço em nossa volta, assim como a concepção de número em seu conceito geral possibilitou, desde muito tempo, que o ser humano mensurasse a matéria, a energia, e outros componentes mensuráveis de nosso universo. [br] Os[b] [/b][b]números irracionais[/b] são números reais que não podem ser escritos em formato de fração, ou seja, [b]não é racional[/b]. Seu conceito envolve alguns detalhes muito interessantes que não podem ser interpretados meramente por uma perspectiva voltada à números racionais.[br] O entendimento de que as frações não são suficientes para as atribuições de medidas foi descoberto há 2500 anos pelos gregos. Eles perceberam que a diagonal de um quadrado de lado um, não pode ser expresso por nenhum número racional. Atualmente é dito que a medida dessa diagonal é a raiz quadrada de 2, sendo este fato garantido pelo Teorema de Pitágoras (Ver imagem seguinte).[/justify]

A reta numérica serve para a representação de várias grandezas escalares. Uma delas são os [b]números inteiros[/b]. [br]Esta construção ilustra como como representar os números inteiros no sistema de representação chamado de reta numérica. [br]Representar números na reta numérica significa graduar a reta. [br]Esta é uma ação muito comum quando lidamos com grandezas escalares como temperatura, comprimento, posição, massa, etc.[br]A partir da construção abaixo, você poderá perceber como graduar a reta através da unidade de medida estabelecida.[br]

[b]Problema:[/b][br]Achar a medida da hipotenusa "AB" de um triângulo retângulo isósceles tomando um cateto como unidade de medida. [br]Admite-se que este triângulo tenha lado igual a 1 unidade.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUcAAAFKCAYAAACO1521AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAEw1SURBVHhe7Z0FeJRn1oaz291uV/6Vure0hVKgQNGQQAhS3KVAS5HgVPDSUkEqUKRAcUiCu8VwDRQnBIfgGuLu9vzvOe83SYABEiDJyLn3eq4JzGS6TGaenPMdeR0gCIIg3IWYoyAIghnEHAVBEMwg5igIgmAGMUdBEAQziDkKgiCYQcxREATBDGKOgiAIZhBzFARBMIOYoyAIghnEHAVBEMwg5igIgmAGMUdBEAQziDkKgiCYQcxREATBDGKOdxAWBuzcCXh5AT4+wPr1wPnzxp2CINgNYo65yMwEdu8GevcG6tUDGjYEWrcG5s8HEhKMBwmCYBeIORpkZemocckSoFUroGJFoFIlwMUF+PlnICgISEszHiwIgs0j5miQkQEEBgK//gq0bQs0a6ZNkm4HDAA2bABiYowHC4Jg84g5GqSmAuvWAX36AC1aAP37A999B3ToALRvD0yfDty8aTxYEASbR8zRICkJmD0bqF8faNIEmDdPR4t0/bFGDeCrr3RqLQiCfSDmqKBCzI0bwE8/AdWr62hxzx7g2jVg+HCgWjXAzQ344w+57igI9oKYoyI+Hti1S19bpAr10KHA6dNAZCTg7q7T7I8/BhYtAm7dMr5JEASbRsxRQVHj3LlAp07aBGfOBIKDgcREYNMm4LPPgDZtgB9/1EUbijQFQbBtxBwVJ08C338PNGoEfPGFjiJNBnjlCjB2rK5ad+2qizZU2RYEwbYRc1RQ43fnzoCTE/Dtt8CFC8YdipQUXZwh4/zwQ51mJycbdwqCYLPYtTlS43dcHLBqle5pJHPs2xdYsECPDnp7a40cCTRooBvCR48Grl+X6FEQbB27Nsf0dODMGWDSJKBlS8DVVZsgRYkmNW6sizR16ujIkVp6KO2mIo4gCLaLXZsj9TZu2aINr3lzoHZtbZAUQTo65oj6HGvV0j2QPXroWWtpCBcE28auzTE2FvDw0JXopk11MWbCBOC33+4WTcu0a6ejSSreUMQpCILtYtfmSO061J7j7KyNb+1afQ2SUuY7dfQoMGSIjiqpak1N4nTNUhAE28RuzZGq0IcP6xlqSqXplgzwXtDSialTdWpNiylWrpRFFIJgy9itOYaGAitW6Cjwo4/0YomrV407zUD7HKnHsVcvnYaPG6dTa6laC4JtYrfmePy4nqWm0UC61rh9u06f74Wpsj1mjK5s0/YeWkxBRR1BEGwPuzVHMja6zkjXG0eN0r2LDxoLpOhx6VK9tadmTd0CFB1t3CkIgk1ht+bo7w98/TXQr58+L4auQeaFI0eAESP0KjNqFqeKtyAItofdmiNFfJcuARcvAlFRxl/mAVpGQavMzp3TG3oo3RYEwfawW3MUBEG4H2KOgiAIZhBzFARBMIOYoyAIghls1hwzMtKQkpKEpKR4vs3MlG5tQRDyjk2aY2xsNAIDD2PTJj+sWbOMb0+fPoHU1Dz26wiCYPfYlDlevHgevr6r8dtvYzBw4Ffo0qU/2rf/Al279sewYd9jxozfsXPnZoSHhxrfIQiCYB6bMEdKmYOCTuOXX0ajWrU6KFasMt59tyVKlx6AsmWH4/33+6mvW+Odd6qiSZPWWLx4kTLIMOO7BUEQ7sYmzPHkyUAMGfK5MsIP8dprvZU5jleGuByVKu1E1aqHULnyDv7z66//rO7/GLVrN8Hs2ZMlghQE4Z5YvTlevHgOP/74k4oUnfH88z1Qo0YgL66lzd4kOjXQdNuoUbIyUC88+2wL1KnTDIsWLURkZLjxTIIgCDlYvTl6es5ExYr1VbQ4CI6O+9C4cRpv2jGZY27R33/4YTTKl/dWEWQHlWK3xM6dm4xnEgRByMFqzTErKxMhIbcwYMBnKhKspiLCNdmmSFEiRY93ymSQDRsmKnMcgRIlqmLGjMmIjqbhalnrLQhCDlZrjsnJCfD334GOHbvgjTc6qKjxMB+vei9jNMlknmXKLMb777fGsGHf4cSJo9IHKQjCbVitOUZEhGDBgnkqje6mIsBvUaPGeV5Cm1dzrFhxm4o2+6F79wHYunUD0tKkB1IQhBys1hxv3ryKKVMmo27dXihdeiJq1rzCKXNezJFuK1feh3LlhuOTT76At/dKnqIRBEEwYbXmGBYWDE/POWjYsDtKlhwFF5cL+Yocqc2nXLnB3CC+aZMvUlOTjWcWBEGwYnNMSIhTprYB7dp1QbFiXeHkdDRf1xzLlVul0uqPMXjwNwgIOICMDNlaKwhCDlZrjlRAuXLlMj7/vBeee84F5cuv48jRZH7mjJH+nlLvRo3TUOzt8XivTG38PnUywrgZXKrVgiDkYLXmSGRkZGDy5HF4911XFC/+E1xdz6NJk6xsg7xT3MbTKBXVnA7g5Rc7walKdfh6r0SWnM4vCMIdWLU5ErR9p1+/wcoc6+PVV39QBnmZzbGlSrEpkiRDpFtSU2WQVavtxyuvfYb3XiyBgW0+xNFtXioMlZRaEITbsXpzTE9Pw549O9GtW2e8805DvPXWKJQp46Wiw4NwUZGka+1r6jYIjk77Ufr9FXjj1b4o8fzb+LTC81jyWWMcXzgOkWcOIyNFCjKCIORg9eZIJCcnYu/e3fjii0EqgnTC8885oVixjihZ8nuULj1O3Q5TpvkxXnrFBeWKl0efWuXg+Wk1rPu8HrYNbY2jc39B+JkAMUhBELKxCXMk6Prj4cP7MXHiaPTt2Rkt6tZD9VLVUKlYFdQsWwNtGjVCv77dMPXX77Btxijs/bkn1vepDW83J2we0hqB88awQWampRrPKAiCPWMz5miCJl1OBx7AgjFfY2jjCuhZ6UV836YGlk0aiaCAvYgPu47YSycRtHY2dgzvDL8+deHTvTo2D26JYwvGIeLMEaRLQ7gg2D02Z45EclQIjq+Zg9VfNIRnm1Lw/eYjnN6wCAnBl4GkWKTHhCMyKBBnveYog+wEn27V4du7FrZ81QZH5/2K8NNyDVIQ7B2bNMe02HBc2bwUu4a1w3o3R+wb3R03dq1Fwq0ryjjDkBITgeToMEScO4ozq2Zgxw+d4NvTFV5dq2HLUDLIMQg7dVAMUhDsGBuNHENxfv0ibB3aFms7V4b/j264vH0V4m5eRFJECJIiQ5EUFY7E8GBEqAjyNBnk9x3h17s2fHrWVCl2CxydryLIM4clxRYEO8UmzTEpMgTn1i3kNHlNp8rYOaorLm1bidgbJnNUUrfJyiDpNuJsAM7QNUgVQXpTiq0M0hRBcootc9eCYHfYrTlS1JgUcUtFkGEcaUZSir1aRZDDO6kIshan2JuHtOIqtk6xJYIUBHvCrs2RpQySrkPS12yQHEF+Ct9etZRcsXFgcwTOHc0pthikINgPYo5K/HfKIOlaZMTZIzirDHLniC7w6V4D3tTm81VrlWKTQUofpCDYC2KOJhkpNt0Xef44zqxRBmn0QXq56RT76IKxRpuPRJCCYOuIOd5hkDkp9jEVQc7hFNunhwt8e9fG5sHKIHmSRqrYgmDriDneIb4/moo0YZxic5sPVbFViu3l5qyr2POpin1IqtiCYMOIOZqTkWInRuTqg1QRpF+fOsoknTnFPraAJmkOqQhSDFIQbBExx3tJPY6maOhrMkhKsXcqg6QIklPsr4wUW0WXGalycqEg2BpijvcRPZbSazJJbvNZMws7R3TmKRrug/yqNQLnyqihINgiYo55EFexVaodeYGq2LOw/XuVYvdWKXaPGtg4sJnug5QqtiDYFGKOeZCOIMP5+yiNPr16ZnaRxqenq27zUREkFXAkxRYE20DMMY8yjRqaGsXJIKlRnJZVeHV15P/WsQVjEUZVbIkgBcHqEXPMj8ggjSJN5PljetRQpdh61LAWL8wNpEkarmKLQQqCNSPmmE/R91KBJikq9PYUu1t1bhbXRRptkNIHKQjWi5jjQ8iUYieq59F9kCrFpm0+fepkb/PR687EIAXBWhFzfFiZDFJ9TW0+plFD2iiuRw1b6oW5KrpMT5UUWxCsDTHHRxA/V3S4UiifSaOXVehtPnQuzWb13w/0HK37ICWCFASrQszxUWWqYqvbqHPHcIauQVIfJKfYTtg0sAUCeRZb+iAFwZoQc3wcUsbIfZDqa2rzObN6FhdpfLrTNp9a2DxEpdjZo4YSQQqCNSDm+JhEz0ujhlTFZoOkFHtEVz6PxsvNONWQrkGekiKNIFgDYo6PVUaRRkWSemGuiiCNUUOfHjV0kYbPxT6E9GRJsQXBkhFzfMziCJKKNMogs1NsZZA+3avrFJu2+cz9Ra5BCoKFI+ZYACJjzEmxA7lIQ6OGNEWjRw1b88LcME6xZRZbECwRMccCU65RQz5yQY8a0rGvvr1qYvOQFvoa5JkjMmooCBaImGMBiv47HEGqW4ogeWHu8M46xe5JBtkKgZ6/GBGkFGkEwZIQcyxgZW/zUSk2LaugUUNq86EizdrOVbFpUAsEziWDlEZxQbAkxBwLQ3QN0kix9TVI3Qept/m4GgtzjT5ISbEFwSIQcywk0X+TI0h1S1Xss2tmw39kV24Up40+m4e25kZxSbEFwTIQcyxMmVLsyFBE0T5I6oMc3hl+fepyo7hpkoZSbCnSCELRIuZY2OI2n3D+mtedqQiStvn49KRRw9pskHQNUhbmCkLRIuZYBOL/D7kW5mafaqhSbK9uTnrUkDeKH0ZmWqrxrxIEoTARcywqmVJs9f8ne9RQRZC0zYevQQ6mPsixCD9zWEWQcg1SEAobMcciFE/SUASpbinFpkZx3QdZgyvZm+hMGk+VYp+RbT6CUNiIORaxckYNwxBxzhg1VAZJG8XXdnHkRnGapOFTDWXUUBAKDTFHC1GSqUhz7qgySCrS6DNpqFCziVNsGjUMkCKNIBQSYo4WIvr/RRFkorqNUGk07YPcMbwTvGnUsFdN9W/JdaqhXIMUhAJHzNGCZDJI6oPkNp+VM/QkTW+9zYeOfTU1iksEKQgFi5ijpYmq2KZRw6CjOG3sgySDpCINV7HJIE8fRnpyovEvFgThcSPmaIGi/39skOqW+iBp1JD2QdKJhj49XHL6IM8cRob0QQpCgSDmaKky9UHmGjWkKrbpVEPeKM5FGmWQ0uYjCI8dMUdLltHmkxgRzOvOznq562uQPWryqCH1QdJGce6DlCKNIDxWxBwtXPz/V6XY1CxORRrug/xBN4p7uTlnp9iyzUcQHi9ijtYgI8WmWy7SrJqhj1zgUUPnnCKNbPMRhMeGmKO1yJRiq69pHyRXsVWKzaOGlGLTRnGPn3mSRgxSEB4dMUcrUu5TDU3bfPypis2jhtVUBNkKRzx/RujJA0iXFFsQHgkxRyuUKcWOOn+cD+3ihbl968JbRZH6yIVfjAhS+iAF4WERc7RC0b+BFuYmReprkFzFHtFVmaMLfHq5GgtzqQ8yABlpsqxCEB4GMUcrlT7VMJQr2dTmc4aOfVUG6de7No8a0iy23uYjRRpBeBjEHK1axqihMkpemEv7IGmbD48aqghyEFWxqc1HGaSMGgpCvhBztHLRv8W0rILSaD72lbb5mEYNeZuPnIstCPlFzNEGpFNsZZDq36b3QRqjhpxi06mGrXIiSEmxBSFPiDnaigyDpK8jz9Go4Rw+k4Y2itNGH1qYm13FlhRbEB6ImKMNif9t0eFskpE0akjXIKkPsnsNTrOzU2xlkHKqoSDcHzFHW5MpxVb/xsgLdKqhPrTLr09deLk5cZsPb/M5HSDLKgThPog52qKUQXIfpPo6QqXYQd4eKsXuzAUaGjVkg5w3hg1SJmkEwTxijjYq+nfqUcNwLtLwLLaKIMkgOYJUrw0d+xoqVWxBMIuYo03LKNJE6Ajy9KqZ2M7bfOryNciNA5riiDJI6YMUhLsRc7RxcQRpNIrTqYan+VRDiiBrcKM4bfM54vGT7oOUa5CCkI2Yox0oe5uPcaohF2lGduXrj2u7VOWN4rTNJ+ykpNiCYELM0Y7EVWx1S1VsWlZBbT68MLeHi0qxaZuPcWhXsjSKC4KYox2J/t16m08o90FSFdt/RFfug/TpUZMnaagPUrb5CIKYo93JNGqYHEWnGh43ZrFNo4aO2acaUqN4howaCnaMmKM9igySijTqaz6TZo0yyO8/5QINjRrymTSUYsuooWDHiDnaqeg1ME3S8JELRgRJ28QpzabX7qhpm49UsQU7RMzRnmWk2PR6UATJx76OuGPUkE41pDNp7KRIQ1uLQk/sx6Wt3uo9o6Wr+Pe+BhsXfAVXd/vx91zxNycfXNnly4+5cXAbLwZJjgk3vluwVMQc7V3c5hPOX0eeO4ogb3fsHN6JCzQ8akjbfLhR3D5ONYy+fAZbv2kPj+ovY25NJZdXuHE+5tp54xF3c279QixtWRye1V/BwvovY8GHLyg9n62F9V/kv1/c+HWs/qQCdo50Q5DvfMRev4CszAzjWQRLQ8xRpF+TaCrShLFB0qFdvM2HRg27OavXsbU2yNP3j6CsnbTEOFzavgbLW72LX59xwNhnlZ5zwIq2ZVT054v0pHjjkbdzYskkTHtfPVZ9z2+vOeBX9X2/Pp1L6u/p78Y+74BJbznAw+n/sOrjqjg08zueXJLOAMtEzFGkxSl2qHp9biHqwgltkFTFplMNlUHSPsij82lZxWGbjSBjrp5ThvWDivBew/T3/4zZlZ7C9LJ/xtKmbyJgziiO9MxxevUMuFd7CpPedMC8Wk9jzaeV4eXmfIecQMfnLm/zHjyc/4OppRywpEkx9bw/8vtSsDzEHEU5ohRbRZBkkLSsghvF6ciF7jWMbT6tdBWb+iBtMIK8eXAbz5t7OP0dCxu8qgytOhbUewmezv/A5sEtERyw03jk7ZxePRNzqvwF419y4Kb6m4d3ql8wJ3PpBIsKX5SCb/26HTxr/BvTSv8JXsowr+/daDyTYEmIOYpuU/aoYXQ4p9hUpKEqNm0U5yMXvqJG8dEIpSKFjVWxz/nNx6KGr+D3Eg5Y/2UDnFw+Bev61uE/L2n8Os5vWGI88nbIHGdX+jOnzXS9MjMtzbjnbmg88/r+TfxakpnOrfEv/u8KloeYo8iscrb5GH2QfKohjRrW0KOGxix2epIt9EFmsWlR6jyrgoMywydwYMrXKs0Owr7fBmBy8Scwq9Kf1L95ND+OHp8bNsfKT2CcMsctX3+EtMQE4x7zRF08xZH4+BcdsKDuc7iwaalxj2BJiDmKzIpeJ4ogE9Ut90HyRnFdpPFRUSRv83H/Ube5WPk1yIy0VEScDcT27zpiVkUHzKv9Mv97U2IjcWrlNMyt/RKbI0XQVEDJTL89MsxtjpuHtkFqXIxxz93EB1/GyWVTsKxFccwo9xes61NXpeHbjXsFS0LMUXRPZafYUbTN5yjOKsPwH+nGEaTe5qPbfMJPHrDqFDslLgpnvT2xpuMHcHf6O5/7fWP/FqQlxePa3g3w7VWT/35t50o4t34R0hJije/U8DVHxyfx26sOWNWhHL8mJ1dMvUvHl0zCnl/7wauLI5Y0eRMbvqyPIO+5SAi9bjyTYEmIOYruL2WQplHDKNrmQ0cuqAiSZrH1PsjmxqjhYattFI+/dQ17JvSHZ43/qqjxaRz4/SskhN0w7ruK/ZMGYV6t/2FuzWc53U4Mu8n3mSBz9Kj+T/z+jgNHnvfTtDIOKsr8szLiSjilDDM5OsJ4FsHSEHMUPVD0epFBmvZBmtad6W0+Lvw66zNpDltlFZuuAfp9Vg8T3/wTFjZ89a5rgOc3LsbC+i9hUrE/Y0O/Jtzykxs2xxr/wpQSyvxKOWDCKw4Y9+LdomuM417Qj1nTqQq/RzMzpAncUhFzFOVNFEFSik3rzoxtPvpUwzq6ik1tPrTNh45csKJrkFRgubZnA1a0KcXV43m1VXT4+1D1flmFi1tW8O1+FUlS/yLdv7J9OR4BzH20LZmju5Puc6Rq98b+TbFlaFuz8u1ZF8taFseyVu9i1+heCDm6B2mJ5pvLhaJFzFGUdxnXIOlrnsVeO5ur2L49TaOGLXUV24rOpIkPvoJAFfUubvQqp8UzyjlwisxptKtKs9Ut/Zn+frK6f0mzYji+dBISQnXaTXBBhvocVWS4/stG6pfHCd1Qb0Yhx/Zyar6kaTEsbPAK9o0fgCj1eMHyEHMU5Uv8+hkRJFWxT6/OOZOGDu3abBo1pGUVVnDkQvCRXdj+fUfMU0ZIafGkYir9VREijwAaoj/T2B/1O86v8wz8f+zGJmeCzdHoc9zyTTsVjeZElea4FbgbazpXxWT1nKs+KoOru/yMewRLQsxRlH8ZKTbdUmuLKcVeRyl2Nye9rGLuaGPdmWWn2EG+87CibVnM/OAJlVK/yKN+XGzKJb0I2FlFkS9gZoW/YFWHD3B+/WLjGQxzpFaeFxz4PB5qf7ofFH1vHNicW388VVR6zm+BcY9gSYg5ih5O2Sn2LV7BlbPNR48akknoIxcOW2ybT2ZGGs9Sz/zgSUwtSdMtHRB6fB9ir52/S6HH9mHL0I8w5V0HFSX+DUfcfzKe5Q5zHNKKf3HcDyrorP+iAT+ezDFIJmQsEjFH0UPL1AdJ89i8zYcaxUd04WuQVKSh119XsQ9ZXBWbVoXF3ryIHcM/xdT3HODu/D8cXTjWuNc8gfNGw93xP5hW2gH+o9z430+cWTuHzTEv44NxwZdxYulkLG/9Lia/7YClzYrh0taVxr2CJSHmKHpkmVJsPpPGKNJQFZtafTYPaqEX5lpYH2RqYiwu7VgN725OmFPlCY54L+/0Mu41z6Xtq1XaXY2XTNDjbxzYgqyMDJWaz4V71Sf52iRFzdRAThM3dyr48E4+And1x0oqWlWGXO1JbBvWnpfrCpaHmKPo0UURpGmbD48azmGDJHPUjeItcMTjZ4vqg6QI7tCM73gZLRVZ9k8ejJjLZ417zRN98RT2TPiSK9i0wPbYgnFIiYnkTTsezv/gVp65Nf+Dle3LYk3HindpVftyWNTwVcyq8BeOVld3rMBLJ+g5BMtDzFH0WETGyFXsKD1qSNfhOMXuVQtrO1fVbT4qLQ0/RacaFv01yFtH96jU34mX09IoH/U0PmiJRnpiPI8PUkM4fd+GLxpyAzldM5xRXi/H5WW3zzhgzNO3i5be0jVGura5oO7LKsKsx+l1fMg149kFS0PMUfQYRQapj1zgKvYaI8VWqaZPz5p61NCYpCnqPkhqxVn3WT0V6b2J7d9+wlFhXqB/12b1vvKs8aYy/Nbc03j1j3VY2aGciiiLsdEubvTa3Wr8Opa1KsHXY/dNGqy+x49/kQiWi5ij6LGKXlteVqFeZ06x1+oiDY8aKmMwHbkQeupAkU7SJEeH8zXAKzs36OW9efz/QqZO5+lc3rEBtwL/QEpcNP9baWrm6u6NvLjWrPZtUo/ZyqYcc+0cL7UQLBsxR9FjV3aKTbPYvDCX+iD1sgqvro58qiG1+VAhQs7FFiwVMUdRwYgM0tjmw6OGRopNBRrf3rW4SMOTNFY0aijYF2KOogITvc7ZRZqzgdmnGtKZNLlHDbkPUk7gEywMMUdRwSpXis2nGlKjuGmbjxuNGrbkUw3DyCBt7EwawboRcxQVvJRBJkeFI0l9TaOGZ7082CBpFyQ1TetZbBo1DLDZY18F60PMUVQootedq9jGqGHuM2k4ghyqUmxaVmHlRy4ItoOYo6gQZaTYKpKkCPIMrzvTo4be3atzHyTvgzxxAOlJ9z/BTxAKGjFHUeGKIkiqYiuD1KOG2iD1Nh+qYjfnjTd63ZlEkELRIeYoKnRR5MgpNo8aBiqDnAX/kV2zRw3pVMMjHj/pPki5BikUEWKOoiITp9gq1aYqdpCXO3aM6KJTbBVFbhzQTKfY0gcpFBFijqIiE/0suIpNh3bRPkhvD+wc6WacauiqJ2m4Udzy9kEKto+Yo6hIZRo1TFYpNp1qSMe++iuD9Otdhw+/p0ZxOhc77CSdaigRpFB4iDmKil6GQdLX3CjOfZA0aliLpavYFEEeQJqk2EIhIeYosgjxz+WOIg03inerzpVsPWr4M0JVBElnTQtCQfPI5khv7PCzAbwy/spOb2VCq3HF3xs3D27jNzmlS/mFDiC6vGMtLmxejQubVuPanvVICLtp3PtgxBytVEYEST8f3uZjGCSfati1ml6YazSKS5FGKGge2hwzM9J5C/LJ5VP53N/VHStiUYNXMb/WM7wKfm3nKtgxojPOersj7uYlPtAoL1BUcGzheH4OD+cX4O70Ala1L6uMcjmQlWU86v6IOVqxjDYf+jry/DGuYu9U7yPfHjV51FC2+QiFxUOZY2p8DC5tXcWVxRUfvY85VZ/ik9ToHF7TOng6AN2j+r+w+pOK2D26Dy/8zEy/96lsBN0fdek0r7ai5zOtm59VwQEHp3+HxNAbyh8fbJBijtYt/hlF5zrVkIo0I7rqUcNuztkpNhVppIotFBT5NseU2ChcVFHcuj4fYlZFBz47Y8GHLykTrMCrqOgN7O3mjBVtS8PT5T+YVsoBs6s8wavlr+/fon7b37upl0z3/IYl8O3pws89q8JTmFn+SXg4PYWtQ9vwqW4ZaanGo++NmKMNiFPsUP5ZcZFm7RxlkJ3h17cuv782DaYjF1SKzdt8pFFcePzk2xyv7PKFX5+6cHd8iiO6Ve3K4sCUr3kNPEV90VfO8rXG8xsXc7q9oO7zmF7WQaXH/8SWb9rxEZ33IiHkmnquoVhU/2U+7HxNJ0esbFcO7tX+hhWt3+MDidIS4oxH3xsxRxsRpdgqeuRZbEqxqQ+SijTdc23zUREkn2ooo4bCYybP5kjXGONuXsbe3waqNPpvbHi+vWojyHceoi+fMR6VAy0OuHX0DxxS6fCSZm9hUjEVYdZ7kQ2OFhCYu35I1zA39GuE34s/gUUNXkbgvDHYP3kI5jg+iell/sHpeUp0hPHoeyPmaDsyjRrSmS+87oy2+dCphj1d+QzpzUNa8bGvNGooEaTwOMmzOfJ1xi0r1W/t6ipi/BOWtngHp1bNeGBbRcyVIOz6qaeKNP8Jj2pPqeixLW4c2o6s9HTjEZosZb439m/Gio9KY8LLDmxq9IanyjeZKh15uf6LBnxKXFZmpvFd5hFztD3pPkhjmw9VselUw760zYdGDZviiOdPCD0pZ9IIj488m2N88BUcmvatSpOfxVyXf2PXzz15ouFB0AVzOhPYW6VCc6o8geVtSuKUenNn3HHtkT4Axxf/hoUNXsGMsk+olPxTrnJTyuTTqxamlVEpPFWtNy1FSlyU8V3mEXO0Qamfm+lUw3De5jOHZ7H5OreKIqlRPMB9lLEPUiJI4dHJsznSb+xNA5tjask/8Rm85/zmIy05Dzv3VPqcEHod+34bgNmV/4xZlf+J/VO+RmpCrPEADR1Zuf37T+Dp8n9Y0uRVHJ3/K19volR+z4QBmF/nf1hY7znsU2m2uTQ+N2KOtqnbtvlQHySdSUOjhn3q8DafjYP0Np8wTrHlGqTwaOTZHCnFXdOxErfrLFMpNZ3Tmx+od5EKOHTt0X9Ut7uiv3PrFqiUuixmVXwC6z+rh+DDO/jvqb3nwuZlXA2fVfEvXK2k83/vh5ijLeuWcaqhSrGpik1FmhFdeRabzsXe2L8JAj10kUbWnQmPQp7NMeToHm7PGfM/ZY6tSvCB5vnh5LIpmPmBAya84oDtP3yKlNhI4x4KLjMRMHskZlb4B6aWcsDu0X35sHQTMdfPY6OKWicrY51f9zkEqaj1fog52rbo50cGqbf5GFXskd340g1t9KEiDZ9JQ20+0gcpPCT5NMdSD2+Oy3OZ4/cduV+SoOIKtfBQekSN41NKOmDDl41VROCJ8xsWs2gKZ20XR0x8w4H7HwPmjOIC0b0mZsQc7UDcB6lTbOqD5BSbIkjTqOGQljg6bwwvq5AijfAw5D2tPr6PRwSz0+oD909tb0OZ2LEF41RkqNPqnaO6a3NTpCXG695JlS5PL+OAqcocqWmcrj161lDi239hVqU/4ffi6j51u2N4Z4SePIDMezSEiznaiYxrkJRim65B0nQVtfnQkQubadRQRZC87kwMUsgneTbHiKCjfD1nyrsOWNzoNQT5zENaHg5BopQ5/tY17B3fXxnbnzG78j9xYMo3SE/Sb9aEkOvcp7aiTUlMf9+BxwapbWfsc0rPapEhU9Q4+R0dOfp0c+LIMjU+J/XOjZij/Yh/nkYEqavYug+S0mvvbtXVe6A1X4MMozYfuQYp5IM8myNVjakhe16t/6pI7t8qDe6K8KBA4957k5meigublqtUxxlzKj+hTPA9bsMwzVlHnDuGLUPbqmjxv3B3/DtWdqiAdZ/VM6vlLUuxwc51eQl7J/TnD4c5xBztTEaKnah+rroPUh/7ytt83Jz0sgoVQUofpJAf8myOdI3wwsYl/Gaj9HiRih6PLZqA1ASdHpsnC9GXTytzcuOpGg+nv2Pbtx0QHOBv3A+et17RphQmvPonLFe35zYs4v5Gczq+cALm134Gk17/M9Z9Xv+eLT1ijnaoXCn2baOGPfSoIR3aJWfSCPkhz+ZIkR41gu8Z1w+zKj3BVWXqLTu+ZCLCzxy+ayUZpby0KGLfxIFY1Pg1TH5LGWqDl3Fq5XR+E+vHxOD0qplcgaaUmaqMZIL3gopCtAqNqtYr25XB1d1+Zlfniznap3JGDcPYIM96zdGnGvasaRRpcm/zkT5I4f7k2RxNXPH3Ub+J62B25b9hWmkHLGlajGeeaQqGeiHpjUeR4enVM7F5cCt4uvybH+dZ47+c6tAKKiYri7/ePbo35tb8NxY2eJHPKybjuhe01GL3mL6YW+NfWNjwZZ6IMGemYo72Lbr+mBh5C1EXT2bvg6RlKd7dq3OKTVXscIkghQeQb3OkaI8Wz/p0r4kZ5fTKsnm1nsGyliWwqkM5pfIqqnufTdPD+V9cgfZwfArbhn2CW0d2Zf/GpkozNXfTIUrujk9i3Wd1cW3vxvuOflFqTz2OqzqUhXu1p/iNfvPQduPeHMQc7VwUQXIfJM1iH9UptlGk4Sr2V61km4/wQPJtjgQZ5KWtK7ivbGX78nw9cdKbDvj1WQfug6TqMlW157k+zY25+yYO5omXrIyc1Ds1PhZ7Jwxg8yRRNZve1PfqXSTo+6Mun8GmgS34v0drzU4smUSXNm9DzFGUnWIrRakU21TF9u3lqlJsR90oTim2ynakii2Y46HMUZOFqEuncHLFNOz4oTNf06H+x8VN3uTCyjqVxuwZ9yUvxjV3/ktqXAwOTvkGC+u/zaOBtOQ2L9DEA81dL27ytopWi6v//lQxR9E9lUTnYqvb7Co2bfPpXQfePWrqbT7uP3LPrKTYwp08gjlqaFsKTSiEHNvDKS41h988vJO3o8RcDVImaL4XMTMtjbf6XP1jE4KP+LNp5RVqK7q+fyuu79uI2Gvnjb/NQcxRZBL9vJPJINVtBPVB0iTN8K7KHF3gowyStvkcmTOKr5dLBCnk5pHN0RIRcxTlFqXYOacaUgQ5h5efUJGGOi70udh07KusOxNyEHMU2YcMg6SvKWMJ8vHka+bUA+nbi0YNySB/4WM8JMUWCDFHkd2If/YUQUaZtvl4qgjSjavYtOFen2qoj32VbT6CmKPIvpSdYuttPmfXzuZFJnrUsBo2DTZt8zlodsBAsB/EHEX2J6PNJzEiOGej+A+deFlu7lMNZdTQvhFzFNmlclLsMEScDdRtPiO78Cy2l5tzdqO4VLHtFzFHkf3KlGKrWyrS6Dafzrxb1Lubs97mQ9cgZZuPXSLmKLJvqfcDpdjaII9xFds/96jh4JZ6H+SpQ0hPlQjSnhBzFNm9cm/ziaI2Hy93+I90443ivM2HUmzeKH5AtvnYEWKOIpEhU4oddeEkziqDpCMX6Ewan54uulF87mgdQUqKbReIOYpEJnEEGa7eH6GICArMvgbJKXbPmtzmQ7PYZJASQdo+Yo4iUS7ljBoqg6RRw9Wz4M/nYtfG2i40akhHLlAESaOGYpC2jJijSHSXlEFG61FD6oPkFJvWnfGooauRYtMkjaTYtoyYo0hkRvQe0REkbfOhFJs2infVo4Y9XHjU8Ag1itO6M+mDtEnEHEWieyk7xQ7RfZBrZvFRH1SkoSq26dAubhSXCNLmEHMUie4no82Hvs4eNRzeidNr6oPMfaphmhikTSHmKBI9QPyeoTNponQVm65B+qv3FI8adnNW7zN9qiHvg5RtPjaDmKNIlBflSrG5D9KbrkGqFJtGDWkWmyJILtLQsgq5BmkLiDmKRHkVpdgUQapb06ghn2qoIkiqZGen2KcPSZuPDSDmKBLlQzmjhuH60C66BkltPj1rGqOGxsJcqWJbPWKOItFDiFJsiiT1Np/ZeptPHzrV0AWbBjZDoMdPRhU7wXhXCtaGmKNI9DBS7yNKsemW+iDPeukIklPsnq7KIJsjIPtUQ6liWyNijiLRQ8qUYlMUGUmTNCrFpjNp/HrVNk41bIEAOhf7+D7pg7RCxBxFokeSrmLTkQtRF0/woV00SaO3+dTEhv5NeFkFtfmIQVoXYo4i0SOK3k9cxY6kUw2PGqcadoNPdxcWbfOha5ByqqF1IeYoEj0GZW/ziTJONfTyUO87lWIbo4a8UXzeaISdkAjSWhBzFIkelwyDpFsySFMfpG/PWnrUcFBzHKEqNqXYSVLFtnTEHEWixyh+f/GoYRgigvS6M9oHSdt8vLtVx+YhrbRBntiHDJmksWjEHEWixy1Tiq3eazRJw1VsFUGu61MXXm4qxeZTDWWbj6Uj5igSFYRMbT7qaz60i1Ls4V34PBoaNSSDPOLxo56kEYO0SMQcRaICEr3XTKcacgTJ23zc9Dafrk6cYnMVm7f5yCy2pSHmKBIVqCjFDuX3XdRFOtXQwxg1rMvXIPnIBapi8zYfiSAtCTFHkaigRSk290Hm2uYzUu+D5Cr2kJb6yAU61VCWVVgMYo4iUSHotm0+54/rIo0ySN9etbC2q6MySKOKfXwvMiSCtAjEHEWiQhT3QapUWxvkbOz8IWebz8b+TRHgPgphJ/YjTbb5FDlijiJRYUq9/5Kjwvl9GBF0RBmk6VRDF5Vm18TGXNt8JMUuWsQcRaJCVvaoIc9iG1Xskd24SMPbfAY209t8eN2ZGGRRIeYoEhWFDIOkr3nUkLb5jOwKv961eR8kb/MxllVIFbtoEHMUiYpI/F6kCDLK2Obj4wn/H7tzeu3dXY8aSh9k0SHmKBIVpUwpNm3zoT5Ibw8VQbphXV/TqGFzPpMm9KSMGhY2Yo4iUVHLaPOhW65iG43idGhX9jYf0zVIMchCQ8xRJLIA8fvStM3nbCDOrJmdfSaNF52Lnb3NR4o0hYWYo0hkKTKl2Oo9mt0orgzST6XY3t2c9aghbfPhFFv6IAsaMUeRyJKUO8U+d/eo4ebBpm0+kmIXNGKOIpGFKWfUMEyvO/P24G0+1OLDRy581TJXii1V7IJCzFEkslDpFPsWoi+dNE41VCl2n7oqiqyBjQObcRVb+iALDjFHkchSZUSQpkmaIF9Ksd34yAWKIjfTNh/ug6RTDSWCfNyIOYpEFqycUw3DEHnhOM6snaMjyF61VYrtyKcaHvGQIxcKAjFHkcjipQwyOqdIwwY5XBkkjxrWxEYaNTT1QSbFG58C4VERcxSJrED0vtUpNm3zCeRlFZxi93DhNHvToBYImD0SIcf3SR/kY0LMUSSyEnGKzRvFQ40+SF3FplHDtV0cuUijq9hikI8DMUeRyJpkXIPkFJu2+fjM5QiSNorzqCFVsT30kQtyDfLREHMUiaxM/B6mCFLJdCbNrlHdOMWmQ7u2GKOGss3n0RBzFImsURxBhqr3ciiiLpw0NorrPkgvNyc9ajj3Fz1JkySjhg+DmKNIZK1SBqmPXFApdtBR3uazYzgtqzBt89GjhjKL/XCIOYpEVix6P3MVWykiyGjzoVMNe9bUo4bcKP6jrmLLNch8IeYoEtmAsos050+oCNJoFKdtPt2rc5EmexZbIsg8I+YoEtmCTBEkGyQVaebyudg0h80pNm/z0aOG0uaTN8QcRSIbERmj3uYTjqgLxxHkZWzz6V0bXl0c9cJc2gcpC3PzhJjjPXUTiWH3kNnHi0SWIZ7FjgjmM2l4HyRXsWvDp2fNnBT75AGkSYp9X8QczYoM8EEy930iUdHLFEFSm08EV7HdeaO4T3cXZZAuetRwzigVQUof5P0Qc8ylhNAb/Bs3PS4USIkAMiLVs0UrxWhlRQFpEchMCEVypHq8RJEiCxWPGhoGqZdV0Jk0XVUEWQdrO1fFxoHN9SQNNYpLim0WMcfsN1MwUqOUYsORHBOL+OgkxEWnIiY6E9HRWeo2C7HR6YiPSUZSTBxS4iKQGq3egOr77nwukcgiRAZJ23zU1xHnj3EEuUMZpG+v2jxuyKOGntYxapieDsTFqVBFxSoxKk65n+hxScrvMzKMb35IxBxJKgJMUUaHjGikJSUj6Ew6NmzIxFxPYNIkYMyvwPgJwKxZwJo1WTgSkI642BT1+FikxYTKdUiRxYre6xxBRlGKHYgzVKShWWze5lMdm79qpSJIY9TQgo9cuHABmDEDGD5cfR7H3K1f1Wd07Fhg3Dhg2jT6nALHjwPxj7DBzc7NUZmaMrb0uFtIT4xGaEgqdu0Cpk4FPvscaNYMqF4DqFwZqFYNaNAAcHPTP4x1G4Crl9ORmhDHabgu1tz95hSJilzZKbY+1ZAaxf1VBLmubx14uVXLOdWQG8Uts0izfz/Qvj1QqRLg4gI4OurPpUlVqgBVq+rPad26QNeu+nO6ZQsQGvpwUaTdm2OySqUzkqJx62Y6lq8AvvwSaNsWaN4caNFC35JJNlO3pq9bttImOWs2cOliBtISY5ESpd6Ad74pRSJLkVGkoa85xfb24Co2HbdArT4bBzTF4dkj9bozCzTIAweATz/VpkhBStOmxufyPqLH9O8P+PkB4eHGE+UDuzXHhLAbSI0OBtKjEBqcihXKGPt+BtSrp1/UwYMBT5VW+/iqKHE94Kte4Llzga++UverF75WLaBTZ8DdQ0eQSI9Beqx+3rvemCKRBYjf+5xi06jhUWPU0A0+yiDXdlURpHHsK0WQGcmWVaQ5dAjo0kVHiBSYzJ+vPpfrckQGaBJ9TocMAZo0ARo1Ar79Vn9/frFbc0xSUWNaXBhSUpKxyx/4XKXR9esDHTvq6xY7/TMRHqpMLytVPaNWeFgadu7MxPjx+nEfqvCdfmBknkmJqUiPj1DPL9cfRZYsI8VWkSQvzDU2ivOoYTdnnWIbo4ZpFrTNh8ytswpGypUDBg0Cbtww7jADFW381WeaAhkKYlqpTG/tWuPOfGCH5qjeHOp+ivKSY2NUWpyOmTOBNm10xDhhAnD2TBYSE5ORlhCFrMQwIDEUWclhSE+IRGJCkro/kx9nCu2pWHPqRAYSo2P5+qOuYItJiixUlGLTPkjDIIN89aghFWlo1HDz4OY5Z9JYSBU7tzlSVheskr77QQZJxdTq1XUaTplhfrE7c+Q3hro/Kzkc8VGJ2LE9E4PUi03XFwcMUBHjjkzjoPQobtVJVGlyQuh1TpdTKA1Xf0/30/cNHAg0V99H6bivTyaiwlUqkkrRo3oDSgVbZMEyNYpnjxp6u/PCXN9ervpUQ+PY15ATKsW2gD7I3OZIKXOYilnuB1W3R44EXF2BTz4BNm407sgHdmuOyIhSZpaKBQuz0K6dLsLQ9cOb19OQGh+NtFhljHe9qSgVD1H3x+D6tTS+ttGuPdCyJbX5ZCH0VhqQGS3mKLIamVJsPWo41xg1rMMLK3jUkPogTx5AelLRRpCma44VK+pLYHv2AFev3q0rV4B9+3TbT8+eumo9ZQpw5ozxRPnATs3xlnpUDMJCMzklrlkT+Ogj/dslPT0FGfHhSAo3V1i5ydcq0+NUip2Wgm3b9W8lCt1/+kkZ681M9byxMj0jsh4ZESRvFDdt8xnlxica0k5IPhdbpdhskEXYB0nmSEZHnzW6BPbFFzqCvFOUcvfpo2sCZI7TpwOnTilPeIjg147NMRYhoVkYOUr3TpE5Uo8jkMLjgTRKaO7NRH+frqJHIBkHD+ofAv02G/YtcP06fX+cmKPIqsTX4TnFDlMptt4HSbPYdC62V5eqbJDcB0mz2EWUYpM5UpWaCizUUUJV6/Ll79YHH+hb6oXs3VtXr1OpnvoQ2J85hueYY6gyxxEjtbm1JXPcTd+df3OsUAH4ZpiYo8iapQySRw31PkiuYg/vzAZJ1yFzUuyDRdIHaTJHMj3qN/74Y933aE50mYyiyx49dDvetWtAJiV1+cSuI0cyR1PkSObon8/Icf8BiRxFtqOcPsgQHjXkbT7UB0mjhj1q6H2Q1OZDkzSFHEGarjnSNAylyz4+ujHcnOjy2MSJ+nE01LF8uemzmT/s+ppjeFgGxo3X1xzJHKlfMVXF4On3vOao3kBclAlHakoKjybRNUeXGsAvv8g1R5ENyEix6TPEfZA0ajiStvnU5TNpqA/yiDsZ5N5CbfMhc8xdrQ6h+OQe0KjgsWMqm/tGt/HQ9ck//jDuzAd2ao5GtToiBQsW6Gp1axWGT58BXL6UjrSEGGTEq9+ipn5FNrqb/Gf6e7r/ysU0Hh+ka5UUwru7ZyEsJFXF71H6+8QcRdYq+owog0xU72NadxbEo4a0zYdGDfU2nyPutA+y8BrFTeZI1xOpCZxS5fuRqHybqtQ1VOBCvcjSBG5wP3M0NYFTn2NcdAK2b8vg30TU59i7D7B+fRaSE+kKbgxSY2gGW/c50i31PdJ+x7TkFGzakInPPtPXP/r1A2/xiY5IRFaK0edIpmrujScSWYE4xaZG8SjaB3mUN4pzH6RKsb1okmZwSxyePQIhx/YUSgSZ2xypv/jSJeOOe5CVBcxWwYuTE1CnDrB0qXFHPrBbc0yLUb8dY1UEeDkdc+boESOqgo0Yoa9bREamqAgxFkiPVIrg2/TEGERFJ+NIQBa37lDITr+VJv8OnD+XgaQYPV8t5iiyCeVKsaOpD1JFkP4j6VTDD+Hl5oQNA5pkz2KnJT3CbrA8kDutpnadWxSn3IO0NCAoSLfX0SUz+ozSCrP8YofmqMxL3U/mRbPVaWlJfD2CLtzSbDWlyMOGqTDcK0ul2BlITU5HRlo6UlPSce1qBvz8svDDcN00TmZKF33p2mNqcrJxrVJMUWRDohQ716jhORo1VBEknUfDKTZfg6RRw4Ld5nNn5Hjxoq5A3yn1McSJE3r3Kj2+YUOgb19gxw7jifKB3ZojFUxSooLVr5lIRISmwNtbd95THxWZJPVI0YIJz7nA/AV608eE38CpNL3g9BuphzLGZcuA4OsqDU+N4mhUCjEiWxMZox41DEMUzWJTo/iPplHDasaoobHNp4AaxckcqQmcVpZ16qTnpufNu1uUBf74o+4iMQ13UHp9+bLxRPnAjiNH+sHf5MpyZlIUIkNTsXZNFl/spQo0heJkkmSWNJ9paj6lZRMdPlaRZj9gydIs3LyhIsukaH4e2ecosmXR9Uf6/ERdPMXXIE1VbG9j1JCPXKBJmgKIIGnZLfU2UvN37do5n8s7Zfqc0ueXCq3URRIY+HCN4HZujkoq0ktVER9t4IkMS8GBg1R51hUx+q1DW4Wp8ZRuKeWm5RQUsu/dC65O05x1aqxO03O/kUQim5MRQfKhXZxiz9N9kDRqqKJI06ghHfv6uPsgaeCCIkZnZ21+ZIIUGeYWmSN9TumSFxVZaecjtfRQ5fphEHNU4hSbKtHpUUhNSsLF82nw35nJF3EXLNSpNd2uXq239pwPSkNKgvrhp0cbFW0xRpF9KGfUkLb50KghNYqrCLJXLXh1ccQmlWLrUcP9j3XUkJq4ae0YLZSgqRdzoktfZIj0Od29m/qO9XXIh0XMMZcoNU6JCeNoMC0pUf32S0FGWgbSlfg2JZX/Pk3dT4+jx5t7HpHI1pUUFa4+S8EqgiSD1Ecu+PWpzVvFuQ+SJmlUBPm4qtjUmnNn8eV+osc/KmKOuUQRJP3A01SajKQw0G5GPrvaJPqz+nsaH0wiY5Tii8hORZ8jU4pNRy7oNh/TqKELNg1qgYA5I3mSxtKOXMgrYo7mRKanRAtu75TpPrPfJxLZkUwptukapB41dOMizdrOVbGRJ2moir0X6RZ05EJesUlzTI4KxYUNi7BtaFt4da6CXT+54cr2VYi7eSlv5pgtMsE7Ze5xIpGdyjDI7G0+3p58Jo1vr1qsTQObIoBGDY/vtzqDtElzTI0Jx+VNS+E/rB383Kpi7y/dcd1/DeKDL+fTHEUi0YPEnymKIHnU0LQwtzun197dqus+yDlGBJlStBvF84NNmmNKVAgCVs7Akj4fYnrz4lg1uBVO+M1HUsgVdWc8MhPoKANzxyCIRKKHUq4UO5r6IFUEySl237rwcquWvayCZrGzUnMaxdPT0xAeHoKrVy/g8uUg3Lp1HSkWcGYNYVPmmJmZgfj4GATs2Y7pPwzAF/U+QMfyL2FgM2fM+/U7HN2zFdE3LyMlOpQ384hBikSPUerzxEUaFUlSmw+fajiqK1ewKcXeOKApX4MMP0ULc+MRGRWB/Qf2YfHiRZg4cRLGjRsPT08P7N7tj5CQYDbOosRmzDElJQU7dmzFDz8MRfs2zVDHqRaqlHRF+WK14Vi6DhrWqoeO7Vpg3M/fIXDfTqQoc0xX6Tfdmv1Bi0SifCv3qCFdgzxHkzQ/docfrTvr5oSd37bH9snD4D5+BAYM/BztO3yMhg0/Ra1aveDq2kd97Yb27Tvi8897KdOcj9DQ+2yYKGBswhxjY6Owbt0adOrUA2+8URNPP11X3fZGqVLj8X5Zd3U7Fm++1QtPP1MbZUrXxtcDB2D/jnWID73GBikRpEj0eMWjhirw4G0+tO5MGeSmfo0wv5Mj+tUuiSol3sfzL7jgxZda4623BqvP6BSUKTMTJUuOxKuvfoLnnnNB7dqtMXPmdFy7dtH4pBcuVm+OyclJ2LDBB82aNVYv6ofqRZ6GKlX3oabredT58Bbq1otEnbrBcHE9h4qVtqsfxHco/nZ19OvrhoA/toN6G1ONrSPmfsgikSj/otSapmjYIOlcbJVi+wzriN7VXsE7z/wPL7/QFuXKLke1aoEqYryoIsdgZYYhSlfg7HwCZcuuwWuvuaFKlVqYOvU3FUHeZ/V3AWH15vjHHzvRuXNP9UI2VNHiWNSte4t3M5LoPGlaYku3LdWf6WtHx0C8/PIglC5VD98MHoQTh/5QDhuH1NiI7IqbSCR6REWGsjmmxNI+1CTcOn0YY/t1RvnX3sbzz7dGmXJeaNwoJfuzSp9Nkulz27hxOkqX9sJLL1HK3Qpz585RGWK08akvHKzaHFNTUzBmzEi8+aYz3n13EurVu8Vbc2g7N23lINGfTV/T3zdpkgkXl9N4+ZU+qFC+GhZ7TOFtOnTtMft4A5FI9FhEn6mMlDicDtiD9m2a4/nn6qFiRV80bBif/Zk0fU5zf1ZJDRsmonLlLXjhhSZo27Y1jh8/gkyaDSwkrNYcMzLSERR0Br17d1cvXh1UqLCFf+PQi216oe8UveAt1GPIIN8pPgnvvFUNwwd/hlO7NiD8zGFEnw/kW5FI9OiKPBuAyKAjCD65H2vmT0etGjXx4svdVSR4Ha3U5zC3Kd4puo+iyDp1bqlMrzdq1qyPtWtXISam8KJHqzXHuLho+Pp6o02bLnjrrV5wdj7JL+b9XnBScxW6k4FWqOSH90q0xaeN6mPRiD44MvcXnF4yAUfn/yoSiR6DTi4ci5OLxmLL5K/xfbe2qFTGFcVLjEb9BvEcyJj7fOYWPaZBg0SULDlRfb474LffJuLSpXOGAxQ8VmuOISE3MHv2TNSv3wPvvfeLSpUv8jWLB5qjEcZXdTqAUiW+wIely2Jk4/fg3ac2tvZviHWf1xOJRI9Bm76sz5revgI+rlIS77/VGGXLLUKDhkn8WTX3+cwtekyDBkkoW3YZqlb9DN98MxzHjh00HKDgsVpzDA6+imnTpqBu3V4oVWqCCrsv58scqzkHoHSJgXAtXhrDXF/Dqk6VsaFHdV77LhKJHl1+3ZyVnDCx6Tto9f4bKFOsOcpXWImGjZLzZY7ly69GlSr9MGTIdzhyZK/hAAWP1ZpjVFQYli5dpF5ENxQv/hVq1AjiMDwv5kiqXGW7ihy7orWLK2Z82RZ7Jg5E4PRh2D/5K5FI9Bh0eOrXrLXD3fBlq3r4oGQ9vFd6GkeOeU2rGzZMRunSc1CtWlf8+ONonD173HCAgsdqzTE1NRn79+9Fly5d8eqrrdRvln15MkfTb6zSpeehZIl6GPJZT+xdtwwhx/ci6mwAbzAWiUSProjTB5UO4cK+LfCcNBrOVV3x2mv9VbYXnmdzrFcvGsWKDYOLSzPMmzcXoaHBhgMUPFZrjllZWSp6jMTQof3x3HOOyuwWK2NMy06bzb3YpqixXr1IvPLK13i3RCXMmTkJMZFhyFBmm5Wepm5TRCLRY1BmGikVqYnxCDy0F40bNcT//tcUzs4B2Z9Fc59V+jvT/dWrn8Azz7RRn9l62L17B7fvFRZWa44mli9fhJo1W6jfLr3xwQcb+RoFRYcm0Quc+8+1at1CqVLz8dZbbfHxx51w4MAfxjMJglBQxMRGq7R4FMqUaYR33hkBR8cjbIQUHZJMZkifUVMGWK3aCZQoMUZ9Xpvg22+/xs2b14xnKxys3hxv3ryOKVOmoHLlOnjxxc6oWnUX6tdP4F7GJk2ylKivMQuNG2fiww/D1A9nkUrDm6NNm4/h5+eL+PhY45kEQSgostT/jh07ikGDBuHtt13xxhvfqVT5LBo1SlMmafqcUuSYpf4uHa6u51UA8zOKF6+H/v0HISDgEDIyCndLj9WbI3H58jmMH/8TnJyaKYNsh5deGoJ3352OcuW8UbHiVpQvvxYlS07DCy98iTffbIW2bT/FmjVLEBcXYzyDUFjQslM6eOnCxqU4tnA8Ds/8AQenfYsA9x9xatUMXPvDD/G3rhiPNk/YqUMImD0Seyd8y997pw5N/w6HZnyPw7OGq//GBFzathoxV84iMyPdeAahKMjIyMD+/f7o1+8LjgaffbYzXn99JF//L19+Aw9ylCu3TJnnr+qz2l39fXN8+eWX2LdvJ39vYWMT5kjcuHEd06ZNRb16DfH++44oW7a5eqH7qlR7iFJv9cI3Vz8AJ3Ts2Anr1vkiIeHxnIom5I0sZUwJoTdwccty+P/UA6s6fAAPp79jWikH/F7CATPKO2BRg5ex/vP6CJw3hg+HT0swH9WfXj1Tfe8/MLmYA6a/74Ap7+rnMGlKSa1ppR3gWf1f8OpaHQenfofgwzvUc8Y9nqPphIeCTO7o0UAMGzZMpdY11OfURamD+qz2V5/Pwepz6qY+r/VUBuiCr74aiiNHDvM0XFFgM+ZIUCXrjz92YMECD4wa9RM+/3woevQYqH5TfY0xY37FsmULERh4UEWMkkoXNlHnT6iobhhWf1IRc12fxswPHDBVGdjktx0w6S1lasWV0ZVxgLvjU1jU6HVsGtgcF7etAhXK7uTUimmYVdEB41/SZjhZfT89h0n0Z5Z67qnvOWBWhb9gXu1XsPWbdri2Z8M9TVcoHGiJ7eXLF7Bxoy9mzpyqjHI4evcejJ49B3Ev4++/T4Kf3xpcuHAWaWmpxncVPjZljiYSExMQFHQKe/bswLZt61VY7q9e6CD1QhdepUvIIfLCCe57W9ToNY7y3Kv9HV5dnLBjRFeVGvdXGoBdv/TGus/qY37d5zFZGSWZ57ovG+DyzrVIT7793JEza2Zz1DnxdQcsbf42dqlIlJ4jR/Sc/fHH2C+waXBLLG5cjCNUD+f/8GMjggKNZxKKmoiIMBw7FgB//83YsWMjDh/eh+Dg68a9RYtNmqOJrKxMpQy+FYoAlb6mxEUj0PMXLGzwKmZWcMDC+i9ix/DOuLh5OeJDriNTRRGklJhI3DiwBXt/G4BlrUqoaO9PmFnxT9j8VWtEnA1UaXnONScyxzlV/4pxzzvw6v344CvZz5NbacpUw04f4muPS5q8id/f0WZ6aesq45kEyyAr+7NKX1sKNm2OQtFCR3HePLwdG75spK//ufwHe8f350PgU5Vp3kl6ShKir5zB0QVjlYm9w2nx0mZv4eSKqXy90oQ2x79g3HMOfDb5nZHlnUScOwa/PnUw7kWKHv/Bp+MJwoMQcxQKjPjgqypq/BlLmr6O2VX+jg39GuPWkV3Gvfcm5uo5+P/cCx7Vn4ZnjX9i67cdcCtwt3FvjjmOJXMc2hYZDzitjqrb3m7V8durDirFfl1FjiuNewTh3og5CgVG2MmD2Pp1W8yp/FcsURHgiWWTeUP0g0hLjOdijJcytFkqFV/Z7n2cW7/IuNdkjk9i3AsOHJVGXzqt0veou0QbqYMP78T+iYNUWv0G5rk+yyk9VcIF4UGIOQoFBlWGV35UGpPedMDazlX1mcV52ORMo6EJIdewc0Rnrmi7V/snp9omuCCj0uOJb6hIsNFrKrVuje3ff3qXtn33MXx7fqhS9LewvNW72PVTd9w4sFWl9FHGMwnCvRFzFAoMKnzMr/scp7++PV0Rcy3vi0qpoLJvQv/sdpyDM7437tHm6Onyb0wpoXsZf3vNARNeNqNXHDD+Rf2YNZ2q4Ny6Bfy8gpAXxByFAuPi5hWY6/o//PqMMsdetRB7Pe9HbFKEuW/iQO5XpPYfmnwxweZY4/+4+kwVcGogv5fIGGdVcuCm85PLfuequCDkBTFHocC4uGUF5t1mjheMex6MyRypqVub4zDjHm2O7k5/5wLLyo/K8AgijSKa094Jg+CjotalTYthY//G3EKUl+uegiDmKBQYl/29uBBCKa63mzPCzx4x7nkwKTER2P1LL56AmVnhrzji8ZNxj6kgo/scNw9uiZTocOOeu0kMv4nTq2ZhecsSmFPlH9gypDVCjhXeNmnBehFzFAqM4ICdHLVRaruibWmc37hEzzY/ANoFGBzgz5Xo6eUcsLhJMTZEE9nmSK08yuzS4u+/QCT60hn49q7D1yapgHNxi7TyCA9GzFEoMKjFhkb45tX6Hzxr/JfbaCLOHTXuvTdJESG8VWdh/dfhXu1JNsnrezca994eOdIMNp2PfD9S42OxWZkoFYbmOP4VZ709jHsE4d6IOQoFRnJ0BM5vWMJtPBQ9LmzwCo7OHa1S3WCzCyWyMjM4nabrgmvU99BmHdrUEzB7FGKv5lS6c0eOm4e0MjttY4Kq07Syn6rllN7Pc/0PV60F4UGIOQoFBq0piwu+gt2j+2J2pb9ghkqRqe/x4NRveKzwtrG/rCxEnj+OE4t/4+LNHMen2BzJ1G4e2oGMlBwzvd0cW6vI0HxaTfO6Icf3Ye/EgcqYX2aDXtWhHK74exuPEIR7I+YoFDjX923i9JcMj9pv5td+lk3tiOfPbHSk48oUac/j8pbvcl/jdDaysji5fOpd7Tf0ePdqT3G1elWH8ji2YGz28+QWPef27zuq9PxVrnjPq/Vv3tYTdfGk8UyCcG/EHIUCh1Lbq7v9sKF/E8x1+T/MrvIka46jIRUF6lv6+78q4/sHVrUvq6LIiXz98U5Or5rB30MFlpnlHTCnyl/0c+SW8byz1X20z3FOlX9hw4AmbNS0jVwQHoSYo1AopCXG8SZuKrRQ2kzN4bTgljblUGFl0hvK5JSZUbM2peEXNy9DQoj5vX4nl09hU+TvK5bzHLfpBQf89jotulXRZbvy6jm/UAbte88UXBDuRMxRKFTiQ65xc/jhmcOxY0QXbBrcilPubd9+jP2TBuPM2jm6on2fowxu7NuMrcM6wK9PC2wapKS+/y4Naomt37THnrFf8LEKdD1TRgeF/CDmKBQ6VIhJiY1CUmQIV66pFScx4haSYyJ4Iw9Vre8HfX9i+C0khKrvo+81J3pees7oMI5aH/ScgnAnYo6CIAhmEHMUBEEwg5ijIAiCGcQcBUEQzCDmKAiCYAYxR0EQBDOIOQqCIJhBzFEQBMEMYo6CIAhmEHMUBEEwg5ijIAiCGcQcBUEQzCDmKAiCYAYxR0EQBDOIOQqCIJhBzFEQBOEugP8HXoyJrKYu0tYAAAAASUVORK5CYII=[/img][br]Pelo teorema de pitágoras, tem-se que a hipotenusa deste triângulo é dada por:[br][br]AB² = OA² + OB² [br][br]Se OA = OB =1 então, podemos reescrever a equação,[br][br]AB² = 2.OA² [math]\longrightarrow[/math] AB² = 2 [math]\longrightarrow[/math] AB = [math]\sqrt{2}[/math][br][br]Como vimos, existe um segmento AB que, segundo o teorema de Pitágoras, deve corresponder a um número cujo quadrado é 2, o famoso raiz de 2. [br][br]Será que poderiamos obter uma expressão decimal através da reta numérica para este número? [br][br]Tente buscar uma expressão fracionária para a raiz de 2 com o auxílio da construção abaixo.[br][br]Perceba na construção a representação da raiz de 2 na reta numérica. Escolhendo valores para n, é possível subdividir um pedaço da reta numérica em múltiplos de uma fração da unidade.

Por exemplo, fazendo n = 2 vemos que a raiz de 2 está entre 1 e 2. Para n = 3 a raiz está entre 4/3 e 5/3. Para n = 10 vemos que raiz de 2 é um pouco maior do que 14/10 e menor que 15/10. Para n = 12, vemos que raiz de 2 está bem próximo de 17/12, só um pouco menor.

Se raiz de 2 não coincidir com 24/17 tente outros valores para n. Veja, por exemplo n = 58. Faça o seguinte, escolha valores grandes para n, bem grandes. Veja o que acontece com o segmento representado por 2. O segmento fica preenchido por pontos, não? Então, a raiz de 2 vai coincidir com um destes pontos, não? Para tirar a dúvida, use o recurso de ampliação. Ah, lembre-se que você sempre pode escolher valores cada vez maiores para n.

Você concorda que é difícil perceber se a raiz de 2 pode ser representada por um número racional ou não? O que sua intuição diz, parece que podemos encontrar um valor para n, suficientemente grande, que finalmente fornecerá uma representação fracionária para a raiz de 2? Ou estamos diante de um novo tipo de número?

Esta atividade tem o objetivo de compreender como se encontra e determinam alguns números irracionais na reta numérica.

Para começar, vamos relembrar o exemplo do triângulo pitagórico que vimos anteriormente.[br]A partir da construção abaixo você irá perceber a essência do conceito de irracional e como determinar sua localização geométrica na reta numérica.[br]Inicie a atividade e siga os 3 passos, observe como é realizado o pensamento algébrico.

Nesta atividade você pode ver como determinar outros irracionais a partir dessa construção geométrica.[br]Para isso, siga os passo a seguir:[br]1° - Clique em Iniciar[br]2° - Inserir[br]3° - Digite um número de 1 a 5 (enter)[br]4° - 1° passo[br]5° - 2° passo[br]*Dica comece pelo número 1.

Essa animação ajuda a perceber como as raízes quadradas de números naturais se distribuem pela reta numérica. Note que a figura representa o gráfico da função [i]f[/i]([i]x[/i]) = [i]x[/i][sup]2[/sup]. E vale lembrar da propriedade: A raiz quadrada de um número natural é um número natural ou é um número irracional.[br][br]Através do controle deslizante, aumente o número de raízes da função quadrática, perceba o que ocorre.

Você provavelmente conhece o termo folha de papel A4! Esse é o tipo de folha que você mais deve encontrar, em documentos ou em textos escolares.[br][br]Você sabe o que define uma folha de papel A4? O que suas medidas têm de especial?[br][br]Pois bem, essa história é bastante interessante. O visitante tem aqui a oportunidade de poder explorar sobre o assunto. Mas, agora você precisa tomar uma decisão. Você pode seguir dois caminhos, pode seguir o caminho tradicional, que é ficar sentado assistindo a um bom vídeo sobre o assunto. Ou pode tentar participar ativamente dessa história, explorando e descobrindo diversas informações curiosas.[br][br]Se você quiser só assistir ao vídeo, siga em frente. Se quiser ter o prazer de descobrir o que a folha de papel A4 tem para nos contar, pule o vídeo e interaja com as informações que o seguem. Você decide. Se optar pelo segundo caminho, pode voltar tudo e ver o vídeo. Se optar pelo primeiro caminho, perderá a oportunidade de realizar descobertas. Agora é com você, visitante.

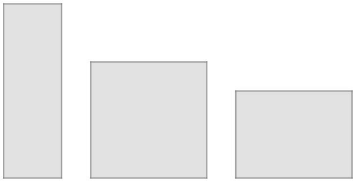
A ideia do papel A4 é você ter uma folha onde possa fazer um desenho e, caso queira fazer uma versão em escala menor, baste você dobrar a folha ao meio. Você sabia disso?[br][br]Para deixar a ideia mais clara, veja as três figuras a seguir. Você acha que elas servem para fazer um mesmo desenho, mas de tamanhos diferentes?

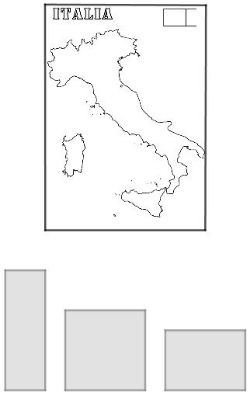
Vamos ilustrar melhor essa questão. Digamos que você esteja em sala de aula e precise fazer a reprodução de um mapa, só que menor. Digamos que seja o mapa da Itália. Pelo menos eu gostava de tentar desenhar o mapa desse país, o difícil era me controlar para não completar o desenho com uma bola.[br][br]Você acha que as três formas são igualmente adequadas para fazer esse exercício de reprodução?

Veja mais uma imagem que ilustra como podemos trabalhar a mesma figura reproduzida em tamanhos diferentes. Aqui a reprodução é feita com um pantógrafo. Repare na variação de tamanho das folhas para os diferentes desenhos.

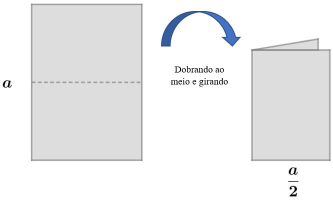
Voltando a questão inicial colocada aqui, a ideia da folha A4 é que se você quiser fazer um desenho com metade do tamanho da figura original, basta dobrar a folha ao meio virá-la. Você deve conseguir uma folha de mesmo formato que a original, só que com metade do tamanho.[br][br]Veja a figura a seguir.

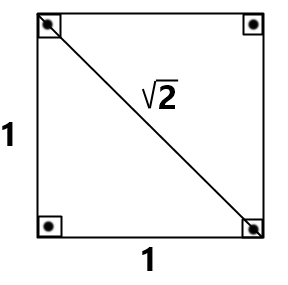
O leitor não gostaria de tentar? Pegue uma folha qualquer dobre-a ao meio. Será que você vai obter uma versão menor da folha original? Será que isso acontece com folhas de proporções diversas? Ou precisamos desta tal folha A4? Só com ela isso é possível?[br][br]Você pode fazer a experiência com diferentes formatos de folhas. Tente![br][br]A animação a seguir permite explorar bem essa questão. Você pode dobrar uma folha ao meio e comparar se a folha dobrada possui as mesmas proporções da folha original. Pode fazer isso para diversos formatos. Explore bem os diferentes casos![br][br][color=#ff0000][b]Lembre-se![/b][/color] [b]Você pode:[/b][br][list][*]Dobrar a folha.[/*][*]Girar a folha.[/*][*]Aumentar a altura da folha ([color=#38761d][b]a base dessa folha sempre mede 1[/b][/color]).[/*][*]Usar uma imagem para ajudar a perceber se as 2 figuras são proporcionais.[/*][/list]

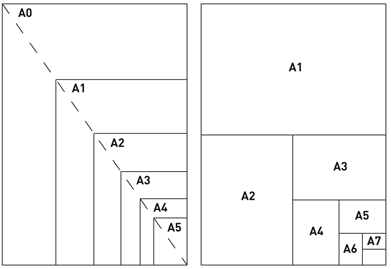
Vamos conhecer um pouco mais sobre a folha A4. Na verdade, existe uma série de folhas definidas pela propriedade que estamos estudando aqui, ela segue o padrão internacional, ISO 2016. As duas figuras a seguir ilustram algumas dessas folhas, começando pela folha A0. Dobrando-a ao meio, obtemos a folha A1. Dobrando esta última, obtemos a folha A2. E assim sucessivamente. Provavelmente o leitor já trabalhou com as folhas A3, A4 e A5. Pode verificar.

Na verdade, as medidas da série A são bastante conhecidas. Podemos até mudar o trabalho feito na animação anterior. Em vez de trabalhar com as formas, vamos brincar um pouco com as medidas das folhas da série A, A0, A1, A2, A3, A4, A5, A6, A7.[br][br]A construção interativa a seguir apresenta uma tabela com as dimensões de algumas folhas da série A, todas as medidas na unidade milímetro, e permite avaliar a variação de dimensão entre as diferentes folhas. Você pode verificar a covariação entre alturas e entre larguras ou entre altura e largura. Você pode verificar que existe uma proporcionalidade nessas variações. Explore os números fornecidos pela construção a seguir, verifique os valores com sua calculadora, e responda ao questionário que a segue.[br][br]ATENÇÃO: Estamos trabalhando com a unidade milímetro, assim, a casa decimal representa a unidade micrômetro. As contas apresentadas a seguir são arredondadas, mas com uma ordem de erro menor do que a de um micrômetro!