Berechnung von Rotationsvolumen
Rotation eines Funktionsgraphen - Rechtecknäherung
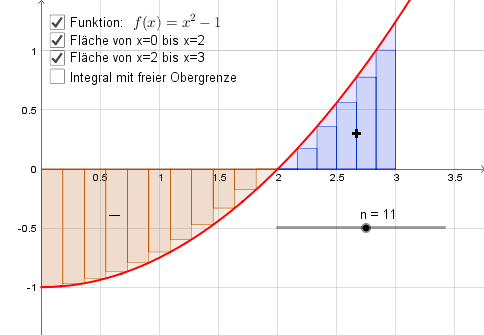
Und einmal mehr: die Rieman Streifen. Unten sehen Sie ein Bild unserer aus der Einführunf in die Integraechnung wohlbekannten Funktion. Die Fläche unter der Kurve ust durch Rechteckflächen angenähert.[br][br]Stellen Sie sich nun vor dieser Funktionsgrapph würde um die x-Achse rotieren:[br][br]a) Wie würden Sie den entstehenden Körper beschreiben? [br]b) Welche Art Körper entsteht aus den Rechteckflächen?[br]c) Geben Sie die Formel für die Grundfläche des aus den Rechteckflächen entstehenden Körpers an[br]d) Geben Sie die Formel für das Volumen des aus den Rechteckflächen entstehenden Körpers an

Der letzte kleine Schritt zur Volumenberenchnung
An Stelle der Streifen werden nun also Zylinderscheiben aufsummiert, d. h. integriert. Man sieht hier nochmals schön, dass es sich bei der Bildung eines Integrals um eine Summenfunktion handelt (fern ab von "aufleiten" und ähnlichen Banalisierungen)[br][br]DFamit sind wir schon fast am Ziel: So wie bei einer Fläche die Rechtechstreifen f(x)dx aufsummiert wurden, weren jetzt die Zylinderscheiben [math]V_i=\pi\cdot\left(f\left(x\right)\right)^2\cdot\Delta x[/math] aufsummiert. Dann macht man noch den Grenzübergang [math]\Delta x\rightarrow0[/math] und die Summe geht in ein Integral über:[br][br] [img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAY8AAACjCAYAAAByg5IeAAAQwElEQVR4nO3dbbGrOgOGYSygIRbwgAQ0YAEHOMABCqoAAzWAAzzk/XHeh52yaJsA4aPc10xnzqyz99q0TXjId2IBAAiUHH0BAIDrITwAAMEIDwBAMMIDABCM8AAABCM8AADBCA8AQDDCAwAQjPAAAAQjPAAAwQgPAEAwwgMAEIzwAAAEIzwAAMEIDwBAMMIDs57Pp02SJPorz/Oj3yqABQgPvFWW5cuNvm3b1b9zGAZb1zXhAVwc4YG3hmGwWZaNN/o0TW3f95v87qIoCA/gwggPfDTtvsqybJPf+3g8CA/gwggPfNU0zUuA1HW9ye8lPIDrIjzgRd1MenVdt/p35nlOeAAXRXjAyzAM1hjzMv4xDMPRlwXgIIQHvHVd99L6KIri6EsCcBDCA0HcabZJktimaY6+JAAHIDwQLM/zl+6r5/N59CXdVtd1tixLm6apTZLEGmM2m9AAfEJ4INgwDOPNasvpuwinz7/vezsMwzixgUBHbIQHFtE6Db2qqjr6kqLSynh30sDj8Xj755/Ppy2KYvHn0jSNzfP866y26XVoXIrWB2IjPCKZ7uE0rczuyu2rVvaqql7ew6eb6dVlWWazLLPDMIwLJ9+ttq/r2qZpuno7l67rrDHGlmXp/XcU6rFbHiq/W+04gOshPCJxV2bPPX32fT92/YTcHM5mun3JL07f1SQBn7UtVVVtOg6kLWJ8yoimU8cuT33fM2EChEdMGlh+d9NJ0/Ty4wVuCP7qivE0Ta0x5uufU5fRFhtIuvQg8ulGHRIya1VVNT40XL38YjnCI6JP4aEbzRYrtY/Wtu3PTt/V9+SzpiXPc6+QWUIzquZadnsGh7V27JLT+A9dV/dEeESkLc3nAiLLsp9aZDfdvv0XZvu4s5e+jUn5tA7W0FjG3O93x2Nia9t2DDGNeZ3pYaEoip8oe1dAeET0rq9cFfCXntim27dvcTObm+H06bXlTWzamnJfc3Qj/dSS1AD43DiX/v6n2Vlz3YLqQnI/66Zpok3AyPN8vHYF5ruuyrXvd4mu61h7tBPCIyKFh3tT0xqJrSr3dMsQ31cM0+3b194YqqqyTdO8hIgrTVPv1pu7Mj6Euh7X/rm+722e5y9P7LrBua22TzPWFM7u73z3/fqUL12z7ziV/j03IDXeNX1Q2OL9LqXZbgRIXIRHRLphuRV57ib4S9zt27ccPM/z/CUoFJq+rY2l4eE7KKzZZj7ctRhN09g0Tb3GvnSz36rFGhoeVVX9KbsKgk+TBJa+3zWyLCNAIiM8ItKNVOEx9+T2i9RVsWWXxDQofLqJXEvCQzc9n/cRGpYKpZAb3LfZe6FCw2Nu6xONxXxrAS55v+7fXfr65Qe1oxEeEU1X+xZF8ZNTWV0aK9hyCufczLRpF04MCn+fqbeh4aEbd8iNdOvwCKGQmGv1vOu6ci15v2vQ8oiP8IjIDQ/999aD5Gcb80jTdPPJAGo1uLbuFpsTsk9UyPW4Z6OEfE5HhsenBx99Tu9Cdun7XYoxj30QHhG54ZFl2UuT//l8jhXq8XiMA4x73BRjUWtg60FQTUWVkO6kNYwx3uMYvqGsWWnfbrhzth7z8KXu1nfXqtbm3DqTNe93CWZb7YfwiEizj7RC2W3WF0UxVqyqqmye57bv+7EiXm1cRGMQWy9U043LDYqQ7qS1/65vkPvMyur7flzMNwxD8Oe1R1fdHD3Jv+uW0nuZBu3a97sE6zz2Q3hE9m1K4jRYFB5XWgOi/vAYC9XmZvMoPB6Ph+26LspiS30PvlOqPw3gu1Nq3c9I/fLDMNimaT6GoW6+R7RK1QLTmfNzL417qBW99v3i/AiPyD5VeLVM3EqkjfWuwt3bausnPnfdiBtKfd+/LD6LEbQKA98uuE9daQpXrXtwf64xom8h9WmFeUyhY2p1XW/yfnF+hMeB5loZxphLbVui7pozbVGxhSVbjhtjok0NLYriZ3ctxjURHgcqy/LlZqPm/lVuxJoFdaWw86EuotAgCF24GPp7eVrHmRAeB5q2Mtz1DG3bnrpPWNc6nQjwC9QiXBICMc7zuFprFPdAeBxET7fTfa80qHjmp0z3DPOrzQr7RjfrNYP/mp20tgWiaaearQScCeGBYL7blF+NBsk1jXoNzQKLfYY5cBTCA0E0TfaqCxkBbIPwgDd30SPdKMC9ER7w4u5PtNX2I2rF0DUDXA/hAS9a6b3lflL6nWwnAVwP4YGvYmyzbu1xezUBWI+ai49ibbPu7n8E4HqoufhIrYMtFyxqt1XCA7guai7e0rqHmK+tu8IA7IPwwCztjBr7xXoR4JoID8zSbrmEB4A5hAcAIBjhAQAIRnhgUzrjA8Bvo5ZjU3meM4MKuAHCAwAQjPDAJnSyIBsdAvdAeGAzWlTIdu3A7yM8sJmqqhjvAG6C8MBmsiyzZVkefRkAdkB4YBPDMGy+gSKA8yI8sAkNmHOwE3APhAc2ocWBwzDYsiw3PfsDwPkQHtiEDo0yxtB1BdwA4QEACEZ4AACCER4AgGCEBwAgGOEBAAhGeAAAghEeAIBghAcAIBjhAQAIRngAAIIRHgCAYIQHACAY4QEACEZ4AACCER4AgGCEBwAgGOEBAAhGeAAAghEeAIBghAcAIBjhAQAIRngEyvPcJklijTFHXwpwOUmS2CRJbFmWR18KViI8FsiyzBZFcfRlAJczDINNksQ2TXP0pWAlwmOBNE0p/MACz+fTJklin8/n0ZeClQiPQG7hr6rKpmlq0zSlMgAemqaxaZraYRhsURQ2SRKbZZkdhuHoS0MgwiNQ27Y2SRJbVZXtus4Ow2CNMXRjAR7KsrRZltmyLG3f9+PDGC356yE8ApVl+afZnee5zfP8wKsCrsEYY40xLy2NJElsXdcHXhWWIDwcTdNYY8w4m2quK8oY82emCOEBfK8/fd/bJEls27YvPyc8ronw+L+qqsa+18fjYZMksX3fv/wZzRRxC79+VlXV3pcMnIZP/Zn7uX72eDz2vmSsRHhYa7uumy3sUyroXdeNP6vr2uvvAr/Kt/5UVWWT5PWWk+c5a6YuivCw/wbxvlFQqOXRNM1sMxy4E9/6owW2fd/bYRhsWZbMVLyw24dHSLdTnue2LMuXfl2a27izkPqTpukYGEmS2DzPCY4Lu314qMnNgB0QjvpzX7cPD3VFueMYAPxQf+7r9uGhVa4UfiAc9ee+bh8eWZYxWwpYiPpzX7cPD20RDSAc9ee+bv2ta6YIhR8IR/25t1t/65opQuEHwlF/7u3W37oKP/tS7WsYBts0zdhfniSJLYqCOf8XQ/25d1m+dXhomuGdC/8R9LlrG27dhNjW/lqoP/cuy4THjxf+ruvG6ZQ6eOeT5/Npi6JYtNFj0zQ2z/Ov0zbruv5zHdq6Yi/uZ8J52svsXX8oy/OOKsuL36E+IL2mBUiboL37/2fw6+GhjRy191ZRFB8LV13XNk3TVXt1dV03u239N0ecC6+zWTiIaJk96w9l+bMjyvLi8NAJeio802Mkh2EYA+asx0zq+n4xPIZhsGmaer83Ham7RV/tMAzjaXE+dDTp3v3ErI5eZ6/6Q1n+7oiyvKptpQt+t69NURQ2TdPTLiBS4f/FfXlCdvxVP+2WuwP7Hi/atu1hO6vqaQ3L7FV/KMvfHVGWo4WHnhbOfGP+5fDQe/MpyLHOVNAOqu9anUdWNms5AXKtveoPZfm7I8ryqvBo2/Zt4amq6s9ZxWfzq+ERMv/e96lqCfVTz/3uaR/2ETgBcp096g9l2c8RZXlVeLzbjllnFZ/9rAsVyq0L/3RWyKdXmqab/tsah5q+3r1HTWx411c6DMP4Z6ZPVs/nc/z33j0kzPWJ933/ZzBTY2gxuAcP6RwWvadphe/7/u1YnZ4ufQ4+iqXv+5f38u0V80k4Vv0RyvL8ezhLWd4kPKYzC5Y2odQNFvJa01SLUfj1halgTr9U9d/6Vuol1xhyxsK3aYVVVdm2bcetKPRdP5/PsQB/KoBaPOVS/+zcy0fIZ6LrNMaMNxU9oSbJ3w399N1NnzTVyvZ9wotVlvM8Hx/KdDiZ+15Dnrzda1widnhYS1l2HVWW31774r9p51eY+p5nfAaxC78+Czco8jwPam0suUbdFHxafiGtH1VOPVmVZfm1W9I9enQrIZ9JlmWzkzZ8vgeV7ZjdIWtMr0nfu++DyRXCg7L8z9nK8qrw0IW44WGMucwYgr64WNPbNNdc9MQT0lpaUkHdiuHz+32vRxU5ZOqirmXLz9j3M/k0JufzvjX4una9QAxzDyZzT8afbBUeMaeHUpb/c8ayvHpul3vhmuN85kFyV+zCP+2+U/MxdriqaesjpMIt2XohRoXz9e6sCY3JffsepltPnImuTZY8mKy1R3hQlv9zxrK8WXhoau6aVNtzzMOdxRGrMEy/1D0W8qg16FspQj5DjdeErLg9ssK968bQ+/h2TZr0sKRMxy7L0weTvc8S36P+UJb/ObIsv72m1b/g/19YVVWXmjMfu/CrleH21YY0wZdS89b3CcO326JtW2uMsVmWBc0kidFP7GvuZuLujPDpeyjLcqxwZ9v7Sq0Md7AzZGxgC3uEB2X5nzOW5dXhkabpOFPhStsQxy78moXhfqkhTfC1/67ve/LZxM3dckHTAn0rUGg//JbmKlxVVePA4xxNhdTUxtAbzB50U3WDQjeHvW5se4QHZfmfM5bl1Z+EvrCrLbaKeZCN+iGnX5TmVetLjVHp9CTi69PceHcaopq77rhN3/cfuxSO6Id36bN4Pp/jZ9627csq5Lqux64e/Xl3DYD7+XRdd4pyrut0b3oKD50vEbv7ao+DoCjL/5yxLG8SHlcaJJeYhV8VefrlqGvBGBNl9o4KeMjCH30OcwVJTzXTa3U3xPvU2vy0KncP7sKvLMvGm4r7Paiy6bMzxry8p77vx9/hM50zNvVxT7/jx+Mx9gLUdR39OmOHB2X51RnL8m13hfvFIzRVwEP7NY0xUbpmtDHm0TdcbC92/aEsn9/v3DkDuYn9K95tU/CNbgRbPlXtPfsH+4pdfyjL53f78LjSDLFvtAhoia3PQDDG3OIozruKXX8oy+dHePxIeIScefCOVsSveWrrus6maXqK8QHEE7P+UJav4fbhcYbZM2u4g2NbDMJrR+CY5z7j+mLUH8rytdw2PDQjin5MIBz1B7cND03RO/uZI8AZUX9w+/CgWQqEo/7gtuGhLVUAhKP+4Lbf/q+t8QD2RP3BLcNDe0+dbbdU4AqoP7D2puGhFaNnOx0OuALqD6y9aXhojjoLf4Bw1B9Ye9PwyLLs43YDdV2Pu08aY2xZlpdfTAhs5VP90XbhGlDXiYdM6f09twsP9de+m2Kogq//r60SzniONbC3T/VHBw5lWTaeNaLFhFc6KA5+bhEeeZ6PT0qftiuY68vVzyj8uCvf+qPuLPeQKu0xhd9zi/DQKWI6KOedoij+TD+k8OPufOuPNhF0ucGD33KL8PA1V/i/jY8A+O+ku2mrXRsd0uX7mwgPx3SjN/eMYwDvqXvXHQv5dKY4ro/wcBhjxvMJHo/H2Ifbtu34AvCXBtL1oFXX9Rgefd/bsixfxkJwfYSHo21bm6bpS99ulmU/ce4HEJvCwhhjH4+H7ft+rE88eP0ewgMAEIzwAAAEIzwAAMEIDwBAMMIDABCM8AAABCM8AADBCA8AQDDCAwAQjPAAAAQjPAAAwQgPAEAwwgMAEIzwAAAE+x9uZivde1GXIwAAAABJRU5ErkJggg==[/img][br]Damit steht die Methode zur Berechnung von Rotationsvolumina:[br][math]\pi[/math] mal das Integral über das Quadrat der Funktion und die Sache ist geritzt!
Einfluß des Verlaufs Oberhalb bzw. Unterhalb der x- Achse
Welche Auswirkungen auf das Volumen des entstehenden Rotationskörpers hat es, wenn die Funktion oberhalb oder wenn die Funktion unterhalb der x-Achse verläuft
Differenzen von Funktionen: Hohlräume in Körpern
Nun kann man auch Differenzkörper herstellen. In der Praxis geschieht das sehr oft: Beispielsweise bei der Herstellung von Drehteilen bei der Metallbearbeitung (z.B.: die Lagerschale eines Kugellagers).[br][br]Nehmen Sie die beiden Funktionen f und g in der Abbildung unten als Beispiel. [br]a) Beschreiben Sie den Rotationskörper, der im Intervall [2|6] entsteht. Haben Sie vielleicht ein Praxisbesipiel für solche Formen?[br]b) Wie muß man vorgehen, wenn das Volumen eines solchen Drehkörpers bestimmt werden soll? [br]c) Kann dies in der gleichen Weise geschehen, wie bei Schnittflächen von Funktionen? [br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAZcAAAEcCAYAAAALEfkWAAAACXBIWXMAAC4jAAAuIwF4pT92AAAm20lEQVR42u2dDYyV1ZnHT4qdYllpaHEMKwlTFh0WxAGUHVg66zRadpEGi2FLCOvsUo2Ehuxsp0FS7OyOEirubFgMDVnidAhbzBhKF0PWj5hF+XZAhgpFVKy1LaFYEQHbWhxo757nzvOOZ17vnXvnzv0473t/Jzm5d5gP/z7nfc7vno/neYzxr1XbvkVfvWy7du36oafSFk6YMOGUvGK3eOnz3HY79LnDdh5qe9mYsbYvO2znVfu6I+j26zX2db59HRVVnx0oWLpsX6ev1Z4+EC/6CpfJkye/5zFcXvT54fNZn+e226HPHbbzRFunMaMtOBps3xgCyoZDxizYa8yIOPjsQMEirwdDX/OwAhcmIeDCuGYGiqxEWm3f7kCl3U6ki/pbocQdLvc7IDnoAOd+HlbgwiQEXBjXT7YjxoyRFYqsSMIrFNvvs++rtxozJK4+m0s7yCQEXNAHXBjX7Fco9v1m2fKS75eLzwIX4AJcgAu2G4Q2OSOxAJltAdIcAsoWC5TFg12hABceVuDCJARcymRc3zZmaJcx0y1AVoTOUDrs10vlexYoFeXss8AFuAAX4ILtstAmq48jxtTI1WELj20BUPT9StvrjxozDNsBF+ACXIALtutXmwDFrkSmWnAst32rs+W1/ZAxq+z7uZ3GDMd2wAW4ABfggu0yNrkavH/ZstfkqnDoptc6OZi3ryOxHXABLsAFuGC7jE1WIHrTa52A5KC1W3B1WP49nze9gAtwAS7oAy4xtp0CZa6kW3HPUeSm14GGhjclVgXbARfgAlzQBlwyNjl0l6vDcggfPpiX219yaC83vfAJ4AJcgAvagEu/TWChV4eb5Lpw6BylWb4XvumFTwAX4AJc0AZcUjYLjkmSaiVN1uHZ/SWJxCeAC3ABLmgDLr1NgGFXIvMsPNaHgNIq/55tkkh8ArgAF+CCtjKHS7DtZSHSEjqY3yBZh20fh08AF+CC3YALcMkGKEN026s5BJTNkoJFvhfnrMPABYMDF+ACXPJoO6neKAkhw+cotq+WFCyS9wufAC7ABbsBF+CSsQXxKAqQnKs34hPABbhgN+BS5nCRLS1ZiYTzeulV4iWFjpjHJ4ALcMGR0BYjuEhUvG57bQ5lHm4pZuZhfAK4ABccCW0Rh4sFRqWFyZxwSWDJPCz/XohtL3wCuAAXHlTgEkO4yLbXvkceOSJpWEIFtzZKoshS5/XCJ4ALcMGR0BYhuMhZSbDtFWQeDgpuSe2UQldwxCeAC3DBbsAlJnBxkkWudlcpL91222nNSjyScQUuwAW4oA+4ZGyy7WVXJHV626vDTWcvt70kXuXFnTt3Ma7ABbgAF/QBl4xNtr0k5Ur4tpdE0oe3vRhX4AJcgAv6gEu/qxS5JqwACR/Op932YlyBC3ABLugDLp9ocqNLUtq72166SmnSoltDGFfgAlyAC+MKXDI2yd2lq5TW0CplfaYaKYwrcAEuwAV9wKVPk/MSPYh3U7G0y8ol15gUxjX+cJHiOYlQBy7ABX1lDhdNGClXiNeGC28dMub2waS0Z1zLAy4LbN/EygW4MK7ARaEyQevNb3UzENvXBrlCzLiiL9smYLkbuAAXxrV84eKUB24L1UlpkcJbjCv6cmknbd9pe7dJXgAxE4ALcEFfecAlVTVHOUuRWJVC5/diXEukz/7ym7afL2Z/5plnLo4dO/ZKuu/feOONV4qtaYD9so+6Vq5c+fsZM2b8SV6xW+z0eauttra2W567T3zv2Wcv7Hvood8d+NrXLnXanwn6gXvu+cPe73//t7teeIFxjbFPlBKKl1i5sHJBX/xWLnJeovXl3RLBG2WVQlp7fKJQ22Lj9P31ukUGXIAL+uIAl0mTzmmJ4LXO4fx2ObA/ZMy0wd74YlzR11+bYfsJ03PmslcBA1yAC/oirE1WKWONeXXG5z53yQ10lEN7uWKM7fAJ3xpwAS7o81SbrEIk/sSuStbJ6qTGmHdmDB/+kX2/otSrFMYVuAAX4IK+iGmTVUq47ry8H23MTyZPnHgO2+ETwAW4YDcmoWxXKRWyGpECXKG4lNW6SpHU9t6WOWZcgQtwAS7o80ibpK/XA/p2BygdsnJJET0PXPAJ4AJcsBuTUL9QmSpnJ24mYjlbkdxf/RzQAxd8ArgAF+zGJNS3SXp7OaB3t760XsqKro/DB/prwAWfAC7ABbsxCfW0oFRwqPa8HNbPP2rMsAH8KeCCTwAX4ILdyn0SkjxfdqWyKrT1JUW5Zrm154ELPgFcMDhwYRLqtwk0LDzmaEr7PqWC85CNGLjgE8AFuGC3cpqEZOtL66O4t74k3f3CPEbQAxd8ArgAF+xWDpOQHMSnuPXVfMSYmgJE0AMXfAK4ABfsFtdJSKBhIVIvGYjd2JQi1EwBLvgEcAEu2C1uk9BRYypTbH0lk0cO8NYXcEEbcMHgwKXcJyE5iLcQWeZufUmsSoG2voALPgFcgAtwieskpFtfM926KcF5in2tLpE84IJPABfggt0iOQk9//xuScHinqdIpUfJ9VXoGvTABZ8ALhgcuMRMnwXIKDmQ76yrOxMqGTxP0rZ4IhO44BPABbhgtyjok9WIBUtjcJ5y0I6rnKfkIeARuKANuGBw4FJO+uQ8RbMSNzuH9Mk093s2ber02HTABZ8ALsAFu/mmT1KzpDpPkSj64Cqx57YDLvgEcAEu2M0XfQIOyUAcik9pT3WeAlyAC/qAC3DBkfpte40ZoUGPHW7QoySWTBefAlyAC/qAC3DBkVI2ufll+1ILkq269SXnKislbiVT0CNwAS7oAy7ABUfq06TmvHvzy0l1PyomtgMu+ARwAS7YrVj6ND3LajeJpNz8klxgMbMdcMEngAtwwW6F1mcBMs2FipYOXjiYJJLABbigD7gAlzJ0JCfdvZvzqy1fkfTABbigD7gAlzJypKB8cChGZZ1dvdyez8zEwAW4oA+4AJcycCTZ4rIAWeDGqFiorMnm5hdw4bkDLsAFuOBIfZrEqEgiSTdGxUJmVaFzfgEX4II+4AJcYuhIWu3RrZ+yXa4TS616bAdcgAtwAS7YbUD6nJXKDnelIrEr2A64ABe/2p22J4ALcPFZn+b9agii6Z0+G9sBF+DiX7vK9leAC3DxVV/4TEWi6bVO/ShsB1yAi7+t2fYVwAW4+NakONeBhoY3FSbBKmWlhcpIbAdcgEtuv7xJ/kCh+xtvvPFSdXX1b69cubJL4NLfz1ZVVV0shqZB9PM+6mpsbHy1tra2W16xW3Z9z49+tP/AwoVvHZwy5WyntZ28CmT2PPnkfmyXXRewyHOHv8ZO26D0FROCT9n+ZX3PyoWVS0mbbHPJdldwpiIrFoFKqbe/WLmwckHfwFsiRQcuwKWoTWupLAkyFOurnKmMZBICLmiLJlzCoGHlAlyK1jROZZlbS0Vqq7grFSYh4II24ILBgUvWKxW9/eUW6FouB/hMQsAFbfGDS6YGXIDLoJoklLQQmRuKU1ne35kKkxBwQRtwweDAJS1ULEBmhRJKrsgmTQuTEHBBG3DB4MDlE80CZHoIKq2dxkxgEgIuaAMuwAW4DLhZiEx166nYvj6X1PdMQsAFbcAFgwMXWamMk9WJA5WNgynSxSQEXNAGXDB4GcNFMhJrDZXtTjnhusEW6WISAi5oAy4YvAzhIteH9cZXL1Tk8D4fNeqZhIAL2oALBi8zuARR9U5SSclYvDBfUGESAi5oy5e+xEjbp9m+0Nf/J+ACXIzAQ2uqdAQBkIeMWVyoTMVMQsAFbQPRlxhu+0zbF9m+wvbNtu/4uAMX4OKZ3eTsRIpyhWNVCp1UkkkIuKAtnb7EGAWJnVsSq23f0hckvb1Dv8/KBbj4ZTe5Vmz7BucG2Frq1AMXxrVYLTHE9krb62xfcvfdp9+2r+1pQLLN9lbbF9s+2/bqnt/3uwGXMoOLpsBvcVYqGyQocrA3wJiEgAvj2i9MhtleY/s821cpMHoBMnnyhfecFYl8f6mCZ5TtFSaCDbiUCVykVr2eo2x3DuvnFhMqTELApTy0Jc9IqnVra7nt623fnmJFskVXJAsfeeTYEd0S835FAlyAS7IJPCxQ5ti+WaEiCSYXCmwYV+DCuA4aJCP0jGSegmRzmq2tzXoYv0BXMCMi9NwBF+DS1272o1CNpmhJboFpQOQoxhW4MK45gUTOScbaPkdB0ZZmRdKuW1sL9LpwZaYVCXDhYY0EXPZs2tQZOldZZ/skxhW4MK4DAsk422fpQXpr+JxEu8BlrZ6R1Ns+OobPHXApd7hIEKRUfTw4ZcpZBYtcMZ5dinMV4AJcoqNNDsyTILnd9ibb19m+Nc31XwFJo4JEVjFDy+C5Ay7lCheNV5kfFOwSuBwyZoHUXGFcgQu2C2tLblO5sSQdac5J5CB+ia5exhbysB248LB6BxcLkWnuuYoEQe7evPklxhW4YLveVUn1Aw+8/lP72pImKFG2tjba3mz7fNun9tz44rkDLmUIF41XWe0EQbbJAX4UHlTgAlwKBJIhPWceyUDDJbqFtT0UR7JDD+KX6w2vafna2gIuwCXScAlvgVnIbOkyZp6bXBK4AJfysF0yeeNUPXBvTnNOIv+25t57f/6GboVVYjvgAlxCTYt2rXO2wJo6jRketQcVuACXHEBiPzwlJuiqpL94kg16KD9fAxkr8AngAlzStKPGVFqQNDrR9av7u1qMIwGX6NsumfakTm9mpbsGvEHjTeYpeEbgE8AFuGTRZAtMbn0FW2CSskWi7TNdLcaRgEu0bJeMcp+uq43mNKuSIJ5ksW5vjYjT5A1cMHjR4NJpzAR3C0wqQ0ocC44EXKJvu+QqY54GHm5ME+Uuh+4rNRp+6mCTN+ITwKXs4aKFu9xqkFJieCqOhLZowiV56F6jha6a06SVD2qT3KcrmOFlNq7ABYMXFi4WJDMFJkGCSdkCy6XEMI4EXEpnu2SA4iw9VN+Q5tA9uApcr8GJFWU+rsAFgxcGLnJgH8oFtmIwJYZxJOBSnNabf0u2uFZOn/7eOxkKXU0rVW0SfAK4lBVcUhzYt0nEPY6ENj/hkqxTMknTpqwKx5VooGKb3uBaqD87jHEFLhi8iHCxIBnrlhmWQl65bIHhSMClQCCpcFYlTXrwnmpVskZXJVN//OOX9vla7AqfAC6xh4tG2C90YlbyXrseRwIuOcBkmN7K6i+ZY4eTf6smvMXFuMYfLjebZOop0237cdtvAy5+wEUj7FuD1Yr9elEhMhfjSMAlC5iM0niRJXomkq7oVXAdeFyUC17hE/lpApS79X2d7WeBS2nhIttdUmclWK1o/Eo1joS24sGlN6Fjui2uIOJ9mUbGj2Zc0ddf+6rtx4BL6eBiIVIf1K+X2JVCrVZwJOCSBiYtaWJLtuh5Sd5iSxjXEumzv7xJ/kAx+uXLl3d99rOfvSJP2GOPPXYi3c9VVVVdLJamHPt5H3U1Nja+Wltb2y2v6X5m99NP7zmwePHJg3YykP7S3Xe/vefJJ/eXs90ios9bbQIWee5Sfe+JJw4e+O53TxyV7L91dWfPyM0tt9fWnvvNXXf9+hdS10R+lnGNj75SAfFO23/DyqW4KxeJqA9WK3rNuB678Qk3fyuXZHzJWL3JtSJNLq7N+r05BCriE4Vq3cClOHCR7S5J3RKcrRwyZtURY8ZgNyahwbVkuvkaY/7iyHXX/c3v02QIXq8ZhG/vOazHdvhE/ttJ03NjTNpM23cCl8LDRQ7og0STAhcp4JUpezGOhLb+YZLMx7X245tcM9+55pqvfKRwCTIETy92SV7GtXzhUmt6bozJimW37aOAS2HhIiAJEk1KYGQpVis4UpS19caYLNID+G2pgxXHdt14463nfYl6Z1zLDy4DacBlEHC53pglsvUVrFYklUu+ouxxpDhrS0a/T9WU82tTxJi4K5M6p8Y7ZY7xCeASd7hMveGGC/9izIFgtSL1V7Abk1A/MJE8Wws0+n1bikJYLVnk4wIu+ARwiavBZWXSYMwTM6655qMmY7osXBoKHbeCI0VNWx+YrE0DE/n3hgEmdwQu+ARwiaPBZXViYdIuUJn++c//4a+MWYndmIRCMGkOZwt2YHKfHtTnegAPXPAJ4BIng8utL4msD64Y/4MxP6yZOPGcKWCZYxzJd23JCPhMMFmi+bvydQAPXPAJ4BIXg1ugjHKvGNs+yxSwzDGO5Ku25I2ueq2g2JYmL9cSPYAv1NVg4IJPAJc4GFzKDjuR9mudK8bAJfaTUO/14AYFR/jcZKMDkxFFkgdc8AngEmWDaxbjJqfscFPoijFwiZ2+HpgsW/bma2lg0qHp5+uLCBPggk8Al7gY3K0QKauWLmPqUkTaA5dY6EtUB/XfA5hoqV639ntDT24uLxpwwSeASxQNbmEyJ4i0l20w+/XIND8KXCKpT1YcydxbjSlqmiRh8s1vviUrl2nFSPQIXNAGXGJucNnysjBp6WcbDLhEUl8ye/BUjXRPVW1xgxMFPywCtgMu+ARwiYrB5ZA+2AaT9PiHjJmWxa8BF2/1Jcv3zrV9lRbEcmGy1UlDPzKCtgMu+ARwiYLBLUxWBqsV2zd2GpNtaVfg4o2+ZADjdC3fm6quyTrb5+v5SkXEbQdc8Ang4rvB7QplcQAWST6515iB3AACLiXVlzw7qXMP4kPle5fqdtjQmNkOuOATwMVXg9vVyfDQiqU9h7orwKWo+pLXhCdp+pT2NAGM9+nqZEiMbQdc8Ang4qPBJTdYEBQpr1KOOMc/BVwKri9RqWcjq1KsTtp11ZL3aHjgAlzQB1wG1OSg3inotWaA22DApeD6epM/LkqxMtmqKekXFDrmBLgAF/QBl6ybpMUPkk7a18Y8pMgHLnnRJ6uO3nxdW1NAZZke1ldgO+ACXICLNwaXsxQLlGUCFV21zM5TXXvgknNLjPv2t984nqKc73bdAmvQTMJDsR1wAS7AxTuDHzVmmF2ltOqhfYft1XmUBlyyh4lb0rc9lGJlq56dzC5hvi7gAlzQB1yya6HAyPVONmPgUhygDNXD9uWa8NHd6lq/ZMlbr+v5SgW2Ay6MK3CJhMH1RtiW4OBerh4XQBpw+SRQRuoKpCXF7a41miByFJMQcEEbcImcwSWDsXMjrDFP5yvAJT1QRmv0ezhv1zat0Dgr1XYXkxBwQRtwiYzBLVDmBzfC5HZYAcFS5nBJBio2aFqVcL2TJt0OG8okBFzQBlwibXC5VmyhsjRUhrjQrYzg0ptZOFV0fJse1NcM5PyESQi4oA24eG1wuREWpMqX7bAsMxoDl8xAGeokg9ySItVKw2BSrTAJARe0ARdvDS6FvCSTcZDKJc9XjcsQLsmAxll6VpLqQH5+zxkLkxBwYVyBS0zhIleLLUzagqvG/VSMBC7ZrVCaUwQ0thQq/oRJCLigDbh4Z3BZoThXjVsLdNU4xnBJrlDqUqRc2aYBjfX5TgbJJARc0AZcvDa4XbHUSLVIXbEsz1CKGLh8DJSgoFZLaIWyTVOuzA3K/DIJARfGFX1lBRdJjx/EsBThqnEM4JK85TUpxZZXAJTbiwkUJiHggrbow2Wm7a/Y3m37Mdtrow4XC5P6ACxSQdIDaR7DJVGt6VW2hM5QWrU+yjAcCbgwrujLpZ20vU7f32P761GGiwXKTCdd/n0lXrF4CpfEODcOxUkMuV7TrgzHkYAL4wpc8t0+jCpc9j366JFgxWJfF3kkzQO4JMZoYa314cDGxsY3TwR5vHAk4ILtgEsh2gzbH48iXCQg8uCUKWc9BEsJ4ZJMDjlX4062h1KvNOgKZgiOBFywXRnBxf7yJvkDxernzp3be8cdd7x78eLFPel+pqqq6mIxNWXbZcVy6JZb3u2sre3e19j4qm/6Gq2mWqutsQjann56356WlhNHv/71X/18ypTzZ2XLS/qtt77/7uLFb59cv/7Iy88/v2d36PfO+ziuEdHnrTYBizx32C522galr9ggvN72TbZn2hrxbuXi3grb/8ADP/X0g0YRVi5SKz6Zt2tL6KZXxuSQrFxYuWA7fKIQ7Q7bd9p+bRY/6xVcJI7FuRW2wGODFwguyW0vOYDfOJhoeRwJuGA7fKIQ7ZTMUqHuPVzsimVS+PC+POCSDHCsT1ETpVXzeVXiSGgDLsAlas0LuFigjA1SurzsTNjxhUtvGnvZ9tocOphf1nMwjyOhDbgAF+CSd7DEEy4SwJhcjbSFrg+v1QDHoTgS2oALcAEug2ySzVjT5QtYlkXI4AOES2KCrkjcRJHtGvg4BkdCG3ABLsAlT00KfVmwbNDI+xVSUTJecOldpaxLcdurGkdCG3BBG3ApAFgsVNYqWNakAkt04ZK8QrwilCxyXTEzD+NIwAXb4RNlCRcLlGbdCtvYXz2W6MAleUB/u5YAdq8QS82UabmWA8aR0AZc8Angkj1YlipYOixYRkfU4AqX6U16btIROktZ1BOzwoPKJARc0AZcCt4sUOYGYOkyZlw0DS5xKXc9VFl524fGrOtyoLJarxdX8KAyCQEXtAGX7KBwp11xdB9OBtHn1iQRpZM6f2r0DJ6sNz+nZ2Wyruuaa77ykTH/cUATRo7iQWUSAi6MK3AZIFwELPYj+t8NYsUy1ilPPDdaBk8e0Df1PaBf9WxV1YwPjPnCP/GgMgkBF8YVuOQAFwuWhNsH+h/Ya8yIIJZFin1Fw+DJA/p6LRG8PbT1NdOYikX+lznGkYALtsMn/F+5JHL543LF2EJltYKleaBVJItv8GSer9mhxJGyYlkS2vpaCFyYhIAL4wpcSgQXqXevW2Ht/V05Lr3BkwGPC4Iywdo39pOJGLgwCQEXxhW4lAIuwQG+Zjqu9tPgiRpNZ98R2vqalSE2BbgwCQEXxhW4FBsuR4wZ4xzgz/TP4LLFlYyid5NHrhhANmLgwiQEXBhX4FJMuMi5iv35dQqWJX4ZXJJEJqPmt4fAMnqAfwi4MAkBF8YVuBQTLpI2Xw/wN6TLGVZ8gws8Eo0OVDo0sj7X+BTgwiQEXBhX4FIsuMgWmAZKbs2U2qU4Bu9NIrndufnVkIcEksCFSQi4MK7AZbBwyaZpPEuy6NchY24vrcGTUFkVWqkszmO+L+DCJARcGFfgUgy4WKgsT1f0q3gGF3j0OVPZYvvCAqS6By5MQsCFcQUuhYaLBUq9boe1Sa2W4htcYlH6VHrcppmJhxbIbsCFSQi4MK7ApZBwkVLFwbVj+35ScQ2eGK5nKB1ODZVlaQIfgQv6gAvjir6owMVCZWU+rh0PzODJDMXzdNsruE7cVMQaKsCFSQi4MK7ApVBw6TJmnq5Y1g322nF2Bk8mlJTo+TYHKstziFMBLugDLowr+nyEi9wOk+0wPWsZW3iDJ1O1tDpQkdtgk0pkN+DCJARcGFfgUgi4WKg0FWo7rK/BE5Wa+j6Aymbbp5fYbsCFSQi4MK7AJd9w6TJmuoJFVi4FOudIVHznO6/91LkBtrVA14qBC/qAC+OKvlLDRXKHWahs1LOWWQUCi9Sib588+cJ7TlLJSo/sBlyYhIAL4wpc8gkXJ9vx6gJAReJVVgZBkLNmnTnlwRYYcGESAi6MK3ApJFy6jBmnYMl7TIteLe5wgiDn79y5e5endgMuTELAhXEFLvmCi3OIvyOPUBmpq5XgwL4xyFbsscGBC5MQcGFcgUs+4NJpzAS9dtwh15DzBJbZzoF9e89140gYHLgwCQEXxrUs4XKt7afyCRc5Y9FVSx4m1GQlyNZQdP3wCBkcuDAJARfGtezgcpvtJ0x2NViygotz9TgPiSkTc5y0Le39BUICFxwJbcAFn/CnPWf7+HzBRa8et+kh/pxBQGVkqG79kkxZi4ELjoQ24IJPZP7lTfIHitVlNs/0M1VVVRcz/czehx9+5aB9oDvr6s7sev753bloefTRY0dmznzvjMSt3Hrr++8+9tgrh7P83fPFtFm2vbGx8dXa2tpuefVRn692i4g+b7UJWOS5w3b4RGiuL3rLy8rFrljWyqpFklTmIEESTS4N5QMbGYNPG6xc+ITLyoVxLbttsbzBRW6I6VlLx8DPWpLbYKudOitze2ATC4MDFyYh4MK4Apdc4XLYmGaFy/wB/qcnaILJHZoef1LMDA5cmISAC+MKXHKBi0TjB3EtA1u1JOo0wj4IiBwaQ4MDFyYh4MK4li1csmkH+1m1JKPxDxmzOEuoDNG69dsVLHNibHDgwiQEXBhX4DJQuEgEvl25bJOeXTR+osL2Fic1fl3MDQ5cmISAC+MKXAYKF4nCz74QWDKT8RrnfGV0GRgcuDAJARfGFbjkAJeNCpfqDGCxIElsVLBsCBJOAhceVCYh4II24NKnSSp9BctGic7vByxjnTQuq1LlBgMuPKhMQsAFbcAlWLUs16DJRVmCpbHnzKWsDA5cmISAC+MKXLKFi1w5lkN8zSOWZosrmXjSrb0ypAwNDlyYhIAL4wpcsoWLBUudXj9elQYs1Q5YlhcSLMAFR0IbcMEnYgKXYEssdfbjxDA9tA/gUlHGBgcuTELAhXEFLtnAJdgSk6h820PJJSXKPrFWodJSWLAkmm3/wPb3H344cdK+Jjy0G3BhEgIujCtwyQYuwZaY5BNLAZYgAWVrzwqmYGBZbPu/2/4p26+tqUlcAC44EtqACz4RYbhYqKzQW2Kh6PpkUa8gQHJ4YeUkXrL9uuCr3bsTh4ELjoQ24IJPRBsumwUuncY4AElM11xh23sO8wvdEpfcr65cSewCLjgS2oALPhFRuBwxZowGTq53JvrRTnbjuuLISXQDFxwJbcAFn4gJXCxU5vbNJZZMRNn6cSxLsVrioJy1BF/t25d4GbjgSGgDLvhEdOGyWuBiVzA1Osnfp2BZX4wrxw5c+hzo33JL4jxwwZHQBlzwiQjCZasxFVIQTK4gv22M3Awbo2cs2/KZ4XgAgHnQdrkldvp730u8ET6HAS44EnDBdvhEBOAimY/7RuX3boeVfOL88MPEbqvjFHDBkdAGXPCJiMHFrlhmfXzekpimYGkfTHniQaxaztr+Vd0Wu+r++xO/7NkmAy44EtqACz4RNbgsFbg8Z667w0nvMrM0chKi4XDPVlji/W98I/ErgQxwwZHQBlzwiejBZY3A5S9N17cULGsKnZAyBgYHLkxCwIVxBS79wUXyie0zV2/7lPnjEwqXSRgcuDAJARfGFX05t2HGvCyrlibzrWc/zh2GwYELkxBwYVzRN4g23phj+83V/1tj9h0r7VkLcMGR0AZc8InYtC8Z89rj5ku7qszrApfNvpy1ABccCW3ABZ+IcPuGMb9oMo1do8wvXvYhrgW44EhoAy74RAzafxlz/k6z+WejzZs/8ekgH7jgSGgDLvhEhNt/ms9duMW8+OsvmDMvFDeHGHDBkdAGXNAWW7jca/72Qo3Z984XzDurMDhwQR9wYVzRl5c20TzTLXAZYrrvxeDABX3AhXFFX17aTQoXYxL1GBy4oA+4MK7oG3Q7bMzIvzY/+Ogm03nKwmUUBgcu6AMujGsk9ElRx2pv/2eOGlNZa/77ownm0C9LkwEZuOBIaAMuaMtBn4Cly1vA2JXLqJvNju4as/fnPBDABX3AhXGNlD5/AfM98/WZcuYyzfzfT3gggAv6gAvjGjl9AWDMfaanZr0XfbT58+MTzVN/mmpaL/qky+1VVVW+anv96quvvmxfT2K3eOnz3HZnhw0b1o3t8Amn/8BXYB78e9PyZ3zaQBv6sB3aIqXvU7b/q+3PeQsXHAlt6MN2aIuUvusUKs0KGeDCw4o2bIft0DZofXIVud543oAL2tCH7dCGvqxare2nbZeDv+O2z4ooXK6trKy85KEuKaj2ylVXXfUn+3pM7e1Tu3n8+PEfOON/m28GfOKJJ8RuCc9kjVJNbvepSSzapk9/+tN/tK9v236HR9rCdrvikTax0wn1Vx/9YYLtR3Rc/8f2ET7DZZvti/X9P9u+NYJwkQfghIcOLk1uiNXpJ417bH/dM33H29rajuv7OtvPeqbvqhtuuOG3Ho7tApm8Pf4E+ZDtD165cmWXTphvefrpe7HOO740ef7HqLYxtp/yzGyH5QOr6rvJ9g0+w0WMGRzyVGQwpq9wkcOq8Z7CJbyM/dBjbV/V1ZVPrfmBBx54y8Ox3WT73R7DRT4w3OTz9snx48c77ctuz2TJs3a92u16D6HcHfLZCz7DpTvD11GAi7vc9hkuM2x/3Ddtly9flk+3H6j97vFImnxyPKKfvn0bW1mR7tTtkyO6XeGbXzd95jOf+aNOkLf49tzV19efVZ/wqdXqB8CEvvqmTz783azzyT9mmK9L3sL7nZeAS/7buXPn9pqeLUjv4oScT0F32v4bj6Q9ZfuXVZ+XY+t8wj3moV/fr/omKAB9auMnTpx40cMhPeys+Go9nPPkQ8Lr+qFhhY87IW6TySSoKlmRYXIBLrm16++6664zpucQ2NcJMpuVaynG0+dDc9d2lzz0a1efb59wH3rwwQd/5qE7dHtuN/e5u9H0nDV72zqMFJnsaffqp2vgkr8mh6k7T58+vc9Tm53cv3//y/pebrbt9NSRfNwWG+esXHyzmxz0LlJ9N9v+kmf69r/wwguHPfQHmeOCbafJupLx7bmr1a1iWbn8m88Tsty0OqPL6NM6wQCX/LVTnn/6rv3iF7/4O/2EttvH1ZWncJG9+ODK6l4FjE9Nrqg+5ZwJjfdM3yWdIH1rsho4rHY7rF/79mH1l3oVWc5vrzIxaQRRog192A5t6AMuaMORsB3aGFfgwsOKNmyH7dAGXDA42rAdtkMb+oAL2nAkbIc2xhW48LDyoGI7bIc24ILB0Ybt0Ic24AJc0IYjYTu0Ma7AhYcVR0IbtmNcgQsGRxu2Qx/agAtwQRv6sB3aGFfgwsOKI6EN2zGuwIWHFW3YDn1oAy7ABW3ow3ZoQx9w4WHFkdCG7RhX4MLDijZsh+3QBlyAC9rQh+3Qhj7ggjYcCdthO8YVuPCwog3bYTu0ARcMjjb0YTu0oQ+4oA1HwnZoY1yBCw8r2rAdtkNb9OFyre2ngAva0Ift0Ma45qvdZvsJ2xPABW3ow3ZoY1zz1Z6zfTxwQRv6sB3aGNdCNOCCNvRhO7TFfVztL2+SP5DPrgDp7eHvZfr9qqqqi/nWlOd+Hm2x04btsB3a8qiPlQufhNCG7bAd2tgWw+Bow3boQxv6gAvacCRshzbG1ZsGXNCGPmyHNvQBF7ThSNgObYwrcOFhRRu2w3ZoAy4YHG3YDtuhDX3ABW04ErZDG+MKXHhYeVCxHbZDG3DB4GjDduhDG3ABLmjDkbAd2sprXP8fMMk3NyNSIxsAAAAASUVORK5CYIIAZ55d3UonYPuDImBM7MgYuYUVVmQsNoVy0pgZesG3q5HrQYlFYWRFxgYJWEUGAtZiBaw80yasTHawImPkFlZkDBnLUaGIfJV7VsQ6uo2pCCsrMnZWwDZmIGC1w23CymQHKzJGbmFFxpCxHBSKiph7RUxFTDvth5k1vjJ2thFr6xBd8NcPfCyTHazIGLmFFdbcjTqJ1yTel3hToh4ZG7pQoihicZOxzZv/ceEf/uHfOh/72PsPDrECtmHg2iImO1iRMXILK6x5eCFLyDccU27fn2MSTePNl5Cx1IWiVxl5rjfSy7/Lo8AafRnTbcXEHY8t559/Rr6JvePoW59D+LoCNoPJDlZkjNzCCmu+x4/N4I7wKmSnkDH/QjlpzDw9oO8Ssdb+CP0bRFPGHKlxZ5XEbrd0eWSs1a6AXRnUQ/hMdrAiY9QxrPEap5GxwYXSvXhxrVvEeo1p6TZmWpRYoyNjTpG947FB4qDfFuRHP3rm4YaGnzorVvzvG6MoYEzsyBi5hRXW8I5LzcCKGTLmKpTnv/1t50Rx8WH3PZMiYiVRYw23jCWasS6Q2JZKwGwn/MQK2H33dc9isoMVGSO3sEacVb7wNP3iYYpHH310z1tvvXXnUB9XV1d3rX7327JlyzVhY8w2XlyzZlP3smVOT2npsR6Z+HomTmx7tqlpbhRZ586de49O7KXCumLFihuD/vft6nrh8qqqn980deqv7y4uPnNYtxy9MWHCmR9Onfqrbyxe/Ita/XjX51faCaAy6jUMazRDBUxfq/qalWgit7DCOjiMfvEwRWdnp3PDDTdk9LFdXV26KpZ4GzbObOLo3r1Od2WlblEm4nhtrfPc4cOR5RXJduzE7rS1tQX27/nAAyecO+98xfn0p9909NyXX9x66z85e/f2O488cizSNUrENxobG8++XvXX/JsQxOAI1cqY4zjlGzZs+IG8nZfJx8dhZexEZWXNSxMmPK4rYipiJ6ZP74zqilgYVsa2bPmHa+bO/T+3T5z4mza/FTCNkpIznbNm/fsWbVvBT56wsjJGbmGFNWzbtvtMdp3jI31mzP3UpG5NvnDbbc7ze/ZURH3vPnhnxhIH8asktqc5B3ZA4g6J2ZzJgJUzY+QWVljDOKZKdEpcleXnRVbGRMCWuJ+aPDFxYuuRJ56IRaEER8a0x1fiTsiONAJWZy/vHs8EACsyhozBCmtYx/USL0sMp7llJGXM29BVn5rUrcm4FMroyphTIrHadr1P1RF/p8TS4QoYkx2syBi5hRXWoI2fWaHyi9jJmE9D12ZtXxGnQim8jGl/L2eRRL1EZ5p2FHpv5FQmAFhhRcaoY1gZEZWxXmOmeq84SnbWR8byImHJbchUF3Pr+bCtEvNzsQrGZAcrMkZuYYUVGQvwUOkS+dqf6oojZCxnAlYsUS2xQ7uipJCwJoklA1cYMQHACisyRh3Dyoi8jB01plTlyyViHd4rjpCxEUvYTHvY/kAKAdtvz4qVMQHACisyRm5hZcRIxjqNGd9jzI6kiOl5sW6f9h7I2LAETMTKqfFezu2KTitoM5gAYIUVGSO3sCJjMZQxFbFeYxpdT012iZgtiHuhjFzGnCuH6Am2wz4NWcwEACusyBi5hRUZi7GMiXw1uLYmD4mILadQhitjicasehasOc0qmB7Wn8YEACusyBi5hRUZQ8ZUxO5wi5i8v5JCGY6MaauJxFZjR5rD+AuCsArGZAcrMkZuYYUVGQuOiK10i5hELYWSjYxpmwlnuT0L1pWiM/4GiclMALDCioyRW1hhRcbOGSJeVXo2zLUiVt9pzFgKJRMZ03sf0z4Ruc9uVRYxAcAKKzJGbmGFFRkbNLzd9fUpSj3ET6Gkk7FL5ttLuncO0Zh1NhMArLAiY+QWVliRsZRD5Ktc+4e5rzk6ZUwRheIvYwsWLHHGj5/z10J+aIhVsGImAFhhRcbILaywhlTG9PohXamSt+9JvC+CdCQff8l+Y4pVvlJ116dQ3MOZVly8/vCFF97ojBmz9G1jjj7nWQW7Q6KcCQBWWJExcgsrrBGQMZUvkTDHFX+Z67+gngeT/89Ol4h1njRmBoUySMIWJK8oGjdu+6uTJp0jY822O34pEwCssCJj5BZWWCMkYyJfH6iEiRz9jhn4QmNy/ReUr7/V00tsAYVyVsBKJNbYq4jObkEmZWzcuKv+wZjtvy+/N5YJAFZYkTFyCyus0ZSxxIpYvv5y3hYWfcbUUCgJCauwh+47/dpSfPSj6/6nnhnLz0XhTACwwoqMkVtYkbFRlzHP1qSTDymTrzff3cKix5gNFErimqKmFAfyW2zvsPH5uSicCQBWWJExcgsrrLGRsaPGlMrXOzCcFhbRKxTdYkxc1t2SQsJ22Xsiz/77IGOwwoqMkVtYYY24jHmlLJd/IT2wL19zt7uFhT5NGb9C0ZYTg8+D2eiyzVt974lExmCFFRkjt7DCiowNe4h8bXKdEdMGr+XxKhS9gshZK9GW5rLuqem+AjIGK6zIGLmFFVZkbLgiVu15cnJ5fApFV7mc+hR3RbbarcqMVgiRMVhhRcbILaywImPDETHtsN+Z7Z2T4S8UZ6Nr69ErYU0S87NtTYGMwQorMkZuYYUVGctqaDd9EbA2l4jtGumB/eAXirMkxYH8pITNHO5XRsZghRUZI7ewwoqMZTxsh/29ru3Jjv483JUZnEJxFtmO+H4SVpeLq4qQMVhhRcbILaywImMZD5Gvta4Vsa5uYyqiWSiJ9hMtaVbD5ufq/4SMwQorMkZuYYUVGcv0889p7Cq/XhWtQjnbI8yvPUWHxIaBpydzO5AxWGFFxsgtrLAiY0OObmNK5HPbPefExkajULQBa+Ji7lYfCdOWFbWZPhmJjDEBwIqMkVtYYUXG8jJEwLa5RKxdoiz8hZJYCVuZQsJ0dWyVu1M+MsYEACusyBissDJGRcbc/cTyeU6scIWSkLAlKc6E7bN3Ro4t1L8vMgYrrMgYuYUVVmQs5bBtLDpdXfbXhbdQzq6E7U9xcfei0UgqMgYrrMgYuYUVVmQs5dCzYfnsJ1aYQjkrYc0puuVXFWI7EhljsoMVGSO3sMKKjGU13G0stJ/YUWNKw1coiS3HdGfCikY7qcgYrLAiY+QWVliRMT8RKy9UG4v8FIozT2J3iqcjV+Xz6UhkjAkAVmSM3MIKKzI2oqEtK0S+drtWxZry2cYit4WiHfET1xOlkrCxQUsqMgYrrMgYuYUVVmTsnKGH9N3bk/luY5GbQtFmrE69xEGPhHXaPmFFQU0qMgYrrMgYuYUVVmTs7BDxutK9PaltLYJdKLrd6Kyz0uWWsK58dcxHxpgAYEXGkDFYYUXG8iIY+qSkyFfbaG5PZl4oiScka+01Rd4tyQaJqWFJKjIGK6zIGLmFFVZkLDG8T0/2j0Kn/8wKJXE4369X2F6J2WFLKjIGK6zIGLmFFVZkTLcny9zNXeX9lcErFGeGRGOKhq1Lg3g4HxljsoMVGSO3sMKKjGUqYw2FugQ8+0LRw/fOJnsOzC1hB+wF32PDnFRkDFZYkTFyCyusMZexPmMWua47Oqg9xoJSKJWV79T4NG09aA/nl0QhqcgYrLAiY+QWVlhjLGP9xhT3GtPuOiu2Ngig69a9vmTNmn8SQTnzlEfEtobpcD4yxmQHKzJGbmGFFRlLO0S+1rtErO2UMaPcjyuxJblhwoQzjy9e/I5bxnaH8XA+MsZkBysyRm5hhRUZSzm6jalwiZjGklEWsQW2U/4hlTCVseLiM4dtC4uxUU0qMgYrrMgYuYUV1hjKmB7Qd4tYrzGNo3doP9E9v8G9Hakytnnza059/d9fHfWkImOwwoqMkVtYYY2hjGnrCo+MjdI5rMSql7d7fuuyZW+vjkuhIGOwwoqMkVtYYY2ZjHk77esB/lGQsNn2HJj3Hkm9zLs4ToWCjMEKKzJGbmGFNWYy1mdMjUvEDugTlQWUsCLblqLL5wqjyXEsFGQMVliRMXILK6yjNy6QeL2QMqbipVcdjU6n/cQB/Vafxq1L4lwoyBissCJj5BZWWEdPxA5auSqYjHlaWewv3KF9Z6PPalijezUMGUPGYIUVGSO3sMJaqPEJiZMSCwopY0eNKXXfPylRVQAJK/c5G9Y21F2SyBgTAKywImPkFlZY8zneMx9uDxZMxnqNuaOw90/6Pim5M5NrjJAxJgBYYUXGyC2ssOZzzHEbSyFkTFtXSHQlZeykMfPyKGFlVrrcEtYx1GoYMoaMwQorMkZuYY0Aq3zhafrFwxJqLpl+bF1d3bX68Vu2bLkm2/9Pz9Spd/fIBKLx0uTJf5ovnoULf3HLBRec6dKmrcm46KLTzXrXZJZfq9IWSmWY8jmcmDt37j06sZeWlh5bsWLFjRHnjU1eYY1mqIDpa1VfsxJN5BZWWH3cRr94mELlKtOP7erqSny8vs3m/3FEPr67stLplslD48iDD+ac44knnne+/OW/c/QKo2RUVr7t7N7d74QtJ4UOkWzHTuxOW1sb/yYEEeBobGw8+3rVX/NvQhA+bsPK2OA4cdll286uik2ZsivXDH/wB6cWTZz4m3b3atjEiadba2p+9gl+QmFljJ88YWVljNzCGrOVsRCOvJ4Z8/YVkyjP8V9/uc8h/TqJ8ezdc2aMMxmwcmaM3MIKa+xlzN1tX2JvDv/aYyXWe3qHdQw0dqVQkDHyCisyRm5hhRUZ0zsox+p1R0kZ6xnoa5aLv7L8/519ntUwfX8qhYKMkVdYkTFyCyusyJgdIl/L3atiuekrlmji2u4RsY0Dd05SKMgYeYUVGSO3sMIa7ZGVjPUas8+1KrY8ByJW7Tkf1jnQO4xCQcbIK6zIGLmFFVZk7JyhTV1zdwdl4nzYJp8rjaZRKMgYeYUVGSO3sMKKjPmMXmMaXatia0YgYqUSOzwitmvg9ykUZIy8woqMkVtYYUXGBo0+Y2a6rj7q0PYWwxQxPajf6hGxdSNtW0GhIGNMdrAiY+QWVlgjLWMiYJtcW5S1wxSxmRIHXBJ2UKKKQkHGyCusyBgyBiusyFgaGbNNXjtVxHR17Kgxw9hOdOZ7DuprL7EKCgUZI6+wMrEjY7DCiowNIWMiYCtdq2LbhiFiq+0qWFLEtI3FbAoFGSOvsMKKjMEKKyMDGdN+YsNv8urUeM6HteT7oD6FgozBCisyRm5hhTUyMiYCNtu1KtaaXTsLp9ZztdFuiTIKBRkjr7DCioxRx7AyMpSxXmO2Dq+dRULE3CtiOwrxxCSFgozBCisyRm5hhTUyMtZpzPg+Yw4mD+53G1OSoYit8qyINeX6aiMKBRljsoMVGSO3sMIaeRnz3EO5M0MR6/CsiG0f7RUxZAwZgxVWZIzcwgprKGWs15iG7HqLJZq3ekVsLIWCjJFXWGFFxqhjWBlZyphuUWqn/cy3KJ15nvYVh4IkYsgYEwCssCJj5BZWWEMlY33GLHWtiu0dhogVUSjIGHmFFVZkjDqGlTFMGXM/RSmxNo2IlXmuOGqWKBl9LP07ON+U+DeJ0xJ/4TjaaNZxBgIZYwKAFVZkjNzCCmtAZeyUMUXJ6480ThozI42IuS/9bhu4CDwIw3nhQ/EaiA0bnB8gY0wAsMKKjJFbWGENvIz1GbMoKWK9xuxLITtFdhUsKWL6FOWMgIjY56x0/bPEdfb3ri8tdd5BxpgAYIUVGSO3sMIaeBkTCVuflDERs3UphGeD54zYzOAgOY9a6brtnN91nP+KjDEBwAorMkZuYYU18DLWa8xu18rYfB/ZWepp6rogWEiJc2KOt7+ZyNgsZIwJAFZYkTFyCyusgZYxbWGhrSzsqthBbXHhEZ2ZEp0uEasPHpLzvp9wDRQIMsYEACusyBi5hRXWAMuYp6WFp+u+9g0755zY3iC2sGBlDBmDFVZkjNzCCmtoZazHmA0uGav2SE6dS8QODDxNGcThPGala51HxrYgY0wAsMKKjJFbWGENtIz1GtPi39LCqfYc2K8KLpIe3E9I15uupymvKytz3kLGmABghRUZI7ewwhpYGdPzYq6D+wdcclPsuQB8Y/CxnCPePmPJGDPG+QAZYwKAFVZkjNzCCmvgZEwkrMq1RbnNJTYbPR32xwYfy7nAduD/pYTIl/Oy4yS2WZ2PfMT5NTLGBAArrMgYuYUV1sDJWK8x9a6VsVVWamZ47p2cHVZQkbH5+t8rrnBeRcaYAGCFFRkjt7DCGjgZ0wvBB58Xc5pcIrYtJNp12m5JfvbDJyqdK1auHNi63L1br3BCxpgAYIUVGSO3sMIaIBn7pDEfH9xfzFnuErGDwbl3ckgZ25fqvNgll/zakXE1MsYEACusyBi5hRXWQMnYt4y53nVerMnePem+BHxNuLASbSyOS7xnV8pe27vX+fYjjxyLRaEgY7DCioyRW1hhDZmMfc+YdUkZ015j8lubXCK2MxyH9ikUZIzJDlZkjNzCCmtIZexxY3YkZexO8/lbPHdPllMoyBh5hRVWZIzcwgprHmXsqDEPJWVsgvm/X3OJWBOFgoyRV1hhRcbILayw5lHGzhPjOmbM4ypij5jf+l4UV8WQMSYAWGFFxsgtrLAGVsYmu2Tsv5ivPxrFVTFkjAkAVliRMXILK6yBlbF5VsaeMR87PNuc/CuXjC2iUJAx8gorrMgYuYUV1jzL2HIrYw3mCy9dav7hpBWxlig8QYmMIWOwwoqMkVtYYQ28jP2+lbFbzL0/vdj8rNvKWDWFgoyRV1hhRcbILaywFkDGNot5PWWKn7zOPPnGx8w7z9lu+8UUCjJGXmGFFRkjt7DCWgAZ2yvm1Wyqjs8zx35eZN59Ijx3UFIoyBiTHazIGLmFFdaQjzXGXLE30W7/v/21yth/MP/vkShuUSJjTACwwoqMkVtYYQ3k+O/G3Kgytsz85RsqY1HrLYaMIWOwwoqMkVtYYQ30+DNjqr5mpjnzzPNvWRlrjdpTlMgYMgYrrMgYuYUV1sCOdmNqPmtqEzJWbn7ytwMXhFMoyBh5hRVWZIzcwgprQcbDxnz+P5lDCRmbZv5eG74upVCQMfIKK6zIGLmFFdYCjXvM3K8kZewS81qfyFgRhYKMkVdYYUXGyC2ssBZofN5s/uOkjA00fKVQkDHyCiusyBi5hRXWgo07ze/9WVLGLjJvvkihIGPkFVZYkTFyCyusBRxbzMbvJGXsKnPsOxQKMkZeYYUVGSO3sI4i61f1NRErGbvD1LUlZWyhefIbFAoyRl5hhRUZI7ewjiKrithvYiVka82Ohz6UsafqKRRkjLzCCisyRm5hHWXWeAnZ75l7Didl7Abz/Y0UCjJGXmGFFRkjt7AGgHWQkBVLXBzFuMl887jK2G+b59651vzZ2qhyatTV1V3b1dXl6Nsoc2pMnjx5z4IFC1TGnpf3q8grrLAGOjbra1Vfs9OnT7+T3MIK64evDbeQNUk4UYyrzS5HZUxjopnqRJWTIAiCIIhQxgmJp5IrY5OjGEtNa2Kb8jrz6BsLzU3zosqpsWXLlmvU2vVtlDk1Lrvssq/YlbGn5f2ryCussAY6quW1+qy+ZufMmfN5cgsrrGdjk10Z+0zUt3kvvsCUOYtN1Vz2s6PFqi+KhoaGeeQVVliDP/S1qq9ZcgsrrIPOjH0mDnPAxXYZcDKFAiussMIKL6ywBoA1ViKGjMEKK6ywwgsrrEFijZ2IIWOwwgorrPDCCmuQWL8aNxFDxmCFFVZY4YUVVliRMQoFVlhhRcbILaywImPIGKywwgorvLDCCusIhvamOSXxvsRPJb6AjPkXiowKeff1KLOeOnXqa5dccolz3nnnnZF335SI7L2jr776atOkSZOcoqKiX8m735QoikENb7Cv26iO8SZ1A8gojktvueWWx8aNG+eUlZW9FeXXa5q8fhBJWMf5wpQpU5Jz8Wv2e7WJKOuXlFXqWA/fH5H47biJ2O9YAbvKvq89w34msRQZO/cb2Y9+9CNnzZo1P4z4N7K1n/70p5968MEHkz+hzJHolfhSBFm/cNNNNz196NAhFZRyef8rVsgiW8OPPfaYNgb9acRr+JOa15j8lK0/PDwp9bvmmWee0TqeL+8/JtEQoxWUtRHlnbN79+5W/b5jWS+QuFfilgiyfuraa689+cADDyRZ1S0e0B804iRj3zF65/e547MS+5Cxc6x9zaxZs3SyWx3xb2Q/FsZ5nslOhexUBFlfE9ZFLtYxEu9G+ZvYZz7zGUdXPiNew7fpN7GYyJheDL7OIygzzMCKdhxk7EK7ihLF8QOZn2Z56niCxMtRTKuw3uJhvSrKPxz7jRNWqtxjul0NQcbs+MhHPvJrmeCThRLlb2Sp9u5Px4BVf/L8lwj/QLHyiiuuiEMN79ftnZjI2F/qPBzjs0W6aLA6oqj/5iNj4yM6R53W3QkPq/5w/NdxkrF3LbR7ZLpCEKeVseWuQombjOlS8Y+jzKqrgfLud03m5yVDN66++uqX77///jjU8KO61V5aWpo8f6IrCZ+MKOsv9Yfn6urqZ+UHRufSSy/VIya3xWF+0lXtiH+z3nLXXXe1Hz58OPma1VWxXRIrIsj6vs/3HfWQ9+IkY6kOPr6PjKUUlLjJ2J0Sm6PKWlNT48g37nfk3RckrohoWr/Q3Ny8PyY1/K+PP/74n+gZKstaKvEXEiujuKIg8bQen7CComfGdLXs96I+P7W3tzebgW3ayA6tY3Pugwo7I4r6gmfBQ8f1JqIPZmQrY5lsSyFj0WfVLeuOmLDqNuUPJD4VMcypZuAs4H+M8Q8UWsfHI4iqebzewzsnoqzn5HbKlCl6Lu7CCJfx0i9+8Yvfd62M6ffbgxEV0NW6uvvwww8nWfVJyqdNZotCkRlsUyJjvqz2CcMH7MpCXL5p65bsaxHD7JS4KearuyaiE/t7KXjfj3Juv/WtbznLli07bqI9XvE8YKRDH86I4sNUehToy642Htq1QL//nDYxGn4H+C8yHOCPvYzdfffdbfJuBd+0I7F6ki7ikNeonj/ReXq8hzfSZ22U8XOf+5zT1dX1pxH/tvNBjH6o8HvNatutf42TjGnfkjWe39P3v4OMxVPG5CeUhVVVVboy9qmIp/VNYVzi08ajlxoOfV4X+uT1UARZ90p81pNbbQnwZJTn4qVLl+r8dHvE56dXfJ4w1JX7n0aQVc89/o6HdUtU5+JUY4kZ2JZJNn3VvVpdBr0OGYvlN7LrKyoqXnnooYfi8Jh8w6233nrYdSZDz1bp8vgnqeFQj8161kYb3Lp6UXW45rgoDf3m/HLyhwoZ19oaXhHV5GpOL774YmVdGPH5acO2bdse/O53v+t+EEWf+N4QQdarampqnnjkkUeSx2NWWg+5zcRsaOdxfST6AytmmT45h4xFb/zMxGg76/jx4zvLysqcMWPGaO1r+47V1HD4h/YZKy8vT+b1pBl4Miuq46rFixefEFZn2rRpr5sYtLY477zzkt+0TcTreJvkNDn//p3E56LKqs2oJ0yYkGxH82SUf6DIx+CicFhhhRVWeGGFFVZkjEKBFVZYkTFyCyusyBiFAiussMIKL6ywwoqMUSiwwgorMgYrrLAiYxQKrLDCCiu8sMIKKzJGocAKK6zIGKywwoqMUSiwwgorrPDCCiusyBiFAiussMILK6ywImMUCqywwgorvLDCiowhYxQKrLDCCi+ssMKKjFEosMIKK6zwwgorMoaMUSiwwgorvLDCCisyRqHACiussMILK6zIGDJGocAKK6zwwgorrMgYhQIrrLDCCi+ssDKQMV4UsMIKK7ywwgorMkahwAorrLDCCyusDGSMFwWssMIKL6ywwoqMUSiwwgorrOQWVlgZyBgvClhhhRVeWGGFFRmjUGCFFVZYyS2ssDKQMVhhhRVWeGGFFVZkjEKBFVZYkTFyCyusyBiFAiussMIKL6ywwoqMUSiwwgorMgYrrLAiYxQKrLDCCiu8sMIKKzJGocAKK6zIGKywwoqMUSiwwgorrPDCCiusyBiFAiussMILK6ywImMUCqywwgorvLDCiowhYxQKrLDCCi+ssMKKjFEosMIKK6zwwgorMoaMUSiwwgorvLDCCmugxgUSryNjvChghRVWeGGFFdbREbGDVq6QMV4UsMIKK7ywwgprAccnJE5KLEDGKBRYYYUVXlhhhbXw4z2JlfbXyBgvClhhhRVeWGGNDqt84Wn6xYMcjuMsT/5a5SrTz6urq7tWP37Lli3XBJ0xB1FpC6USVlhhhRVeWGEND6vRLx6mULnK9GO7uroSH69vw8ZJEARBEEQ8YlRXxuwWom+k+xxWxvgJBVZYYYUXVlgjszIWwsGZMfbuYYUVVnhhhRVWZIxCgRVWWGGFF1ZYkTFkjBcFrLDCCi+ssMKKjFEosMIKK6zwwgorMoaM8aKAFVZY4YUVVlgDNpAxWGGFFVZ4YYUVVmSMQoEVVliRMXILK6zIGIUCK6ywwgovrLDCioxRKLDCCisyBiussCJjFAqssMIKK7ywwgorMkahwAorrMgYrLDCioxRKLDCCius8MIKK6zIGIUCK6ywwgsrrLAiYxQKrLDCCiu8sMKKjCFjFAqssMIKL6ywwoqMUSiwwgorrPDCCmveWf8/E6GcfCM7qigAAAAASUVORK5CYILScXeHzcjKkXqENZyRVSOvr72+ZEuJ6K3t7rZIDoU/hnPyYycffOpBk1NPnTr1tJvrqq+7rua6eGLzuS1FsZmZLIgNL/Z/O0ZuX3XXXW899pj55Xlj48bgccc4drS3r7qkdoQ+wO4zuxuONNR11XWe7jwf3ntzxooZxo5dD3XNWD5j2tpph88cPnLmiM4j4Zw9cvTsUUnuytz1d6+XREmxTeW25UpsCVW5o1LHY7ipzVNvqr/JdEXqYbZ12e13tku5NqFmQgJvTWqYJA6Wj5OaJwU2ML2XJmKvCfUTxtePH980Pp7kyraXlW4vtRHJ3VB5g9GbvLHIl3ZEUrKtRNLR1WFzbcm1I6pHmL8Prq24dkT5iPeVvM+4ra2rzeR9Ze9r72r35fQnTkuGlw0f3jz8zLNndD5+5urKq4dVDENseBF6w44bN761dOlbNTX/dvastuMbb9gbdCS2o+/mjtjxiiZwKVvgdP8HPvbAvg/vM9P9dzy8Y/+5/bEz/nObc489esyb448ed/Ph48c+fEw+ru9av/7QehGbZErrFMnk1snajh3KDsKV7ywv7/Q7zHZFTmyYKIWartUqxo6uHO0Vm4n9zLi6cdJMPo5tHut+Ugq4baXxIhXbyLqR5j143eYabkeJN++vfv91jdeNKBnxvqr3GcnZLxXvKLYp2lYkWX9kvc2womHm/YtWh5UNk8gfCuK2YTXDOg53SN5b+l6JPj4SlbOfPnv2s2fVEqUWqprba1ShMuHihheht2tHB7d29NjRjE/0wI5mdjh27AtiE/LzTzt5NPWlbF8PE2+N9t1P3r338b3xlrIdP3dccu9j90byuJMndKwebmy9cULrBDdrJ7i143olktBS7Iwq5iQdhzpMxtSNMR2SZZ1lN1TdENdz20tH1owUDd9Qc8O1ZdfKP0u2lyTN+qPrjeS8bnMNt6PIGynUNh7deFXRVVeVXWWKYF8DSeGOwsLthevvWe/mmM70tumS/NZ8ycTlE82B6E1Up2230NWeL/gPL0LfsqPZCiCpHWNvfYwdeya2C9x8xCu2nJyHc3LOTJ36WODmI91ao22n+x//xPFzL5yLt5Ttvo/ed/+T97t5Sn984MkHHnjKjZVExz3abaPXjNaSCzsvdtzR9EyuP7xexxGq2yF5uEM+M6JsRKDeircXj6gacU35NRuObpB67uriq6+uurpoe1FspKXNxns2bjiyQcpZSfHO4qKdRTaFOwttRjeMloioprdPlxixabfNU6PqR/liSjrjQm/so3xeDAx1IV6EPm1HM2G1W3bs37evury7aqUitkmTPmTFduFrtB/6/ENnXzgbO93fzvg/+cxJyYPPPKjz7IPm4NQzpyTmeMOxDTrHN0hxZm3njSvFjfqjMdaGezZEcsTJ0Q1SrpXcWuIVm5twhWfav7f8vX+77G916eaJcZsv1mEiqsAGvsbGi1aNaq5S81WAF0vUpBWTLtSLJVxR8SJcVjvaTVZff/31pHY0V9Ir2o6XUmwXsqtWz8Q2bty5VNaxxS5lO/XCqUXHF0m6Pt1lZvw/9OJD5750LnC6v3eN9unnTts89NxDD33yoYc/+bDNhvs2bLxvo2TDvdptNqI6k2Etw65quUqkKB+LdhS5Hg3H7Y10hDS2aWwCby3ZuUQbpUirToo5tUAl9pzrRcdzidu7TxvtRf0ojxd1j+g85znL1cQVE/Pb8v3xSFGeLbEXuVLhRejTdvRtQd4X7NhjsXndllRsfXxXrXhrtG+44YnApWwJxBY443/bM9tu/cStsdP9Y2f8D6sbduYzZ0we+ewjZz971uZDn/3Qhvs3SLSBNk3XaQ+IWzIaryzUhjPxVmmStEVp8dQY8WKp40WnmEvuxRL9/GLExO3dp431oqdk1F6cr58zwIhO5KsRL5YpOlHxIvQ3O3pvX9UzO9qbWF25YutTu2pZRox4OnaNdmKxxa7R/ug/fPTmh2+edXKWybEvHUv0yy+X8ma1/t71gdEzKqVBsetFtUjJZ3xeTFuYNrZ5rFZLYZQU/V5ckCZqjCdFn0dTqhfLHS/O08ZKUi+uiHonsaOM8uZH1Y2K50XXmotUKp2oXJrwIvQtO/puXxXPjnavHCNInyPtngB2WwC7b453jYedqpOK2HxuuwRiuwS7aiWu2GI3H0lFbFdd9eylX8pmHGNE+PxPn//i61+MeNHozRSL4sWFjhejh9/S5qelLU6LLRa1TXvsxXnJvei2nKs7UdWc4K5UY2vfG5aWVo2RerEwql60valm0qlbXzptKBbxIvR1fv3rXxs7+spHnyPtfnKxqzuMLL2+FKN4lWmsaXfSsfWlV59GbAkmRvZBsfXBXbWUev4y/P47fZJf+PkXNr+wueETDc2fbN7/1f1WimpZxItGjbFedFuKQpaqwE5U25WaqBPV68X4XaPewcWIF+fqei5VL85XUfNo7OBiSXS9uE7HfNUdxXRkT7GIF+HK4Le//e1vfvMbcaRcgn036zD367Cm9O68aueyen1pjGKt6RWn152xBk19mO3SiO1K3FXrsnjRqPGhVx/6zI8/Y8rEZR9dZvWju1KLotSoYwRTrGyltfTWpZJ4g4u2x9VozCe5yKQbrxcXpORF3TjsueClF0UxXpzrloCRR5lO1HX5sfG2TFIsFnEhxYvQ9/jDH/7w+9//3mxp79Wkt6C0sjRlpdeXvvrSYvpjvRhL/TSMV6XdFVtgb2SKYrNu6ze7al0uL7pVo5Oj3zza8ukWt8/wjhozxDh943Sb9SfWR6zpJG1JWlpJmlWjT3IRL85P8xV2uuWisBfLlLfTNYkXS/0SjevF0oAlid6uVP1wpxYM8GL08gxzQvxGXMheNngR+jx//OMf3333XXOHM9Hk7373O2tKI8tYX1plesVp3Gn1aQxqeCuIfw+iB/NHBvJ2kZfRi4aub3Qtfnxxx+c6fMoUFybIoCWDluxa4sYUizEqMhnTNMbbQRo4uJh4iDFw9X2CetFt4JtKE10yuoOL8aXotikO/6Hg2ekGKeJFuGL472isKa0vjTKtNa04rTutQS3vxOdXcWAf5D7uxU/96FMS3ydFjf5SsjZIjdGTV40X4+0aE9WN6ajRTtUJfIg0S1uYFiDFhYl2pYmS4sK4Sy8GzR/kd15J1O5usRu8+eTHlqd4Ea5U/hLNn//85z/96U//HYc/Orzr4Q/RcD77mRcP/v3B2mdrJb7PVz1TFdvLGm8tR4AXixN5cXTjaNNH6i0WAx8izQK3akvgxajV+k53brwlib7V+glWX1AU4kXoh/yfB84GXgzk8DcOH3v52Md/+PFz3zl34GsHAt5bhUrqxcjE1PhqFC9qNYoUdywxiVdf6pJxUVqAF0uD23tX6ycoFv0LExOuvmCuKV4EgAHqReHEP55Y9elVt3zxluD3Jv6oT6JGd8bNRmel4+LgsT2J14uJ+129G3xLs8U7FidqvMBdaJiKF93+0gXK24lKsQh4EQAvduftJd4cx8xe2ZgvUUucg3hCEinuihSLCYpLM3/V14maeLc2d0Wj7URdlx9vAYaehjqXYhHwIgBevAhq9C52NGp0EyRF+TioZJAUf6b+S9Lb6ZSMkWUhJfG9ODe8W9tCFW89om9hotGnWhqsRvfdsjARLwIAXkyixkoVK0V3DcOyKC/a6Z2uuowUFw8aVDzIWieJF+dGdg9IRaJ6E9fCZF70zri5oyZ2VSILE4H/8QB4sZtqjI6xi/ul5Sq4mvRMalWLdeWX2HNmk1K7MWmKEo2sNbxdezqxFCNedNQoUo8s2ECKeBEA8GJvWTPpog7txfD+q4lV51aZy5IXi5HGhVGLESMDigv9y/mtFGNlz08jXgQAvNh71WRFCjNXw5N0kntucQpdo3bgMOHu3uxoCngRoE9w7twA8mJSNXo7MAPU6JNcYWSJoZ50k3AqTWSkc6EuMVl6AXgRoC+yb19oypSB5cVQ+PZVsXa0I4XGi3aejtkNIFZydlmka7uSuDe+MA9xn9bsYhq0MBEpAl4EuJwcOhTati00atSA82LIjtiVKrVCeWffeAf27BRWYzJfmegrLo0aExWLRVHPHHD7C6QIeBHg8vLcc/rjwPRilB3jz2cxN5lK2uNqvahXYoRvamGnmMa2jDyECTWAFwH6GgPZi91wZ5WKXdoR4Lkl4T7VhYpVhoAXAa4ADhzQeeABvHhBlWVS22FEwIsAVwZ33qlz3314EQAvAkAQeBEALwJABG+faqAOlXonOm9x0gDwIsBA/Q3UXrR5QalX8CIAXgQA+lEB8CIA4EUAvAgAeBEALwIAXgTAiwCAFwHwIgDgRQC8CAB4EQAvAgBeBMCLAIAXAfAiAOBFALwIAHgRAC8CAF4EwIsAgBcB8CIA4EUAwIsAeBEA8CIAXgQAvAiAFwEALwLgRQDAiwB4EQDwIgBeBAC8CIAXAQAvAuBFAMCLAHgRAPAiAF4EALwIgBcBAC8C4EUAwIsAAAB4EQAAAC8CAADgRQAAALwIAACAFwEAAPAiAAAAXgQAAMCLAAAAeBEAAAAvAgAA4EUAAAC8CAAAAHgRAAAALwIAAOBFAAAAvAgAAIAXAQAA8CIAAABeBAAAwIsAAAB4EQAAAC8CAADgRQAAALwIAACAFwEAAPAiAAAAXgQAAMCLAAAAeBEAAAAvAgAA4EUAAAC8CAAAgBcBAADwIgAAAF4EAADAiwAAAHgRAAAALwIAAABeBAAAwIsAAAB4EQAAAC8CAADgRQAAALwIAACAFwEAAPAiAAAAXgQAAMCLAAAAeBEAAAAvAgAA4EUAAAC8CAAAgBcBAADwIgAAAF4EAADAiwAAAHgRAAAALwIAAOBFAAAAvAgAAIAXAQAA8CIAAABeBAAAwIsAAACAFwEAAPAiAAAAXgQAAMCLAAAAeBEAAAAvAgAA4EUAAAC8CAAAgBcBAAAuLv8f+/rDSvtHkSQAAAAASUVORK5CYIK60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIrusI81IYZjxW6oisNw4w7i67oiq4wD7VhxmOFruhKwzDjzqIruqIrzENtmPFYoSu60jDMuLPoiq7oCvNQG2Y8VuiKrjQMM+4suqIruj7WN790A2Q0Z3/cAAAAAElFTkSuQmCCw+PuOtAdmgPdNdO+kP97cq1JP99Xw9czfOFCA92hOdAdmiuA4cvwZfgyfHm/ojs0pzl01xcPhqVh6JSMz09OP3+4hq9n+MKFBrpDc6A7NFcAw5fhy/Bl+PJ+RXdoTnPori92haVh6OKMzy9NP99Tw9czfOFCA92hOdAdmiuA4cvwZfgyfHm/ojs0pzl01xfLw9B9GZ/fl36+pYavZ/jChQa6Q3OgOzRXAMOX4cvwZfjyfkV3aE5z6K4v4u+59VRYGoduTc669M+vS/94+ffjOrqGr2f4woUGukNzoDs0VwDDl+HL8GX48n5Fd2hOc+iuT64JPx+ZJp13TPg5eaPUar5eOMy/xkoZvnChoTvQHLqD3jdn+DJ8Gb4MX96v6A7NaQ7d9c1Fybk3OfuT82z6Y/zj8zL+9dNGqcP9eqv5a6yE4QsXGroDzaE76H1zhi/Dl+HL8OX9iu7QnObQHd1g+MKFhu5Ac+gOet+c4cvwZfgyfHm/ojs0pzl0RzcYvnChoTvQHLqD3jdn+DJ8Gb4MX96v6A7NaQ7d0Q2GL1xo6A40h+6g980Zvgxfhi/Dl/crukNzmkN3dIPhCxcaugPNoTvofXOGL8OX4cvw5f2K7tCc5tAd3WD4woWG7kBz6A5635zhy/Bl+DJ8eb+iOzSnOXRHNxi+cKGhO9AcuoPeN2f4MnwZvgxf3q/oDs1pDt3RDYYvXGjoDjSH7qD3zRm+DF+GL8OX9yu6Q3OaQ3d0g+ELFxq6A82hO+h9c4Yvw5fhy/Dl/Yru0Jzm0B3dYPjChYbuQHPoDnrfnOHL8GX4Mnx5v6I7NKc5dEc3GL5woaE70By6g943Z/gyfBm+DF/er+gOzWkO3dENhi9caOgONIfuoPfNGb4MX4Yvw5f3K7pDc5pDd3SD4QsXGroDzaE76H1zhi/Dl+HL8OX9iu7QnObQHd1g+MKFhu5Ac+gOet+c4cvwZfgyfHm/ojs0pzl0RzcYvnChoTvQHLqD3jdn+DJ8Gb4MX96v6A7NaQ7d0Q2GL1xo6A40h+6g980Zvgxfhi/Dl/crukNzmkN3dIPhCxcaugPNoTvofXOGL8OX4cvw5f2K7tCc5tAd3WD4woWG7kBz6A5635zhy/Bl+DJ8eb+iOzSnOXRHNxi+cKGhO9AcuoPON7fj7HDCaBi2LQ7DdZPOaBC+NpoLNxi+DF+GL8OX9yu6Q3OgO9rN8IULDd2B5tAddL65+blwzmgY/jF+V9ekszgI/9SW8cfwZfgyfLnr8I4FzaE7yGb4woWG7kBz6A4631wcvhaH4cYujD+GL8NXS579p6NBeCjrJD//EXcd6A7NoTvdUQbDFy40dAeaQ3fQ+eYMX4Yvw1fl3/H13PyZYWPWST7f564D3aE5dKc7ymD4woWG7kBz6A4635zhy/Bl+GrYs7fkH4Xo/Yru0BzojvYxfOFCQ3egOXQHnW/O8GX4MnwZvrxf8Y4FzaE7+sHwhQsN3YHm0B10vjnDl+HL8GX48n7FOxY0h+7oB8MXLjR0B5pDd9D55gxfhi/Dl+HL+xXvWNAcuqMfDF+40NAdaA7dQeebM3wZvgxfhi/vV7xjQXPojn4wfOFCQ3egOXQHnW/O8GX4MnwZvrxf8Y4FzaE7+sHwhQsN3YHm0B10vjnDl+HL8GX48n7FOxY0h+7oB8MXLjR0B5pDd9D55gxfhi/Dl+HL+xXvWNAcuqMfDF+40NAdaA7dQeebM3wZvgxfhi/vV7xjQXPojn4wfOFCQ3egOXQHnW/O8GX4MnwZvrxf8Y4FzaE7+sHwhQsN3YHm0B10vjnDl+HL8GX48n7FOxY0h+7oB8MXLjR0B5pDd9D55gxfhi/Dl+HL+xXvWNAcuqMfDF+40NAdaA7dQeebM3wZvgxfhi/vV7xjQXPojn4wfOFCQ3egOXQHnW/O8GX4MnwZvrxf8Y4FzaE7+sHwhQsN3YHm0B10vjnDl+HL8GX48n7FOxY0h+7oB8MXLjR0B5pDd9D55gxfhi/Dl+HL+xXvWNAcuqMfDF+40NAdaA7dQeebM3wZvgxfhi/vV7xjQXPojn4wfOFCQ3egOXQHnW/O8GX4MnwZvrxf8Y4FzaE7+sHwhQsN3YHm0B20vrlbzwm/tDgIl2WdhWG4Pjm3Gr4MX4Yvw5f3K7oDzaE7us3whQsN3YHm0B20vrn59eHE0TCMk7Mt43x3cRj+zvBl+DJ8Gb68X9EdaA7d0W2GL1xo6A40h+6g9c3F4Wsh57/E79L4Y/gyfHVk+Hoi/uc269xyVjjOXYd3rO7QHLqD1TB84UJDd6A5dAetb87wZfgyfLVu+BonX+ORSSf57PvJ+S93Hd6xukNz6A5Ww/CFCw3dgebQHbS+OcOX4cvw1Z1nnz8zbBwNwkPuOrxjdYfm0B2shuELFxq6A82hO2h9c4Yvw5fhy/Dl/Yp3LGgO3UFk+MKFhu5Ac+gOWt+c4cvwZfgyfHm/4h0LmkN3EBm+cKGhO9AcuoPWN2f4MnwZvgxf3q94x4Lm0B1Ehi9caOgONIfuoPXNGb4MX4Yvw5f3K96xoDl0B5HhCxcaugPNoTtofXOGL8OX4cvw5f2KdyxoDt1BZPjChYbuQHPoDlrfnOHL8GX4Mnx5v+IdC5pDdxAZvnChoTvQHLqD1jdn+DJ8Gb4MX96veMeC5tAdRIYvXGjoDjSH7qD1zRm+DF+GL8OX9yvesaA5dAeR4QsXGroDzaE7aH1zhi/Dl+HL8OX9incsaA7dQWT4woWG7kBz6A5a35zhy/Bl+DJ8eb/iHQuaQ3cQGb5woaE70By6g9Y3Z/gyfBm+DF/er3jHgubQHUSGL1xo6A40h+6g9c0Zvgxfhi/Dl/cr3rGgOXQHkeELFxq6A82hO2h9c4Yvw5fhy/Dl/Yp3LGgO3UFk+MKFhu5Ac+gOWtHcaBjGyXk84+xPzr8Zvgxfhi/Dl/cr3rGgOXRHvxm+cKGhO9AcuoNWNDcahoeNP4Yvw5fhy/sV71jQHLqDPIYvXGjoDjSH7qAVzRm+PLvhqx/D1/bTw+uSH/8l+Wtcl3GuX5gLW7xf8Y4FzaE7mMTwhQsN3YHm0B20ojnDl2c3fPVj+Eq/7sH5uXDJpJN8tm00CF/xfsU7FjSH7mASwxcuNHQHmkN30IrmDF+e3fDVn+Er79nj+LUwDLu9X/GOBc2hO5jE8IULDd2B5tAdtKI5w5dnN3wZvgxfeMeC5tAdTGP4woWG7kBz6A5a0Zzhy7Mbvgxfhi+8Y0Fz6A6mMXzhQkN3oDl0B61ozvDl2Q1fhi/DF96xoDl0B9MYvnChoTvQHLqDVjRn+PLshi/Dl+EL71jQHLqDaQxfuNDQHWgO3UErmjN8eXbDl+HL8IV3LGgO3cE0hi9caOgONIfuoBXNGb48u+HL8GX4wjsWNIfuYBrDFy40dAeaQ3fQiuYMX57d8GX4MnzhHQuaQ3cwjeELFxq6A82hO2hFc4Yvz274MnwZvvCOBc2hO5jG8IULDd2B5tAdNKK50SDcPBqGz2edxWF43Phj+DJ8Gb4MX3jHgubQHeQxfOFCQ3egOXQHjWhuNAyPx/9CO+sknz9j/DF8Gb4MX4YvvGNBc+gO8hi+cKGhO9AcuoNGNLc4DN8w/nh2w5fhawXD1+8uDMPXkx/PyTo7zg4neL/iHQuaQ3f0k+ELFxq6A82hO2hEc4Yvz274Mnyt+NmHYTwahL2TTvJzn07On3m/4h0LmkN39JPhCxcaugPNoTtoRHOGL89u+DJ8FfLsg3Bl8vOv837FOxY0h+7oJ8MXLjR0B5pDd9CI5gxfnt3wZfgyfIHu0By6g1kZvnChoTvQHLqDRjRn+PLshi/Dl+ELdIfm0B3MyvCFCw3dgebQHTSiOcOXZzd8Gb4MX6A7NIfuYFaGL1xo6A40h+6gEc0Zvjy74cvwZfgC3aE5dAezMnzhQkN3oDl0B41ozvDl2Q1fhi/DF+gOzaE7mJXhCxcaugPNoTuopLnRMFwe/8vonPMj449nN3wZvgxfeMfqDs2hO5iF4QsXGroDzaE7qKS50TB8b34uXJJ1ks8PGH88u+HL8GX4wjtWd2gO3cEsDF+40NAdaA7dQSXNjQbhIeOPZzd8Gb5Kf/YN4ZPJz/+LxUG4LOvsHIRXer/i13WgOXRHNxm+cKGhO9AcuoNKmjN8eXbDl+GrqmdfWPoO0m0ZZxzHL+9X/LoONIfu6CbDFy40dAeaQ3dQSXOGL89u+DJ8NeLZh2Gb4Qu/rgPNoTu6y/CFCw3dgebQHVTSnOHLsxu+DF+GL9AdmgPdUTbDFy40dAeaQ3dQSXOGL89u+DJ8Gb5Ad2gOdEfZDF+40NAdaA7dQSHN3bo+vGR+fTgx6ywOw98Yfzy74cvwZfgC3aE50B1lMnzhQkN3oDl0B4U0tzgM94/mwl8vDMPtk85oGMbGH89u+DJ8Gb5Ad2gOdEeZDF+40NAdaA7dQSHNLQzD7vkzw0bjj2c3fBm+Gv7sn0u+/s44fmWd5F93rPcrfl2H5kB3tJPhCxcaugPNoTsopDnDl+HL8GX4asuzJz/+e/LXuHHSid+dOj8XzvF+xa/r0BzojnYyfOFCQ3egOXQHhTRn+DJ8Gb4MX5149kHYa/jCr+vQHOiO9jJ84UJDd6A5dAeFNGf4MnwZvgxfhi/w6zo0B7qjboYvXGjoDjSH7mBFFofhI6NheDz58Ru7zj32sT1vPmMcf4x/HM9oLjw7PwgXGX88u+HL8GX4Ar+uQ3OgO+pi+MKFhu5Ac+gOVmRxGK6bnwuXTBogjD+e3fBl+OrKsy9uCA8kf/3rFwfhsjsuv2DnPTd+eBx/jH+8fG45LRztrYBf16E50B3NZPjChYbuQHPoDlbE8GX4MnwZvnrx7MPwRHK+m5xtt116xv13Xv2Wcfwx/nF6xvPrw4neCvh1HZoD3TG71yfnnuTsT87B5OxLzt7kbJrhaxq+cKGhO9AcuoNDRsNwbPzHe2Wdxbmwe34Q3m74MnwZvgxffXn2SXdd8vf2iOELv65Dc6C7Ah3R1wd/Z1gaqLLOFav8uoYvXGjoDjSH7uCQ+I/vGg3CjxeG4fZJZ3EYDub9l8HGH89u+DJ8Gb7Ar+vQHOjusFybnLuSs6ZvD35kcp4KSwPVjuSclP75dcnZnf75+PlqVkHDFy40dAeaQ3dwSBy+dgzClSsZQAxfhi/Dl+Grr8NXcn6anJ8k5/GMM/ZGwa/r0BzobgXiphNHr3Ho4fi1PE7dnfH5o+nnb5zhaxu+cKGhO9AcuqPjdg7CKxeH4f6FYdg96YyG4TvJ+azhy/Bl+DL+ePbc7/jKf/ZheNwbB7+uQ3OguxWKY1cvx6896UNfnPH5lvTz7av42oYvXGjoDjSH7uiJ+Pt0LQzDF+bPDBsnndEgfG2lA4jhy/Bl+DJ8Gb4yn+9nyX36UOYZhu95I+HXdWgO3enueXo5fi1/R9epGZ+fmn7+zVV8bcMXLjR0B5pDd3TEjrPDCfEfsZX3j99amAt/W8QAYvgyfBm+DF+Gr8zney7rf2Bw6H9kMAxPx/8hQtZZPCus90bz6zq/rkNz6K53ejd+7U8fNutBX5R+vn8VX/u05Hwi/RFcaOgONIfuqNktZ4Xj5teHE7POlGFrf/pj6QOI4cvwZfgyfBm+VvnsyT2efI0bJ53k5+4dDcJT8fdczDrJz/9tb0u/rgPNobtO6tX4dTB90Dzx8wOH+XVfHZa+08txKjubN2/evnXr1nH80b8fju4czTmO7so6p784XJF1Nrwk/P5rjwl/mPX5xpeGD5z90nB11ue/87Lw8Tf9avj0hceH6yad958Udr3vFWH0nhPD9kln25nhsRtOD/+QdUaD8D/XnhYezToLg/Dfv350+L1J5y0nhBs/uyH8R9bnH3hV+FL862d9/snTwiPxZH0ef278GvH/fvuFb/j8dR+6ahx/XP48/rXj30PWz58fhJ9kfTbr51U++6Tj2at59l/sLv595T17fK68Z4+f5T17/Np5zx7/3vKefWEYnst7trzP49fN+/fGs1fz7JPuurKfPQ5jHz4lfHXS+dP14Ufx85s2hCcnnfjZZ84I37n6VeHOSeejvxHuveykMJ/1Dkv++p/Je0e+9tjwwfUvCX+Q+fkvhw/mvYN/LXlGv07x6zpHc46ju9zztuQ88Lzx64iuDl/jFQ5fz67ki6X/C1HHcRzHcRzHcWo6f3x69omff/BV2Sfv82tPzf/8M2fkf37T+vzPb94Qxp/dkP35/CCMP/Xq1f29z/q5Z+/ns8/6bNsH+Z8vDPKfPf7csp697P+/evZuP7vjOI7jtPG86Vf+bwvp+/mj5DwRvzGuy9/xdaCk7/g6zXrqVH3Wrl377rjiH3/88e/174ejO0dzjqM7R3OOoztHc46jO0dzju6cid/xdWeXv+NrX8j/Pb7WpJ/vCwAAAAAAALTN83+PrztDx3+PrwfTBz0l4/OT088f1gUAAAAAAECr9Gr0inalD3txxueXpp/v0QYAAAAAAEBr9G70it6aPvB9GZ/fl36+RR8AAAAAAACt0MvRa/nBn0of/NbkrEv//Lr0j5d/f6+jNQIAAAAAANB4R4Sejl7LrkkfPuu8QyMAAAAAAACt8YnQ09Fr2UXJuTc5+5PzbPpj/OPztAEAAAAAANA6R/i3AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAgML8L8HNNNtdk3jUAAAAAElFTkSuQmCC3zvfN6/ctdJbYE2mxecXXkt2vFVcUC91W/e0nQnqdJqwYsWKFStWrHgzlno1Vwf0DjW7W1Bvc//dklH0ghs0qZ43neaX834hfxVtmZGQ+T61KSOZzabzP9gNaQn1mAkZk7vdX0JDQs3J5S3ooL5SnqPT6XyCD2q3dm01v/f0a7tlGrn3e2+JePw502ZvRtynwRw7m0M+c7PMa3yYtq2hd0y8nTJdOls9kscxWdLjreKCejnautB2Djlf6M9rw+V2lctJlqqBfF6xYsWKFStWrFirzSsj5fVqmxvMJaD7Qb1BNcV5sbgiB7ojee1znf74o7p+E3kfLyB96m4DV6/WuCGtQd1qHr/HvU2uG/ZuOxa5wnSgtDvtP5f3r8tUPqhpv/cd7jXG8ruVQOqF0mXuiHO21b9zCereazS5IVGmRkvY9YJbi1n3oC30mujuq4lnr/nvRlCy460ig3o52rqQdu56/m/dFf117be233dyqYr89P/N1O/c9uI/VqxYsWLFihUrVou93mJxP3ZHev0p7hLQp+vO6Fx1Dw3arRPd6XbSC53260+dz7bYl0yhlXUAZAXv4BRauaZYrnOXAJDnAmsTtk/4ZNJTkzgxZf69j9O/303u4nVefVQ1qiFFfWPegnAtl19DXi+hxvfqSalEx1vFBvVytHUR2pmOBFasWLFixYoVa7V6G9QE3YHcFbgO/bDuJCfUDzLso16tDZpUNxR8fbpfvOnvX7iLd5W7SDDR73/Lq1s4MWGt5HPSXWUJ6rQrVqxYsWLFihUr3oor3lZF69190FNDelJHSW+xuPR91KutQWUxKZkiu1KNNEHd34d5bY9eUKbWytTVcl9vmlS7Rz87+l84MWGt6CLT0COm79OuWLFixYoVK1asWO3zdk1zPxgI6HvdKaddpbqDujdt9WK3heO863W/KWgf7e5BpEY/5xn9XBvKhvRWo77oOM5yTkxYsWLFihUrVqxYsWLFWylFwmdwmrvUhFoVsgJxtQf1OSmrLS8w22N96y4SVYyyUk1zR9WlTcpRvPUHDnBiwooVK1asWLFixYoVK95KKN6+x0u6LRbnXYu+XQfF0RkeVd1B3du2Sla7fsJdAdv7ne0pcnhe16Pr3XMt0vZJ9Yl82cCJCStWrFixYsWKFStWrHh7uzSoO8yU7e6Lxcn09+g90blGXa4hr1eN7nXq9SVa/V6+LEmql0qGk+vsk+q0WXeAExNWrFixYsWKFStWrFjx9mJAv85dLC44zb1e/cQPbVkKQb1cRa5VL9aU+tQilzMk1Fup7c2JCStWrFixYsWKFStWrHjLXWSUXPZDTl8sbr87upp7IahjxYoVK1asWLFixYoVK1a8PSpyvbk3lTp1BL1D/3tSLVP983w2gjpWrFixYsWKFStWrFixYsVbUJEQLmE8uCd6vdqqfw4t8FkJ6lixYsWKFStWrFixYsVafVYnpFZ6qbD3nFT36kD+aiCgH1Ir1ewsi8UR1PmwYsWKFStWrFixYsWKFStBvWhFFgirV81pi8Ul1UbVWJRwTVDHihUrVqxYsWLFihUr1uoN6rH09s77l1Fy2VotuCe6bMGWUHf3cBSdoI4VK1asWLFixYoVK1asBHWCes4loYbrgL4jZLG4Ve5WXMUtBHWsWLFixYoVK1asWLFiJagT1EOLLBaXVI+ELBa3zQ3vpSkEdaxYsWLFihUrVqxYsWKt3CKDtet0/UDX87pe1LVT17d0bXAcZ2SJg/piXX9tXvOSrud0bdN1XA7PO87c99uU9y1/H5Nyf9le/LC57YJ5/j263tT7QT2pZujaFgjoB3WdW8Rp7gR1TkxYsWLFihUrVqxYsWKNTxmk68cqfBE1t06cOPHUb37zm1IE9QG6vh3x2hKqH4p43kXmPmGP7TQh/rGI5//a5NVeCOoyUp5UW0IWi1uvVruNUupCUMeKFStWrFixYsWKFSvWyiy7TV6T0fQZutaYf7/CBOE/yu3Lli0rRVA/nBKYG01wlyKzvVvNbefN38Oe96L5kmG2rrXmvYvhrLn9ixTbPeZ2qfN0/dLctru8QX2R/sWGT3PfpRrUhDI2PEEdK1asWLFixYoVK1asWCuzdJq8NjDD7bfK7TfeeGOxg/o0c5tMWR+d4T77zH12ZnjeU0qFrrE2L+U+JzI89yxz+9nyBfWEhkog7x7QD+ufdSWe5k5Q58SEFStWrFixYsWKFSvW+BR/6vjkElijgu4ec9uGiMePNPf5MsPzLs7wuNqU+8zKcp+LpQ/qslhcQsfx4Ch6Qm3WP4f2UsMT1LFixYoVK1asWLFixYq1Mst7qut6cBnBflip7pdIlyio+9fFTyrgPfvPOziH+9Tk+/6KG9STaqqu+wOj6Id0SL+/F0bRCepYsWLFihUrVqxYsWLFWvlFgvJ5lb7Q2mnljXovcBxnVAmC+vkcgnQhz9vj+xQvqAf3RPfqk6qxIsIxQR0rVqxYsWLFihUrVqxYK7fIdeiypdnFkMDu9OvX77umpqZiB/WehOCYBPXuAX2PWqVur6BGJ6hjxYoVK1asWLFixYoVa+UXGd2+T9cW5e1r3m3rs1OnTj1TxEBdBSPq/jT3pFrirvZeWYWgjhUrVqxYsWLFihUrVqzxDO6zpk+f/pFkuiFDhnxRxED9qbltYsTj+5n7nItnUG9QTRUyzZ2gzokJK1asWLFixYoVK1as8Sn+fuI3ZUyzjjNWftTW1n5fxKDub73WHPH4JeY+B+MZ1Cu7ENSxYsWKFStWrFixYsWKtTLLbhW+V3lqUHf3JR8xYsTnRQzqM8xtX2f4kkBmiv/B3Gc+QZ2gzocVK1asWLFixYoVK1as1WIdrbquRT+g6xTVdd34AF2XDxo06N/l9j/96U8tRQzqUo6Y28/qulR5e5sr8x5OmNuOFzOEE9QJ6lixYsWKFStWrFixYsUah7JIZVjx3a8LFy4s9qrv/hcBJyJe9xOTJys1qD+tvOn5BHU+rFixYsWKFStWrFixYsVa9CJbtMm+6WeUN8Iuwf0rXdsdx1lUgn3UU0uj8kbOZSX4S8pbaG6D8haTK2oIL3JQl5D+57iGdYI6VqxYsWLFihUrVqxYsVafNZZTx/Oc+h7bsE5Qx4oVK1asWLFixYoVK1aCuo1BPbZhnaCOFStWrFixYsWKFStWrAR1W4N6LMM6QR0rVqxYsWLFihUrVqxYCeo2B/XQsN7fBOJKrOMN7rYKfo9FqU1NTXd2dHQ48hMrVqxYsWLFihUrVqxYq9watpJ7pXt7+p4bU8P6RhWxlD6VSqVSqVQqlUqlUqnUstSPdH3XH1G/vkLrbebNjqvg91iUunbt2snyTZP8xIoVK1asWLFixYoVK1asVeddZUbU/1ulT/HnGnWsWLFixYoVK1asWLFixWq7d0lcQjpBHStWrFixYsWKFStWrFix2u6NVUgnqGPFihUrVqxYsWLFihUrVpu9sQvpBHWsWLFixYoVK1asWLFixWqrN5YhnaCOFStWrFixYsWKFStWrFht9MY2pBPUsWLFihUrVqxYsWLFihWrjd6n4xrSCepYsWLFihUrVqxYsWLFihUvQZ0GxYoVK1asWLFixYoVK1asdnn76Nqi6yldL+h6XtePdG3W9QqCenSDbtiwoc2YbS0D29vbf37LLbc4V1555X/ov1/U9Yyum3UdZJl1QGtr64uDBw92amtrv9d/P6frS7oOr5KT0lJLj+WbjCtTtao4jjN14cKFzqBBg/7dfF6/0bXVnJ+tYeZYbWrXhydNmuSfh+X/6WO6Trbx3HTq1KlnRo0a5Z+Hv9P1iK6TLGPulmaN6BwWs29W6dbQ+1vargN13aTrJ6ZN49ynymYdoOtWXb8wzjj3qfI9huPep3K9EVab+lW5tO0Qc7+ve6NfdSTiF/02QT1zyGloaLC2s2/KYF0/jTg+zpj72FD6mU5QmFM+kGMsD+rjTafBxmN5cRUF9YnXXHPNNxmcX1r0ec0lpJ+zqF2nmNAaNJ63MMBm6pNcMp9lG0qz74roHBazb1bp1tD7W9iuNvWpsllt6lPlewyrmPepLnsjrLb0q3Jp24mmP9Er/app5oW+1bVO11pTl5sPktw2jqCeVgbV1dUdtbiz7xf5tsiZNm3aP//iF79wdBmp/16j62xdzxr3HkusG8Rz5513fvzKK6/4H1T5Bu1oDDtGeQV1XW7Xf/3c4mP5ZXE1NzfbPoWrxu8Erl69Wtr1v5h/l3P4x6Ztt1v8ZZP/O/jYhLq7baJK+61Zsyb1PPyYadP3LHImxDR48OB/3bZtm29V5suIU6bjOyzOfQdd21P7Dhk6h8Xum1WyNeP9LWzXVnP7B6aNa2LYp8rVusHcfjLlWI1bnyrfYzj1cZ/bcBxHWF8296mz/Fx8uV9l/s+9ttz9qp+lvHjof5jKm3pFUO/+7Yv7zcqMGTNsD+quU5c7Qg7eScbdaYn1c2OdGbAOMM4Ltgb1hQsX/ta0o63HsoxSOPv27bM9qC8Q5/z5898L+bzeatr2a8uDeotxNlnWtvLFg/P++++nWmstPDedNOfhhpBj+G7j3Rr3voNKGS3P0Dksdt+skq0Z729hu/r3CxuBi0OfKh+rH1RHBp4jLn2qfI/h1HI0hn2qUG+E9Yy5z0TLz8ULzO1vhjxPWfpVb5kXCRt56BPx5qo5qIvvtN+RsDyoZ+oMp/4uLlhuvVZ1TW+xrl0TiYR//C6x9Fh2r6OS63qrYFGUdhNyllfpYje3mvPRcQupnSFBvUZ1jbraUi6YY3hkhpENJ8bt6/YdTMdPZekcFrtvVsnWjPe3sF1zea4Lllvj0qcq1PpUTPtUod4MVv/69PNVcC72R93n9Nab/da8gSsi/tPMpxNQDUF9fmoHsYqD+hjVNYXLVqtcY3TMOB+1rV11Z9j9j2TdunWvx7BzlGtxr6NavHjxW/X19c6QIUP8RW3k22AZkaq1yPoHE3L++tFHH3VuvfXW0+Yc/pXyRiH7WH5ukgAnI8+jLTwNPy9tK+uipEx9X6viPcIcVi6q6CmIcZ7FNT+ks5jJWuy+WSVbM97fwnaNKnHoU/XUGqc+VSHW+8z9XrLlOM5g9a9PP6zrE7r+MWb9qnza9g8p5+I1qmtxz7L1qy5kOYguqPy+3au6Vd+rOKj7q90/ZJv12LFjTmDhpicsbNYhsiq4rOavy1iLg/rLKnrBk+MWhXV34ZqUnSiC9QMVv9Wiczo36bJGWXgNfmrZt2/f7j59+gQXkttiGVM6QdKeCyKmIF60xBrVOSx236ySrRnvb2G7RpU49qlytV5hPrdx7lNls8r19zIF+pOU8Bb74ziD1bZ+VVTb+gsC7u6tflW2g+hSnv8pEtSrI6j7IzmtNloPHDjgjBs3ThaP+NB8BqRutogpJ9CTMh1crCntauOxLN/wXtId/0b5AsZYZWQu9Zv9Fkus7nXMAwcO/Pbxxx+XsDPK/LtcQ/Y7Y33Kts+rTAcfOnToWfN/1Q3KzjJvwoQJn4R0EuSabpsWzXOnjY4ZM+azF198MXX2wGLTCa6WoF7svhlBvbKDelz7VLlaZbbAH2Lep4qy1ppz8XnVfTV7W4P6GdOGD6eE1Dj3q6La9pLq2qlgecoXEGXrV2X71jbf62UI6vYHdf8/lINV8qWEHNMfKLtG1mVVWef7779vDlitPZYznAxO06cAAAVwSURBVID9xXtOW8J0RyxkdDnEOsVYP7WtXVtaWhxl6ReHprgjyTNnzjwZ+GJtoukcin2WJdbalPNtsO5R8b4uMp/OYbH7ZgT1yrXGuU9VyJcSce1TRVn9c1PCtuO4gHUW4tivimpbfybIopDHlaVf5W/zETZsf4XKf6EagrrF1vb29p8b674q+VLCL8OVXQvKOTlW29vV/13YMkLXqbIvxHXRtnadMGGCf7zatp+4Xz417XpPSLuOM/aPLfL2aWtr23Xdddf5lyCJvymlT2LLl01RncNi980I6pVp3RTzPlWh0/zj2KfKZQaMTX2qQoN6HPtVUW3rr95fE/K4svSr3jQvMi3ktrtU/nsdEtQtLLIf88yZM31nSzW0q+Ur3BPUu59kbRmhe9sEuvFVYPXPTVPlx4gRIz63+LR0UWVfMftiFXxe5yi7ZnNFdQ6L3TcjqFeWVVY+P2xBn8rmFe4J6oUF9Tj2NaLa9m1z+8Desm4xL9Iccluzyn9xHoK6fWXy4MGD//Wqq65yt32y2PmVCTk/ipg2fNrGY9jyqe/nTLveHbEv81uWWN3Rmd///vd/H2L1V6N9z6bG7ezslKmTzrPPPru/Cs5N40LadaSK90romawzQ6w7jHVpFQT1YvfNCOqVY52svJFkmTUxx+Jj+Ctz+7iQx8WxT1XIlxK2Tn339yAfHvK4OParotrWn/WyLuRxZelXTUr5T77OfDtQY/7sD/ffRVCv2qA+TD6QEtRfe+012/dldrc/mj59+kcBqxz/nyoLt2irkqDudu5nz559IqVda8y5z18I5D6LPq8X+vTp8/+ee+45fyEu/zzvL0S2xKbGXb58+a9NsGu0+Ny03T+Gd+7cmdqusm/8CdOuL1tidVfWnTZt2j+3t7f7n9fBytsWR/okZ1T4FETbQk6x+2YE9cqwDjMhR4L6SMuP4efN7ScC1rj2qQjqgX6V8kab/baNc78q22dWZn58p7xt3Wp6o191XGWepnEkz+ciqNtVDqjqmSI9QHUtzBRWD9p6DFse1Acps+VThrrZMu/iCOsh245hs9q7hNf7Lf7vRo7h0xHtKiNztuwdf4MJMWFOCTjjLWrXbB3/YvbNCOqVYbWtTxVlta1PRVC3t1+VrW17vV/VT3mrTso1UfJNrVzrJt92bVD57w1HULerXFDVdS1zn46OjheGDx/uL2J03nSWltt8DFfBqu8DZCHEYcOGOTU1NZdMu8pUpfk2tqsOrfNmzJjhyPZ7KefzR220ms9p6iiztWG9tbX1RTmGjVna9QvljaSPscx6w/r161+Ty63M51WCu4y032TbRzVL57CYfTOCemVYbetTZWtX2U+8xRy3F2PepyKoB/pVypsWLl8ix71flUvbygj6EeOMdb+q6oK65dPBsWLFihUrVqxYsWLFihVvzAtBHStWrFixYsWKFStWrFix4iWo06BYsWLFihUrVqxYsWLFihUvQZ0PK1asWLFixYoVK1asWLHiJajToFixYsWKFStWrFixYsWKFS9BnQ8rVqxYsWLFihUrVqxYseIlqNOgWLFixYoVK1asWLFixYoVL0GdBsWKFStWrFixYsWKFStWgjpBnQbFihUrVqxYsWLFihUrVqx4Ceo0KFasWLFixYoVK1asWLES1AnqNChWrFixYsWKFStWrFixYsVLUKdBsWLFihUrVqxYsWLFihUrQZ0GxYoVK1asWLFixYoVK1aseAnqNChWrFixYsWKFStWrFixYsVLUMeKFStWrFixYsWKFStWrHgJ6jQoVqxYsWLFihUrVqxYsWLFS1Dnw4oVK1asWLFixYoVK1aseAnqNChWrFixYsWKFStWrFixYq0g7/8HKEp8nC5bo8EAAAAASUVORK5CYIJXcVV+robTcIqtuIqruHLlylVcxVVcxZYrV67i6iDEVWy5iqu4iqu4iitXcRVbcRVX5edqOA2n2IqruIorV65cxVVcxVVsuXLlKq4OQlzFlqu4iqu4iqu4chVXsRVXcVV+robTcIqtuIqruHLlylVcxVVcxZYrV67i6iDEVWy5iqu4iqu4iitXcRVbcRVX5edqOA2n2IqruIorV65cxVVcxVVsuXLlKq4OQlzFlqu4iqu4iqu4chVXsRVXcVVy1/8LP/ekHAAOxXoAAAAASUVORK5CYIL1h3e2ju7Z1jr+o++2psbTPhN/Do6ldxxEe2MBvQJ6Bb0CWDygV0CvgGZBr4BeAb1C8Q6Op1/OHc6aMsdBtDcW0CugV9ArgMUDegX0CmgW9AroFdArFOvgWDrgaLj4OeSfdG8soFdAr6BXAIsH9AroFdAs6BXQK6BXKNLBL6TvzR3OHt2zrTU1nvaZsubQRPqMf9K9sYBeAb2CXgEsHtAroFdAs6BXQK+AXqFIB7enR+YOok/85BHNgjcW0CvoFdArgMUDegX0CmgW9AroFdArxOEgGryxgF5Br3oFvQJYPKBXQK+AZkGvgF4BvUJYDqLBGwvoFfSqV9ArgMUDegX0CmgW9AroFdArhOUgGryxgF5Br3oFvQJYPKBXQK+AZkGvgF4BvUJYDqLBGwvoFfSqV9ArgMUDegX0CmgW9AroFdArhOUgGryxgF5Br3oFvQJYPKBXQK+AZkGvgF4BvUJYDqLBGwvoFfSqV9ArgMUDegX0CmgW9AroFdArhOUgGryxgF5Br3oFvQJYPKBXQK+AZkGvgF4BvUJYDqLBGwvoFfSqV9ArgMUDegX0CmgW9AroFdArhOUgGryxgF5Br3oFvQJYPKBXQK+AZkGvgF4BvUJYDqLBGwvoFfSqV9ArgMUDegX0CmgW9AroFfgPO3cYWvd53n38nmYXLwRTkYkmhIy+KHlRijGSPI91xgl1sjQbJSsUs2UwQ9thTDB9MbZACPOLhYXWlI51iyU3Vs0GbqGYTGPrRjBpX4RhCCaYsY5B8EwwxQzakhnPeIaz+8xSqvOXnPwlH8nn9z+fD1z06TMdPQfP3+t+8VxYrxDLQTR4YwG9gl71CnoFsHhAr4BeAc2CXgG9AnqFWA6iwRsL6BX0qlfQK4DFA3oF9ApoFvQK6BXQK8RyEA3eWECvoFe9gl4BLB7QK6BXQLOgV0CvgF4hloNo8MYCegW96hX0CmDxgF4BvQKaBb0CegX0CrEcRIM3FtAr6FWvoFcAiwf0CugV0CzoFdAroFeI5SAavLGAXkGvegW9Alg8oFdAr4BmQa+AXgG9QiwH0eCNBfQKetUr6BXA4gG9AnoFNAt6BfQK6BViOYgGbyygV9CrXkGvABYP6BXQK6BZ0CugV0CvEMtBNHhjAb2CXvUKegWweECvgF4BzYJeAb0CeoVYDqLBGwvoFfSqV9ArgMUDegX0CmgW9AroFdArxHIQDd5YQK+gV72CXgEsHtAroFdAs6BXQK+AXiGWg2jwxgJ6Bb3qFfQKYPGAXgG9ApoFvQJ6BfQKsRxEgzcW0CvoVa+gVwCLB/QK6BXQLOgV0CugV4jlIBq8sYBeQa96Bb0CWDygV0CvgGZBr4BeAb1CLAfR4I0F9Ap61SvoFcDiAb0CegU0C3oF9AroFWI5iAZvLKBX0KteQa8AFg/oFdAroFnQK6BXQK8Qy0E0eGMBvYJe9Qp6BbB4QK+AXgHNgl4BvQJ6hVgOosEbC+gV9KpX0CuAxQN6BfQKaBb0CugV0CvEchAN3lhAr6BXvYJeASwe0CugV0CzoFdAr4BeIZaDaPDGAnoFveoV9Apg8YBeAb0CmgW9AnoF9AqxHESDNxbQK+hVr6BXAIsH9AroFdAs6BXQK6BXiOUgGryxgF5Br3oFvQJYPKBXQK+AZkGvgF4BvUIsB9HgjQX0CnrVK+gVwOIBvQJ6BTQLegX0CugVYjmIBm8soFfQq15BrwAWD+gV0CugWdAroFdArxDLQTR4YwG9gl71CnoFsHhAr4BeAc2CXgG9AnqFWA6iwRsL6BX0qlfQK4DFA3oF9ApoFvQK6BXQK8RyEA3eWECvoFe9gl4BLB7QK6BXQLOgV0CvgF4hloNo8MYCegW96hX0CmDxgF4BvQKaBb0CegX0CrEcRIM3FtAr6FWvoFcAiwf0CugV0CzoFdAroFeI5SAavLGAXkGvegW9Alg8oFdAr4BmQa+AXgG9QiwH0eCNBfQKetUr6BXA4gG9AnoFNAt6BfQK6BViOYgGbyygV9CrXkGvABYP6BXQK6BZ0CugV0CvEMtBNHhjAb2CXvUKegWweECvgF4BzYJeAb0CeoVYDqLBGwvoFfSqV9ArgMUDegX0CmgW9AroFdArxHIQDd5YQK+gV72CXgEsHtAroFdAs6BXQK+AXiGWg2jwxgJ6Bb3qFfQKYPGAXgG9ApoFvQJ6BfQKsRxEgzcW0CvoVa+gVwCLB/QK6BXQLOgV0CugV4jlIBq8sYBeQa96Bb0CWDygV0CvgGZBr4BeAb1CLAfR4I0F9Ap61SvoFcDiAb0CegU0C3oF9AroFWI5iAZvLKBX0KteQa8AFg/oFdAroFnQK6BXQK8Qy0E0eGMBvYJe9Qp6BbB4QK+AXgHNgl4BvQJ6hVgOosEbC+gV9KpX0CuAxQN6BfQKaBb0CugV0CvEchAN3lhAr6BXvYJeASwe0CugV0CzoFdAr4BeIZaDaPDGAnoFveoV9Apg8YBeAb0CmgW9AnoF9AqxHESDNxbQK+hVr6BXAIsH9AroFdAs6BXQK6BXiOUgGryxgF5Br3oFvQJYPKBXQK+AZkGvgF4BvUIsB9HgjQX0CnrVK+gVwOIBvQJ6BTQLegX0CugVYjmIBm8soFfQq15BrwAWD+gV0CugWdAroFdArxDLQTR4YwG9gl71CnoFsHhAr4BeAc2CXgG9AnqFWA6iwRsL6BX0qlfQK4DFA3oF9ApoFvQK6BXQK8RyEA3eWECvoFe9gl4BLB7QK6BXQLOgV0CvgF4hloNo8MYCegW96hX0CmDxgF4BvQKaBb0CegX0CrEcRIM3FtAr6FWvoFcAiwf0CugV0CzoFdAroNexMDdT/nz5cNZ0cxxEgzcW0CvoFdArgMUDegX0CmgW9AroFdBrZ83Nlh84GnYQDXhjAb2CXgG9AhYPoFdAr6BZQK+AXkGvRJrbU769fDg7P1N+Wv/zkunGnHriwV5//vHVb2gWvLGAXkGvgF4BLB7QK6BXQLOgV0CvgF67aW62HHv/XxOu/2d/IpoF9AroFfQK6BWweAC9AnoFzQJ6BfQKeiWGg2jNAnoF9Ap6BfQKWDyAXgG9gmYBvQJ6Bb0Sy0G0ZgG9AnoFvQJ6BSweQK+AXkGzgF4BvYJeieUgWrOAXgG9gl4BvQIWD6BXQK+gWUCvgF5Br8RyEK1ZQK+AXkGvgF4BiwfQK6BX0CygV0CvoFdiOYjWLKBXQK+gV0CvgMUD6BXQK2gW0CugV9ArsRxEaxbQK6BX0CugV8DiAfQK6BU0C+gV0CvolVgOojUL6BXQK+gV0Ctg8QB6BfQKmgX0CugV9EosB9GaBfQK6BX0CugVsHgAvQJ6Bc0CegX0CnolloNozQJ6BfQKegX0Clg8gF4BvYJmAb0CegW9EstBtGYBvQJ6Bb0CegUsHkCvgF5Bs4BeAb2CXonlIFqzgF4BvYJeAb0CFg+gV0CvoFlAr4BeQa/EchCtWUCvgF5Br4BeAYsH0CugV9AsoFdAr6BXYjmI1iygV0CvoFdAr4DFA+gV0CtoFtAroFfQK7EcRGsW0CugV9AroFfA4gH0CugVNAvoFdAr6JVYDqI1C+gV0CvoFdArYPEAegX0CpoF9AroFfRKLAfRmgX0CugV9AroFbB4AL0CegXNAnoF9Ap6JZaDaM0CegX0CnoF9ApYPIBeAb2CZgG9AnoFvRLLQbRmAb0CegW9AnoFLB5Ar4BeQbOAXgG9gl6J5SBas4BeAb2CXgG9AhYPoFdAr6BZQK+AXkGvxHIQrVlAr4BeQa+AXgGLB9AroFfQLKBXQK+gV2I5iNYsoFdAr6BXQK+AxQPoFdAraBbQK6BX0CuxHERrFtAroFfQK6BXwOIB9AroFTQL6BXQK+iVWA6iNQvoFdAr6BXQK2DxAHoF9AqaBfQK6BX0SiwH0ZoF9AroFfQK6BWweAC9AnoFzQJ6BfQKeiWWg2jNAnoF9Ap6BfQKWDyAXgG9gmYBvQJ6Bb0Sy0G0ZgG9AnoFvQJ6BSweQK+AXkGzgF4BvYJeieUgWrOAXgG9gl4BvQIWD6BXQK+gWUCvgF5Br8RyEK1ZQK+AXkGvgF4BiwfQK6BX0CygV0CvoFdiOYjWLKBXQK+gV0CvgMUD6BXQK2gW0CugV9ArsRxEaxbQK6BX0CugV8DiAfQK6BU0C+gV0CvolVgOojUL6BXQK+gV0Ctg8QB6BfQKmgX0CugV9EosB9GaBfQK6BX0CugVsHgAvQJ6Bc0CegX0CnolloNozQJ6BfQKegX0Clg8gF4BvYJmAb0CegW9EstBtGYBvQJ6Bb0CegUsHkCvgF5Bs4BeAb2CXonlIFqzgF4BvYJeAb0CFg+gV0CvoFlAr4BeQa/EchCtWUCvgF5Br4BeAYsH0CugV9AsoFdAr6BXYjmI1iygV0CvoFdAr4DFA+gV0CtoFtAroFfQK7EcRGsW0CugV9AroFfA4gH0CugVNAvoFdAr6JVYDqI1C+gV0CvoFdArYPEAegX0CpoF9AroFfRKLAfRmgX0CugV9AroFbB4AL0CegXNAnoF9Ap6JZaDaM0CegX0CnoF9ApYPIBeAb2CZgG9AnoFvRLLQbRmAb0CegW9AnoFLB5Ar4BeQbOAXgG9gl6J5SBas4BeAb2CXgG9AhYPoFdAr6BZQK+AXkGvxHIQrVlAr4BeQa+AXgGLB9AroFfQLKBXQK+gV2I5iNYsoFdAr6BXQK+AxQPoFdAraBbQK6BX0CuxHERrFtAroFfQK6BXwOIB9AroFTQL6BXQK+iVWA6iNQvoFdAr6BXQK2DxAHoF9AqaBfQK6BX0SiwH0ZoF9AroFfQK6BWweAC9AnoFzQJ6BfQKeiWWg2jNAnoF9Ap6BfQKWDyAXgG9gmYBvQJ6Bb0Sy0G0ZgG9AnoFvQJ6BSweQK+AXkGzgF4BvYJeieUgWrOAXgG9gl4BvQIWD6BXQK+gWUCvgF5Br8RyEK1ZQK+AXkGvgF4BiwfQK6BX0CygV0CvoFdiOYjWLKBXQK+gV0CvgMUD6BXQK2gW0CugV9ArsRxEaxbQK6BX0CugV8DiAfQK6BU0C+gV0CvolVgOojUL6BXQK+gV0Ctg8QB6BfQKmgX0CugVxsL3T/1l728O7u797e/N9g9n/+z/D2lN/iwfQzuI9sYCegX0CnoF9ApYPIBeAb2CZgG9AnqFLlv47CO9geNZ071xEO2NBfQK6BX0CugVsHgAvQJ6Bc0CegX0Cl218JSD6DGY5/1N98YCegX0CnoF9ApYPIBeAb2CZgG9AnqFTjrzpc+8fzg7P1O+NT9dDpnuzInp8vsLj5Ud/qZ7YwG9AnoFvQJ6BSweQK+AXkGzgF4BvUInnTn81M8PoqfLIX8i4I0F9Ap6BfQK6BWweAC9AnoFzQJ6Bb3qFWI4iAZvLKBX0KteQa+AXgGLB9AroFfQLKBXQK8Qy0E0eGMBvYJe9Qp6BfQKWDyAXgG9gmYBvQJ6hVgOosEbC+gV9KpX0CugV8DiAfQK6BU0C+gV0CvEchAN3lhAr6BXvYJeAb0CFg+gV0CvoFlAr4BeIZaDaPDGAnoFveoV9AroFbB4AL0CegXNAnoF9AqxHESDNxbQK+hVr6BXQK9w254636zzdp3rdW4u/ef5Ol+vsyv8e+xb+vy5Oj+rc2Ppd79X5606J+s8afEAegX0CpoF9AroFdI4iAZvLKBX0KteQa+AXhl3D9R5rU6vxZytMxX2PT5dbh9X91rOv9V53OIB9AroFTQL6BX0qldI4SAavLGAXkGvegW9AnplnO0s6zsW7s87ZfhH0Zv1PZ5b5+9cOUctHkCvoFe9gmYBvYJe9QoJHESDNxbQK+hVr6BXQK+Ms4WysWPhMwHf42DZ+DH08jxr8QB6Bb3qFTQL6BX0qlcYdQ6iwRsL6BX0qlfQK6BXxtWusvoA+Eqdw3Uml35mcum/X13jZx8d4e9xX53/avzcrTqv1vlcuf0vUpcVv7t/PP3mGr/7Z3UesHgAvYJe/WmAZgG9gl6BUeYgGryxgF5Br3oFvQJ6ZVydLIPHvxfqTN3hZx+q827j5786wt/jcONn+ofUe1p8lz8pq4+iX7R4AL2CXv1pgGYBvYJegVHmIBq8sYBeQa96Bb0CemUcTdR5rwwe/n7yQz6zv/Hzl0f4eyw2fubZdXynucZn37R4AL2CXv1pgGYBvYJegVHmIBq8sYBeQa96Bb0CemUc7Sur/1XmNi42PvepEf0ezSPriXV8p0cbn71u8QB6Bb360wDNAnoFvQKjzEE0eGMBvYJe9Qp6BfTKOHquDB79Hm/5ueONzx3pyPdoWvm7b1o8gF5Br/40QLOAXkGvwChzEA3eWECvoFe9gl4BvTKOTpfBo98vtPzcwcbnTnfke6z0kcbvfs/iAfQKevWnAZoF9Ap6BUaZg2jwxgJ6Bb3qFfQK6JVxtFgGj34PtPzcgcbnFjvyPVb63cbv/p7FA+gV9OpPAzQL6BX0CowyB9HgjQX0CnrVK+gV0Cvj6FIZPPqdbPm5nY3P/bgj32OlC43f/YcWD6BX0Ks/DdAsoFfQKzDKHESDNxbQK+hVr6BXQK/c878oWz07duxYefDbO3fuXKvP9X9u5ef6v6cL32N5Dh06NPB7p6ameq+//nrvXv7vyhhjjDHGGGOMMcYYY4z5sFl5EL34tef9mRhjjDHGGGOMMcYYY7Zk7ulB9LZt2wYOf9f1xVd8bvv27Z34Hv154YUXBn5nf44dO+YvqzHGGGOMMcYYY4wxxhgH0cYYY4wxxhhjjDHGGDNqB9HNw9+NfnZiYqIT32OtY+inn37aX1RjjDHGGGOMMcYYY4wxDqKNMcYYY4wxxhhjjDHmzve891TzAHijn73Zge9xdI3v8Uadj5Qgo/SXC9Ar6BXQLKBX0CuwtVYeRM9Pl0P+RMAbC+gV9AroFdAr4+BGGc4h8o3w7/FSWX0M/Wad+y0eQK+AXkGzgF5Br3qFFA6iwRsL6BX0qlfQK6BXxtG1MngEPNHyc9san7sW+j36//rzmbL6GPqfSuAxtMUDegX0CmgW9AroFcabg2jwxgJ6Bb3qFfQK6JVx9E4ZPAS+r+XndjY+dyXwe0yV2/8KdPMY+my5fWht8QB6BfQKmgX0CugVojiIBm8soFfQq15Br4BeGUeLZfAY+EDLz+1vfG4x7Ht8us67ZfUx9HGLB9AroFfQLKBXQK+QykE0eGMBvYJe9Qp6BfTKODpdBg+Cn2n5uc83Pnc66HscrXOr8bmbdf7A4gH0CugVNAvoFdArJHMQDd5YQK+gV72CXgG9Mo6+WAYPg19u+bmXGp87GvI9TpbV/yr05Tp7LB5Ar4BeQbOAXgG9QjoH0eCNBfQKetUr6BXQK+Oofwi88jj4fMvPvdX43OMB32OhrD6GPldnyuIB9AroFTQL6BXQK3SBg2jwxgJ6Bb3qFfQK6JVx9ZMyeCS890N+fm/j56/VmRjx7/FiWX0M/XIX/5dp8YBeAb2CZjULegX0CuPLQTR4YwG9gl71CnoF9Mq4miuDh8KX6jx0h599uM7lxs+/OuLfY3fj527WOWjxAHoF9AqaBfQK6BW6xkE0eGMBvYJe9Qp6BfTKuGoeDPfnap0jdSaXfmZq6b9fXeNnd4349zjf+LlnLB5Ar4BeQbOAXgG9Qhc5iAZvLKBX0KteQa+AXhlnr5XVB8ZtZqHF725+Ziu/x/4N/r47jcUD6BX0CmgW0CvoFRhZDqLBGwvoFfSqV9AroFfG2SN1rpT1HQdfrLOzxe9ez1HxsL/HQnEQDegV0CtoFtAroFcYEw6iwRsL6BX0qlfQK6BXxt3H6rxR2h0G9/8l58mWv3e9R8XD/B6XioNoQK+AXkGzgF4BvcKYcBAN3lhAr6BXvYJeAb3CbfvqzNV5u871OreW/vPC0v/93nX+vo0eFQ/je9wqDqIBvQJ6Bc0CegX0CmPCQTR4YwG9gl71CnoF9ApYPIBeAb2CZgG9AnqFWA6iwRsL6BX0qlfQK6BXwOIB9AroFTQL6BXQK8RyEA3eWECvoFe9gl4BvQIWD6BXQK+gWUCvgF4hloNo8MYCegW96hX0CugVsHgAvQJ6Bc0CegX0CrEcRIM3FtAr6FWvoFdAr4DFA+gV0CtoFtAroFeI5SAavLGAXkGvegW9AnoFLB5Ar4BeQbOAXgG9QiwH0eCNBfQKetUr6BXQK2DxAHoF9AqaBfQK6BViOYgGbyygV9CrXkGvgF4BiwfQK6BX0CygV0CvEMtBNHhjAb2CXvUKegX0Clg8gF4BvYJmAb0CeoVYDqLBGwvoFfSqV9AroFfA4gH0CugVNAvoFdArxHIQDd5YQK+gV72CXgG9AhYPoFdAr6BZQK+AXiGWg2jwxgJ6Bb3qFfQK6BWweAC9AnoFzQJ6BfQ6FhYeKx/969nylbmZ8qVXZstjphtz6okHHUSDNxbQK+hVr6BXQK+AxQPoFdAraBbQK6DX7pubLpeXD2dNN8dBNHhjAb2CXgG9AnoFLB5Ar4BeQbOAXgG9dtb8TPmpo2EH0YA3FtAr6BXQK6BXwOIB9Ap6BTQL6BX0SqS5mXJh+XD2xGz5/omZsmDy58zhp3r9+e7R3+kt7C4f9TcdvLGAXkGvgF4BvQIWD6BXQK+gWUCvoFe9dtL8THlj+SD6ldnymD8RvQKaBfQKegX0CugVsHgAvYJeAc0CegW9EsNBtF4BzQJ6Bb0CegX0Clg8gF5Br4BmAb2CXonlIFqvgGYBvYJeAb0CegUsHkCvoFdAs4BeQa/EchCtV0CzgF5Br4BeAb0CFg+gV9AroFlAr6BXYjmI1iugWUCvoFdAr4BeAYsH0CvoFdAsoFfQK7EcROsV0CygV9AroFdAr4DFA+gV9ApoFtAr6JVYDqL1CmgW0CvoFdAroFfA4gH0CnoFNAvoFfRKLAfRegU0C+gV9AroFdArYPEAegW9ApoF9Ap6JZaDaL0CmgX0CnoF9AroFbB4AL2CXgHNAnoFvRLLQbReAc0CegW9AnoF9ApYPIBeQa+AZgG9gl6J5SBar4BmAb2CXgG9AnoFLB5Ar6BXQLOAXkGvxHIQrVdAs4BeQa+AXgG9AhYPoFfQK6BZQK+gV2I5iNYroFlAr6BXQK+AXgGLB9Ar6BXQLKBX0CuxHETrFdAsoFfQK6BXQK+AxQPoFfQKaBbQK+iVWA6i9QpoFtAr6BXQK6BXwOIB9Ap6BTQL6BX0SiwH0XoFNAvoFfQK6BXQK2DxAHoFvQKaBfQKeiWWg2i9ApoF9Ap6BfQK6BWweAC9gl4BzQJ6Bb0Sy0G0XgHNAnoFvQJ6BfQKWDyAXkGvgGYBvYJeieUgWq+AZgG9gl4BvQJ6BSweQK+gV0CzgF5Br8RyEK1XQLOAXkGvgF4BvQIWD6BX0CugWUCvoFdiOYjWK6BZQK+gV0CvgF4BiwfQK+gV0CygV9ArsRxE6xXQLKBX0CugV0CvgMUD6BX0CmgW0CvolVgOovUKaBbQK+gV0CugV8DiAfQKegU0C+gV9EosB9F6BTQL6BX0CugV0Ctg8QB6Bb0CmgX0CnolloNovQKaBfQKegX0CugVsHgAvYJeAc0CegW9EstBtF4BzQJ6Bb0CegX0Clg8gF5Br4BmAb2CXonlIFqvgGYBvYJeAb0CegUsHkCvoFdAs4BeQa/EchCtV0CzgF5Br4BeAb0CFg+gV9AroFlAr6BXYjmI1iugWUCvoFdAr4BeAYsH0CvoFdAsoFfQK7EcROsV0CygV9AroFdAr4DFA+gV9ApoFtAr6JVYDqL1CmgW0CvoFdAroFfA4gH0CnoFNAvoFfRKLAfRegU0C+gV9AroFdArYPEAegW9ApoF9Ap6JZaDaL0CmgX0CnoF9AroFbB4AL2CXgHNAnoFvRLLQbReAc0CegW9AnoF9ApYPIBeQa+AZgG9gl6J5SBar4BmAb2CXgG9AnoFLB5Ar6BXQLOAXkGvxHIQrVdAs4BeQa+AXgG9AhYPoFfQK6BZQK+gV2I5iNYroFlAr6BXQK+AXgGLB9Ar6BXQLKBX0CuxHETrFdAsoFfQK6BXQK+AxQPoFfQKaBbQK+iVWA6i9QpoFtAr6BXQK6BXwOIB9Ap6BTQL6BX0SiwH0XoFNAvoFfQK6BXQK2DxAHoFvQKaBfQKeiWWg2i9ApoF9Ap6BfQK6BWweAC9gl4BzQJ6Bb0Sy0G0XgHNAnoFvQJ6BfQKWDyAXkGvgGYBvcJY+N4fP9s79ZsP9779uU/0TsyW0ydmyoLJn+VjaAfR3ldAs4BeQa+AXgG9AhYPoFfQK6BZQK/QafO/+ou9lcezpnvjINr7CmgW0CvoFdAroFfA4gH0CnoFNAvoFTprfu92R8Mdn5PT5df8Tfe+ApoF9Ap6BfQK6BWweAC9gl4BzQJ6hU469Zmp9w9n52fKH81Pl0OmU/Pb/pZ7XwHNAnoFvQJ6BfQKWDyAXkGvgGYBvUJnnXriwfcPol/ZXT7uTwS8r4BmQa+AXgG9gl4BLB5Ar6BXQLOgV71CDAfR4H0FNAt61SvoFdAr6FWvgMUD6BX0CmgW0CvEchAN3ldAs6BXvYJeAb2CXvUKWDyAXkGvgGYBvUIsB9HgfQU0C3rVK+gV0CvoVa+AxQPoFfQKaBbQK8RyEA3eV0CzoFe9gl4BvYJe9QpYPIBeQa+AZgG9QiwH0eB9BTQLetUr6BXQK+hVr4DFA+gV9ApoFtArxHIQDd5XQLOgV72CXgG9gl71Clg8gF5Br4BmAb1CLAfR4H0FNAt61SvoFdAr6FWvgMUD6BX0CmgW0CvEchAN3ldAs6BXvYJeAb2CXvUKWDyAXkGvgGYBvUIsB9HgfQU0C3rVK+gV0CvoVa+AxQPoFfQKaBbQK8RyEA3eV0CzoFe9gl4BvYJe9QpYPIBeQa+AZgG9QiwH0eB9BTQLetUr6BXQK+hVr4DFA+gV9ApoFtArxHIQDd5XQLOgV72CXgG9gl71Clg8gF5Br4BmAb1CLAfR4H0FNAt61SvoFdAr6FWvgMUD6BX0CmgW0CvEchAN3ldAs6BXvYJeAb2CXvUKWDyAXkGvgGYBvUIsB9HgfQU0C3rVK+gV0CvoVa+AxQPoFfQKaBbQK8RyEA3eV0CzoFe9gl4BvYJe9QpYPIBeQa+AZgG9QiwH0eB9BTQLetUr6BXQK+hVr4DFA+gV9ApoFtArxHIQDd5XQLOgV72CXgG9gl71Clg8gF5Br4BmAb1CLAfR4H0FNAt61SvoFdAr6FWvgMUD6BX0CmgW0CvEchAN3ldAs6BXvYJeAb2CXvUKWDyAXkGvgGYBvUIsB9HgfQU0C3rVK+gV0CvoVa+AxQPoFfQKaBbQK8RyEA3eV0CzoFe9gl4BvYJe9QpYPIBeQa+AZgG9QiwH0eB9BTQLetUr6BXQK+hVr4DFA+gV9ApoFtArxHIQDd5XQLOgV72CXgG9gl71Clg8gF5Br4BmAb1CLAfR4H0FNAt61SvoFdAr6FWvgMUD6BX0CmgW0CvEchAN3ldAs6BXvYJeAb2CXvUKWDyAXkGvgGYBvUIsB9HgfQU0C3rVK+gV0CvoVa+AxQPoFfQKaBbQK8RyEA3eV0CzoFe9gl4BvYJe9QpYPIBeQa+AZgG9QiwH0eB9BTQLetUr6BXQK+hVr4DFA+gV9ApoFtArxHIQDd5XQLOgV72CXgG9gl71Clg8gF5Br4BmAb1CLAfR4H0FNAt61SvoFdAr6FWvgMUD6BX0CmgW0CvEchAN3ldAs6BXvYJeAb2CXvUKWDyAXkGvgGYBvUIsB9HgfQU0C3rVK+gV0CvoVa+AxQPoFfQKaBbQK8RyEA3eV0CzoFe9gl4BvYJe9QpYPIBeQa+AZgG9QiwH0eB9BTQLetUr6BXQK+hVr4DFA+gV9ApoFtDrWDgxU/5lbrb879xM+e86l0xnxkE0eF8BzYJe9Qp6BfQKetUrYPEAegW9ApoF9Np9S8fQPdPdcRAN3ldAs6BXQK+AXkGvABYPoFfQK6BZQK+dNT9T/sfRcHfn5G/c3//PX/Y3HbyvgGZBr4BeAb2CXgEsHkCvoFdAs6BXvXbS/Ez5z5X/krDpxrx+9ju9/pz7h7/TK3hfAc2CXgG9AnoFvQJYPIBeQa+AZgG9dtfcTLm0fBDtT0OvgF4BzYJeAb0CegW9Alg8oFdAr4BmQa9EcRCtV0CvgGZBr4BeAb2CXgEsHtAroFdAs6BXYjmI1iugV0CzoFdAr4BeQa8AFg/oFdAroFnQK7EcROsV0CugWdAroFdAr6BXAIsH9AroFdAs6JVYDqL1CugV0CzoFdAroFfQK4DFA3oF9ApoFvRKLAfRegX0CmgW9AroFdAr6BXA4gG9AnoFNAt6JZaDaL0CegU0C3oF9AroFfQKYPGAXgG9ApoFvRLLQbReAb0CmgW9AnoF9Ap6BbB4QK+AXgHNgl6J5SBar4BeAc2CXgG9AnoFvQJYPKBXQK+AZkGvxHIQrVdAr4BmQa+AXgG9gl4BLB7QK6BXQLOgV2I5iNYroFdAs6BXQK+AXkGvABYP6BXQK6BZ0CuxHETrFdAroFnQK6BXQK+gVwCLB/QK6BXQLOiVWA6i9QroFdAs6BXQK6BX0CuAxQN6BfQKaBb0SiwH0XoF9ApoFvQK6BXQK+gVwOIBvQJ6BTQLeiWWg2i9AnoFNAt6BfQK6BX0CmDxgF4BvQKaBb0Sy0G0XgG9ApoFvQJ6BfQKegWweECvgF4BzYJeieUgWq+AXgHNgl4BvQJ6Bb0CWDygV0CvgGZBr8RyEK1XQK+AZkGvgF4BvYJeASwe0CugV0CzoFdiOYjWK6BXQLOgV0CvgF5BrwAWD+gV0CugWdArsRxE6xXQK6BZ0CugV0CvoFcAiwf0CugV0CzolVgOovUK6BXQLOgV0CugV9ArgMUDegX0CmgW9EosB9F6BfQKaBb0CugV0CvoFcDiAb0CegU0C3olloNovQJ6BTQLegX0CugV9Apg8YBeAb0CmgW9EstBtF4BvQKaBb0CegX0CnoFsHhAr4BeAc2CXonlIFqvgF4BzYJeAb0CegW9Alg8oFdAr4BmQa/EchCtV0CvgGZBr4BeAb2CXgEsHtAroFdAs6BXYjmI1iugV0CzoFdAr4BeQa8AFg/oFdAroFnQK7EcROsV0CugWdAroFdAr6BXAIsH9AroFdAs6JVYDqL1CugV0CzoFdAroFfQK4DFA3oF9ApoFvRKLAfRegX0CmgW9AroFdAr6BXA4gG9AnoFNAtj4e//4k973z3yW72zL365Nz9dDpluzPIxtINo7yugV0CzoFdAr4BeQa8AFg/oFdAroFnotLnZX+itPJ413Rt/y72vgF4BzYJeAb0CegW9Alg8oFdAr4BmobMcDDuIxvsK6BU0q1nQK6BX0KteQa8AFg/oFdAroFmItXw0O//rv9Q7MVMWTLdmbrp8xd9y7yugV0CzoFdAr4BeQa8AFg/oFdAroFnorOWD6FNPPKhX8L4CegXNAnoF9Ap6BfQKYPGAXgG9ApqFLA6iwfsK6BU0q1nQK6BX0KteQa8AFg/oFdAroFmI5SAavK+AXkGzmgW9AnoFveoV9Apg8YBeAb0CmoVYDqLB+wroFTSrWdAroFfQq15BrwAWD+gV0CugWYjlIBq8r4BeQbOaBb0CegW96hX0CptlT51v1nm7zvU6N5f+83ydr9fZ1dHvcbFOb2ksHkCvgF5Bs8AmcxAN3ldAr6BZzYJeAb2CXvUKeoVhe6DOa+XnR8EfNGfrTHXoe7zQ+L0WD6BXQK+gWWCTOYgG7yugV9CsZkGvgF5Br3oFvcIw7Sy3/yXm3jrmnTL8o+h78T2eWuN3WjyAXgG9gmaBTeYgGryvgF5Bs5oFvQJ6Bb3qFfQKw7RQ1neEvDxnwr/Hk3WuFwfRgF4BvYJmgS3nIBq8r4BeQbOaBb0CegW96hX0CsOyq6w+CL5S53CdyaWfmVz671fX+NlHQ7/HwTo3ytoH1hYPoFdAr6BZYJM5iAbvK6BX0KxmQa+AXkGvegW9wrCcLIPHwBfqTN3hZx+q827j578a9j121PlG+eB/cdriAfQK6BU0C2wyB9HgfQX0CprVLOgV0CvoVa+gVxiGiTrvlcFj4E9+yGf2N37+ctD3eLLOvzc+t9a/Nm3xAHoF9AqaBTaZg2jwvgJ6Bc1qFvQK6BX0qlfQKwzDvrL6X2Vu42Ljc58K+B4/LKsPn/+jzieKg2hAr4BeQbPAlnMQDd5XQK+gWc2CXgG9gl71CnqFYXiuDB4CH2/5ueONzx0J+B7No+eTde6/w//M4gH0CugVNAtsMgfR4H0F9Aqa1SzoFdAr6FWvoFcYhtNl8BD4Cy0/d7DxudMB32P5Z/613P4Xqdf6nzmIBvQK6BU0C2wRB9HgfQX0CprVLOgV0CvoVa+gVxiGxTJ4CHyg5ecOND63GPA9LtZ59g7/MwfRgF4BvYJmgS3mIBq8r4BeQbOaBb0CegW96hX0CsNwqQweAk+2/NzOxud+HP49HEQDegX0CpoFtpiDaPC+AnoFzWoW9AroFfSqV9ArHfyLstWzY8eOgUPgc+fOtfpc/+dWfq7/e5K/R2kcRN/L/50YY4wxxhhjjDHjMisPov15GGOMMcYYY4wxxhhjjDHGGJM79/Qgetu2bRs+BF75ue3bt0d/DwfRxhhjjDHGGGOMg2hjjDHGGGOMMcYYY4wxxhhjTOBB9N0cAq/83MTERPT3cBBtjDHGGGOMMcY4iDbGGGOMMcYYY4wxxhhjjDHGbPgW+J5qHgNv9LM3w7/H3fy/P1JG6S8XoFfQK6BZ4IOsPIj2pwHeV0CvoFlAr4BeQa+AXmGjbpThHCLfCP8eDqIBvQJ6Bc0CW8xBNHhfAb2CZjULegX0CnrVK+gVhuFaGTwEnmj5uW2Nz10L/x4OogG9AnoFzQJbzEE0eF8BvYJmNQt6BfQKetUr6BWG4Z0yeAh8X8vP7Wx87kr493AQDegV0CtoFthiDqLB+wroFTSrWdAroFfQq15BrzAMi2XwEPhAy8/tb3xuMfx7OIgG9AroFTQLbDEH0eB9BfQKmtUs6BXQK+hVr6BXGIbTZfAQ+JmWn/t843Onw7+Hg2hAr4BeQbPAFnMQDd5XQK+gWc2CXgG9gl71CnqFYfhiGTwEfrnl515qfO5o+PdwEA3oFdAraJYRNj9TvjU3W35Q50SdY6Yj4yAavK+AXkGzmgW9AnoFveoV9ApDsKcMHgKfb/m5txqfezz8eziIBvQK6BU0y4ia31P2LB/Omm6Og2jwvgJ6Bc1qFvQK6BX0CugV7tZPyuAx8N4P+fm9jZ+/Vmci/Hs4iAb0CugVNMuI+qvdDqK7Pguf/RW9gvcV0CtoFtAroFfQK6BXuCtzZfAY+FKdh+7wsw/Xudz4+Vc78D0cRAN6BfQKmmVEvbK7fHz5cHZ+pvxofrocMt2Yxa893+vPP39nQa/gfQX0CpoF9AroFfQK6BXuyu6y+iD4ap0jdSaXfmZq6b9fXeNnd3XgeziIBvQK6BU0y4hqHES/4U9Er4BeAb2CZgG9AnoFvQJ6hbW8VlYfBbeZhRa/ez3Hxpv5PYb1HS0eQK+gV0CzbCEH0XoF9AroFTQL6BXQK+gV0Cu08UidK2V9R8gX6+xs8bvXc2y8md9jWN/R4gH0CnoFNMsWchCtV0CvgF5Bs4BeAb2CXgG9Qlsfq9P//1huc4Tc/5ecJ1v+3vUeG2/W9xjmd7R4AL2CXgHNskUcROsV0CugV9AsoFdAr6BXQK+wXvvqzNV5u871OreW/vPC0v/93nX+vo0eGw/7e2zGd7R4AL2CXgHNsskcROsV0CugV9AsoFdAr6BXQK+AxQPoFdAraJZYDqL1CugV0CtoFtAroFfQK6BXwOIB9AroFTRLLAfRegX0CugVNAvoFdAr6BXQK2DxAHoF9AqaJZaDaL0CegX0CpoF9AroFfQK6BWweAC9AnoFzRLLQbReAb0CegXNAnoF9Ap6BfQKWDyAXgG9gmaJ5SBar4BeAb2CZgG9AnoFvQJ6BSweQK+AXkGzxHIQrVdAr4BeQbOAXgG9gl4BvQIWD6BXQK+gWWI5iNYroFdAr6BZQK+AXkGvgF4BiwfQK6BX0CyxHETrFdAroFfQLKBXQK+gV0CvgMUD6BXQK2iWWA6i9QroFdAraBbQK6BX0CugV8DiAfQK6BU0SywH0XoF9AroFTQL6BXQK+gV0Ctg8QB6BfQKmiWWg2i9AnoF9AqaBfQK6BX0CugVsHgAvQJ6Bc0Sy0G0XgG9AnoFzQJ6BfQKegX0Clg8gF4BvYJmieUgWq+AXgG9gmYBvQJ6Bb0CegUsHkCvgF5Bs8RyEK1XQK+AXkGzgF4BvYJeAb0CFg+gV0CvoFliOYjWK6BXQK+gWUCvgF5Br4BeAYsH0CugV9AssRxE6xXQK6BX0CygV0CvoFdAr4DFA//H3v3AyFUfBh5/t93Ylus6tjFgShAuogSoAxts6jhgY1IfxxEHUc4JJHHCH0NiKOVf4IyxWW+S80F7EJLyxxhILMIRt4QQRGKIgoibQwjlgghHaGgbIQtZyEJIwEHOuMbpu/fsGTP79s3Om5n3ZufNfj7ST2nx7GOZ8ff3e/vb386iV0CvoFlKy4FovQJ6BfQKmgX0CugV9AroFTDxAHoF9Arjwp3zg+PuWTApvPvP/yC895QPxgdotxk9MUIHoq2xgF4BvYJmAb0CegW9AnoFTDyAXgG9Qs+7c15wZe3hWaP3hgPR1lhAr4BeQbOAXgG9gl4BvQImHkCvgF6hZ234aHCuQ8M9fyB6g7/p1lhAr4BeQbOAXgG9gl4BvQImHkCvgF6hJ22YFyyuHpx94IJTwg0DwWyjt8amxcEkf9OtsYBeAb2CZgG9AnoFvQJ6BUw8gF4BvUJPqj0QvXnl6ZoFayygV9AroFlAr6BXQK+AXgETD6BXQK9QHg5EgzUW0CvoVa+gWUCvoFe9gl4BvQImHkCvgF6htByIBmssoFfQq15Bs4BeQa96Bb0CegVMPIBeAb1CaTkQDdZYQK+gV72CZgG9gl71CnoF9AqYeAC9AnqF0nIgGqyxgF5Br3oFzQJ6Bb3qFfQK6BUw8QB6BfQKpeVANFhjAb2CXvUKmgX0CnrVK+gV0Ctg4gH0CugVSsuBaLDGAnoFveoVNAvoFfSqV9AroFfAxAPoFdArlJYD0WCNBfQKetUraBbQK+hVr6BXQK+AiQfQK6BXKC0HosEaC+gV9KpX0CygV9CrXkGvgF4BEw+gV0CvUFoORIM1FtAr6FWvoFlAr6BXvYJeAb0CJh5Ar4BeobQciAZrLKBX0KteQbOAXkGvegW9AnoFTDyAXgG9Qmk5EA3WWECvoFe9gmYBvYJe9Qp6BfQKmHgAvQJ6hdJyIBqssYBeQa96Bc0CegW96hX0CugVMPEAegX0CqXlQDRYYwG9gl71CpoF9Ap61SvoFdArYOIB9AroFUrLgWiwxgJ6Bb3qFTQL6BX0qlfQK6BXwMQD6BXQK5SWA9FgjQX0CnrVK2gW0CvoVa+gV0CvgIkH0CugVygtB6LBGgvoFfSqV9AsoFfQq15Br4BeARMPoFdAr1BaDkSDNRbQK+hVr6BZQK+gV72CXgG9AiYeQK+AXseFu+YFZ2ycG/zbxnnBe9HYEf3f24yeGKED0WCNBfQKetUraBbQK+hVr6BXQK+AiQfQK6DXnnf33ODe2sOzRu8NB6LBGgvoFfQKaBbQK+gV0CugV8DEA+gV0GvP2nhCMOTQcG+PH37tMs2CNRbQK+gV0CygV9AroFdAr4CJB9AroNfedPcJwfn7D8/OC4Y8I5oF9AroFfQKaBbQK+gV0CugV8DEA+gV9EppOBCtWUCvgF5Br4BmAb2CXgG9AnoFTDyAXkGvlJYD0ZoF9AroFfQKaBbQK+gV0CugV8DEA+gV9EppORCtWUCvgF5Br4BmAb2CXgG9AnoFTDyAXkGvlJYD0ZoF9AroFfQKaBbQK+gV0CugV8DEA+gV9EppORCtWUCvgF5Br4BmAb2CXgG9AnoFTDyAXkGvlJYD0ZoF9AroFfQKaBbQK+gV0CugV8DEA+gV9EppORCtWUCvgF5Br4BmAb2CXgG9AnoFTDyAXkGvlJYD0ZoF9AroFfQKaBbQK+gV0CugV8DEA+gV9EppORCtWUCvgF5Br4BmAb2CXgG9AnoFTDyAXkGvlJYD0ZoF9AroFfQKaBbQK+gV0CugV8DEA+gV9EppORCtWUCvgF5Br4BmAb2CXgG9AnoFTDyAXkGvlJYD0ZoF9AroFfQKaBbQK+gV0CugV8DEA+gV9EppORCtWUCvgF5Br4BmAb2CXgG9AnoFTDyAXkGvlJYD0ZoF9AroFfQKaBbQK+gV0CugV8DEA+gVxk2vP/mfd4WP33dnuGEgmG30xogPQTsQbY0F9AroFfQKaBbQK+gV0CugV8DEA+gVet4/XPrJcP/BWaM3hwPR1lhAr4BeQa+AZgG9gl4BvQJ6BUw8gF6hV91/zoADww5EY40F9Ap61SvoFdAs6FWvoFdAr6BXABMPoFcop3/4q6X7D87ePTd4M/rfbUbPjZP9TbfGAnoF9Ap6BTQL6BX0CugV0Ctg4gH0Cj3pB9ef752EwRoL6BX0qlfQK6BZ0KteQa+AXkGvACYeQK9QTg5EgzUW0CvoVa+gV0CzoFe9gl4BvYJe9QqYeAC9Qmk5EA3WWECvoFe9gl4BzYJe9Qp6BfQKetUrYOIB9Aql5UA0WGMBvYJe9Qp6BTQLetUr6BXQK+hVr4CJB9ArlJYD0WCNBfQKetUr6BXQLOhVr6BXQK+gV70CJh5Ar1BaDkSDNRbQK+hVr6BXQLOgV72CXgG9gl71Cph4AL1CaTkQDdZYQK+gV72CXgHNgl71CnoF9Ap61Stg4gH0CqXlQDRYYwG9gl71CnoFNAt61SvoFdAr6FWvgIkH0CuUlgPRYI0F9Ap61SvoFdAs6FWvoFdAr6BXvQImHkCvUFoORIM1FtAr6FWvoFdAs6BXvYJeAb2CXvUKmHgAvUJpORAN1lhAr6BXvYJeAc2CXvUKegX0CnrVK2DiAfQKpeVANFhjAb2CXvUKegU0C3rVK+gV0CvoVa+AiQfQ67hx94nBiXcMBCduGAhmG70xNq883YFosMYCegW96hX0CmgW9KpX0CugV9ArgIkH0Gvvu2tu8JP9B2eN3hwORIM1FtAr6BXQK6BZ0CugV0CvoFcAEw+g1161cW7wW4eGHYgGrLGAXkGvgF4BzYJeAb0CegW9Aph4QK+U0sYTgsdqDs++dPfcYKtR/nH/ZwbCvePcueGGecEcf9PBGgvoFfQK6BXQLOgV0CugV9ArgIkH9KrXnnTX3GBT9UD03ScE53tG9ApoFtAr6BXQK6BZ0CugV0CvoFcAEw/oldJwIFqvgGYBvYJeAb0CmgW9AnoF9Ap6BTDxgF4pLQei9QpoFtAr6BXQK6BZ0CugV0CvoFcAEw/oldJyIFqvgGYBvYJeAb0CmgW9AnoF9Ap6BTDxgF4pLQei9QpoFtAr6BXQK6BZ0CugV0CvoFcAEw/oldJyIFqvgGYBvYJeAb0CmgW9AnoF9Ap6BTDxgF4pLQei9QpoFtAr6BXQK6BZ0CugV0CvoFcAEw/oldJyIFqvgGYBvYJeAb0CmgW9AnoF9Ap6BTDxgF4pLQei9QpoFtAr6BXQK6BZ0CugV0CvoFcAEw/oldJyIFqvgGYBvYJeAb0CmgW9AnoF9Ap6BTDxwLjwyH+/MvzOfzo03PTJ2eHGecF344O0RvlH9TC0A9HWV0CzgF5Br4BeAc2CXgG9AnoFvQKYeKi44YbwsmiEKeNSz0553XvylLD28KzRe8OBaOsroFlAr6BXQK+AZkGvgF4BvdI5dc5YZRl7orErGm9F49loPBCNy9etC4/yrOoVMPGQ30L9fJ2F+DnPTnnde8p0h4Z7/0D0Un/Tra+AZgG9gl4BvQKaBb0CegX0Sme0cSC67hgcDH8e/e9cveoVMPHQ3iI9d7QFd2goHPAsldP9nz5u/8HZO+cFV26YFyw2emfc9dFgnr/l1ldAs4BeQa+AXgHNgl4BvQJ6pXOKOBBdHWvXhjfoVa+AiYfWF+mNDX4C6U7PUjnd/5mB/Qei4wO0nhGwvgKaBb0CegX0CpoF9AroFfQKrSvyQHTlrNZNegUw8dCkoaFwcrSQ7kwegE4stDujx03ybJWPA9FgfQU0C3rVK+gV0CtoVrOgV0CvoFe9kp+0Q8xZPzY+gxWNo9euDc8aHAxvjj72jTrvFH2WXgFMPDS3QH8psaC+Hi26/fH/Jv75lzxb5eNANFhfAc2CXvUKegX0CprVLOgV0CvoVa/kp50D0UmrV4cHDA6GT6Vcc9vQUNinVwATD9kX6GcT7w79d/E/j/73m4l//oxnq3wciAbrK6BZ0KteQa+AXkGzmgW9AnoFveqV/OR5IDp23XXh9OgaO5LXHBwMP6tXABMPGaxbFx6XskDPjf9saCgcSP5Z/HjPWrk4EA3WV0CzoFe9gl4BvYJmNQt6BfQKetUr+cn7QHTlmtekXHezXgFMPGQQvxt0YhF9MbHQvpD4qaNvetbKxYFosL4CmgW96hX0CugVNKtZ0CugV9CrXslPEQeih4bCY1Ou+5peAUw8NF5EJ0SL5u9qF9G1a8NVicX76sQi+3b8cZ698nAgGqyvgGZBr3oFvQJ6Bc1qFvQK6BX0qlfyU9CB6L6U6+7WK4CJhwYGB8MLahfQocFwT/hf/3zdXfOCL8YHZ+MRbvnUf1k3+O+/r31ceMeWv6n+udH9o3oY2oFosL4CmgW96hX0CugVNOvZAL0CegW9QvuKOBBd57o79Qpg4qGBwcHw6doF9G/++n/tqj08Wx3rV/5k2EL73y57Kkx7nNH9w4FosL4CmgW9AnoF9AqaBfQK6BX0Cu0p4kD09deHh6Rc9wW9Aph4GMXQUHhscgG98+wV/y/tEO2tZ35+xAJ+xylHO2DsQDRgfQXNahb0CugV9KpX0CygV9AroFfGnSIOREfXuDR5zcHB8Jt6BTDxMIposfxGYgHd9cSpE/9P9eDsXXOD70djUzz+79kT7vvq2l3v1T7+e1f8/YvVPze6e2xeeXoYjwevWhZuWhxM8rcfrK+AZkGvgF4BvYJmAb0CegW9QuvyPhB93XXh9OgarySvGb/ppV4BTDzUES2U/dGC+XpiAd1099xg6/53Eh4IZicW8XsSj389uk6fZ1OvgF5Bs5oFvQJ6Bb0CmgX0CnoF9Mp4kueB6DVrwkMHB8OnU655n15pU5gyABNP74gW0PNSFtCFDQ5EL0z5lQyf92zqFdAraFazoFdAr6BXQLOAXkGvgF4ZT9o5EB2/meW6deFRa9eGZw0OhrdHH7sz5Xq/iR43Va+0yYFoMPH0tmgh/XliAd0e//PRDkRXFvJtiY/b6tnUK6BX0KxmQa+AXkGvgGYBvYJeAb0ynqQdiM5xPLt6dXigXsmBA9Fg4uld69aFR6YsouvjP8twIPrryY+Nr+dZ1SugV9AsoFdAr6BXQLOAXkGvgF4ZLwo6CL1z7dpw3dBQ2KdXvebEgWgw8fSuwcHwppRDzUfFf9boQPRoh6nRK6BX0CygV0CvoFdAs4BeQa+AXhkPCjoQvTsaDwwNhcfqVa85cSAaTDy9Kf7poWjRfK12IR0cDJ+p/nmjA9Gx6PFPJxbiHeP5p5L0CugVNKtZ0CugV9AroFlAr6BXQK+MLwUdiK6OPfE7ReuVHDgQDY088IUF4b0nTwm/84kDw/gQrVGO8YPPrXgxuYBuPu/6f6n+efUw9GgHoqOP+VLyGtECfJYq3CgAegXNAnoF9Ap6BTQL6BX0CuiV8SDtIHPWj43ffDIak6OPWTg4GF4Q/e/D8SHolGtu1CttciAaGrn7z/8grD08a5RjrL/0yWGL5uDa3eGGj01PfWy9A9HRYjy18usZaq/1E1W4UQD0CpoF9AroFfQKaBbQK+gV0CvjQTsHotMMDYXHRtd4OXnN+MC0XmmDA9HQyN3zJzhgXLJxx8mHF/lrGsI1a8LDleFGAdAraBbQK6BX0CugWUCvoFdAr/S6vA9Ex4aGwiOi6+xKXPe16J9P0istciAaGvnOkoPefyfhecFio/vHP9/83HeLPBAdja8qw40CoFfQLKBXQK+gV0CzgF5Br4Be6XVFHIiODQ6Gd6a8S/QKvdIiB6Khke/8x1n7D0R7Nrrf0FDYFy2O2ws+EL3dM+1GAdAraBbQK6BX0CugWUCvoFdAr/S6og5Er10bLk259kN6pUWtHog+r87HxuNqTys9xYHocqmzUOY+on/PGZ5tNwqAXkGzgF4BvYJeAc0CegW9AnqllxV1IHpoKJyccu1X9UqLWjkQfWlQ/zD0Sk8pPceB6NItwI+lLJRz21x8B1Ku+WPPthsFQK+gWUCvgF5Br4BmAb2CXgG90suKOhBd59q79EqLmj0QvSaofxj6855OepID0eWxZk14WLQo7kkski/mtPi+mLjunujfd6hn3Y0CoFfQLKBXQK+gV0CzgF5Br4Be6VUdPhC9W6+0qJkD0TfVeXz89+9MT2Vk47zgf989N3hz49zg5eh/txq9MaqHoR2I7n5r14brkotk9M9W53Tt1SnXvsGz7kYB0CtoFtAroFfQK6BZQK+gV0Cv9KqiDkRff314cMq139IrLcp6IPr2Oo/dGY3TPI0VtQdnjd4c/pZ3/eL7SnKRzOtdnCvvPp1cgLd51t0oAHoFzQJ6BfQKegU0C+gV9ArolV5V1IHowcHwsynXfkyvtCjLgej76jwuPoh/kqewhgPDvT2+vXiGiaeLrV0bnpayQD6Z8+L+ZMq7RC/x7LtRAPQKmgX0CugV9ApoFtAr6BXQK72owAPRT6ecxVqjV1o02oHo/mg8VOcxr0fjRE9fQvXg7F1zgx0b5gWLjd4Yj337m2E8nnj470083b3wPpxcIKNF84I8/x3R9c5LWeAf8uy7UQD0CpoF9AroFfQKaBbQK+gV0Cu9qIgD0YOD4RdSrrtnzZrwcL3SonoHoidF48d1/vy1aBzrqUtR827C2zwbJh46Z/Xq8MB4QUwskLuGhsJJef57outNiK+bXIjjf79XQa+AXkGzgF4BvYJeAc0CegW9Anql1+R9ILpyGHp3ynU36ZU2pB14nhKNJ+v82fZoHO5pq8OBaBMPYyP+VQmdWiCj696X8qsaVnkV9AroFTQL6BXQK+gV0CygV9AroFd6TbsHooeGwv5168Ljoo9bGY3n0q4Xjdevvz48WK+0Ie3Q89N1/vm/RuOQUvxXbRgIZo/FcCDaxMOYLbovpxxSXlLEvyu+bsqC/LJXQa+AXkGzgF4BvYJeAc0CegW9Anql19Q5wJzn2D04GJ6qV9oUZhy7o3Fgaf6rag4mj9VwINrEQ4fEi2HKIvlqwYv89pR/5yleDb0CegXNAnoF9Ap6BTQL6BX0CuiVXlLwYehXo7FQr+QgbGKsKc1/lQPRmHjG1YL7QHKhHBwMbyr437k+ZXG+36uhV0CvoFlAr4BeQa+AZgG9gl4BvdJLCjoI/drateG6oaFwil71mpNmDkTvicZxpfivig8kj+k4IbjN3y0TD8VbvTo8IFoc9yQXzGihPLbIf298/bRf3RB/Pl4VvQJ6Bc0CegX0CnoFNAvoFfQK6JVe0ebB513ReDsaz0Xj4Wh8dXAwPHVoKOzTq15zFjY5fhONSZ42TDyAXgG9gmYBvQJ6Bb0CmgX0CnoF9ArotRvUO/j8cDROq/Nnf+dpw8QD6BXQK2gW0CugV9AroFlAr6BXQK+AXrtB2oHn+2r+/Bt1HnOqpw4TD6BXQK+gWUCvgF5Br4BmAb2CXgG9Anoda2mHnWtNiMZvUh7zajSme/ow8QB6BfQKmgX0CugV9ApoFtAr6BXQK6DXsdToQHRsTjT2pDzuQU8fJh5Ar4BeQbOAXgG9gl4BzQJ6Bb0CegX0OpayHIiOrarz2M96CjHxAHoF9AqaBfQK6BX0CmgW0CvoFdAroNexkvVAdOyplMe+EY3DPI2YeAC9AnoFzQJ6BfQKegU0C+gV9AroFdDrWGjmQHR88PntlMdv9TRi4gH0CugVNAvoFdAr6BXQLKBX0CugV0CvY6GZA9GxL9T5mKs9lZh4AL0CegXNAnoF9Ap6BTQL6BX0CugV0GunNXsgOvZQysfsisaxnk5MPIBeAb2CZgG9AnoFvQKaBfQKegX0Cui1k1o5EH1ANHakfNwL0ej3lGLiAfQK6BU0C+gV0CvoFdAsoFfQK6BXQK+d0sqB6NhpdT72bz2lmHhoxaRozI7Gx6KxOBrzojHF04JeQa+AZgG9gl4BvQKaBb0CegX0StNmRWNOsO8sVjxmB97xVq+9rdUD0bE763z8Qk8rJh6yiBfZK6OxNRpv1plQ4rej/1E0zo/GNE8ZegW9ApoF9Ap6BfQKaBb0CugV0CsjxIedT4/GPdF4KUg/i/VuNH4VjduCfYek0WsvaedAdPyGrv+a8vGvRGOqpxYTD/UcGY3N0XivziQUjrIg3xo4GI1eQa+AZgG9gl4BvQKaBb0CegX0Siw+CH1RNLYHzZ3Fikd8OHqZp1CvPaKdA9GxudHYk3KN+z21mHhIW3xvDOochJ4yZVZ4yCHzwsMPXxwedNCcvf9/nUnqzcoiDnoFvQKaBfQKegX0CmgW9AroFdDrePWxaPw6SDljNWHClHDGjCPDww47ee+YNm122N8/qd55rK3RmOXp1Ctg4qGxWZWFc/9C2tfXHx5zzLLwzDM3hVddtSO84YZwxIj/+RlnbNh7SDplIY5/vUO/pxa9gl4BzQJ6Bb0CegU0C3oF9ArodZyJ31Dy3aDmPFV8AHrhwrXhRRf9Mly9+t0RZ7HWrHkvXL78iXD+/CvDyZNnJs9i7YjGyZ5WvVKY+N3Y/4OnARNPuc2OxrbaBTQ+CP3lL/869RB0vREvxrNmDSQX4scDh6LRK+gV0CygV9AroFdAs6BXQK+AXsePoaDmDNWkSdPC0067de+B56xnsVatemfv4enEu0bHB6yXeHr1SmHNPhCND3g6MPGU05RovFRdNOMFNH5H6GYOQid/SmnBgmv2vrt0zUK8KXAoGr2CXgHNAnoFvQJ6BTQLegX0CnrVa++L3xl6/9mpww9fHF511Y6Wz2PF7yYdv7N0zTXficZiT7Neyc3CYOSbwE72tGDiKZ8fBjU/iRQvoK0uvrXj9NNvSx6Kvs5TjV5Br4BmAb2CXgG9ApoFvQJ6Bb3qtYd9LNj3Ls57z0wdc8yypt4Vut649to3w0MOmVd7Fmt7NGZ5uvVKbtYGww9FPxONGZ4WTDzlsTyoeWfovA5DV8eiReuSv67hQ55y9Ap6BTQLetUr6BXQK2hWs6BXQK+gV732oP5ovBTUvDN0Hoehaw9FH3TQnNrzWBs85XolVyuj8fuaxv4pGod6WjDxlGMB/m013jPO2JDrYejqiBf2mglik6cdvYJeAc2CXvUKegX0CprVLOgV0CvoVa896KKgck5q0qRp4VVX7cj9LNYll7wU9vX1157Hmudp1yu5WhaNf6tp7JVofNjTgomnu62sRjtr1kCuP41UO7785V8nF+E5nnq96hX0CmgW9KpX0CugV9CsZkGvgF5Br/SQ+M0ptweVM1KnnXZrIWex4rFgwTW1Z7G+76nXK7n7i2i8U9PZ64EfPsDE09WeqQb7mc/8sLAFOB5z566sXYRv9dTrVa+gV0CzoFe9gl4BvYJmNQt6BfQKeqWHnB5UzkfNmHFkYW9OGY+vfOX1ve9AXfn3vReNmZ5+vZK7+AD068H75x7jA9J/4WnBxNN9ZlcWw3DatNmFLsDxuPDCZ2oPRG8L9v1EFHrVK+gV0CzoFdAroFfQLKBXQK+gV3rBPUHlfNSiResKPYuV8gaVF3n69UohPhyNV2pa+7doLPO0YOLpLudWIz3xxMsKX4DjA9dTpsyqXYQ/5CXQq15Br4BmQa96Bb0CegXNejZAr4BeQa/0iJeCytmoiy76ZeHnsT7zmR/WnsXa5OnXK4U5NBr/VNPb76Ox0tOCiad7bKgGevbZmwtfgOPx4Q+fVbsIL/ES6FWvoFdAs6BXvYJeAb2CZj0boFdAr6BXesCsoHIuasKEKXvfPLLos1jXXvtm7Vmsl7wEeqVQM6LxTE1z8Vhb+4A10XjXMPIYEyZMCKvD85Fp7KmGef75T3XkQHTi1zTs9hroVa+GoVfDMDRrGHrVq2Ho1TAMvRqGZj0fhqFXwzD0ahh6NXpg7Kqei5ox48iOnMWKR3//pOpZrH/3GujV6Mj418Sh6IXVA9FDiT8wDGMMxl/91W87sgAvWrTO820YhmEYhmEYhmEYhmEYhmEYhmEYhmEYhmEYRs+Oww47uWMHoqdNm+05N4zOjq9F418q//fWoEb8DtE7DSOPMXHixLA6PB+Zxu+rkV5yyUsdWYAXLlxbOzG85zXQq14NQ6+GYWjWMPSqV8PQq2EYejUMzXo+DEOvhmHo1TD0avTA2P8O0Yce+rGOHYieOvVDteexvA56NYofzyQOSJ8eQN7+8R//MawOz0Ym91ejXL78iY4swB/96EW1E8FFXgK96hX0CmgW9KpX0CugV9CsZwP0CugV9EoP+FBQORcVH1Lu1IHovr7+6lmsHV4CvVK4vwuGH4b+lqcEE093+B/VMJcuvacjC/Cf/MmS2sngZC+BXvUKegU0C3rVK+gV0Cto1rMBegX0CnqlR7wTjb2HlFevfrfws1hXXLG99izWrzz9eqVQDkNj4uliS6txHn/8+YUvwPEiP3nyzNoJYaaXQK96Bb0CmgW96hX0CugVNOvZAL0CegW90iN+GVTORn3xi1sLP4919tmba89i3ebp1yuFcRgaE0+Xiw8kvxcHOmXKrHDNmvcKXYA/97nHayeElzz9etUr6BXQLOhVr6BXQK+gWc2CXgG9gl7pIbcGlfNRCxZcU/iB6D/7s3Nrz2Od6+nXK4VwGBoTT0k8UQ319NNvK3QB/tM/XVo7KXzdU69XvYJeAc2CXvUKegX0CprVLOgV0CvolR5yclA5HzV58sxw1ap3CjuLdcklL4X9/ZOqZ7HejcYUT79eyZ3D0Jh4SuSsaqzTps0OV69+t5AF+Pzznwr7+vqrk0L8rtRHeur1qlfQK6BZ0KteQa+AXkGzmgW9AnoFvdJjfhVUzmMtXLi2sAPRxx9/fu0hzXs87Xoldw5DY+Ipod8GBf6qhjVr3gtnzjy6dmK4zVOOXkGvgGZBr3oFvQJ6Bc1qFvQK6BX0qtcetDSonJOK30Dy4ot/lft5rC9+cWvyzSnneNr1Sq4chsbEU1KLaxfhZcu+n+sC/NGPXlQ7MbwZjZmecvQKegU0C3rVK+gV0CtoVrOgV0CvoFe99qitQeW81EEHzQm/8pXXczuLdcklL4XTps2uPY/1dU+3XsmVw9CYeErunqDmUPS55/4olwV4/vwrw8TksNxTjV5Br4BmAb2CXgG9ApoFvQJ6Bb3qtYcdHex748i9Z6YOPfRj4apV77R9Fuuv/3pb8jD0S9GY4unWK7lxGBoTTw+IF8attTEvWrQuXLPmvZYW33gBP+aYZcnD0H4aCb2CXgHNAnoFvQJ6BTQLegX0CnrV63iwJBrvBpWzUzNnHh1++cu/bvkwdPwGl5Mnz6w9i7UjGvM8zXolN/85cBgaE0/PiA9F/7I26kMOmRcuX/5EU4vvmWduCqdO/VDyMPSmaPR7itEr6BXQLKBX0CugV0CzoFdAr6BXvY4Ty6PxXlA5Q9XX1x8uWHBNeO21b2Y+i3XFFdvDj3xk+d6PDd4/ixW/+/SAp1ev5G5d4DA0Jp6eER+K/n4w/DDz3l/bsHjx18OLL/7ViHeNXr363fDCC58JFy5cu/cnmZIfG421gcPQ6BX0CmgW0CvoFdAroFnQK6BXQK/jT/xO0fEB5v3nqSZMmBIef/z54bJl3w+vumrHiEPQ8T+L35TymGOWhf39k5JnsV6KxhxPq14pzOmeAkw8vWV5ciGuHfGvX5g2bfbexbneY6Lx22ic7KlEr6BXQLOAXkGvgF4BzYJeAb0Ceh3HZkbj8aDOOav43Z/js1hTp34o+U7QyXFrsO8NL9ErYOKhyYX469HYPsoimzZ+FY3LAu8KjV5Br4BmAb2CXgG9ApoFvQJ6BfRKVfxu0T+KxrtB9rNY70RjczTmefr0Cph4aN/iYN/h6K3R2BaN92oW3G2VhfqaaBzpqUKvoFdAs4BeQa+AXgHNgl4BvQJ6pa5p0Tg/GvdE49fReD14/wD0jmDfG1LeFo1zA+8IrVfAxAPoFdAraBbQK6BX0CugWUCvoFdAr4BeARMPoFfQq15Bs4BeQa96Bb0CmgW96hX0CugV9Apg4gH0CnoFNAvoFfQK6BXQLOgV0CvoVa+gVwATD+gV0CugWdAroFdAr6BZQK+AXkGvgF4BEw+gV0CvoFlAr4BeQa+AZgG9gl4BvQJ6BbKbGo2wxTGW1641PRqXReOhaLwWjV3R2B2Nt6PxWDSujsYBXmp0O3pb8Q3Cli1bwg51uyQam6LxQjR2VpqN//e5aNwejQVeZnTa+Mb+Rz/6UVjgGnhipcfnE53+IhrfiMZxXmZ0m63bxBfjRd27Lqy0+WQ03kpc99lo3BON07zM6LRxr/H6esUVV4Qd/hrz7DburcE9cXH3xPac0G1Oe06Jb04V2ZY9J3TafKdhjiMLe07otlzd2nNCp+VYX+ux54Ruu7db+05otlzN2nOCklha4GSwNCj+pv6GyuTS6HrxDcMFXm50W1/8Takbb7yx6BuEw6PxdMbr/TgaB3u50Wl6rxdeeGE4ceLELNdrdg2Mv7B+JOPn+nA0DvRyo9vGzVa7LeDe9aRg3zeRs36uv4nGqV5udJquwPV1NPFa+lrgm1NotpvuiWP2nNBtMQeii2rLnhM67f5vIttzQrfl6taeEzot/4Foe07otnu7te+EZsvTrD0nKJk1BS7gRV57SjS2tnDdm7zk6DZd/E2pFStWFHlTf2zKF92NxqvRONRLjk6Hr4EDAwOtXDfLGhj/ZObzTV735cA3qNDtqB5//PGwoG4va+NzvtxLjk675mvMh4N83/kH3BO316w9J3RbwJ5TgffE9pzQaTm+iWzPCd2Wq1t7Tui0Nw5E23NCt93XrX0nNFuuZu05QQk9VOCNd1HX7gv2/VqmVq/9WS87uh0p/ubUokWLivpifEKwbwO7les+X+kerK/Fr4GbWrzuZi85uq3f7QknnBAW0O05OXxx/3kvOzod868xzwvy/UYXaLa9Zu05odsCuv3Zz34WFnRPbM8JnXbXN5GfsOcEPdGtPSd0Wp711Z4Tui1Xt/ad0Gy5mrXnBCW1IxHkESW4dtpPjTwajU8H779bQDypzI3GN6OxJ/HY+POa5KVHt8PFB6JnzJgRFtTtNUH6Znb8K9f6K4+J/3dhNB5MeexKLzs6LXwNPC5I/+nFuL/plcdMr/z/aT8FeZSXHd12rNvJ0Xg98bj4474djTODfe+8FdR0G38jK+1XOb0V7PuVxaDTRB8f//jHww58jXlYpUPfnEKz3XNPbM8J3RbQbZ3fSJZXW/ac0GnO4n3i6mjw0EtrPo9to3x9ac8J3RbUbRO9Zu3WnhM6Lc/6Ohp7Tui2u9bXKvtOaLaAc05N9tpMs/acoISmJkLcWdS1J06cmNfNdXwTsCvxea9v8DGnptworPDyo9vhtmzZEhY4JzyVuPbGBo9PvmPIVi89Oh25Bi5fvrzR+trMGnhP4nHPBfV/Lekh0dieePzfeunRbcfuXVcm/jz+hvGJGT6fVSlfjN/g5UenI9fXBptneX2NOdq7gYBmO39PbM8J3RbU7Qc+8IGwwLbsOaHTnGX8hvKSYPhhybmjPNaeE7otqNsmD4Bk6daeEzotz/o6GntO6La71tcgsO+EZgtptoUD0c2stfacoISWJkJ8rKhrz58/P6+b66+2OHncnPi4h7z86Ha4G2+8MSxwTtiZuPahDR5/RCc2H6BknQ5bAwcGBrLe2GdZA+OfNn478bhjG1z3lMTjX/HSo9vG3eZ07/po0PqvId2Y+NinvfzodOT6mmGNbfdrzMuD1n4FHGi2uHtie07otgPdFtCWPSd0mrMM31CO33XyjSDboUd7Tui2wG6bOACStVt7Tui0HOvraOw5odvuW1878bUxjMtmmzwQ3exaa88JSij56xhuLura55xzTl43168Ew39S48iMH3dk4r/1bS8/uh0u5deX5jkn7G7hi+3ax+/y0qPT99fAvr6+8IEHHsh6Y59lDVwYjHynnixeSHzcHC8/uh2925zuXZPfTO5r4nM6yhfj6LT+15jV9TXDGtvO15hHBiM30nxzCs2O/T2xPSd024FuC2jLnhM6zVmGbyg/U/M5PN/gcvac0G2B3TZxACRrt/ac0Gk51tfR7qHtOaHb7ltfh31tHNh3QrM3j0Gvray19pyghB5KhHh2Udf+2te+lsfN9XGJz/dRLyG6za/bRYsWhQXOCf+cuPYRDR5/SOLxL3vpGeedDlsDP/7xjzf7q18auazFL0KSP5V8qZcf3Y7ebZf899b+t+728qPT97/GbOHXq7XiF4l/7zOBb06h2bG+J7bnBB3qtoDP254TOs1Zg3vi5DeyBxpczp4Tui2w24xfwzbbbTvsOaHTzqyv9dhzQrfdub7ad0KzBTXbxPd0Wllr7TlBCe1IhHhkUddu4t3wRrMi8fmu9BKi2/y6nTFjRljgnJD8FTDfbvD42xOPX++lZ5x3OmwNvPrqq/M+rHVf4nP+dMaPOyfxcfd5+dHt6N12wX/rhMC7CaDTul9jduBA9OrEv/N3wchfo+abU2i28/fE9pygQ90W8Hnbc0KnORvlnvjoYN87XFX//XdmuJw9J3RbYLcZvoZtpdtW2XNCp51bX9PYc0K33bu+2ndCswU1m/F7Oq2utfacoGSmBum/tuiAaNwQjWcr/yz+6d1Xo7E5GktbufbEiROrE0+7105unC1JTF7fCPa9pX312vEX2vFPmXzey41ux/TasSnR2Jb4d9wfjZOC93/lWvy/8ys3EbWP2175PGA8dzpsDbzllltqb+zzWAMfHWWNHc2SwE80o9umuu2Ce9fPJv57H/JXAJ2+v/5V19fvfve7YQGdxr/me0/i33lZ5c98cwrNju09sT0ndNuhbgtoy54TOs1n/3a/Ub6hvDUYfsgqSz/2nNBtgd1mOADSSretsueETju3vibZc0K33b2+2ndCswU1m/FAdKtrrT0nKJmliRAfi8YF0Xgr5aa4dsSL8LHNXHv+/PnhqlWrwhyundw4iyeeSdHY2OC68Xghw+cNui3m2lWHVR4fNjF+E43DvfTodPga+Pjjj4c//elPw0996lNZOsqyBiZv5Ke3+AXMDn8F0O3o3XbBvetziX/Xl/wVQKfvf42Z8/paq7/yMbXXeKLmz31zCs2O7T2xPSd026FuC2rLnhM6zWf/dq8631D+dOK6N2S8nD0ndFtgtw0OgLTarT0ndNr962ste07otvvXV/tOaLagZjMciG53rbXnBCWyJhHjW02EG/800sKs1/7DP/zDMKdrJzfO4g2xp3P8vEG3xVy7VvzTUV/KcMMQ3yBcHrz/U1Uw3jsdtgZu2bIlnDNnTphjp79LPL4/439vfzDyV7CBbjvTbSvWBSN/OnmCvwLo9P2vMQvs9KbEx74RjUNr/tw3p9Ds2K6t9pzQbYe6LbAte07oNKd1KuUbynEvLwfDDydPzng5e07otsBuRzkA0k639pzQafevr/ac0G251lf7Tmi2oGYbHIjOa6215wQl8VDQ3E8vhCk30kd0+NrJjbNHWrz2YV5+dNvRa9caCPb9BOSeBteL/zz+VRhHetnR6cg18KSTTmr12vXWwN1B6xtitR+3y18BdNuxbpv1+ZTrf9rLj0478jXmgpSP++wo66lvTqHZzq+t9pzQbfnvie05odN89m/TvqF8aeJaq5r4vO05odsCux3lAEg73dpzQqfdv77ac0K35Vpf7Tuh2YKabXAgOq97YntOUBI7ElH+PBpfqEwitT+pEP/07ulB+q9q+HmWax9//PHh9ddfH+Zw7d11JpTXg30/UXJszfXjX7t2VuU6ycc/5uVHtx29dtWVLdzc7IzGOV56dJq+Bn7wgx8Mc1oD29kQS97kg26779417RtT3/bSo9P66+uKFSvCnDqN323g5cTjH8x5LQb3xO2vrfac0G2574ntOaHT1jsdIfEN5fjarwTD36l5Sov7Rvac0G3O3dY5ANJut/ac0Gn3r68xe07otjzrq30nNFtQsw3e0T2Pe2J7TtDjzkqJ+KQWbhRavXbaJPJUNA5scO2vp3zcXC8num2511bmhBVB+qbYgpqbnPgGZ0nli/XkY8/wUjLOOx2xBn7kIx8JH3nkkUa9Zl0D8/rm1G4vJ7odvdsxuHe9POV6WwO/thSdjrq+NrgnbqbT2xOPey0aB+S8FoN74vbXVntO0KFuC2jLnhO01+kIiX3iLyQ+/uYmPwd7TlBgt3W+r9Nut1nZc0KnY7e+xuw5QXnWV/tOUFCzo5xzymOttecE48TmRLy3N3Fj3+61k289vy0aUzN+3k8lPvYbXkp021avzVw7vpF/O/G41Q2uuzLx+PinxqZ4KRnHnQ5bA2fNmhVu2bIla69Z1sBdgV9fCh3ptsP3rutTvvh+2pqKTut/jVldXzOssVk6XZLS4NIM66lvTqHZzt8T23OCDnWbc1v2nKD9TkdI7BM/l/j4I5r899tzggK7rfN9nXa7zcKeEzod2/XVnhOUa3217wQFNTvKOad211p7TjCOnJGI97kmbuzbvfbOxJ+vaOLzPido4VfXwHjqtsUD0VmufUPiMS9kvPaPEx93pZeScdzpsDXw2muvbabXLGvg7xKP6cv4efcnPu53Xkp0O3q3Hbp3nZCyURCPn/jCG52O/jVmE/fEjTqNf7Xh9iD7rw32zSkY23tie07QoW5zbsueE7Tf6QjV9fXee+9Ne+fXZtlzggK7TfkadiCHbkdjzwnGfn215wTlW1/tO0FBzdb5nk4e98T2nGAcmZAId2eWG/uM35xqdO03En9+QJNfGNR+7NteSnTbVq/NXPvJxGO+lPHaSxMf95iXknHc6bA18NFHH22m1yxr4MuJx0zO+HlPTXzcq15KdDt6tx24d41/YvnpYORG98PBvm8og05H+RqziXviRp3eF4x814/Rvjnsm1MwtvfE9pygQ93m3JY9J2i/0xGq6+uyZcuS96gXtPDvt+cEBXab8jXsN3Poth57TtAd66s9Jyjf+mrfCQpqts73dPK4J7bnBONMbbi7s9zYN3H4Y7RrP9HmzXrmzxvGY7ctHojOcu3ku4Ac3uINjpt7xnOnw9bAnNfX2KOJxyzJeN1TEh/3qJcR3Y7ebcH3ricFI98dJB43e6nQabavMZtcY0e7dpjzAM0We09szwk61G3ObdlzggLWqer6OmPGjOTHtfLur/acoMBuU+6Jd+TQbRp7TtA966s9Jyjf+mrfCQpqts4ecR73xPacYBzpC4p7h+hG174/aO1XqzX9ecN47LbFA9FZrr2njRt8N/foNGUN/NnPfpbn+hpLvqPAWRk/77MTH3eflxLdjt5tgfeul6esufHaeZ6XCp1m/xqziXviRtf2zSko1z2xPSfoULc5t2XPCQpYp+K19Vvf+lbyfrTVd7Wy5wQFdpv4GvaUoJh3o7PnBN21vtpzgvKtr/adoKBmU76nk9c9sT0nGEcOS4T7QqMb+ya+OdXo2pcFrb2TQOzwxMe+4qVEt2312sy1dyYek/VXpzX966aghzsdtgbecsstzfSaZQ1ckXjMTRk/7/WJj7vcS4luR++2oHvXe4KRG9nxx5zoZUKnzX2N2cQ9caNOfXMKynVPbM8JOtRtzm3Zc4L2Ox0hXls/97nPJe9HL23x32/PCQrsNvE17E05dVvLnhN03/pqzwnKt77ad4KCmk35nk5e98T2nKCE3k4EeEjGj/tC0Pin8odd+wc/+EHWb041uvZA4s/vaeK/N7npttlfAXTbsWs/n3jMKRmvvSTxcS/6K8A47nTYGvjJT36ymcMfWdbAExOP+UXGz/vZxMed6q8Auh292wLuXTcFIzexn4zGgV5adNr815hNHIhu1KlvTqHZct0T23NCtx3qNue27Dmh0/Y7HSFeW4866qjk/ejRLX7e9pzQbYHdJr6GfTanbqvsOaHT7lxf7Tmh2/Ktr/ad0GxBzaZ8Tyeve2J7TlBCjyQCvCbjxz0TNP71ZsOufckll2T95lSWa79c8+d7KjcOjfRVJpjaa1/grwC67di1NyYesz7jtTcnPu7b/gowzjvdvwb29fWF9957b5b1tZk18I3E4+Y3uPb8xON/FzT3K55gXHab873rDcHIDeybvKTotPWvMavra4M1toivMX0zCs2O/T2xPSd024Fuc27LnhM6zafTYX76059We62ON9r83O05oduCuq1+/Rp3Gwz/td7tdmvPCZ12//qalT0ndNsd66t9JzRbQLOJA9GTcmzWnhOU0MpEgPEkcESDj1md+JjtQfom1LBr/9Ef/VH4ve99L8zp2tcEI38dxGENrp38dU5vVSZB0G1nrr0g8bj4BuSMBtf+dMoX6Kf4K8A473TYGnjwwQeHDz74YKP1tZk1MHlTvy2o/xOah1bWYDfz6LbJbnO8d02+o8DuaJzj5USn+ayvDQ5YFvE1pm9Oodmxvye254RuO9Btzm3Zc0Kn+XQ6zI033phs5KE2P3d7Tui2oG6rhz9y7taeEzotx/qalT0ndNsd66t9JzRbQLOJA9FLc2zWnhOU0ORo7EhE+Fo0Lo/G4TWPm1CZMB5JifacrNeePn16mNO14495OWWyjG8ejqqZAKdG4+xg5E+MhJWJE3SbuPaMGTPCgq4d25ry+EeDfT/FVb1pj/tdGI07Ux77lJcfnY5cA+MfOspxDRxIeXz8uV8ajemVxxxY+f9fS3nscV5+dNvRe9dfBE2+CwnoNPv6Gv+mow5/jembU2h27O+J7Tmh24K6/eM//uOwwLbsOaHTfPZv97v44ouTH7e+zc/dnhO6Lajb6uGPnLu154ROy7G+ZmXPCd12x/pq3wnNFtBs4kD06pzXWntOUEJpP5mQddw/htc+MRo7W7z2LwK/Wg3dphoaGgoL7PawIH0zO8t4I3EjBON5fS16DXykxWtv8rKj2/rdTpw4Mcy521Pa+HzTBlhfx/5rTF2i2e5o1p4Tui2g27vuuiss4J7YnhM6zXd93e8Tn/hESwe97DlB57utHv7IsVt7Tui0XOtrFrpEt2O/vlbZd0KzOTebOBC9Oedm7TlBSa1uIdofR6N/jK+9JBpvN3ntF4N97zIAuq1zo5DyU455dju/sug3c+34176c5CVHp8PXwMmTJzd77axrYHxT/2qT134h2PfTyqDbOm655ZYw5243Bb45hU577WtMXaLZ7rkntueEbgvYcyrgntieEzrNf33da86cOcmPX5LD523PCd0W0G318EeO3dpzQqflWl+z0CW6Hfv1tZZ9JzSb855TzYHopwto1p4TlNSZQbaNqF3RWNPMhdevXx/OnDkzLOLakSOD9LenTxv3RGOKlxrdNr5RiLstak6IHBGNn2fs9qlK56DThAceeCAcGBjIesPd7Bp4cBPra/zuPtO91Oi28Rqbc7fbAt+cQqeFfI1Z4PraiC7RbHfdE9tzQrcF7DnF3RbYlj0ndJrPPXGQ8sMLB+T0edtzQrcF7DnFI8du7Tmh0/Ktr43oEt2O/fqaZN8Jzea851Q5EP12Qc3ac4KSmhCN86LxUDReqUwueyqTxWPBvp/UOLjZi8YTzhNPPBFed911Yd7XrrEgGrdH49ng/V8vEf9v/Csjbo7G0V5edNv0jUIhc0KNhZWb9+cT3T5f+ecLvbzotHGvd9xxR1jgGhh3uLGm0z2V/32u8s/ne3nRbUtrbB73rnsC35xCp4Xcq1bX17/8y78MO/w1pi7RbHfeE9tzQrf57zkV3ZY9J3Ta5j1xf39/8t4071/Nbc8J3ea855Rjt/ac0Gl519d6dIlux359rce+E5rNd89pdwe+lrXnBONdymY3oFdAr6BZQK+AXkGvgGYBvYJeAb0CegVMPIBeQa96Bc0CegW9ejZAr4BmQa+AXgG9gl4BTDyAXkGvgGYBvYJeAb0CmgW9AnoFveoV9Apg4gG9AnoFNAt6BfQK6BU0C+gV0CvoFdArYOIB9AroFTQL6BXQK+gV0CygV9AroFdAr4CJB9Ar6BXQLKBX0CugV0CzoFdAr4BeQa8AJh7QK6BXQLOgV0CvgF5Bs4BeAb2CXgG9AiYeQK+AXkGzgF4BvYJeAc0CegW9AnoF9AqYeAC9gl71CpoF9Ap61SvoFdAs6FWvoFdAr6BXABMPoFfQK6BZQK+gV0CvgGZBr4BeAb2CXgFMPKBXQK+AZkGvgF4BvYJmAb0CegW9AnoFTDyAXgG9gmYBvQJ6Bb0CmgX0CnoF9AroFTDxAHoFvQKaBfQKegX0CmgW9AroFdAr6BXAxAN6BfQKaBb0CugV0CtoFtAroFfQK6BXwMRj4gG9AnoFzWoW9AroFfQKaBbQK+gV0CugV8DEA+gV0CtoFtAr6FWvoFdAs6BXvYJeAb2CXvUKmHgAvYJeAc0CegW9AnoFNAt6BfQK6BX0CmDiAb0CegU0C3oF9AroFTQL6BXQK+gV0Ctg4gH0CugVNAvoFdAr6BXQLKBX0CugV0CvgIkH0CvoFdAsoFfQK6BXQLOgV0CvgF5BrwAmHtAroFdAs6BXQK+AXkGzgF4BvYJeAb0CJh4TD+gV0CtoVrOgV0CvoFfPBmgW0CvoFdAroFfAxAPoFdAraBbQK6BX0CugWUCvoFdAr6BXvQImHkCvoFdAs4BeQa+AXgHNgl4BvQJ6Bb0CmHhAr4BeAc2CXgG9AnoFzQJ6BfQKegX0Cph4AL0CegXNAnoF9Ap6BTQL6BX0CugV0Ctg4gH0CnoFNAvoFfQK6BXQLOgV0CugV9ArgIkH9AroFdAs6BXQK6BX0CygV0CvoFdArwAmHtAroFfQrGZBr4BeQa96Bc0CegW96hX0CugVMPEAegX0CpoF9AroFfQKaBbQK+gV0CugV8DEA+gV9ApoFtAr6BXQK6BZ0CugV0CvoFcAEw/oFdAroFnQK6BXQK+gWUCvgF5Br4BeARMPoFdAr6BZQK+AXkGvgGYBvYJeAb0CegVMPIBeQa+AZgG9gl4BvQKaBb0CegX0CnoFMPGAXvUKegU0C3rVK+gV0CtoFtAroFfQK6BXABMP6BXQK6BZ0CugV9CrXkGzgF5Br3oFvQJ6BUw8gF4BvYJmAb0CegW9ApoF9Ap6BfQK6BUw8QB6Bb0CmgX0CnoF9ApoFvQK6BXQK+gVwMQDegX0CmgW9AroFdAraBbQK6BX0CugV8DEA+gV0CtoFtAroFfQK6BZQK+gV0CvgF4BEw+gV9AroFlAr6BXQK+AZkGvgF4BvYJeAUw8oFe9gl4BzYJe9Qp6BfQKmtUs6BXQK+gV0CuAiQf0CugV0CzoFdAroFfQLKBXQK+gV0CvgIkH0CugV9AsoFdAr6BXQLOAXkGvgF4BvQImHkCvoFdAs4BeQa+AXgHNgl4BvQJ6Bb0CmHhAr4BeAc2CXgG9AnoFzQJ6BfQKegX0Cph4AL0CegXNAnoF9Ap6BTQL6BX0CugV0Ctg4gH0CnoFNAvoFfQK6BXQLOgV0CugV9ArgIkH0CvoFdAs6FWvoFdAr6BZzYJeAb2CXvUKegUw8YBeAb0CmgW9AnoF9AqaBfQK6BX0CugVMPEAegX0CpoF9AroFfQKaBbQK+gV0CugV8DEA+gV9ApoFtAr6BXQK6BZ0CugV0CvoFcAEw/oFdAroFnQK6BXQK+gWUCvgF5Br4BeARMPoFdAr6BZQK+AXkGvgGYBvYJeAb0CegVMPIBeQa96Bc0CegW96hX0CmgW9AroFdAr6BXAxAPoFfQKaBbQK+gV0CugWdAroFfQq15BrwAmHtAroFdAs6BXQK+AXkGzgF4BvYJeAb0CJh5Ar4BeQbOAXgG9gl4BzQJ6Bb0CegX0Cph4AL2CXgHNAnoFvQJ6BTQLegX0CugV9Apg4gG9AnoFNAt6BfQK6BU0C+gV0CvoFdArYOIB9AroFTQL6BXQK+gV0CygV9AroFdAr4CJB9Ar6FWvoFlAr6BXvYJeAc2CXvUKegX0CnoFMPEAegW9ApoF9Ap6BfQKaBb0CugV0CvoFcDEA3oF9ApoFvQK6BXQK2gW0CugV9AroFfAxAPoFdAraBbQK6BX0CugWUCvoFdAr4BeARMPoFfQK6BZQK+gV0CvgGZBr4BeAb2CXgFMPKBXQK+AZkGvgF4BvYJmAb0CegW9AnoFTDwmHtAroFfQrGZBr4BeQa+AZgG9gl4BvQJ6BUw8gF4BvYJmAb2CXvUKegU0C3rVK+gV0CvoVa+AiQfQK+gV0CygV9AroFdAs6BXQK+AXkGvACYe0CugV0CzoFdAr4BeQbOAXgG9gl4BvQImHkCvgF5Bs4BeAb2CXgHNAnoFvQJ6BfQKmHgAvYJeAc0CegW9AnoFNAt6BfQK6BX0CmDiAb0CegU0C3oF9AroFTQL6BXQK+gV0Ctg4jHxgF4BvYJmNQt6BfQKetUraBbQK+gV0CugV8DEA+gV0CtoFtAroFfQK6BZQK+gV0CvoFe9AiYeQK+gV0CzgF5Br4BeAc2CXgG9AnoFvQKYeECvgF4BzYJeAb0CegXNAnoF9Ap6BfQKmHgAvQJ6Bc0CegX0CnoFNAvoFfQK6BX4/+3cQWtUZxvH4YdhAqWUwFBCkdJdcSESupGsRIQgXZZCcdGlmyLiF3BdKEVKF92IFMnKXZF8AXEpFJHgohREpISSjQsZQhAhPpIJ9TwzMc9x5jBzp9cFf0rfZNJT3/7u1SF6BRweQK+gV0CzgF5Br4BeAc2CXgG9AnoFvQI4PKBXQK+AZkGvgF4BvYJmAb0CegW9AnoFcHhAr4BeAc2CXgG9gl71CpoF9Ap61SvoFdAr4PAAegX0CpoF9AroFfQKaBbQK+gV0CugV8DhAfQKegU0C+gV9AroFdAs6BXQK6BX0CuAwwN6BfQKaBb0CugV0CtoFtAroFfQK6BXwOEB9AroFTQL6BXQK+gV0CygV9AroFdAr4DDA+gV9ApoFtAr6BXQK6BZ0CugV0CvoFcAhwf0qlfQK6BZ0KteQa+AXkGz/jRAr4BeQa+AXgEcHtAroFdAs6BXQK+gV72CZgG9gl71CnoF9Ao4PIBeAb2CZgG9AnoFvQKaBfQKegX0CugVcHgAvYJeAc0CegW9AnoFNAt6BfQK6BX0CuDwgF4BvQKaBb0CegX0CpoF9AroFfQK6BVweAC9AnoFzQJ6BfQKegU0C+gV9AroFdAr4PAAegW9ApoF9Ap6BfQKaBb0CugV0CvoFcDhAb3qFfQKaBb0qlfQK6BX0KxmQa+AXkGvgF4BHB7QK6BXQLOgV0CvgF5Bs4BeAb2CXgG9Ag4PoFdAr6BZQK+AXkGvgGYBvYJeAb0CegUcHkCvoFdAs4BeQa+AXgHNgl4BvQJ6Bb0CODygV0CvgGZBr4BeAb2CZgG9AnoFvQJ6BRweQK+AXkGzgF4BvYJeAc0CegW9AnoF9Ao4PIBeQa+AZgG9gl4BvQKaBb0CegX0CnoFcHgAvYJeAc0CegW9AnoFzWoW9AroFfSqV9ArgMMDegX0CmgW9AroFdAraBbQK6BX0CugV8DhAfQK6BU0C+gV0CvoFdAsoFfQK6BXQK+AwwPoFfQKaBbQK+gV0CugWdAroFdAr6BXWADn8n7Le5y3m/dq9NeHeb/krZ7Q59jK2x/N4QH0CugVNAvoFdAr6BXQLKBX0CugV9CrXgnm07x76b+Xgt+3P/JWTtBz3Ch+rsMD6BXQK2gW0CugV9AroFlAr6BXQK+gV70SyHI6+E3M+y32NM3+peh5PMfXE36mwwPoFdAraBbQK6BX0CugWUCvoFdAr6BXvRLIndTuJeTD3Q3+HJfydpMXogG9AnoFzQJ6BfQKegU0C+gV9AroFdArYa2m8ReCt/N+yBuMvmcw+vudCd97OuhzXM7bS5NfsHZ4AL0CegXNAnoF9Ap6BTQL6BX0CugV9KpXgridmi8DP8pbOeJ7T+X9U3z/z8Ge46O8X9P7f+O0wwPoFdAraBbQK6BX0CugWUCvoFdAr6BXvRJAL+9lar4MfOaYz1wovv95oOe4lPdX8blJv23a4QH0CugVNAvoFdAr6BXQLKBX0CugV9CrXgngfBr/rcw1torPnQ3wHA/S+IvPf+d9mbwQDegV0CtoFtAroFfQK6BZQK+gV0CvgF4J6Vpqvgh8s/JzN4vPXQ3wHOVLz7fzPjniaw4PoFdAr6BZQK+AXkGvgGYBvYJeAb2CXvVKABup+SLwd5Wfu1x8biPAcxx+z5N08BupJ33NC9GAXgG9gmYBvQJ6Bb0CmgX0CnoF9ArolUA2U/NF4PXKz60Xn9sM8Bxbed8f8TUvRAN6BfQKmgX0CugV9ApoFtAr6BXQK6BXAnqWmi8CDyo/t1x87t/gz+GFaECvgF5Bs4BeAb2CXgHNAnoFvQJ6BfRKQMPUfBG4X/m5fvG5YfDn8EI0oFdAr6BZQK+AXkGvgGYBvYJeAb0CemWa/1DmsX6/33gRuM1n3/3c0tJS6OdIxQvR8/7/xczMzMzMzMzMzMzMzMzMzMzMzMzMLMLm/kL0NC8Cv/u5Xq8X+jm8EG1mZmZmZmZmZmZmZmZmZmZmZmZmZvY/fiH67W94jvwcXog2MzMzMzMzMzMzMzMzMzMzMzMzMzP7oPdwW9mfwUp7x3y99nn20nTm/Rz7U/zzF8Y0/3EBegX0CpoF9AroFfQKaBbQK+gV0CugV7rWxQvRw+Lrvcpn6RefG0757zbv5/BCNKBXQK+gWUCvgF5Br4BmAb2CXgG9AnqlY128EP20+PrHlc+yXHxue8p/t3k/hxeiAb0CegXNAnoF9Ap6BTQL6BX0CugV0CsBbabmi8DrlZ+7UHxuM/hzeCEa0CugV9AsoFdAr6BXQLOAXkGvgF4BvRLQRmq+CPxN5ee+LT63Efw5vBAN6BXQK2gW0CugV9AroFlAr6BXQK+AXgnoSmq+CPxT5ed+LD53PfhzeCEa0CugV9AsoFdAr6BXQLOAXkGvgF4BvRLQudR8Efhh5ef+LD53MfhzeCEa0CugV9AsoFdAr6BXQLOAXkGvgF4BvRLUi9R8GXjtmO9fK75/mNcL/hxeiAb0CugVNAvoFdAr6BXQLKBX0CugV0CvBHUrNV8GfpZ36ojv/TzvefH9v5+A5/BCNKBXQK+gWUCvgF5Br4BmAb2CXgG9AnolqK/S+AvBO3lX8waj71kZ/f3OhO9dPQHP4YVoQK+AXkGzgF4BvYJeAc0CegW9AnoF9Epg99L4S8E1u1Pxs9u8bNzlc8zqGR0eQK+gV0CzgF5Br4BeAc2CXgG9AnoFvcKC+SJvO7V7CXkrb7niZ7d52bjL55jVMzo8jpcVyAAACUBJREFUgF5Br4BmAb2CXgG9ApoFvQJ6BfQKeoUF9Fne/VT3EvLb3+Q8qPy5bV827uo5ZvmMDg+gV9AroFlAr6BXQK+AZkGvgF4BvYJeYUGdz7uV9zhvN+/16K+PRv/7Wsuf96EvG8/6Obp4RocH0CvoFdAsoFfQK6BXQLOgV0CvgF5BrwAOD+gV0CugWdAroFdAr6BZQK+AXkGvgF4Bh8fhAb0CegXNahb0CugV9ApoFtAr6BXQK6BXwOEB9AroFTQL6BXQK+gV0CygV9AroFfQq14BhwfQK+gV0CygV9AroFdAs6BXQK+AXkGvAA4P6BXQK6BZ0CugV0CvoFlAr4BeQa+AXgGHB9AroFfQLKBXQK+gV0CzgF5Br4BeAb0CDg+gV9AroFlAr6BXQK+AZkGvgF4BvYJeARwe0CugV0CzoFdAr4BeQbOAXgG9gl4BvQI4PKBXQK+gWc2CXgG9gl71CpoF9Ap61SvoFdAr4PAAegX0CpoF9AroFfQKaBbQK+gV0CvoVa+AwwPoFfQKaBbQK+gV0CugWdAroFdAr6BXAIcH9AroFdAs6BXQK6BX0CygV0CvoFdAr4DDA+gV0CtoFtAroFfQK6BZQK+gV0CvgF4BhwfQK+gV0CygV9AroFdAs6BXQK+AXkGvAA4P6FWvoFdAs6BXfxqgV0CvoFlAr4BeQa+AXgEcHtAroFdAs6BXQK+gV72CZgG9gl71CnoF9Ao4PIBeAb2CZgG9AnoFvQKaBfQKegX0CugVcHgAvYJeAc0CegW9AnoFNAt6BfQK6BX0CuDwgF4BvQKaBb0CegX0CpoF9AroFfQK6BVweAC9AnoFzQJ6BfQKegU0C+gV9AroFdAr4PAAegW9ApoF9Ap6BfQKaBb0CugV0CvoFcDhAb3qFfQKaBb0qlfQK6BX0KxmQa+AXkGvgF4BHB7QK6BXQLOgV0CvgF5Bs4BeAb2CXgG9Ag4PoFdAr6BZQK+AXkGvgGYBvYJeAb0CegUcHkCvoFdAs4BeQa+AXgHNgl4BvQJ6Bb0CODygV0CvgGZBr4BeAb2CZgG9AnoFvQJ6BRweQK+AXkGzgF4BvYJeAc0CegW9AnoF9Ao4PIBeQa+AZgG9gl4BvQKaBb0CegX0CnoFcHgAvYJeAc2CXvUKegX0CprVLOgV0CvoVa+gVwCHB/QK6BXQLOgV0CugV9AsoFdAr6BXQK+AwwPoFdAraBbQK6BX0CugWUCvoFdAr4BeAYcH0CvoFdAsoFfQK6BXQLOgV0CvgF5BrwAOD+gV0CugWdAroFdAr6BZQK+AXkGvgF4BhwfQK6BX0CygV0CvoFdAs4BeQa+AXgG9Ag4PoFfQq15Bs4BeQa/+NECvgGZBr4BeAb2CXgEcHkCvoFdAs4BeQa+AXgHNgl4BvYJe9Qp6BXB4QK+AXgHNgl4BvQJ6Bc0CegX0CnoF9Ao4PIBeAb2CZgG9AnoFvQKaBfQKegX0CugVcHgAvYJeAc0CegW9AnoFNAt6BfQK6BX0CuDwgF4BvQKaBb0CegX0CpoF9AroFfQK6BVweAC9AnoFzQJ6BfQKegU0C+gV9AroFdAr4PAAegW96hU0C+gV9KpX0CugWdCrXkGvgF5BrwAOD6BX0CugWUCvoFdAr4BmQa+AXgG9gl4BHB7QK6BXQLOgV0CvgF5Bs4BeAb2CXgG9Ag4PoFdAr6BZQK+AXkGvgGYBvYJeAb0CegUcHkCvoFdAs4BeQa+AXgHNgl4BvQJ6Bb0CODygV0CvgGZBr4BeAb2CZgG9AnoFvQJ6BRwehwf0CugVNKtZ0CugV9AroFlAr6BXQK+AXgGHB9AroFfQLKBX0KteQa+AZkGvegW9AnoFveoVcHgAvYJeAc0CegW9AnoFNAt6BfQK6BX0CuDwgF4BvQKaBb0CegX0CpoF9AroFfQK6BVweAC9AnoFzQJ6BfQKegU0C+gV9AroFdAr4PAAegW9ApoF9Ap6BfQKaBb0CugV0CvoFcDhAb0CegU0C3oF9AroFTQL6BXQK+gV0Cvg8Dg8oFdAr6BZzYJeAb2CXv1pgGYBvYJeAb0CegUcHkCvgF5Bs4BeAb2CXgHNAnoFvQJ6Bb3qFXB4AL2CXgHNAnoFvQJ6BTQLegX0CugV9Arg8IBeAb0CmgW9AnoF9AqaBfQK6BX0CugVcHgAvQJ6Bc0CegX0CnoFNAvoFfQK6BXQK+DwAHoFvQKaBfQKegX0CmgW9AroFdAr6BXA4QG9AnoFNAt6BfQK6BU0C+gV0CvoFdArgMMDegX0CprVLOgV0CvoVa+gWUCvoFe9gl4BvQIOD6BXQK+gWUCvgF5Br4BmAb2CXgG9AnoFHB5Ar6BXQLOAXkGvgF4BzYJeAb0CegW9Ajg8oFdAr4BmQa+AXgG9gmYBvQJ6Bb0CegUcHkCvgF5Bs4BeAb2CXgHNAnoFvQJ6BfQKODyAXkGvgGYBvYJeAb0CmgW9AnoF9Ap6BXB4QK96Bb0CmgW96hX0CugVNAvoFdAr6BXQK4DDA3oF9ApoFvQK6BX0qlfQLKBX0KteQa+AXgGHB9AroFfQLKBXQK+gV0CzgF5Br4BeAb0CDg+gV9AroFlAr6BXQK+AZkGvgF4BvYJeARwe0CugV0CzoFdAr4BeQbOAXgG9gl4BvQIOD6BXQK+gWUCvgF5Br4BmAb2CXgG9AnoFHB5Ar6BXQLOAXkGvgF4BzYJeAb0CegW9Ajg8oFe9gl4BzYJe9Qp6BfQKmtUs6BXQK+gV0CuAwwN6BfQKaBb0CugV0CtoFtAroFfQK6BXwOEB9AroFTQL6BXQK+gV0CygV9AroFdAr4DDA+gV9ApoFtAr6BXQK6BZ0CugV0CvoFcAhwf0CugV0CzoFdAroFfQLKBXQK+gV0CvgMMD6BXQK2gW0CugV9AroFlAr6BXQK+AXgGHB9Ar6BXQLKBX0CugV0CzoFdAr4BeQa8ADg+gV9AroFnQq15Br4BeQbOaBb0CegW96hX0CuDwgF4BvQKaBb0CegX0CpoF9AroFfQK6BVweAC9AnoFzQJ6BfQKegU0C+gV9AroFdAr4PAAegW9ApoF9Ap6BfQKaBb0CugV0CvoFcDhAb0CegU0C3oF9AroFTQL6BXQK+gV0Cvg8AB6BfQKmgX0CugV9ApoFtAr6BXQK6BXuvMG54lo4Zc9zxEAAAAASUVORK5CYII=[/img][br]
Das Ergebnis: Rotationskörper konkret
Im Applet unten können Sie beliebige Funktionen eingeben, die Rotationsvolumina durch Zylinder annähern, die Integratoinsgrenzen und sich die sich ergebenden Körper in 3d anschauen. [br][br]Als Beispiel ist die Funktion f(x)=sin(x) eingegeben. Sie liegt in der x-y Ebene, die hier in etwas ungewohnter Darstellung horizontal liegt.[br][br]Lassen Sie sich einfach ein paar Funktionen einfallen und betrachten Sie das Ergebnis.[br][br]Sie können sich auch den Rotationskörper einblenden lassen, links wird dann das Volumen angezeigt. Damit lassen sich auch Übungsaufgaben kontrollieren
Weitergehende Aktivitäten
Wer Lust hat, kann sich das Buch zu "augmented reality" mit GeoGebra anschuen:[br][url=https://www.geogebra.org/m/u7c8t4tp]Augmented Reality mit GeoGebra[br][/url]