Activity 3 - Concreção 9983

In [i]Concreção 9983[/i], Sacilotto uses geometric transformations to compose non-convex hexagons in the shape of L's, combined with the use of vibrant colors, resulting in a visually striking piece — a true masterpiece, just like all of his compositions. Sacilotto always went far beyond the simple composition of geometric shapes and made use of an exclusive color palette. In this artwork, in my opinion, he stood out for the diversity of materials and methods employed.[br][br]
Exhibition [i]Sacilotto em Movimento[/i], Casa do Olhar Luiz Sacilotto, Santo André - SP, on June 22, 2024.[br]Source: The author.
Exhibition [i]Sacilotto em Movimento[/i], Casa do Olhar Luiz Sacilotto, Santo André - SP, on June 22, 2024.[br]Source: The author.
His works frequently feature strict geometric patterns and abstract shapes that interact dynamically, creating illusions of movement. He used lines, polygons, circles, and others, organized precisely, generating compositions that seem to shift positions as the viewer moves. This sense of movement is generated by the repetition and transformation of geometric shapes, which creates a direct connection with the idea of what we call Geometry of Motion. The Geometry of Motion, or Geometry of Transformations, focuses not on the study of plane figures and their properties, but on the movements that such figures can undergo in the plane, without altering their shape or properties. In this geometry, the focus is on isometric transformations: rotation, translation, and reflection.
[i]Concreção 9983[/i], 1999[br]Acrylic on canvas[br]70 × 70 cm[br]Private collection, São Paulo[br]Source: Sacilotto, 2021
The presence of the Geometry of Motion is a prominent feature in many of Sacilotto's works. In the specific case of [i]Concreção 9983[/i], we can observe the presence of rotations and translations.[br][br]In previous activities, we used the commands [i]Translate[/i], [i]Reflect[/i], and [i]Rotate[/i], embedding them in button programming to recreate Sacilotto's works. By clicking these buttons, we were able to follow step by step the construction of the reinterpretations. However, this process can be quite tedious and laborious when reproducing an artwork by this artist.[br][br]Sacilotto was meticulous in his calculations, carefully exploring mathematical and geometric properties to compose his works. We have already seen that he used symmetries, repetitions, and geometric transformations precisely to achieve the desired effect. Therefore, recreating some of his works using GeoGebraScript programming not only allows for a visual reinterpretation but also provides a deeper understanding of his creative processes. By using sequences in programming, we can automate transformations such as translations, rotations, and reflections, making it easier to replicate the geometric structures that Sacilotto employed with such precision.
[i]Concreção 9983[/i], 1999[br]Acrylic on canvas[br]70 × 70 cm[br]Private collection, São Paulo[br]Source: Sacilotto, 2021
By carefully analyzing each of the L-shaped forms present in the artwork, it is possible to observe that all of them are representations of an L shape, which we will refer to as the "original form," generated through the application of two isometric transformations: rotation and translation. After applying these transformations to the original form, the images are relocated on a grid, resulting in the composition containing 49 shapes arranged as shown in the artwork.
First steps to create the reinterpretation of the artwork.
We will begin the creation of a reinterpretation of the artwork [i]Concreção 9983[/i]. To do this, open a new browser window and access GeoGebra online via the link [url=https://www.geogebra.org/classic?lang=pt_PT]https://www.geogebra.org/classic[/url] .[br][br][list=1][*]First, configure your GeoGebra so that the Algebra Window, the Visualization Window, and the Visualization Window 2 are open, allowing for effective and simultaneous work between them.[/*][*]Add the points A (0,0), B (1,0), C (1, 1), D (-1,1), E (-1,-1), and F (0,1) in the Input field of the Algebra Window.[/*][*]Using the Polygon Toolbar Image button [icon]/images/ggb/toolbar/mode_polygon.png[/icon], create the non-convex hexagon that will represent the original form of the artwork [i]Concreção 9983[/i]. You may choose to remove the labels from points and segments.[/*][/list][br]The following image is a representation of the activity performed so far.
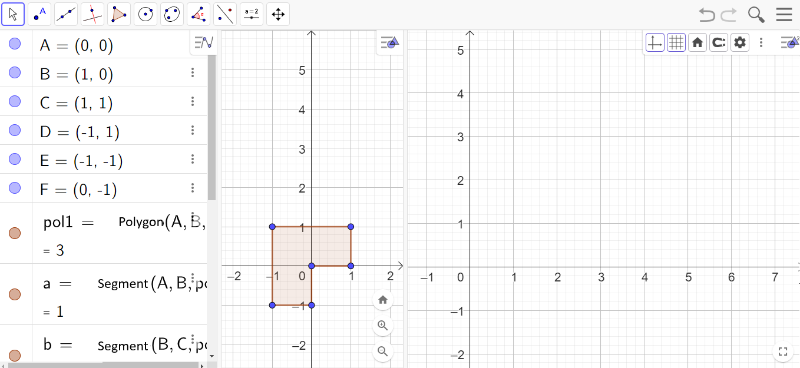
Source: The author.
Understanding the Sequence Command in GeoGebraScript.
We will create a grid of points that will be the image of point A, of the Polygon(A,B,C,D,E,F) – referred to as pol1 by GeoGebra – through an isometric transformation. For this, we will use the Sequence command in GeoGebraScript.[br][br]In GeoGebraScript, the Sequence command is used to generate a list of elements following a pattern defined by a mathematical expression. This command is very useful for creating sets of points, geometric objects, or figures based on a repeated formula. The basic structure of this command is:[br][br][code]Sequence(Expression, Variable, Initial Value, Final Value)[br][/code][br]Where:[br][br][list][*][b]Expression[/b]: The formula or object that will be generated at each step of the sequence.[/*][*][b]Variable[/b]: The variable used in the expression that controls the repetition.[/*][*][b]Initial Value[/b]: The initial value of the variable.[/*][*][b]Final Value[/b]: The final value of the variable.[/*][/list]
Question 1
When creating the points of a grid on the Cartesian plane, it is essential to define the ordered pairs that will represent these points. For the grid required to reinterpret [i]Concreção 9983[/i], taking the origin (0,0) as the first point of the grid, what would be the coordinates of the other points?
Question 2
When analyzing the ordered pairs presented in the previous question, identify which variable values the abscissas and ordinates of the points can assume.
Creating the grid of points using the Sequence command in GeoGebraScript.
To create a grid of points on the Cartesian plane using the Sequência command in GeoGebraScript, it is essential to properly define each component of the command. We need to establish the Expression, the Variable, the Initial Value, and the Final Value.[br][br]Let's start by defining the variable [b]i[/b], which will represent the values of the abscissas and ordinates of the points on the grid. In questions 01 and 02, we discussed these values, and each coordinate ranges from 0 to 6.[br][br]Since the grid should contain 49 points, distributed in 7 rows and 7 columns, the expression will be of the form (x(i), y(i)), where x and y depend on the variable i, which is related to the total number of points on the grid.[br][br]We define [b]n = 7[/b] as the number of points in each row or column, resulting in [b]n²[/b] points on the grid. The variable [b]i[/b] should range from [b]0 to 48[/b] (since we want to include the origin as one of the points and avoid points with ordinates equal to 7).[br][br]In fact:[br][list][*]By calculating the remainder of the division of [b]i[/b] by [b]n = 7[/b], we get values ranging from 0 to 6, which will represent the abscissas of the points on the grid.[/*][*]Similarly, by calculating the quotient of the division of [b]i[/b] by [b]n = 7[/b], the values will also range from 0 to 6, representing the ordinates of the points on the grid.[/*][/list][br]To create a grid with 49 points on the Cartesian plane, return to the previous construction and, in the Algebra input field, enter the Sequence command:[br][br][code]L = Sequence((Mod(i,7),Division(i/7)),i,0,48)[br][br][/code]
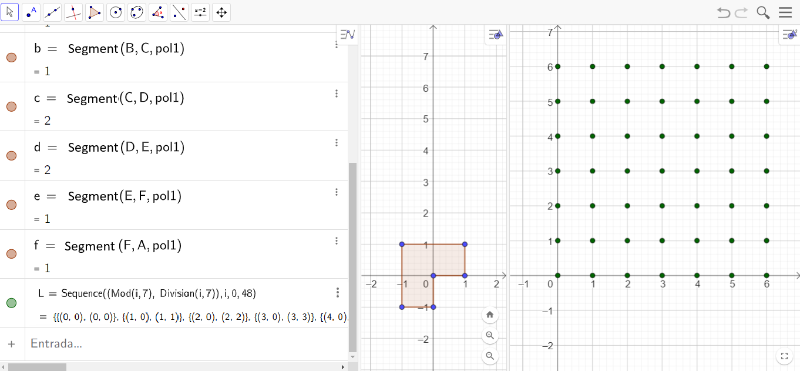
Source: The author.
If the point grid is visible in Viewing Window 1, you can modify its visibility by right-clicking on Sequence L. In the Settings menu, go to the Advanced tab, disable the Viewing Window option, and enable Viewing Window 2. Additionally, you can adjust the window sizes by dragging the edges and resizing them as needed.
Reinterpreting Sacilotto's work using the GeoGebraScript Sequence command.
After constructing the grid with 49 points, we will use isometric transformations to reinterpret [i]Concreção 9983[/i]. To do this, start by answering the questions that will help you understand the new [b]Sequence[/b] command that will be created.
Use the image below to answer the question.
Source: The author.
Question 3
Considering the original shape and the number of shapes arranged in this line, what is the rotation angle, relative to point P, that should be applied to the original shape to generate the subsequent shapes? And in which direction should this rotation occur?
Question 4
After rotating the original shape, which isometry should be applied to obtain the 7 shapes present in the line?
Let's start creating a Sequence command that reproduces the 49 shapes composing the artwork as a whole. Among these 49 shapes, one will be designated as the original shape, which, through the application of geometric transformations, will generate 48 additional images that, together with it, will form the complete artwork.[br][br]We will begin with the rotation of the original shape. It is important to remember that the [b]Rotate(Object, Angle, Point)[/b] command is used to rotate the desired object. Thus, we need to apply the command [b]Rotate(pol1, -15°, P)[/b] a total of 48 times.[br][br]However, each of the 48 shapes must be translated in a specific direction, determined by a vector, to each of the points in the grid mesh. Therefore, we must define a sequence that translates the original shape to obtain all the rotated polygons, positioning them at points in the grid mesh.[br][br]We will create another sequence, M, with the following characteristics:[br][br]M = Sequence(Expression, Variable, Initial Value, Final Value)[br][br]where i is the variable with an initial value of 1 and a final value of 49, since there will be 49 shapes in total.[br][br]In the expression, we must apply the translation after rotating the initial shape. The translation should consider the vector given by the direction L(i), where L represents the sequence of points in the grid.[br][br]Thus, we define:[br][br]M = Sequence([b]Translate(pol1, L(i))[/b], i, 1, 49)
Question 5
Return to the construction started in GeoGebra online and enter the following command in the Input field in the Algebra window:[br][br]M = Sequence[b](Translate(pol1, L(i))[/b], i, 1, 49)[br][br]What do you observe after entering this command? If desired, configure M to appear in Viewing Window 2.
Question 6
Did the command provide an opportunity for a reinterpretation of [i]Concreção 9983[/i]? Justify your answer.
With the previously described command, the shapes were translated but not rotated. Therefore, the command M = Sequence([b]Translate(pol1, L(i))[/b], i, 1, 49) needs to consider as the shape to be translated the one that represents the rotation of the original shape.[br][br]Instead of translating pol1, we will perform the translation of [b]Rotate(pol1, -15°, A)[/b], considering that point A, in the GeoGebra construction, corresponds to point P in the illustrative figure of the first row of Sacilotto’s artwork.
Question 7
Return to the construction started in GeoGebra online and enter the following command in the Input field in the Algebra window:[br][br]M = Sequence(Translate[b](Rotate(pol1, -15°, A)[/b], L(i)), i, 1, 49)[br][br]What do you observe after entering this command? If desired, configure M to appear in Viewing Window 2.
Question 8
Did the command provide an opportunity for a reinterpretation of [i]Concreção 9983[/i]? Justify your answer.
The rotation, in this reinterpretation, should not consider the original shape but rather the immediately preceding shape when following the row in which it is located. In the command:[br][br]M = Sequence(Translate[b](Rotate(pol1, -15°, A)[/b], L(i)), i, 1, 49) we will modify the [b]15° angle[/b] to [b](x(L(i)) + y(L(i))) · (-15°)[/b], where:[br][list][*][b]L(i):[/b] Refers to a specific point in the grid mesh, where [b]i[/b] identifies the point in the sequence.[/*][*][b]x(L(i)):[/b] Extracts the [b]x-coordinate[/b] of the point [b]L(i)[/b].[/*][*][b]y(L(i)):[/b] Extracts the [b]y-coordinate[/b] of the point [b]L(i)[/b].[/*][*][b]x(L(i)) + y(L(i)):[/b] This sum represents the combination of the [b]x and y coordinates[/b] of the point [b]L(i)[/b].[/*][*][b](-15°):[/b] This factor is an angle in degrees, used for rotation.[/*][/list]
Question 9
Return to the construction started in GeoGebra online and enter the following command in the Input field in the Algebra window:[br][br]M = Sequence(Translate[b](Rotate(pol1, (x(L(i)) + y(L(i))) * (-15°)[/b], A), L(i)), i, 1, 49)[br][br]What do you observe after entering this command? If desired, configure M to appear in Viewing Window 2.
Question 10
Did the command provide an opportunity for a reinterpretation of[i] Concreção 9983[/i]? Justify your answer.
Question 11
What geometric transformation can be applied to the original shape so that, after rotation and translation, the shapes arranged in the grid mesh represent a reinterpretation of the artwork?
To finalize the reinterpretation of Concreção 9983, we will apply a reduction of the original geometric shape using homothety. This should be done on the already rotated shape before it is translated.[br][br]The command [b]Dilatate(Object, Ratio, Center)[/b] should be used, considering the object we want to reduce—that is, the already rotated shape. The ratio must be a numerical value less than 1 to achieve the reduction, and the center of homothety will be point P of the original shape, which is represented in the GeoGebra construction as point A.[br][br]Applying a reduction to [b]Rotate(pol1, (x(L(i)) + y(L(i))) * (-15°), A)[/b], we can use the Dilatate command as follows:[br][br][b]Dilatate([/b]Rotate(pol1, (x(L(i)) + y(L(i))) * (-15°), A)[b], 0.5, A)[/b][br][br]After applying homothety, we can then translate the shape in the direction of the vector L(i).
Question 12
Write the sequence command that will perform the reduction, relative to the original shape, of the forms present in Luiz Sacilotto's artwork.
Return to the construction started in GeoGebra online and enter the following command in the Input field in the Algebra window:[br][br]M = Sequence(Translate(Dilate(Rotate(pol1, (x(L(i)) + y(L(i))) * (-15°), A), 0.35, A), L(i)), i, 1, 49)[br][br]This will complete the reinterpretation of Concreção 9983 according to its geometric composition.[br][br]You are invited to explore coloring the shapes so that the reinterpretation also includes the chromatic aspect of the artwork.
Question 13
Explore an interactive activity that simulates the creative process used by Sacilotto in his studio.[br]Adjust the sliders:[br][list][*][b]n[/b]: determines the number of shapes arranged in rows and columns.[/*][*][b]k[/b]: controls the degree of enlargement of each shape.[/*][/list]Experiment and compare your interpretation with the artwork [i]Concreção 9983.[/i][br]Are you able to identify the [b]values of n and k[/b] that allow for an accurate reproduction of the artwork?
Cerrar
– Cláudia Oliveira de Almeida Santos

Información: Activity 3 - Concreção 9983