Sistem persamaan linear dua variabel atau dalam matematika biasa disingkat [b]SPLDV [/b]adalah suatu persamaan matematika yang terdiri atas dua persamaan linear (PLDV), yang masing-masing bervariabel dua, misalnya variabel [i]x[/i] dan variabel [i]y[/i].[br][b][br]Ciri-Ciri SPLDV:[br][/b]1. [b]Hanya [/b]terdiri dari 2 variabel misal [i]x dan y, atau a dan b.[br][/i]2. Kedua variabel pada SPLDV hanya memiliki [b]derajat satu atau berpangkat satu[/b].[br]3. [b]Menggunakan[/b] relasi tanda sama dengan (=).[br]4. Tidak terdapat perkalian variabel dalam setiap persamaannya misal [b]xy[/b] atau [b]y/x.[/b]
Kita harus paham dulu unsur-unsur yang ada pada sistem persamaan linear 2 variabel. Apa saja sih memangnya?[br][br][b]1. Variabel, [/b]yaitu pengubah atau pengganti suatu bilangan yang belum diketahui nilainya secara jelas. Variabel biasanya disimbolkan dengan huruf, seperti [i]a, b,c, … x, y, z.[/i] [br][br][b]2. Koefisien[/b], yaitu bilangan yang menjelaskan banyaknya jumlah variabel yang sejenis. Koefisien terletak di depan variabel. Misalnya ada 2 lembar kertas dan 4 buah bolpoint, jika ditulis dalam persamaan yang mengandung variabel misalkan kertas = [i]x [/i], bolpoint = [i]y. [/i]Maka pernyataan 2 lembar kertas dan 4 buah bolpoint akan berubah menjadi [b]2x + 4y[/b][i].[/i][br][br][b]3. Konstanta[/b], yaitu nilai bilangan yang konstan karena bilangan tersebut tidak terkait (dikalikan) dengan variabel. Misal persamaan 2[i]x [/i]+ 5[i]y + [/i]7. Konstanta dari persamaan tersebut adalah 7, karena tidak ada variabel yang terkait oleh bilangan 7.[br][br][b]4. Suku[/b], yaitu bagian-bagian dari suatu bentuk persamaan yang terdiri dari koefisien, variabel, dan konstanta. Misal persamaan 12[i]x +y + [/i]4 = 2y, maka suku-suku dari persamaan tersebut adalah 12[i]x [/i], [i]y [/i], dan 4.
Metode ini menyelesaikan masalah dengan menentukan titik perpotongan dua garis lurus yang merupakan tampilan dari kedua persamaan linear dua variabel. [br][br]Berikut ini adalah langkah-langkah penyelesaian SPLDV dengan metode grafik: [br][br][b]1.[/b] Tentukan titik potong salah satu persamaan linear dengan sumbu X atau sumbu Y. [br][b]2.[/b] Hubungkan kedua titik potong dengan menggunakan garis lurus. [br][b]3.[/b] Lakukan langkah 1 dan 2 untuk persamaan lain pada SPLDV. [br][b]4.[/b] Jika kedua titik berpotongan di (x,y) = (x', y'), penyelesaian SPLD adalah x=x' dan y=y'. [br][b]5.[/b] Jika kedua titik tidak berpotongan, SPLDV tidak memiliki penyelesaian.
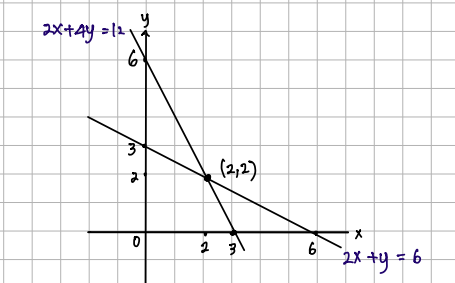
Dilansir dari laman https://mathdium.com/t/penyelesaian-spldv/185
[b]Diberikan dua buah garis g1 dan g2 dimana g1: y = mx + b bergantung pada dua parameter yaitu b,m dan g2: y = Mx + B bergantung pada dua parameter yaitu B,M. TiPot merupakan titik potong dari kedua garis g1 dan g2 yang secara aljabar merupakan solusi dari sistem persamaan linier dua variabel.[/b]
[b]Jawablah soal-soal latihan berikut[br][br][/b]1. Aturlah parameter-parameter tersebut sehingga g1 dan g2 tidak akan saling berpotongan. Tunjukan berapa nilai (B,M) dan (b,m) nya![br][br]2. Apakah mungkin g1 dan g2 berpotongan di lebih dari 1 titik? Jelaskan argumentasimu!
[1] Anissa. (2024, Agustus). Penyelesaian SPLDV. 22 Januari 2025, https://mathdium.com/t/penyelesaian-spldv/185[br][br][2] Daffa Dhiya. (2022, 22 Juli). Persamaan Linear Dua Variabel: Metode Eliminasi & Substitusi. 22 Januari 2025. https://www.zenius.net/blog/persamaan-linear-2-substitusi-eliminasi[br][br][3] Olivia, (2021, 26 Oktober). Persamaan Linear Dua Variabel: Metode Eliminasi & Substitusi. 22 Januari 2025. https://www.detik.com/edu/detikpedia/d-5782811/persamaan-linear-dua-variabel-metode-grafik-substitusi-dan-eliminasi

